Похожие презентации:
Теория вероятностей (ТВ)
1. Теория вероятностей (ТВ)
Изучает закономерностимассовых случайных явлений
2.
В современном мире автоматизации производстватеория вероятности(Т.В) необходима специалистам
для решения задач, связанных с выявлением
возможного хода процессов, на которые влияют
случайные факторы(например, ОТК: сколько
бракованных изделий будет изготовлено). Возникла
Т.В. в 17 веке в переписке Б. Паскаля и П.Ферма, где
они производили анализ азартных игр. Советские и
русские ученые также принимали участие в развитии
этого раздела математики: П.Л. Чебышев, А.А. Марков,
А.М. Ляпунов, А.Н. Колмогоров.
3. Под случайным событием понимается всякое явление, о котором имеет смысл говорить, что оно происходит или не происходит.
4. Основные понятия и термины ТВ
• Наблюдения, опыты и измерения• Испытание - осуществление
каждого отдельного наблюдения,
опыта или измерения
• Комплекс условий - совокупность
условий, при которых выполняется
каждое отдельное испытание
5. Основные понятия и термины ТВ
• Результат испытанияназывается событием
• Событие - любой факт, который может
произойти в результате испытания
• События обозначают начальными
заглавными буквами латинского
алфавита:
• А, В, С,… или А1, А2, А3, …
6. Основные понятия и термины ТВ
• Каждое событие обладаетобъективной возможностью
наступления
7.
Достоверным назовем событие котороеобязательно произойдет при выполнении
определенного количества условий
Невозможным назовем событие которое не
происходит при выполнении определенного
количества условий
Два события называются несовместными, если
появление одного из них исключает появление
другого. В противном случае события называются
совместными.
8.
Примеры:1) При подбрасывании монеты появление цифры
исключает одновременное появление герба:
А появление
В появление
гербаГ ,
решкиР ,
несовместные
события.
2) Есть билет лотереи «Русское лото»:
А билет
В билет
выиграшный,
невыигрышный,
несовместные
события.
9. Основные понятия и термины ТВ
• В любом опыте имеется определенноемножество возможных исходов ωi, (i =
1, 2,…n) называемых элементарными
исходами или элементарными
событиями
• Все возможные исходы опыта
образуют пространство Ω
элементарных событий
(элеметарных исходов) этого
опыта
10. Основные понятия и термины ТВ
• Например,1 1 , 2 Г, Ц
• - пространство элем. исходов опыта,
связанного с подбрасыванием одной
монеты;
2 1 , 2 , 3 , 4 ГГ, ГЦ, ЦГ, ЦЦ
• - пространство элем. исходов опыта,
связанного с подбрасыванием двух
монет
11. Основные понятия и термины ТВ
• СобытиеA выпадение "герба" 1 Г
• - подпространство пространства 1
• Событие
B хотя бы один "герб" 1 , 2 , 3 ГГ, ГЦ, ЦГ
• - подпространство пространства 2
12.
Оказывается, что при многократном повторении опытачастота события принимает значения, близкие к некоторому
постоянному числу. Например, при многократном бросании
игральной кости частота выпадения каждого из чисел очков
от 1 до 6 колеблется около числа 1
6
Многократно проводились опыты бросания однородной
монеты, в которых подсчитывали число появления «герба», и
каждый раз, когда число опытов достаточно велико, частота
1
события «выпадения герба» незначительно отличалась от 2
для наглядности рассмотрим таблицу результатов,
полученных в 18 веке французским естествоиспытателем
Жоржем Луи Леклерк Бюффоном(1707 – 1788) и в начале 20
века – английским статистиком Карлом Пирсоном(1857 –
1936).
13.
Числобросаний
Число
выпадений
герба
Частота
Ж. Бюффон
4040
2048
0,5080
К. Пирсон
12000
6014
0,5016
К. Пирсон
24000
12012
0,5006
Экспериментатор
14. Виды событий в ТВ
• В зависимости от объективнойвозможности наступления:
• 1. Достоверное
А U
• 2. Невозможное
• 2. Случайное
A V
A,B,C,... или
A1 ,A2 ,...,An
15. Виды случайных событий
• 1. Простое - не может быть разложенона составляющие.
• Например:
• Событие A Г - при бросании
монеты;
• Событие B 2 - при бросании
игральной кости;
• Событие C 0 - при измерениях
( - случайная ошибка измерений)
16. Виды случайных событий
• 2. Сложное (составное) событие описывается несколькими простымисобытиями.
• Например: событие
C нечетная цифра 1,3,5
- при бросании игральной кости
17. Виды сложных событий
• а) Логическая сумма (объединение)простых событий – сложное событие,
которое заключается в наступлении
хотя бы одного из нескольких событий.
• Например:
S1 = четная цифра 2 ,4 ,6
• 1)
• 2)
появление хотябыодной
S 2 положительной случайной
ошибки при двух измерениях
18. Виды сложных событий
• Общепринятая запись суммы(объединения) двух событий:
S A1
A2
или
S А1 А2
• что означает:
S = или А1 ,или А2 ,или А1 и А2
- символ логического сложения.
19. Виды сложных событий
• Сумма (объединение) трех событий:• S A1 A2 À3
• что означает:
или
S А1 А2 А3 ,
èëè À1 ,èëè À2 ,èëè À3 ,èëè À1èÀ2 ,
S =
èëè À1èÀ3 ,èëè À2èÀ3 ,èëè À1èÀ2èÀ3
20. Виды сложных событий
• б) Логическое произведение(пересечение) простых событий сложное событие, которое
заключается в совместном
наступлении одновременно или
последовательно друг за другом
нескольких событий.
21. Виды сложных событий
• Например, событиеП 1 выпадение цифры6 на обеих костях
• - при бросании двух игральных костей.
• Или событие
появление двух положительных
П 2 случайных ошибок
при двух измерениях
22. Виды сложных событий
• Общепринятая запись произведения(пересечения):
• Ï A1 A2 À3 или П A1 A2 А3 ,
• что означает:
П иА1 ,иА2 ,иА3 ;
- символ логического
умножения.
23. Виды случайных событий (продолжение)
• 3. Равновозможные события – имеютодинаковую объективную возможность
наступления при данном комплексе
условий.
• Например, события:
A Г
равновозможны
B Ц
при бросании монеты
24. Виды случайных событий
• СобытияА1 1
А2 2
равновозможны
...............
А6 6
при бросании игральной кости ;
25. Виды случайных событий
• События• C 0 и
D 0 ,
• где - случ. ошибка измерений, равновозможны при однократном
измерении некоторой величины.
26. Виды случайных событий
• 4. Единственно возможные события –такие, когда в результате испытания
может произойти одно и только одно из
этих событий
• Так, в предыдущих примерах события Аi
единственно возможны, равно как и
события С и D
• Система единственно возможных
событий данного опыта образует
пространство Ω элементарных
событий этого опыта
27. Виды случайных событий
• 5. Независимые и зависимые события– такие, у которых объективная
возможность появления не зависит или
зависит от того, появилось или нет
другое событие.
28. Виды случайных событий
• Система единственно возможныхнесовместных событий называется
полной группой событий.
• Так события
• А Г и В Ц при одном бросании
монеты составляют полную группу
событий,
• равно как и события А ,А ,...,А
1
2
• при бросании игральной кости.
6
29. Виды случайных событий
• 6. Противоположные события – двапростых или сложных события,
образующих полную группу.
• Событие, противоположное событию А
обозначается А
30. Виды случайных событий
• Так, противоположны события:• А Г
и
А Ц
А 2, 4, 6
А 3
и
и
;
А 1, 3, 5 ;
А 1, 2, 4, 5, 6
31.
• Конечное число несовместныхравновозможных событий, образующих
полную группу, называются случаями,
шансами, элементарными исходами
опыта.
• Например, при бросании монеты
возможны только два элементарных
исхода: Г - “герб” и Ц - “цифра”, а при
бросании игральной кости – шесть, а
именно: 1, 2, 3, 4 , 5, 6.
32.
• Про опыт говорят, что он сводится илине сводится к схеме случаев (шансов,
элементарных исходов).
• Элементарный исход называется
благоприятствующим данному
событию, если его осуществление
влечет за собой наступление этого
события.
33.
• Например, в опыте1 1 , 2 Г, Ц
• выпадению герба благоприятствует
один исход (Г);
• В опыте
2 1 , 2 , 3 , 4 ГГ, ГЦ, ЦГ, ЦЦ
• выпадению хотя бы одного герба
благоприятствуют три исхода
(ГГ,ГЦ,ЦГ)
34.
• Численная мера объективнойвозможности появления события
называется вероятностью события.
• Вероятность – важнейшая
характеристика случайного события.
• Существует несколько определений
вероятности, мы рассмотрим два из
них: классическое и статистическое.
35. Классическое определение вероятности
• Оно не связано с проведением опытов,т.е. вероятность события определяется
исходя лишь из условий опыта.
• Но при этом необходимо, чтобы
возможные исходы опыта составляли
схему случаев, т.е. были бы все
равновозможны, несовместны,
образовывали полную группу и их число
должно быть конечным.
36. Классическое определение вероятности
• Тогда вероятность события может бытьполучена по формуле
M
P
N
I
• где N – общее число возможных
элементарных исходов опыта;
• M – число исходов опыта,
благоприятствующих наступлению
интересующего нас события.
37. Классическое определение вероятности
• Согласно формулы ( I ),• При одном бросании монеты:
• Р(Г) = 1/2.
• При одном бросании игральной кости:
• P(6) = 1/6;
• Р{четная цифра} = 3/6 = 1/2.
38. Классическое определение вероятности
• В формуле (I) M N• или 0 M N ,
• т.е.
0 P 1
• Т.о. предельное числовое значение
вероятности вообще есть единица.
39. Классическое определение вероятности
• При M N имеем P() 1
• - вероятность достоверного
события равна единице.
• При M 0
имеем P(V ) 0
• - вероятность невозможного события
равна нулю.
• При 0 M N имеем 0 P 1
• - вероятность случайного события
может изменяться в пределах от нуля
до единицы, не достигая их.
40. Классическое определение вероятности
• Обозначим P( A ) p и , P( A ) q• Тогда
p q 1 , т.к.
M N M
1
N
N
,
• т.е. сумма вероятностей
противоположных событий равна
единице.
41. Классическое определение вероятности
• Недостаток: опыты редко сводятся ксхеме случаев и чаще всего
нарушается требование
равновозможности исходов.
• Поэтому формула ( I ) имеет
ограниченное (но достаточно широкое )
применение.
42. Статистическое определение вероятности
• Связано с проведением опытов и спонятием относительной частоты Q
– частости- появления интересующего
нас события в опытах:
k ,
Q
n
• где n – число испытаний;
• k – число появлений события в этих
испытаниях (абсолютная частота).
43. Статистическое определение вероятности
• Свойство устойчивости относительнойчастоты в опытах отражено в теореме
Бернулли:
k
P p 1
n
• где ε и δ - бесконечно малые числа.
• Или
k
lim
n
p
n
44. Статистическое определение вероятности
• На основании теоремы Бернулли :вероятность – это предел, к
которому стремится относительная
частота Q события при
неограниченном увеличении числа
испытаний.
45. Статистическое определение вероятности
• Практически статистическаявероятность может быть найдена по
приближенной формуле
k
P
n
(II)
46. Статистическое определение вероятности
• Недостаток - необходимостьвыполнения бесконечного числа опытов
или достаточно большого их числа, что
не всегда возможно, а чаще вообще
невозможно.
47.
• Формулы ( I ) и ( II ) выражают прямыеспособы определения вероятностей
случайных событий.
• Они являются главными, но не
основными.
• Основными следует считать косвенные
способы.
48. Косвенные способы вычисления вероятностей
• Позволяют по известным вероятностямодних событий вычислять вероятности
других, с ними связанных.
• Это сводит необходимый эксперимент к
минимуму.
• Вся ТВ есть система таких косвенных
способов.
49. Косвенные способы вычисления вероятностей
К ним относятся:
- теоремы (аксиомы) ТВ;
- формула полной вероятности;
- формула Байеса;
- формула Бернулли;
- формула использования вероятности
противоположного события и др.
50.
Задачи по теме:«Вероятность.
Понятие события и
вероятности события»
51.
1. В урне 3 белых и 9 черных шаров. Из урны наугадвынимается 1 шар. Какова вероятность того, что вынутый
шар окажется белым?
Решение:
Количество всех возможных результатов n=3+9=12.
Опытов, в результате которых может быть вынут
белый шар m=3.
m 3 1
P( А) 1.
n 12 4
Ответ:
0, 25
52.
2. Брошена игральная кость. Какова вероятность событий:А- выпало 1 очко; В- выпало 2 очка?
Решение:
Количество всех возможных результатов n=6 (все грани).
а) Количество граней, на которых всего 1 очко m=1:
1
P ( A) 1,
6
б) количество граней, на которых всего 2 очка m=1:
1
Ответ:
6
и
1
6
1
P ( В ) 1.
6
53.
3. Брошены 2 игральные кости. Какова вероятность событий: Авыпадения в сумме не менее 9 очков; В- выпадения 1 очка покрайней мере на одной кости?
Решение:
I
II
1
2
3
4
5
6
1
2
3
4
5
6
Получили, что возможно n=36 результатов испытаний
54.
Для события А получаем:I
II
1
2
3
4
1
2
3
4
5
6
m=10:
10 5
P( A)
1,
36 18
5
6
55.
Для события В получаем:I
II
1
2
3
4
1
2
3
4
5
6
m=11:
Ответ:
5
11
;
.
18
36
11
P( В)
1.
36
5
6
56. Основные теоремы ТВ
• Используются для вычислениявероятностей сложных событий.
• Их две – теорема сложения
вероятностей и теорема умножения
вероятностей.
• Строго могут быть доказаны только для
событий, сводящихся к схеме случаев.
• Для других событий применяются как
аксиомы, принципы, постулаты.
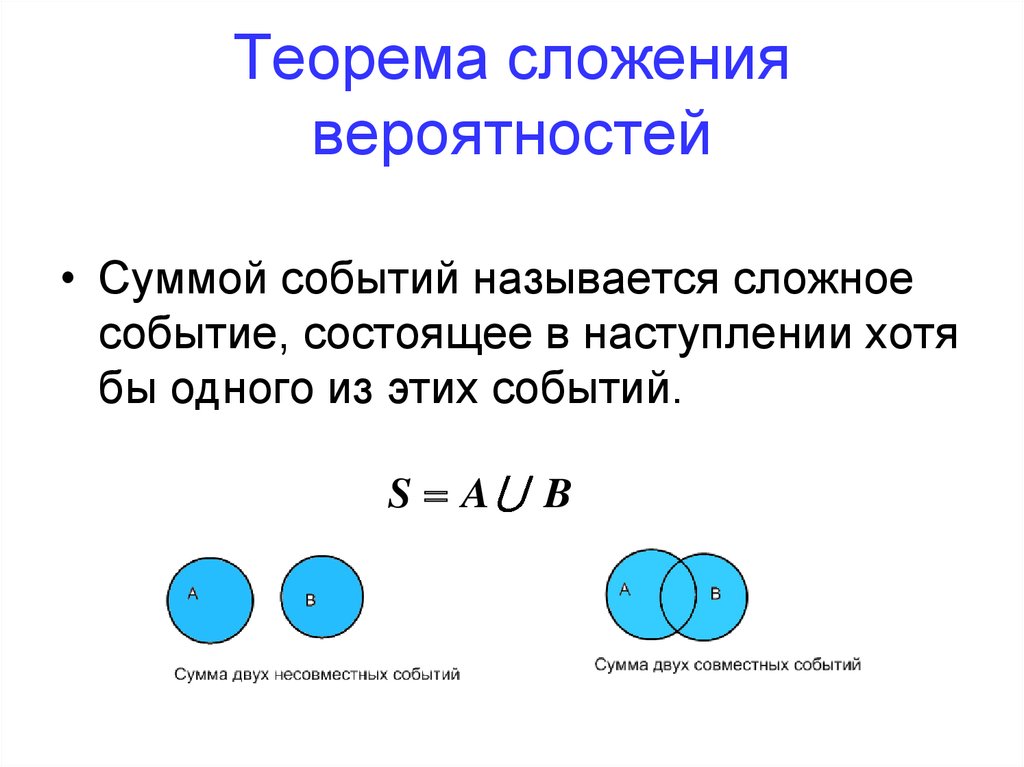
57. Теорема сложения вероятностей
• Суммой событий называется сложноесобытие, состоящее в наступлении хотя
бы одного из этих событий.
S A
B
58. Теорема сложения вероятностей
• Теорема: Вероятность суммы двухили нескольких совместных событий
равна сумме вероятностей этих
событий без вероятности их
совместного появления, т.е.
P( A
B ) P( A ) P( B ) P( AB )
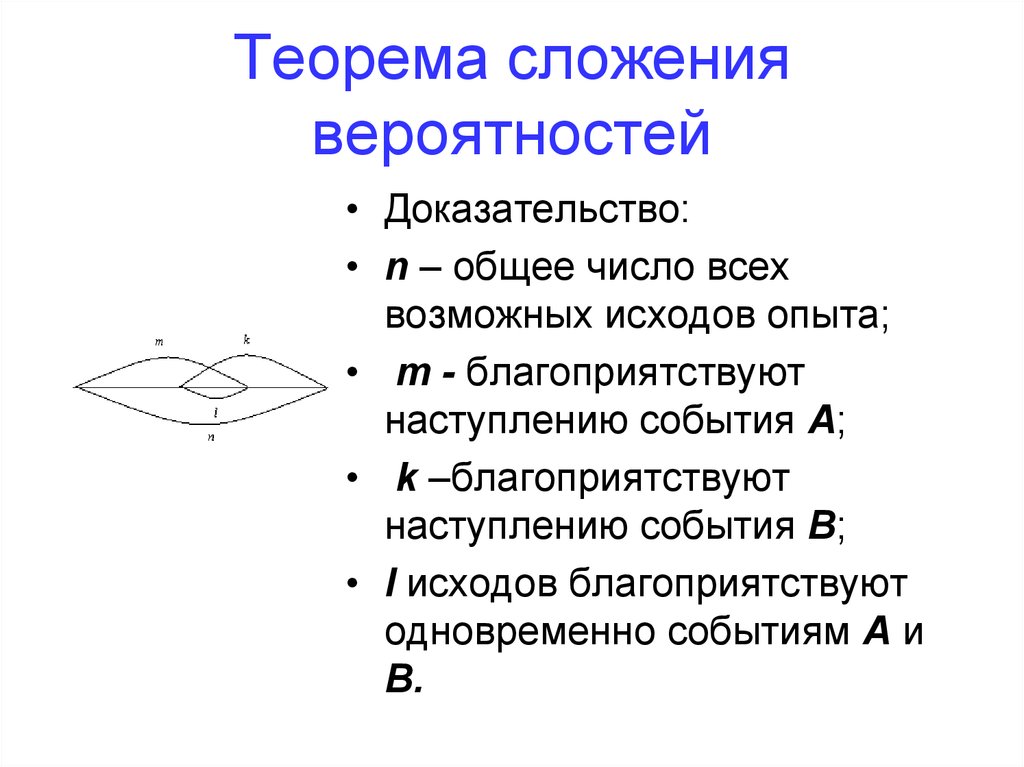
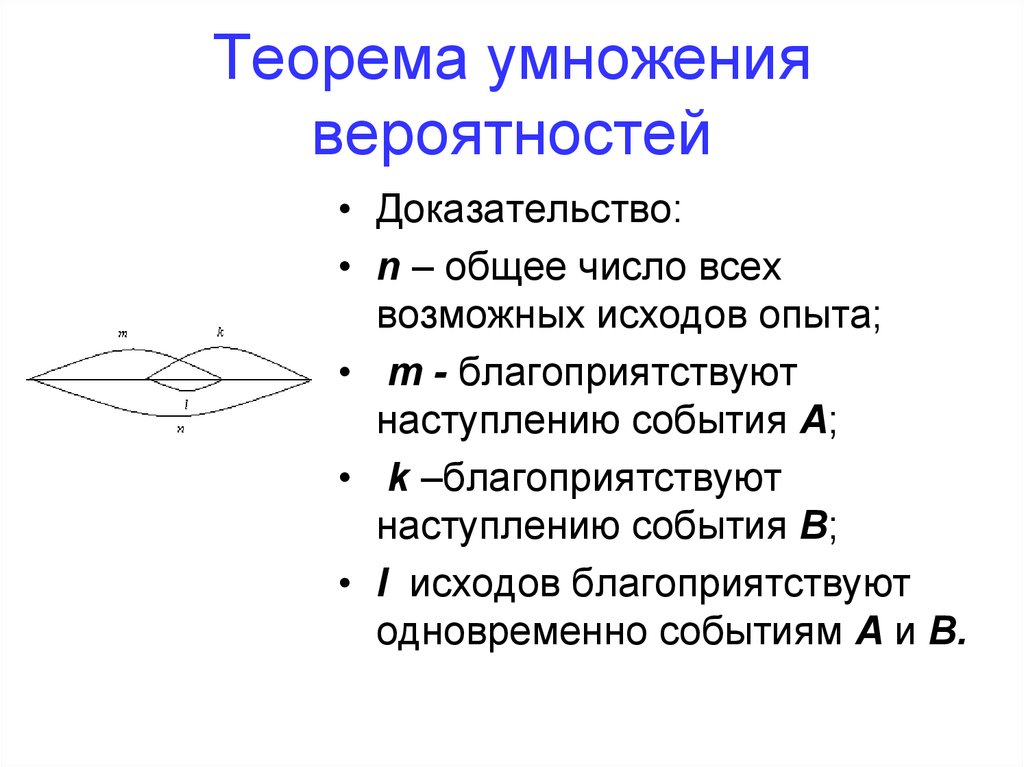
59. Теорема сложения вероятностей
• Доказательство:• n – общее число всех
возможных исходов опыта;
• m - благоприятствуют
наступлению события А;
• k –благоприятствуют
наступлению cобытия В;
• l исходов благоприятствуют
одновременно событиям А и
В.
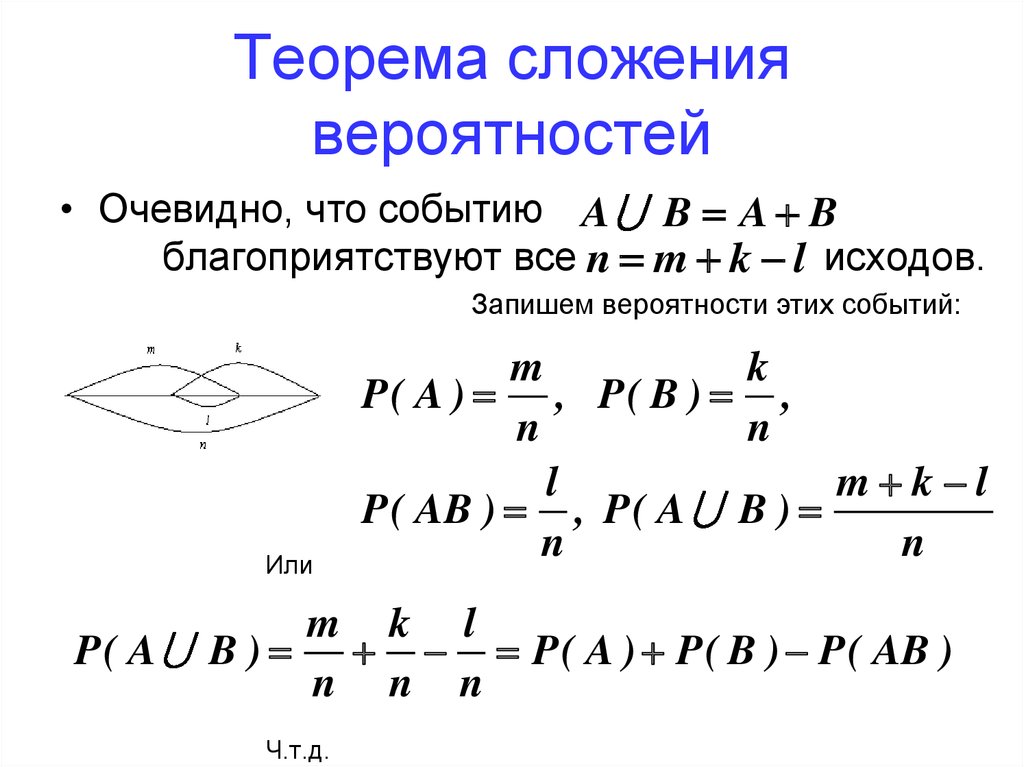
60.
Теорема сложениявероятностей
• Очевидно, что событию A B A B
благоприятствуют все n m k l исходов.
Запишем вероятности этих событий:
Или
P( A
m
k
P( A ) , P( B ) ,
n
n
l
m k l
P( AB ) , P( A B )
n
n
m k l
B ) P( A ) P( B ) P( AB )
n n n
Ч.т.д.
61. Теорема сложения вероятностей
• Для несовместных событий l = 0.• В этом случае
P( A B ) P( A ) P( B )
т.е. вероятность суммы несовместных событий равна
сумме вероятностей этих событий.
Следствие. Сумма вероятностей событий A1, A2,…,An ,
образующих полную группу, равна единице - как
вероятность достоверного события:
n
P( A
i 1
i
) P( U ) 1
62. Теорема сложения вероятностей
• Задача 1. В лотерее 1000 билетов. Наодин билет падает выигрыш в 500
рублей, на 10 по 100 рублей, на 50 – по
20 рублей и на 100 – по 5 рублей.
Какова вероятность выиграть на один
билет:
• а) не менее 20 рублей;
• б) любую сумму денег?
63. Теорема сложения вероятностей
• Решение: Обозначим события:A1 âû è ãðû ø 500 ð.í à î äè í áè ëåò ;
A1 âû è ãðû ø 100 ð.í à î äè í áè ëåò ;
A1 âû è ãðû ø 20 ð.í à î äè í áè ëåò ;
A1 âû è ãðû ø 5 ð.í à î äè í áè ëåò .
• Найдем вероятности этих простых
событий по формуле P M
:
N
64. Теорема сложения вероятностей
110
P( A1 )
0.001; P( A2 )
0.010;
1000
1000
50
100
P( A3 )
0.050; P( A4 )
0.100.
1000
1000
65. Теорема сложения вероятностей
• Введем обозначения для интересующихнас событий:
 âû è ãðû ø í å ì åí åå 20 ð. À1 À2 À3 À1 À2 À3
• - сумма 3-х несовместных событий;
Ñ âû è ãðû ø ëþ áî é ñóì ì û A1
A2
A3
A4
A1 A2 A3 A4 B A4
• - сумма 4-х несовместных событий.
66. Теорема сложения вероятностей
• Вычислим вероятности этих событий потереме сложения вероятностей
несовместных событий:
P( B ) P( A1 A2 A3 ) P( A1 ) P( A2 ) P( A3 )
0.001 0.010 0.050 0.061;
P( C ) P( A1 A2 A3 A4
P( B ) P( A4 ) 0.061 0.100 0.161.
67. Условие независимости событий
• Два события называютсянезависимыми, если вероятность
появления одного из них не зависит от
того, произошло или нет другое
событие.
68. Условие независимости событий
• Вероятность события, вычисленная впредположении, что одно или несколько
событий к этому моменту уже произошли,
называется условной вероятностью этого
события и обозначается:
• P( A B ) - условная вероятность события А
относительно события B;
• P( Â À ) - условная вероятность события В
относительно события A.
69. Условие независимости событий
• События А и В независимы, если ихусловные вероятности равны
“безусловным”,т.е. тот факт, что
событие В произошло к моменту
вычисления вероятности события А, не
изменил вероятности последнего
события.
70. Условие независимости событий
• Аналитическая запись условиянезависимости событий:
P( A B ) P( A )
или
P( B A ) P( B )
71. Условие независимости событий
• Условная вероятность события можетбыть получена по формуле
P( AB )
P( A / B )
P( B )
• Ясно, что если событие А не зависит от
события В, то и событие В не зависит
от А и наоборот.
72. Условие независимости событий
• Задача . Из колоды карт в 36 листовберут наугад одну карту. Рассмотреть
события:
À ï î ÿâëåí è å ò óçà
 ï î ÿâëåí è å êàðò û ÷åðí î é ì àñò è
Ñ ï î ÿâëåí è å ò óçà ï è ê
• Определить их парную независимость
(или зависимость).
73. Условие независимости событий
• Решение. Вычислим “безусловные”вероятности событий:
4
1
P( A )
;
36 9
18 1
1
P( B )
; P( C )
.
36 2
36
• Вычислим необходимые условные
вероятности:
2 1
P( A / B )
; P( A / C ) 1; P( B / C ) 1.
18 9
74. Условие независимости событий
• Выводы:• 1. P( A B ) P( A ) , следовательно,
события А и В независимы.
• 2. P( A Ñ ) P( A ) , следовательно,
события А и С зависимы.
• 3. P( Â Ñ ) P( Â ) , следовательно,
события В и С зависимы.
75. Условие независимости событий
..
Условие независимости
событий
• Задача . Зависимы или нет противоположные
события?
• Решение. Запишем условие независимости
для противоположных событий:
P( A À ) P( A ).
• А - случайное событие.
• Его вероятность P( A ) p 0.
• Но P( A À ) 0, т.к. A и A не совместны в
одном испытании.
• Вывод: события зависимы, т.к. P ( A А ) P ( A )
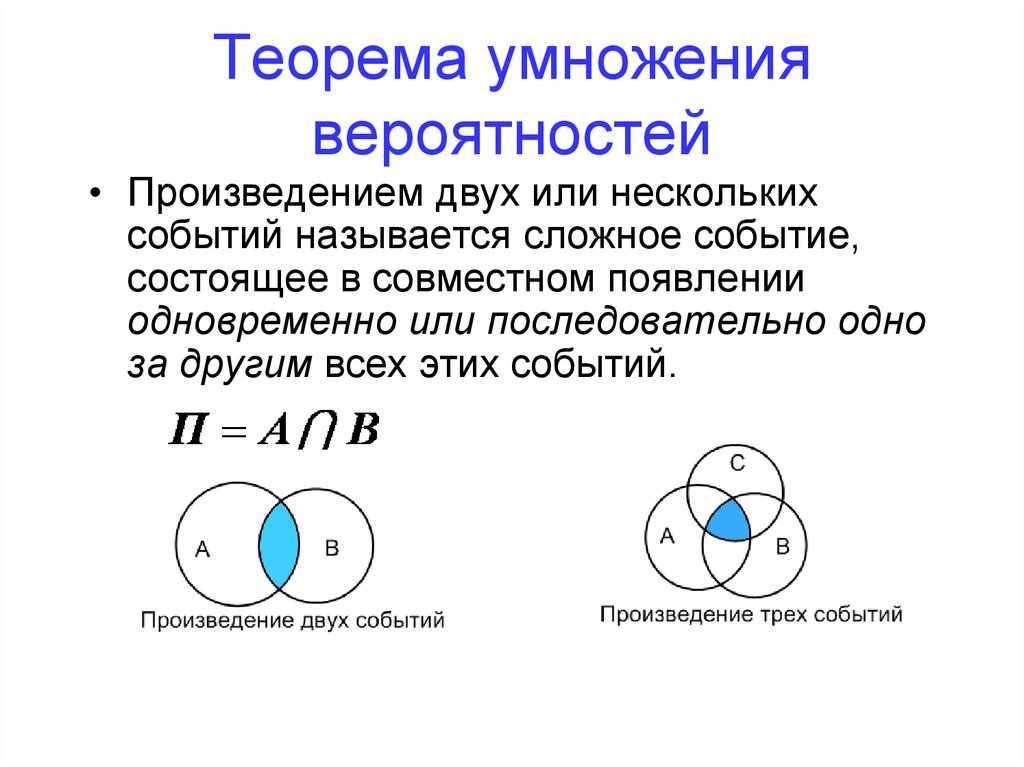
76. Теорема умножения вероятностей
• Произведением двух или несколькихсобытий называется сложное событие,
состоящее в совместном появлении
одновременно или последовательно одно
за другим всех этих событий.
77. Теорема умножения вероятностей
• Теорема. Вероятность произведениядвух зависимых событий равна
произведению безусловной
вероятности одного из них на условную
вероятность другого т.е.
P( A
B ) P( A )P( B / A ).
78. Теорема умножения вероятностей
• Доказательство:• n – общее число всех
возможных исходов опыта;
• m - благоприятствуют
наступлению события А;
• k –благоприятствуют
наступлению cобытия В;
• l исходов благоприятствуют
одновременно событиям А и В.
79. Теорема умножения вероятностей
• Запишем вероятности этих событий:m
k
l
P( A ) , P( B ) , P( AB ) .
n
n
n
• Условная вероятность события В:
l
P( B / A )
m
• Подставив все эти вероятности в доказываемую
формулу, получим тождество:
l m l
l l
;
,
n nm
n n
• что и подтверждает правильность доказываемой
формулы.
80. Теорема умножения вероятностей
• Аналогично для трех и более событий:• а) P( ABC ) P( A )P( B / A )P( C / AB )
• б) P( A1 A2 ...An ) P( A1 )P( A2 / A1 )P( A3 / A1 A2 )...
...P( An / A1 A2 A3 ...An 1 )
• Для независимых событий А и В: P( B / A ) P( B )
- по условию независимости событий.
• Поэтому для независимых событий
P( AB ) P( A )P( B ).
81. Теорема умножения вероятностей
• Задача. На карточках написаны буквыТ, Т, С и О. Карточки перемешаны и
перевернуты, а затем вскрываются по
одной.
• Определить вероятность того, что в
порядке появления букв получится
слово ТОСТ.
82. Теорема умножения вероятностей
• Решение.• Событие Â ÒÎ ÑÒ по определению
есть произведение событий.
• Вскрытые карточки обратно не
возвращаются, поэтому элементарные
события, образующие событие В
зависимы (изменяются условия опыта).
83. Теорема умножения вероятностей
• (Т, Т, С , О)• Поэтому для решения задачи применим
теорему умножения вероятностей
зависимых событий:
P(Â ) P ÒÎ ÑÒ P(T)P(O / T)P(C/TO)P(T/TOC)
• Тогда
2 1 1
1
P( B ) P( TOCT ) 1
0.083
4 3 2
12
84. Формула полной вероятности
• Является следствием обеихтеорем – сложения и умножения
вероятностей.
85. Формула полной вероятности
• Пусть требуется определитьвероятность события А, которое может
произойти вместе с одним из событий
• H1, H2,…, Hn,
• образующих полную группу и
называемых гипотезами.
86. Формула полной вероятности
• А – событие• H1, H2,…, Hn
• гипотезы
87. Формула полной вероятности
• Тогда вероятность события Авычисляется как
n
P( A ) P( H i )P( A / H i )
i 1
• т.е.как сумма произведений
вероятности каждой гипотезы на
вероятность события при этой гипотезе.
88. Формула полной вероятности
• Доказательство.• Так как гипотезы H i ( i 1,2,...,n )
образуют полную группу, то событие А
может появиться только в комбинации с
какой-либо из этих гипотез:
A H1
A
H2
A
H 1 A H 2 A ... H n A
...
Hn
A
89. Формула полной вероятности
• Так как гипотезы H i ( i 1,2,...,n )несовместны, то и комбинации
H 1 A, H 2 A, ..., H n A - тоже несовместны
• Тогда по теореме сложения
вероятностей:
P( A ) P( H 1 A ) P( H 2 A ) ... P( H n A )
n
P( H i A )
i 1
90. Формула полной вероятности
• Применяя к событиям H i A ( i 1,2,...,n )теорему умножения зависимых
событий, получим
n
P( A ) P( H i )P( A / H i )
i 1
,
• что и требовалось доказать.
91. Формула полной вероятности
• Задача. Имеются три одинаковые свиду урны. В первой - а белых и b
черных шаров, во второй – с белых и d
черных, а в третьей – только белые
шары.
• Некто подходит к одной из урн и
вынимает из нее один шар.
• Найти вероятность того, что этот шар
белый.
92. Формула полной вероятности
• Решение.A ï î ÿâëåí è å áåëî ãî ø àðà
• Событие
• Обозначим события-гипотезы:
• 1-я урна
• H1
2-я урна
3-я урна
H2
H3
• Т.к. выбор урны происходит случайно,
наугад, то вероятность каждой гипотезы
1
P( H 1 ) P( H 2 ) P( H 3 )
3
93. Формула полной вероятности
• Найдем вероятность вынуть белый шариз 1-й урны, т.е.
a
P( A / H 1 )
• затем – из 2-й:
• и, наконец, из 3-й:
a b
c
P( A / H 2 )
c d
P( A / H 3 ) 1
94. Формула полной вероятности
• По формуле полной вероятностинайдем
1 a
1 c
1
P( A )
1
3a b 3c d 3
1 a
c
(
1)
3 a b c d
95. Формула Байеса (теорема гипотез)
• Является следствием теоремыумножения вероятностей и
формулы полной вероятности.
96. Формула Байеса (теорема гипотез)
• Пусть имеется полная группанесовместных гипотез:
H1, H2,…, Hn
• Пусть вероятности этих гипотез до
опыта известны и равны
P( H 1 ), P( H 2 ), ...,P( H n )
• Пусть проведен опыт, в результате
которого наступило некоторое
событие А
97. Формула Байеса (теорема гипотез)
• Вопрос: как следует изменитьвероятности гипотез в связи с
наступлением этого события?
• По существу нужно найти «новую»
(условную) вероятность
P( H i / À )
• для каждой гипотезы.
98. Формула Байеса (теорема гипотез)
• По теореме умножения вероятностейимеем:
•P( A / H i ) P( A )P( H i / A ) P( H i )P( A / H i )
• или
P( A )P( H i / A ) P( H i )P( A / H i ) ,
• откуда
P( H i )P( A / H i ) ( i 1,2 ,...,n )
P( H i / A )
P( A )
99. Формула Байеса (теорема гипотез)
• Выражая P(A) с помощью формулыполной вероятности, имеем
P( H i / A )
P( H i )P( A / H i )
n
P( H
i 1
i
( i 1,2 ,...,n )
)P( A / H i )
• Формула Байеса дает возможность
«пересмотреть» вероятности гипотез
с учетом наблюдавшегося результата
опыта
100. Формула Байеса (теорема гипотез)
• Задача. Два стрелка стреляют в однумишень, делая каждый по одному выстрелу.
• Вероятность попадания в мишень для
первого стрелка равна 0.8, а для второго 0.4.
• После стрельбы в мишени обнаружена
пробоина.
• Найти вероятность того, что эта пробоина
принадлежит первому стрелку.
101. Формула Байеса (теорема гипотез)
• Решение. p1 = 0.8, p2 = 0.4• До опыта возможны следующие
гипотезы:
P( H 1 ) 0.2 0.6 0.12
H1 ( )
H2 ( )
H3 ( )
H4 ( )
. Их вер-ти:
P( H 2 ) 0.8 0.4 0.32
P( H 3 ) 0.8 0.6 0.48
P( H 4 ) 0.2 0.4 0.08
102. Формула Байеса (теорема гипотез)
• Условные вероятности наблюденногособытия
• А = {пробоина}
• при этих гипотезах равны:
P( A / H 1 ) 0 ; P( A / H 2 ) 0 ;
P( A / H 3 ) 1; P( A / H 1 ) 1
103. Формула Байеса (теорема гипотез)
• После опыта гипотезы H 1 и Н 2становятся невозможными.
• Вероятности гипотез H3 и Н4 будут
равны:
0.48 1
6
P( H 3 / A )
0.48 1 0.08 1 7
0.08 1
1
P( H 4 / A )
0.48 1 0.08 1 7
104. Формула Байеса (теорема гипотез)
• Следовательно, вероятность того, чтопробоина принадлежит первому
стрелку, равна
6
7
.
105. Испытания Бернулли. Формула Бернулли
• Испытания Бернулли – это повторныемногократные, независимые испытания
с двумя возможными исходами и с
вероятностью успеха, не меняющейся
от испытания к испытанию.
• Классический пример – многократное
бросание монеты.



































































































 Математика
Математика








