Готовимся к ОГЭ-2018. Задание 23. Графики функций

1. Готовимся к ОГЭ – 2018 Задание 23 Графики функций

ГОТОВИМСЯ К ОГЭ – 2018
ЗАДАНИЕ 23
ГРАФИКИ ФУНКЦИЙ
Смирнова Марина Александровна,
учитель математики
МОУ Оковецкая СОШ,
д. Оковцы, Тверская обл.

2.

Цель урока:
подготовка к ОГЭ;
отработка умений решать задачи,
связанные с построением графиков
различных функций

3.

Постройте график функции y 2 x2 1
2x x
и определите, при каких
значениях k прямая y=kx
имеет с графиком ровно одну
общую точку
1) Найдем область определения
функции: х 0, х 0,5
1
у
1
0,5
2
2x 1
2х 1
1
y 2
2 x x х(2 х 1) х
х 0, х 0,5
y kx, ( 0,5; 2)
k 4
1
0
2) Упростим правую часть
формулы:
k ( 0,5) 2
y kх
Ответ: k=4
х

4.

x 2
Постройте график функции y 3 2
x 2x
и определите, при каких
значениях m прямая y=m
не имеет с графиком
общих точек
1) Найдем область определения
функции: х 0, х 2
2) Упростим правую часть
формулы:
x 2
х 2
1
y 3 2
3
3
x 2x
х ( х 2)
х
х 0, х 2
Ответ: m=3, m=3,5
2
у
3,5
у 3,5
у 3
1
1
2
0
х

5.

х 2 , х 1,
Постройте график функции
y 1
и определите, при каких
, х 1
х
значениях параметра с прямая
y=с имеет с графиком ровно одну
общую точку
3
у
Область определения
функции: х ( ; )
1
1
1
0
Ответ: при -1< c ≤ 0
1
х

6.

( х 2 5 х 6 )2
Постройте график функции y
x 3
и определите, при каких
значениях а прямая y=а не имеет
с графиком данной функции
общих точек
1) Найдем область определения
функции: х 2 5 х 6 0,
х 3 0
х ;2 3;
4
у
1
1
0
2
2
2) Упростим правую часть
формулы :
( х 2 5 х 6 )2 х 2 5 х 6
y
x 3
х 3
( х 2)( х 3)
х 2
х 3
Ответ: а 0;1
3
х

7.

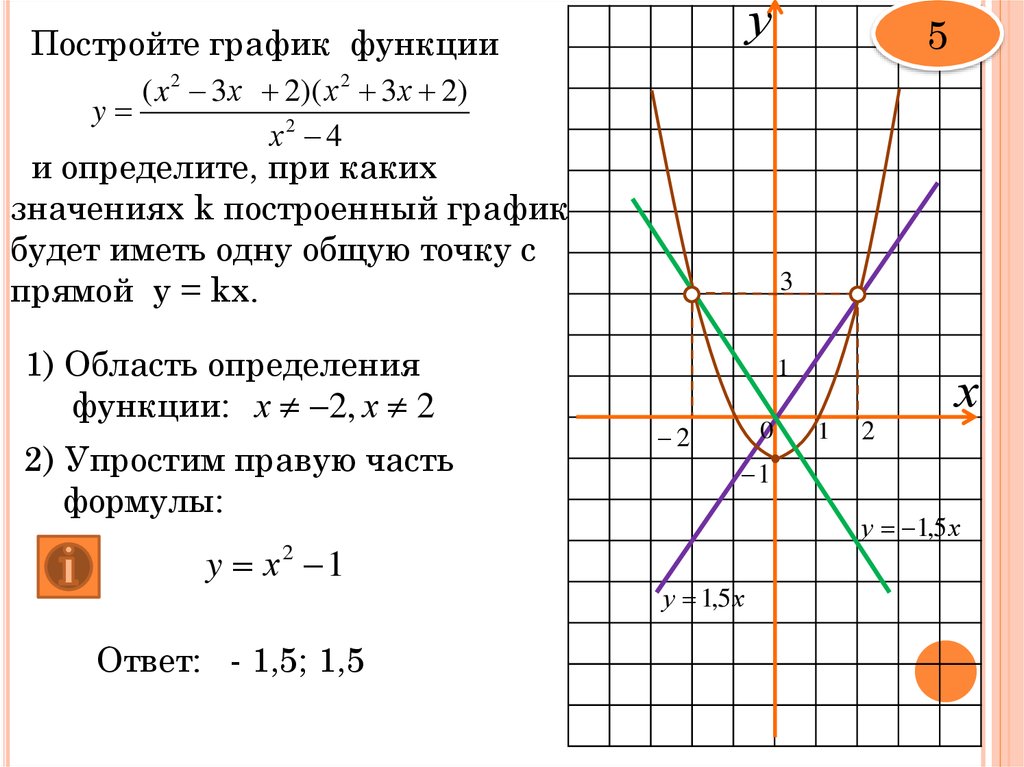
у
Постройте график функции
5
( x 2 3 х 2)( х 2 3 х 2)
y
х2 4
и определите, при каких
значениях k построенный график
будет иметь одну общую точку с
прямой у = kx.
1) Область определения
функции: х 2, х 2
2) Упростим правую часть
формулы:
y х2 1
Ответ: - 1,5; 1,5
3
1
2
0
х
1
2
1
у 1,5 х
у 1,5 х

8.

у
Постройте график функции
6
x 4 13 х 2 36
y
( х 3)( х 2)
и определите, при каких
значениях параметра с
прямая y=с имеет с графиком
ровно одну общую точку
1) Область определения
функции: х 3, х 2
2) Упростим правую часть
формулы:
1
2
0
y х2 х 6
Ответ: с = -6,25
х
0,5
6,25
1
3

9.

1
х
3,5
х
3,5
)
Постройте график функции y (
2 3,5 х 3,5 х
и определите, при каких
значениях m прямая y=m имеет
у
с графиком ровно одну общую
точку
1) Область определения
1
функции: х 0
3,5
1
2) Упростим правую часть
формулы:
х
, х 3,5;0 3,5;
3,5
y
3,5 , х ;3,5 0;3,5
х
Ответ: m=1, m=-1
0 1
2
7
3,5
х

10.

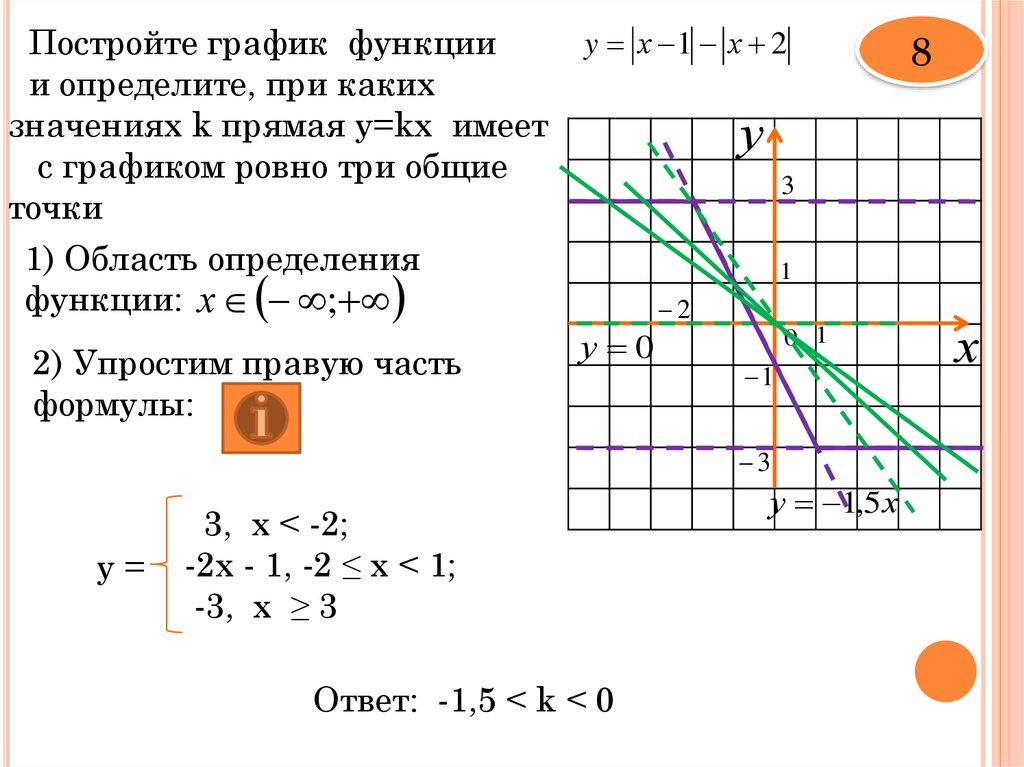
Постройте график функции
и определите, при каких
значениях k прямая y=kx имеет
с графиком ровно три общие
точки
1) Область определения
функции: х ;
2) Упростим правую часть
формулы:
y х 1 х 2
у
3
1
2
у 0
0 1
1
3
у=
8
3, х < -2;
-2х - 1, -2 ≤ х < 1;
-3, х ≥ 3
Ответ: -1,5 < k < 0
у 1,5 х
х

11.

у
Постройте график функции
у = │х – 2│ + │х² - 9│
и определите, при каких
значениях а прямая y = а
имеет с графиком
три общие точки
1) Найдем область определения
функции: х ;
2) Преобразуем правую часть
формулы:
х² - х - 7, х < -3;
-х² - х + 11, -3 ≤ х < 2;
у = -х² + х + 7, 2 < х ≤ 3;
х² + х - 11, х > 3
Ответ: а = 5, а = 11,25
у 11
9
1
4
5
1
3
1
0
2
3
х

12. Памятка:

ПАМЯТКА:
1)
2)
3)
4)
Найдем область определения функции
Упростим или преобразуем правую часть
формулы, если это возможно
Построим график функции
Ответим на вопрос задачи, используя
построенный график

13.

( x 2 3 х 2)( х 2 3 х 2)
у
2
х 4
( х 1)( х 2)( х 1)( х 2)
( х 2)( х 2)
х 2 1, х 2, х 2
ах вх с а( х х1 )( х х2 )
2

14.

x 4 13 х 2 36 ( х 2 4)( х 2 9)
у
( х 3)( х 2)
( х 3)( х 2)
( х 2)( х 2)( х 3)( х 3)
( х 3)( х 2)
( х 2)( х 3) х х 6,
2
х 3, х 2

15.

1 х 3,5
х 3,5
y (
)
2 3,5 х 3,5 х
1 х 2 3,52 х 2 3,52
(
)
2
3,5 х
3,5 х
y
х 2 3,52
( х 3,5)( х 3,5)
3,5 х
3,5 х
+
-3,5
0
-
+
3,5
1
х
3,5
х
3,5
(
)
2 3,5
х
3,5
х
1 х 2 3,52
х 2 3,52
(
)
2
3,5 х
3,5 х
1 2х2
х
2 3,5 х 3,5 , х 3,5;0 3,5;
2
1
2
3
,
5
3,5
, х ;3,5 0;3,5
3,5 х
х
2

16.

у =│х – 1│ - │х + 2│
-
-
-
+
+
1
+
-2
х
х
Если х < -2, то у = 1 - х - (- х - 2 ) = 3
Если -2 ≤ х < 1, то у = 1 - х - (х + 2) = -2х - 1
Если х ≥ 1, то у = х - 1 - (х + 2) = -3
у=
3, х < -2;
-2х - 1, -2 ≤ х < 1;
-3, х ≥ 3

17.

у =│х – 2│ + │х² - 9│
-
-
+
-3
+
2
+
-
+
3
х
х
Если х < -3, то у = 2 - х + х² - 9 = х² - х - 7
Если -3 ≤ х < 2, то у = 2 - х - х² + 9 = -х² - х + 11
Если 2 < х ≤ 3, то у = х - 2 - х² + 9 = -х² + х + 7
Если х > 3, то у = х – 2 + х² - 9 = х² + х - 11
у=
х² - х - 7, х < -3;
-х² - х + 11, -3 ≤ х < 2;
-х² + х + 7, 2 < х ≤ 3;
х² + х - 11, х > 3

18. источники

ИСТОЧНИКИ
Задание 1
№ 153
https://oge.sdamgia.ru/test?theme=87
Задание 2
№357531
https://oge.sdamgia.ru/test?pid=357531
Задание 3
№ 75 https://oge.sdamgia.ru/test?theme=88
Задание 4
№ 311565
https://oge.sdamgia.ru/test?theme=88
Задание 5
№ 23 Тренировочный вариант №136
ОГЭ-9 http://alexlarin.net/gia/trvar136_oge.html
Задание 6
№ 49 https://oge.sdamgia.ru/test?theme=23
Задание 7
№ 338314
https://oge.sdamgia.ru/test?theme=88
Задание 8
№ 23 Тренировочный вариант №133
ОГЭ-9 http://alexlarin.net/gia/trvar133_oge.html
Задание 9
№ 23 Тренировочный вариант №113
ОГЭ-9 http://alexlarin.net/gia/trvar113_oge.html