Разбор заданий ОГЭ №22

1.

Разбор заданий ОГЭ
№22

2.

Задание 22
Функции и их свойства.
Графики функций.
• Кусочно-непрерывные
функции
• Параболы
• Гиперболы
• Разные задачи

3.

Алгоритм решения задач №22.
1. Преобразовать выражение, которым
задается функция.
2. Рассмотреть ОДЗ.
3. Построить график, с учётом
ОДЗ.(учитывая точки разрыва
функции)
4. Провести прямые у=m или у= kx,
согласно условию задачи
5. Записать ответ.

4.

Критерии оценивания:

5.

1)Построим график функции у=х-3
х
0
3
у
-3
0
при х<3
2017-18год.
2) Построим график функции у=-1,5х+4,5 при 3≤ х≤4
Х
3
4
у
0
-1,5
3) Построим график функции у= 1,5х-7,5 при х˃4
Х
4
6
у
-1,5
1,5

6.

у
0
У=0
У=-1,5
1,5
01
-1,5
-3
х
3 4

7.

• Прямая у=m имеет с графиком функции
ровно две общие точки при m= -1.5 и m=0
• Ответ: m= -1.5 и m=0

8.

9.

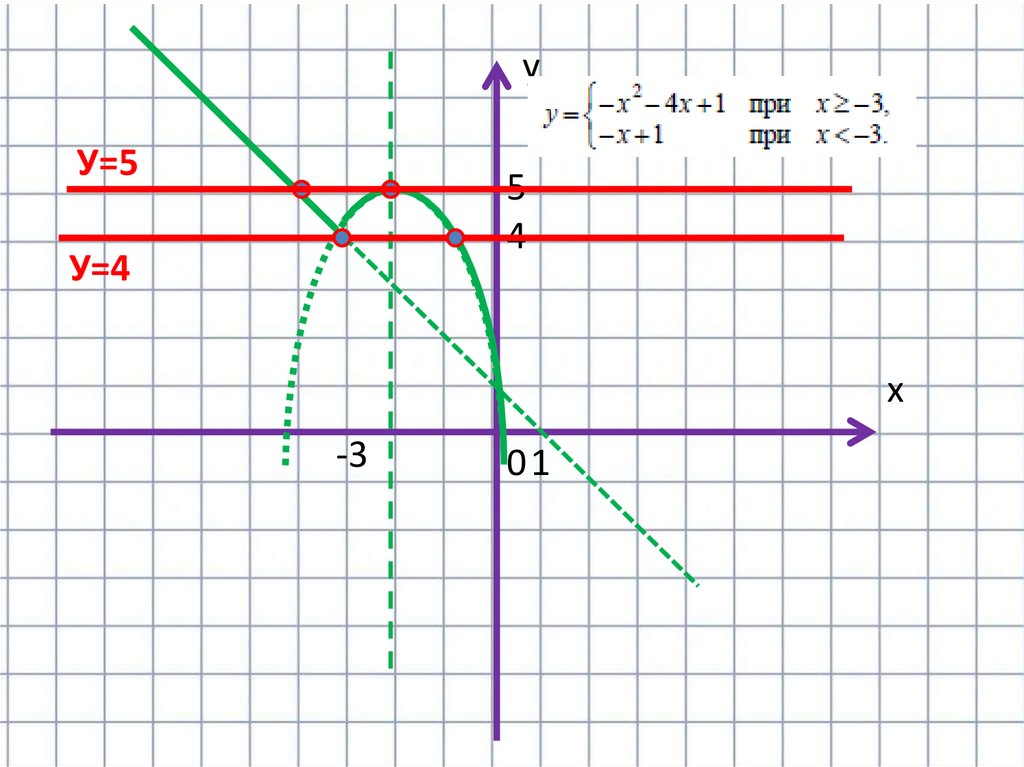
1) Построим график функции у= -х²-4х+1 при х≥-3
а)Находим координаты вершины параболы
Х=-b/2a х= 3
-(-4)/-2*1=-2
У=-(-2)²-4(-2)+1=5
б) Ось симметрии х=-2
-3
-2
-1
0
1
в)Дополнительные точки: Х
У
4
5
4
2) Построим график функции у=-х+1 при х<-3
х
-3
0
у
4
1
1
-4

10.

у
У=5
5
4
У=4
х
-3
01

11.

Прямая у=m имеет с графиком ровно две
общие точки, если она проходит через
вершину параболы или через точку
(-2;3).
Получаем, что m=4 или m= 3.
Ответ : 3;4

12.

13.

14.

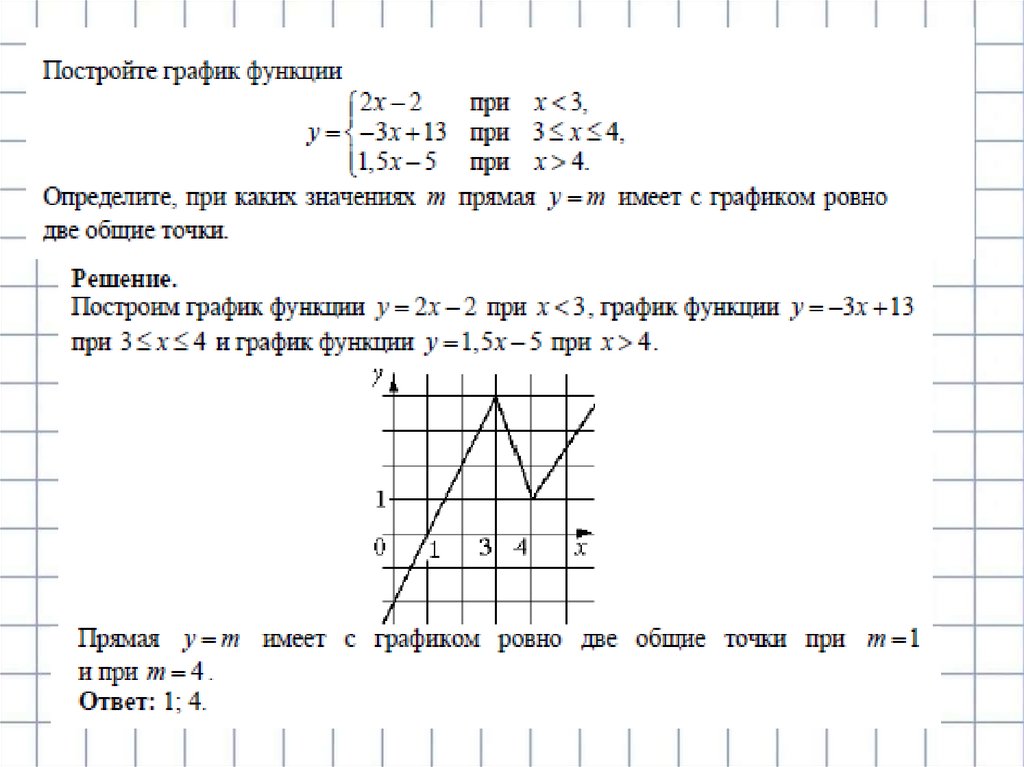
Постройте график функции
и определите,
при каких значениях m прямая y = m имеет с графиком ровно две общие точки.
Решение:
Построим график функции y = 2,5x при x < 2 и
график функции y = x2 − 6x + 13 при x ≥ 2.
Прямая y = m имеет с графиком ровно
две общие точки при m = 4 и при m = 5 .
Ответ: 4; 5.

15.

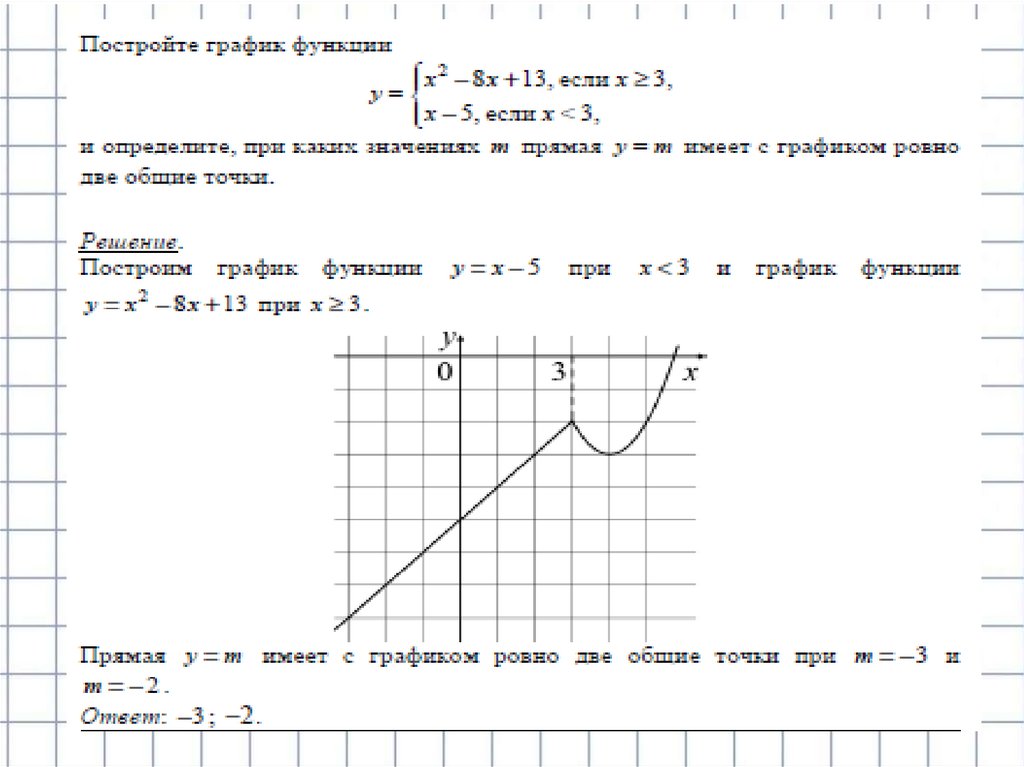
Постройте график функции
и определите,
при каких значениях m прямая y = m имеет с графиком ровно две общие точки.
Решение:
Построим
график функции
y = 2,5x при x < 2 и
Построим график функции
у=-х²-4
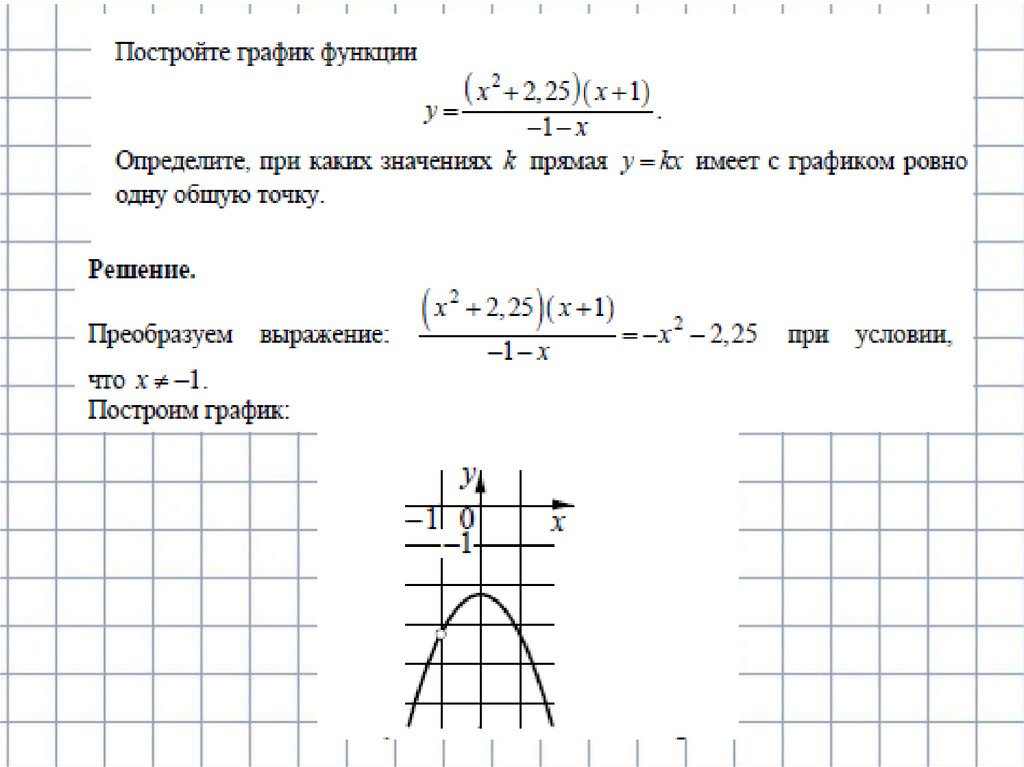
при х≠1
функции y = x − 6x + 13 при x ≥ 2.
а) Координаты вершиныграфик
параболы
(0;-4)
Прямая y = m имеет с графиком ровно
б)Ось симметрии х=0 две общие точки при m = 4 и при m = 5 .
в) Дополнительные точки:
2
Х
-2
-1
0
1
2
У
-8
-5
-4
-5
-8

16.

У=-5х
у
х
-2 -1 0 1 2
-4
-5
У=-4х
У=4х

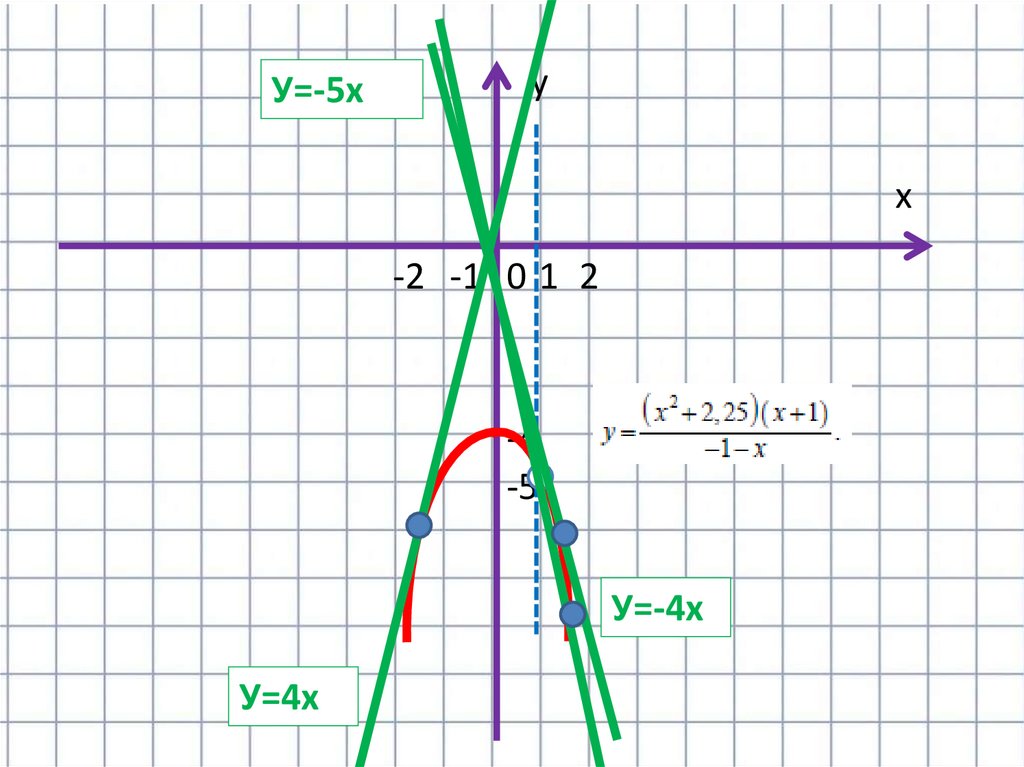
17.

Прямая у=кх имеет с графиком ровно одну
общую точку, если она проходит через точку
(1;-5) или если уравнение –х²-4=кх имеет один
корень.
Дискриминант уравнения х²+кх+4=0 равен к²16. и он должен быть равен 0.Получаем , что к=
-5, к=-4, к=4.
Ответ: -5;-4;4

18.

19.

20.

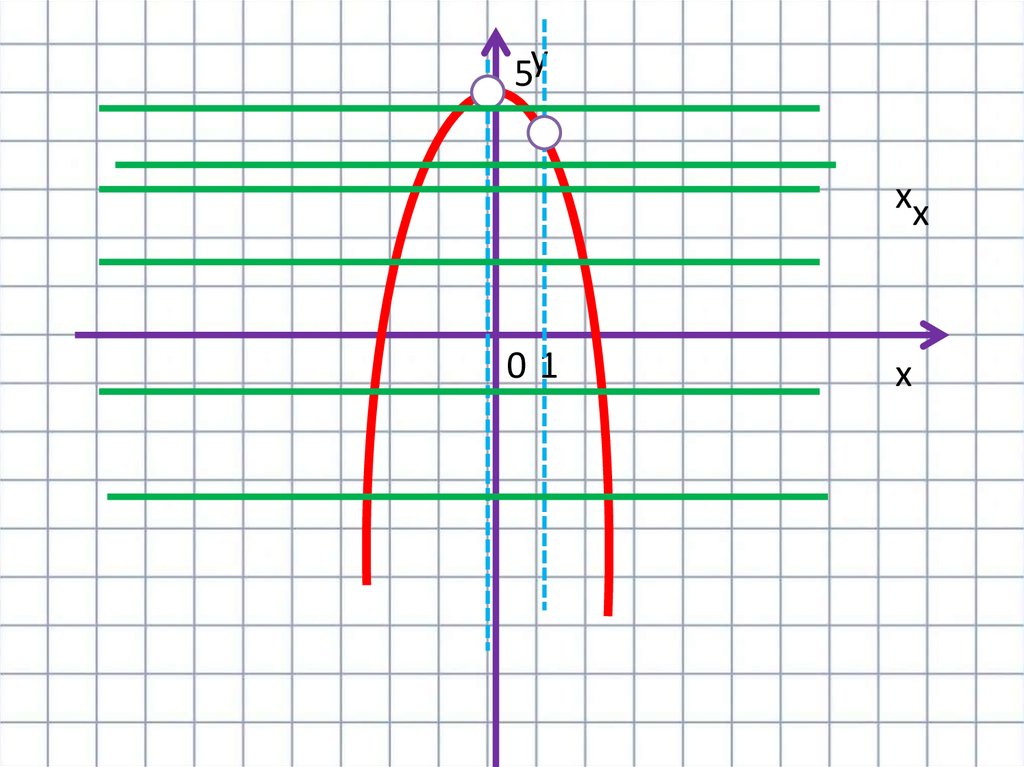
Построим график функции у=5-х²
а)Координаты вершины параболы: (0;5)
б) Ось симметрии : х=0
в)Дополнительные точки:
Х
-3
-2
-1
0
1
2
3
У
-4
1
4
5
4
1
-4

21.

5у
хх
01
х

22.

• Прямая у=m имеет с графиком ровно две
общие точки при m<4 и при 4< m<5
• Ответ при mє(-∞;4),(4;5)

23.

24.

25.

26.

27.

28.

29.

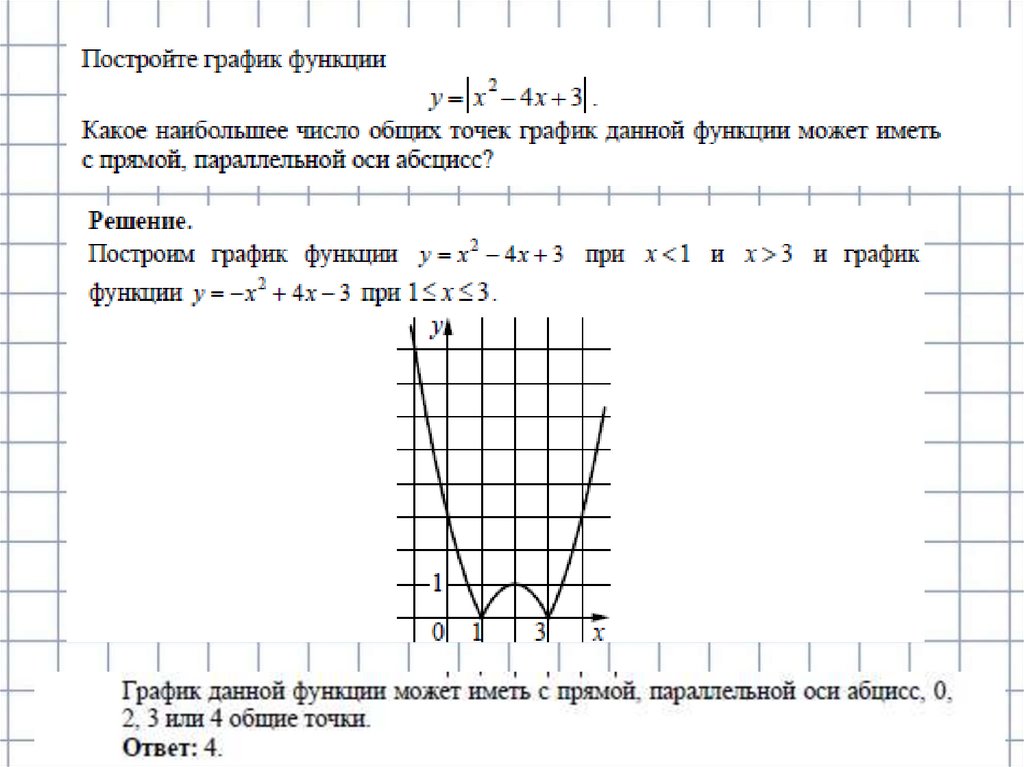
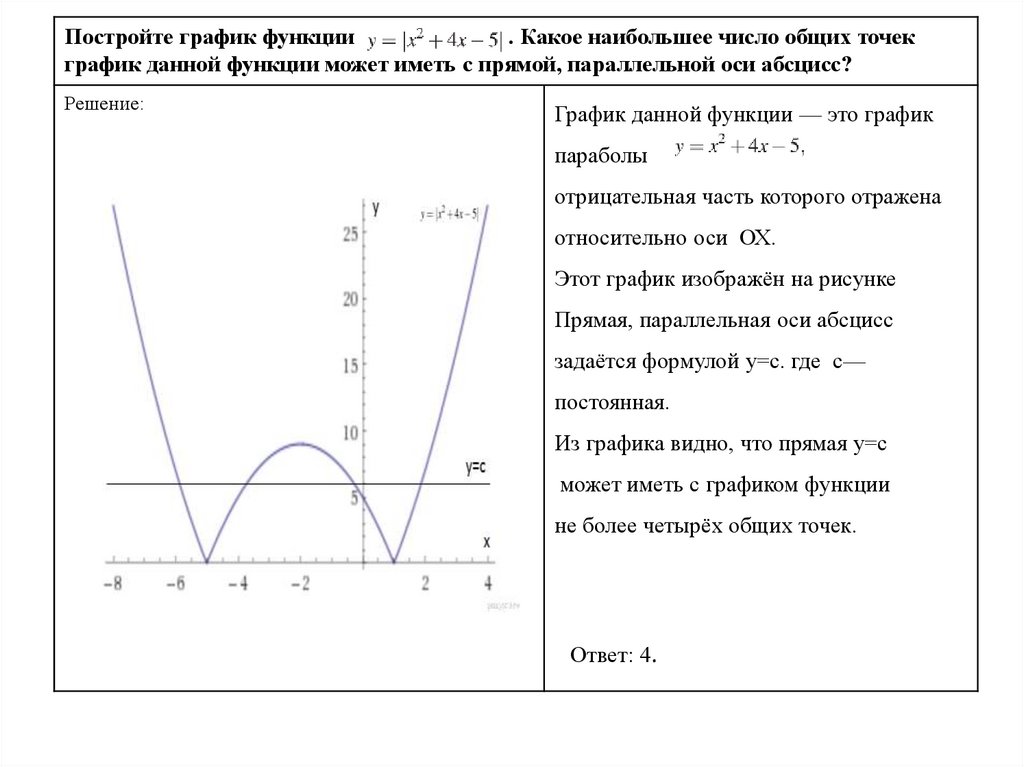
Постройте график функции
. Какое наибольшее число общих точек
график данной функции может иметь с прямой, параллельной оси абсцисс?
Решение:
График данной функции — это график
параболы
отрицательная часть которого отражена
относительно оси ОХ.
Этот график изображён на рисунке
Прямая, параллельная оси абсцисс
задаётся формулой у=с. где с—
постоянная.
Из графика видно, что прямая у=с
может иметь с графиком функции
не более четырёх общих точек.
Ответ: 4.

30.

31.

32.

33.

34.

35.

1. Данный материал взят из экзаменационных
работ прошлых лет.
2. РЕШУ ОГЭ. Образовательный портал для
подготовки к экзаменам . Математика
3. ФИПИ-открытый банк заданий ОГЭ.
4. http://mathematichka.ru/oge9/Graph23/problems23
_Graf_OGE.html
5. https://www.time4math.ru/oge
6. https://yourtutor.info/решение-задания-23-из-огэпо-математике
7. https://www.youtube.com/watch?v=ZAE-CkppQP4
Спасибо за внимание.