Вычислительная механика. Основные понятия МКЭ

1. Лекция Вычислительная механика Основные понятия МКЭ

К.т.н., доцент каф. ВМиМ
Каменских Анна Александровна
239-15-64

2.

Основные понятия МКЭ, обозначения и соотношения
Q
Qy
Qx
l
(e)
V
Px
g
i
j
k
P
Py
Первый этап: построение сетки – аппроксимация исходной области набором простых по форме
подобластей (конечных элементов (КЭ)). Замена не точна. КЭ связаны друг с другом в некоторых точках,
расположенных на их границах – узлах КЭ. Основными неизвестными считаются перемещения этих точек
(узлов).
Второй этап: Выбирается система функций, однозначно определяющих неизвестные (перемещения)
внутри КЭ, через неизвестные в узлах КЭ – функции формы. Поля неизвестных внутри элемента
аппроксимируются через неизвестные в узлах КЭ.
Третий этап: С использованием соотношений ТУ через введённые аппроксимации полей
перемещений определяются деформации, а затем и напряжения в любой точке КЭ. В результате
деформации и напряжения внутри КЭ оказываются выражены через перемещения узлов КЭ.
Четвёртый этап: Записываются условия равновесия системы КЭ, отражающие тот факт, что система
внутренних сил упругости, приведённых к узлам КЭ, должна уравновешивать систему внешних сил,
приведённую к узлам сетки. Условия равновесия записываются в жёсткостной форме и представляют
собой СЛАУ относительно перемещений в узлах сетки. Проще говоря, учитывается физическая сторона
решаемой задачи будь-то ТУ или другой.

3.

ij , j x gi x 0
(e)
vi
i ui
vj
j
ij x
vk
uj
k
uk
1
ui , j x u j ,i x
2
ij x x ij 2 ij x
ui x Ui
ij x n j Pi
x y

4.

Построение КЭ соотношений из принципа возможных перемещений
Принцип возможных перемещений состоит в том, что для
тела находящегося в состоянии равновесия и получившего в
(e)
P
этом состоянии бесконечно малое возможное смещение точек,
g
работа внутренних сил на возможное перемещение точек
равна работе внешних сил на эти возможные перемещения.
j
k
i
Rj
Работа внешних сил
AFe Rx j u j Ry j j ... Qxi ui Qyi i ... g x u g y ... dV e px u p y ... d e
e
Ve
R Q f
AF
e
T
e
e
f N e e
R Q
e
T
e
e
AFe
AFe
T
e
Ve
f N e e
AFe
T
T
e
e
T
Ve
T
R Q
e
T
e
e
g dV e f T p d e
e
f e
T
N e
T
g dV
e
T
N e
T
e
T
e
N e
T
p d e
T
T
e
e
e
e
e
e
R Q N g dV N p d
Ve
e
e
Fge
Fpe
Fge
Ve
N e
T
g dV e Fpe
e
N e
T
p d e

5.

Работа внутренних сил
A e
V
T
e
V
dV e
Ve
T
e
e
T
Be
T
V
e
T
B e e
D B dV
e
e
e
0
e
e
e
0
K e
T
dV e
T
D B dV
F e0
Ve
e T e e
e
B
e e
D
B
dV
e
V
A e
Ve
Be e
Ve
e
x x y y xy xy dV e
De 0 0
A e
A e
ij ij dV e
T
e
Ve
T
e
0
e T e
e
B
e
D
dV
0
e
V
T
T
e
B 0 dV
e
V
K e e F e F e
0
0
T
B e De Be dV e
B e De 0 dV e
F e0
0
T
e
B
dV
0
Ve
e

6.

A e AFe
K F F R Q F F 0
e
T
e
K e e F e F e
0
0
T
e
e
e
T
e
0
0
e
0
(2)
i
(3)
(5)
Qx(5)
i
(5)
j
R e Q e Fge Fpe
e
e
p
F F F F F R
e
e
g
Qxe
i
(4)
e
g
Выражение в скобках равно нулю!
i
(e)
T
e
k
(1)
e
Q y(5)
e
0
e
p
e
0
Qye
0
i
e
0
e
Qe 0
e
e
i
K e e F e Q e 0
e e
e
K
F
e
e
K e e F e Q e
Q K F
e
e
K F
e
e

7.

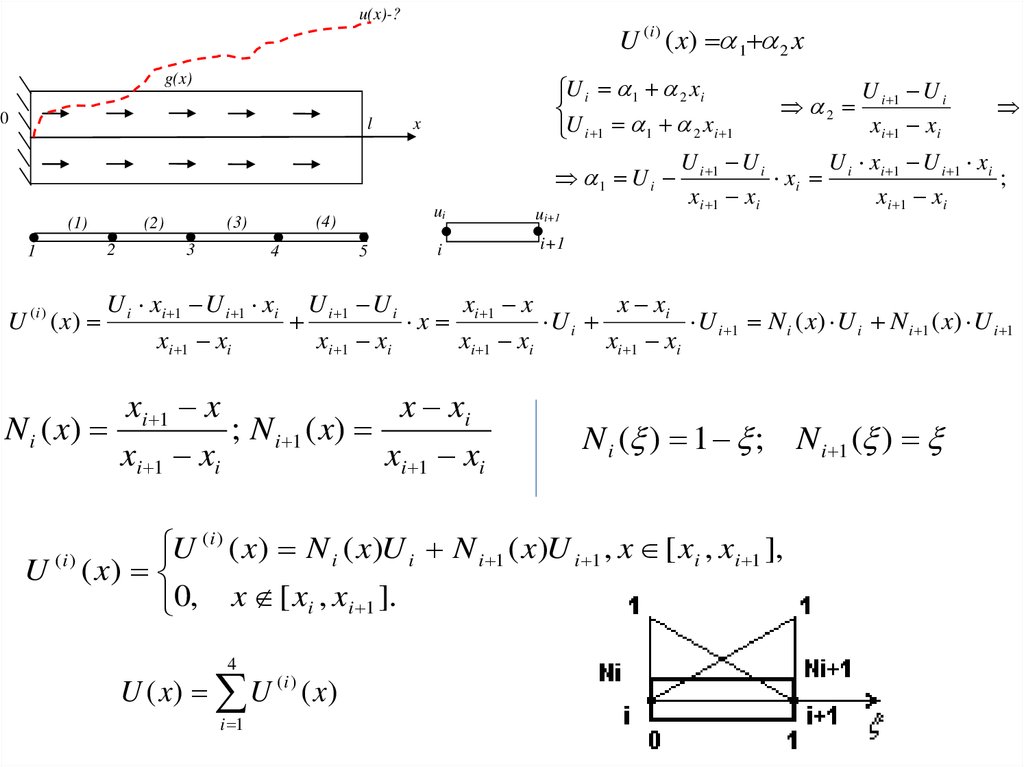
u(x)-?
U (i ) ( x) 1 2 x
U i 1 2 xi
U i 1 1 2 xi 1
g(x)
0
l
x
1 U i
(1)
1
U ( i ) ( x)
2
(4)
(3)
(2)
3
4
5
ui
ui+1
i
i+1
2
U i 1 U i
xi 1 xi
U i 1 U i
U x U i 1 xi
xi i i 1
;
xi 1 xi
xi 1 xi
U i xi 1 U i 1 xi U i 1 U i
x x
x xi
x i 1
U i
U i 1 N i ( x) U i N i 1 ( x) U i 1
xi 1 xi
xi 1 xi
xi 1 xi
xi 1 xi
xi 1 x
x xi
N i ( x)
; N i 1 ( x)
xi 1 xi
xi 1 xi
N i ( ) 1 ; N i 1 ( )
(i )
U
( x) N i ( x)U i N i 1 ( x)U i 1 , x [ xi , xi 1 ],
U (i ) ( x)
0, x [ xi , xi 1 ].
4
U ( x) U (i ) ( x)
i 1

8.

4
П П П F П АF П i AFi
i 1
1
П F
2
i
xi 1
xi
1
x x dx EF
2
xi 1
A F g ( x)U ( x)dx
xi
EF
П
2
i
xi
xi
U 1 0,
i
F
xi 1
xi 1
N i 1
EF
N i
Ui
U i 1 dx
x
2
x
xi 1
xi
Ui
U i 1
xi 1 xi xi 1 xi
U
x
П
0, i 2,5
U i
2
EF
dx
2( xi 1 xi ) 2
EF
U i 1 U i 2 1
2
xi 1 xi
xi 1
A F g ( x) N iU i N i 1U i 1 dx
i
F
xi
2
xi 1
2
U
U
dx
i
1
i
xi

9.

3
2
П П 1 П 2
EF
EF
U 3 U 2 F g ( x) N 2 ( x)dx
U 2 F g ( x) N 2 ( x)dx
U 2 U 2 U 2 ( x2 x1 )
( x3 x 2 )
x1
x2
x
x
K 22(1) K 22( 2)U 2 K 23( 2)U 3 F2(1) F2( 2) 0
3
4
П П 2 П 3
EF
EF
U 3 U 2 F g ( x) N 3 ( x)dx
U 4 U 3 F g ( x) N 3 ( x)dx
U 3 U 3 U 3 ( x3 x 2 )
( x 4 x3 )
x2
x3
x
x
K 33( 2)U 3 K 32( 2)U 2 K 33(3)U 3 K 34(3)U 4 F3( 2) F3(3) 0
П
( 3)
( 3)
( 4)
( 4)
K 44
U 4 K 43
U 3 K 45
U 5 K 44
U 4 F4(3) F4( 4) 0
U 4
П
( 4)
( 4)
K 54
U 4 K 55
U 5 F5( 4 ) 0
U 5
K
( 2)
23
EF
EF
( 2)
( 2)
( 2)
, K 32
, K 23
K 32
x3 x 2
x3 x 2

10.

(1)
(2)
(2)
(1)
(2)
K 22
K 22
U
K
U
F
F
2
23
3
2
2
(2)
K 32 U 2 K 33(2) K 33(3) U 3 K 34(3)U 4 F3(2) F3(3)
(3)
(3)
(4)
(4)
(3)
(4)
K
U
K
K
U
K
U
F
F
44
4
45
5
4
4
43 3 44
K 54(4)U 4 K 55(4)U 5 F5(4)
K U F
K
(1)
22
K
( 2)
22
K
( 2)
23
0
( 2)
K 32
( 2)
( 3)
K 33
K 33
( 3)
K 34
0
( 3)
K 43
( 3)
( 4)
K 44
K 44
0
0
( 4)
K 54
(1)
( 2)
F
F
U
0
2
2
2
U F ( 2 ) F ( 3)
0 3 3
3
( 3)
( 4)
( 4)
U
K 45 4 F4 F4
( 4)
K 55
U 5 F5( 4 )