Вычислительная механика. Конечные элементы с нелинейной аппроксимацией

1. Лекция Вычислительная механика Конечные элементы с нелинейной аппроксимацией

К.т.н., доцент каф. ВМиМ
Каменских Анна Александровна
239-15-64

2.

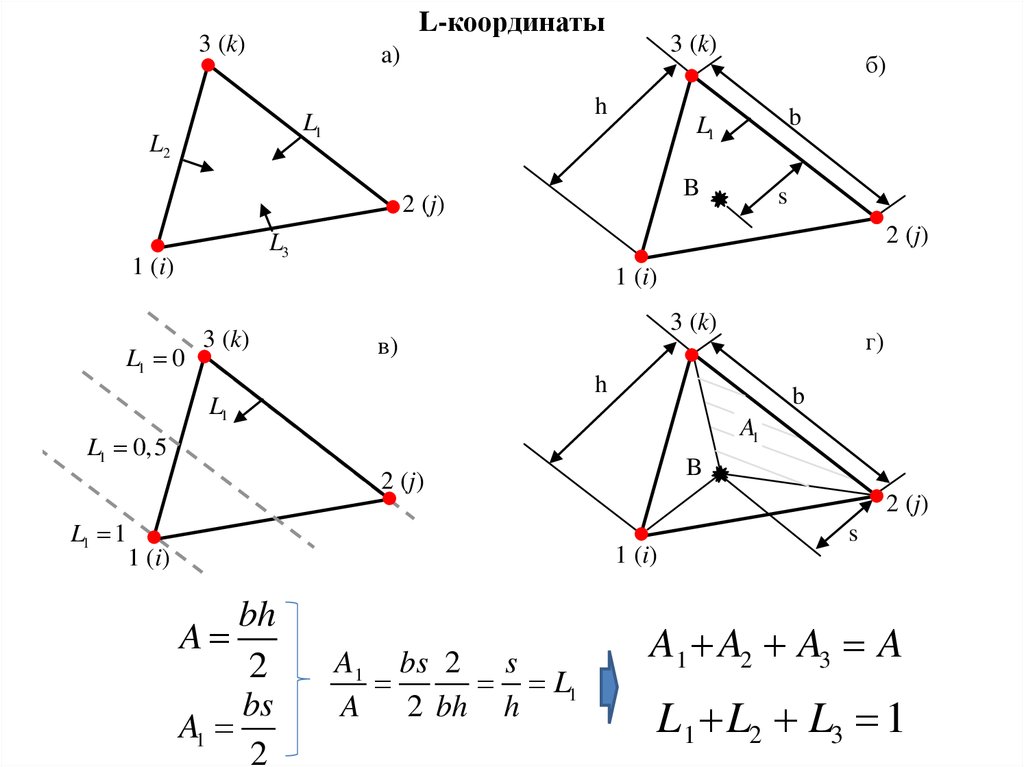
L-координаты
3 (k)
3 (k)
a)
h
L1
L2
b
L1
B
2 (j)
s
2 (j)
L3
1 (i)
1 (i)
L1 0
3 (k)
3 (k)
в)
г)
h
L1
b
A1
L1 0,5
B
2 (j)
L1 1
б)
2 (j)
1 (i)
1 (i)
bh
A
2
bs
A1
2
A1 bs 2 s
L1
A 2 bh h
s
A1 A2 A3 A
L 1 L2 L3 1

3.

При деформации элемента L-координаты не изменяются! По сути Lкоординаты удовлетворяют всем требованиям, предъявляемым к функциям
формы, то есть их можно использовать в качестве функций формы элемента.
Ni L1 , N j L2 , N k L3
1, в узле с номером i
L1
0 , в других узлах
СЛАУ
x L1 xi L2 x j L3 xk
y L1 yi L2 y j L3 yk
1 L1 L2 L3
1
L1
a bi x ci y
e i
2A
a !b !c !
a b c
e
e
L
L
L
dA
2
A
1
2
3
e
a b c 2 !
A
*
ai x j ym xm y j ,
bi y j ym ,
ci xm x j ,
a !b !
a b
e
e
L
L
d
e 1 2
(a b 1)!
t N
Fge
Ae
e T
i, j,m.
g dAe
N i dAe L1dAe
1! 0! 0!
2
1
2 Ae Ae Ae
6
3
1 0 0 2 !
Ae
Ae
L11L02 L03dAe
Ae
* Martin A. Eisenberg, Lawrence E. Malvern On finite element integration in natural co-ordinate // International Journal for
Numerical Methods in Engineering Volume 7, Issue 4, 1973.

4.

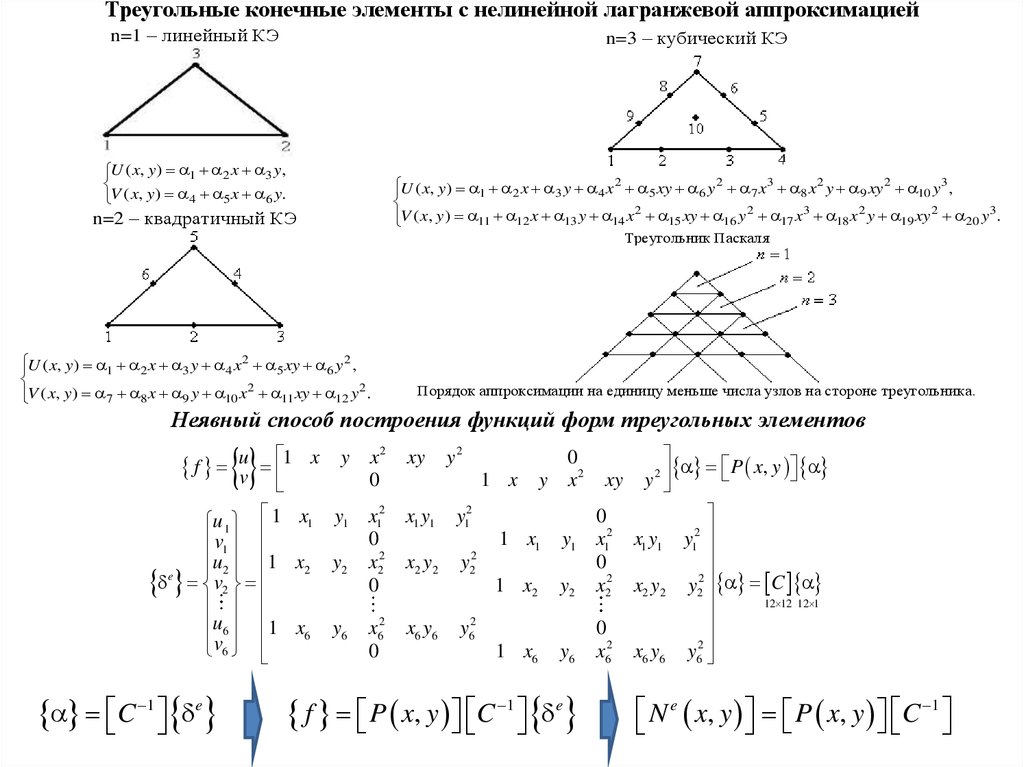
Треугольные конечные элементы с нелинейной лагранжевой аппроксимацией
n=1 – линейный КЭ
n=3 – кубический КЭ
U ( x, y ) 1 2 x 3 y,
V ( x, y ) 4 5 x 6 y.
2
2
3
2
2
3
U ( x, y ) 1 2 x 3 y 4 x 5 xy 6 y 7 x 8 x y 9 xy 10 y ,
2
2
3
2
2
3
V ( x, y ) 11 12 x 13 y 14 x 15 xy 16 y 17 x 18 x y 19 xy 20 y .
n=2 – квадратичный КЭ
Треугольник Паскаля
2
2
U ( x, y ) 1 2 x 3 y 4 x 5 xy 6 y ,
2
2
V ( x, y ) 7 8 x 9 y 10 x 11xy 12 y .
Порядок аппроксимации на единицу меньше числа узлов на стороне треугольника.
Неявный способ построения функций форм треугольных элементов
f uv 1 x
y
u 1 1 x1 y1
v1
u2 1 x2 y2
e
v2
u6 1 x6 y6
v6
C 1 e
x2
0
xy
x12
0
x22
0
x1 y1
x62
0
y2
1 x
x2 y2
x6 y6
0
y x2
y12
y
2
2
xy
1 x1
y1
1 x2
y2
0
x12
0
x22
y6
0
x62
y62
1 x6
f P x, y C 1 e
P x, y
y
2
x1 y1
x2 y2
x6 y6
y
y22 C
12 12 12 1
2
y6
2
1
N e x, y P x, y C 1

5.

Явный способ построения функций форм треугольных элементов
n
Ni
1 F
F
где n – порядок аппроксимации; F – функции L-координат L1 , L2 , L3 , определяется из
L ,L ,L
1 2 3
уравнений n линий, которые проходят через все узлы за исключением i -го узла, для которого
определяется функция формы.
L1 const, F1 L1 C
Функции формы для кубического элемента
F1 L1 0
F1 L1 0
F1 1, 0,0 1
1
3
2
F3 L1
3
F2 1, 0, 0
F2 L2 0
F3 1,0, 0
F3 L3 0
F2 L1
2
3
1
3
1
2
L1
L1
L 0
3
3 L1 3L 1 3L 2
N1 1
1
1
2
1
1
2
3
3
F1 L1 0
F1
1
F2 L1
3
F2
F3 L2 0
F3
L 0
N2 1
2
3
2 1
, ,0
3 3
2 1
, ,0
3 3
2 1
, ,0
3 3
2
3
1
3
1
3
1
3 L2 0 9 L L 3L 1
1 2
1
1
1
2
3
3
L1
N 10
1
3
333
1
F2 1 , 1 , 1
3
333
1
F3 1 , 1 , 1
3
333
F1 1 , 1 , 1
L1 L2 L3
27 L1 L2 L3
1 1 1
3 3 3

6.

L1
3L1 1 3L1 2
2
9
N 2 L1 L2 3L1 1
2
9
N 3 L1 L2 3L2 1
2
L2
3L2 1 3L2 2
N4
2
9
N 5 L2 L3 3L2 1
2
9
N 6 L2 L3 3L3 1
2
L
N 7 3 3L3 1 3L3 2
2
9
N 8 L3 L1 3L3 1
2
9
N 9 L3 L1 3L1 1
2
N 10 27 L1 L2 L3
N1
Таким образом, у таких конечных элементов первые
производные от функции формы не постоянны, следует,
напряжения и деформации изменяются в пределах конечного
элемента, но несогласованны между конечными элементами
(поля упорядоченных деформаций и напряжений будет с
разрывами по границам элемента).
«+»
1. Требуется меньшее число нелинейных
треугольников для получения той же точности, что и в
симплекс-элементе.
2.
Возможно
построение
элементов
с
криволинейными границами.
3.
Для вычисление матрицы жесткости
и
векторов узловых сил удобно применять численное
интегрирование.
«–»
1. Так как больше узлов, значит больше координат.
2. Более громоздки процедуры.

7.

Треугольный конечный элемент с эрмитовой аппроксимацией перемещений
y
vi
v
x i
v
y i
i
2
2
3
2
2
3
U ( x, y) 1 2 x 3 y 4 x 5 xy 6 y 7 x 8 x y 9 xy 10 y ,
2
2
3
2
2
3
V ( x, y ) 11 12 x 13 y 14 x 15 xy 16 y 17 x 18 x y 19 xy 20 y .
k
vm
m
um
u u
ui
x i y i
j
Ui
U
i
x i
U
i
y
i
i
V
i
V
i
x i
V
i
x
y i
e
i
j
k
U
m
V
m
f
U
U
y
... N m ( x, y )U m
U ( x, y ) N i 0 ( x, y )U i N i x ( x, y )
N i ( x, y )
x
y
i
i
N (0) L 3L 2 L2 7 L L ,
1
1
1
2 3
i
N ( x ) L c L L L c L L L ,
i
1 3 2 1
3
2 3 2
1
i, j , k
N ( y ) L b L L L b L L L ,
1 3 2
3
1
2 3 1
2
i
N m 27 L1L2 L3 ,
U ( x, y )
e
e
N ( x, y )
V ( x, y )

8.

N i( x ) U N i( y )
U ( x, y ) N i( 0 )
Ui
x
x
x x i
x
N m
U
...
Um
x
y i
N i( x )
U ( x, y ) N i( 0 )
Ui
y
y
y
N m
U
...
Um
y
y
i
( y)
U N i
x
y
i
Требования
Проверка
(0)
(0)
(0)
Ni(0) ( x j , y j ) ij , N i( x ) ( x j , y j ) N i( y ) ( x j , y j ) 0, Ni ( x j , y j ) Ni ( xk , yk ) 0, Ni ( xi , yi ) 1(3 2) 1,
1 2 7
Ni(0) ( xm , ym ) 1 0,
3 9 9
N m ( x j , y j ) mj ,
Ni( x ) ( x j , y j )
x
Ni(0) ( x j , y j )
x
N (j x ) ( x j , y j )
y
Ni(0) ( x j , y j )
y
«+»
ij ,
x
N m ( x j , y j )
x
0,
N i( y ) ( x j , y j )
y
y
0,
Ni( y ) ( x j , y j )
N m ( x j , y j )
0,
3b
Ni(0)
b
4 L b 7 Lk b j 7 L j bk
i e 3Li 2 L2i 7 L j Lk Li ie i ei
x
2A
2A
2 Ae
2 Ae
2A
ij ,
bi
e
2A
3Li 2L2i 7 L j Lk 2LAi e 3bi 4Libi 7 Lk b j 7 L jbk ,
Ni(0) ( xi , yi )
b
1
i e 3 2 e 3bi 4bi 0,
x
2A
2A
Ni(0) ( x j , y j )
x
0 0 0.
0.
1. так как высокий порядок аппроксимации, требуется малое количество
элементов для получения решения с той же точностью, что и у симплексэлемента;
2. из решения получаются согласованные в узлах сетки значения и ;
3. непосредственно из решения получаются значения на границе.