Похожие презентации:
Равнодействующие силы в пространстве. (Лекция 3)
1. Лекция № 3
2. ПЛАН
1) Возможные случаи приведения кравнодействующей сил произвольно разложенных в
пространстве.
2) Условие равновесия пространственной системы
сил.
3) Инварианты системы сил.
4) Условие равновесия системы сходящихся сил в
векторной форме. Аналитические условия
равновесия системы сходящихся сил.
5) Теорема о равновесии трех непараллельных сил.
Понятие о статике определимых и неопределимых
задачах.
6) Сложение трёх сил, не лежащих в одной
плоскости.
3. 1. Возможные случаи приведения к равнодействующей сил произвольно разложенных в пространстве.
По инвариантам статики можно судить о возможных частных случаяхприведения исходных системы сил.
I)
R 0, M 0 0
Система сил приводится к одной силе – равнодействующей, при этом линия
действия равнодействующей проходит через центр приведения.
II)
R 0, M 0 0.
Исходную систему сил можно заменить двумя силами, образующими пару сил.
III)
а)
R 0, M 0 0.
сил приводится
Система
к силе и паре.
R M 0 0 ,то есть R M 0 - пара и сила лежат в одной плоскости.
Выбирая силы, составляющие пару
находим ее плечо h R
M0 ;
h
M0
.
R
4.
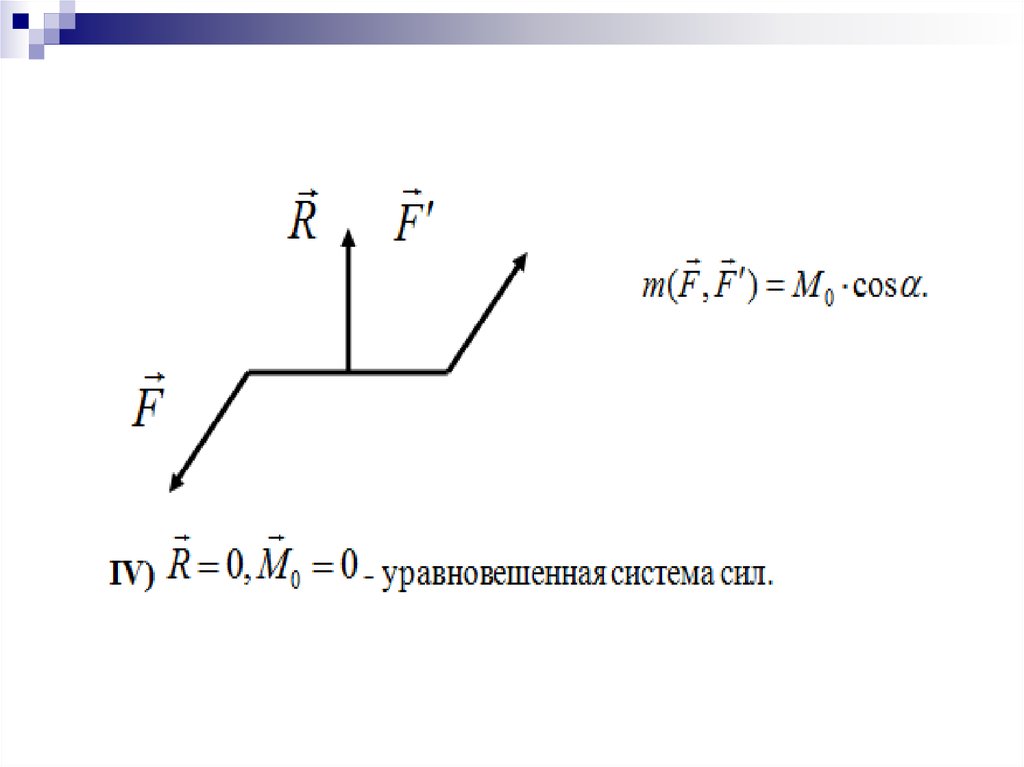
Силы R,R" образуютуравновешенную систему сил. В
результате исходная система сил
приводится
к равнодействующей
{ R, R , R }~{ R }, которая проходит
через т. О , отстоящую от центра
приведения на расстоянии, равном
отношению главного момента к
главному вектору.
Этот случай всегда реализуется у
плоской системы сил при отличных от
нуля главном векторе и главном
моменте.
5.
б) R M 0плоскости.
0 - система сил приводится к силе и паре, не лежащих в одной
6.
7. 2. Условие равновесия пространственной системы сил.
Произвольной пространственной системой сил называется системасил линии действия которых не лежат в одной плоскости.
Согласно основной теоремы статики (теореме Пуансо), любую
произвольную систему сил, действующих на твердое тело, можно
заменить эквивалентной системой, состоящей из силы (главного
вектора системы) и пары сил (главного момента сил).
Отсюда вытекает условие равновесия произвольной
пространственной системы сил:
В геометрической форме: для равновесия произвольной
пространственной системы сил необходимо и достаточно, чтобы
главный вектор и главный момент системы равнялись нулю.
R 0, M 0 0.
8.
В аналитической форме: для равновесия произвольнойпространственной системы сил необходимо и достаточно, чтобы суммы
проекций всех сил на три координатные оси и суммы моментов всех сил
относительно этих осей были равны нулю.
9. 3. Инварианты системы сил.
Физические величины инвариантны относительно данногопреобразования координат, если значения этих величин не меняются
при переходе к другой системе координат.
Главный вектор для любого центра приведения выражается векторной
суммой:
R Fi
Таким образом, главный вектор системы сил является векторным
инвариантом. Для одной и той же системы сил он не зависит от выбора
центра приведения.
Получим второй скалярный инвариант. Для этого умножим правую и
левую части уравнения (3.1) скалярно на
(3.1)
: M M 00 R
R
01
M 01 R M 0 R (001 R) R
0
1
получим:
(3.2)
Т.к. смешанное произведение векторов, содержащих два одинаковых
множителя R, равно нулю, т.е
( R 00) R 0.
10.
Из формулы (3.2) видно, скалярное произведение главного момента наглавный вектор не зависит от центра приведения, т.е. является вторым
скалярным инвариантом.
M R cos M R cos
01
где
1
1
M 01 и R
- угол между
векторами
- угол между M 0
и
0
R . После сокращения на
M 01 cos 1 M 0 cos (3.3).
R
Проекция главного момента на линию действия главного вектора не
зависит от центра приведения.
Разложим главный момент в каждом центре приведения на две взаимно
перпендикулярные
составляющие, одна из которых направлена по главному
вектору R (рис.). Учитывая, что главные векторы в различных центрах
приведения согласно (3.3) равны, получим:
M 0 M 01.
11. 4. Условие равновесия системы сходящихся сил.
Пусть на абсолютно твердое тело действует система сходящихся сил. Тогдадля равновесия этой системы сил необходимо и достаточно,
чтобы
равнодействующая системы R была равна нулю, т.е. R
Fi 0 (3.4) - это
условие равновесия в векторной форме.
В проекциях на оси декартовых координат условие равновесия представляют
так:
т.е. для равновесия системы сходящихся сил необходимо и достаточно,
чтобы сумма проекций всех сил на каждую из осей координат была равна
нулю. Для плоской системы сил в проекциях будут только два условия
равновесия.
Геометрическое условие равновесия (3.5) означает следующее: поскольку
для равновесия системы сходящихся сил необходимо и достаточно, чтобы
равнодействующая равнялась нулю, то необходимо и достаточно, чтобы
векторный многоугольник, построенный на этих силах, как на сторонах, был
замкнут.
12.
13. 5. Теорема о равновесии трех непараллельных сил. Понятие о статике определимых и неопределимых задачах.
Теорема о равновесии трех непараллельных сил.14.
Понятие о статике определимых и неопределимых задачах.Для любой плоской системы сил, действующих на твердое тело,
имеется только три независимых условия равновесия, каждые из
которых не является следствием двух других.
Независимые условия равновесия можно брать в трех различных
формах. В случае пространственной системы сил, действующих на
твердое тело, имеется шесть независимых условий равновесия.
Следовательно, для любой пространственной системы сил из условий
равновесия можно найти не более 6 неизвестных.
Задачи, в которых число неизвестных не больше числа
неизвестных условий равновесия для данной системы сил,
приложенных к твердому телу, называется статистически
определимыми.
В противном случае задачи статистически неопределимы.
Если система трех непараллельных сил находится в равновесии,
то линии действия этих сил должны пересекаться в одной точке.














 Физика
Физика








