Елементи комбінаторики

1.

Елементи комбінаторики
1. Правило суми і добутку
Стислі теоретичні відомості
Правило суми
Класичне
формулювання
Якщо якийсь елемент множини A можна вибрати n способами, а елемент множини B — m способами, то вибір
елемента із множини A або
із множини B можна зробити
n + m спосо­бами.
Формулювання в термінах
теорії множин
Якщо множина A складається з n елементів, а множина B — з m елементів, то ви­
брати елемент із множини A
або із множини B можна n + m
способами.
Приклад. У коробці 5 кольорових олівців і 7 фломастерів.
Скількома способами можна вибрати один олівець або один фло­
мастер?
Розв’язання
I способ
II способ
Один олівець із 5 можна вибра- Множина олівців складаєтьти 5 способами, а один флома­
ся з 5 елементів, а множина
стер — 7 способами. За правифломастерів — із 7 елементів.
лом суми один предмет можна
Вибрати предмет із множини
вибрати 5 + 7 = 12 спо­собами.
олівців або із множини флома­
стерів можна 12 способами.
Правило добутку
Класичне
формулювання
Якщо якийсь елемент множини A можна вибрати n способами, після кожного такого
ви­бору елемент із множини
B — m способами, то пару елементів із множин A і B можна
вибрати m ⋅ n ­способами.
Формулювання в термінах
теорії множин
Нехай є дві множини: A = {a1 , a2 , ..., an }
і B = {b1 , b2 , ..., bm } . Парою називається об’єкт вигляду ai , bj ,
де i = 1, …, n , j = 1, …, m .
(
14
)

2.

Елементи комбінаторики
Зрозуміло, що в таких задачах
порядок розташування елементів не важливий.
Якщо множина A складається з n елементів, а множина
B — із m елементів, то можна скласти рівно n ⋅ m пар
( )
що ( a , b ) = ( b , a ) , i = 1, …, n ,
ви­гляду ai , bj , вважаючи,
i
j
j
i
j = 1, …, m .
Приклад. У коробці є 5 олівців і 7 фломастерів. Скількома способами можна вибрати пару, яка складається із одного олівця і одного фломастера?
Розв’язання
I способ
Із першої коробки один олівець
можна вибрати 5 способами
і кожному вибраному олівцю
можна взяти до пари будьякий із 7 фломастерів. Отже,
за правилом добутку маємо
5 ⋅7 = 35 способів.
II способ
Множина олівців складається із 5 елементів, а множина
фломастерів — із 7 елементів.
За правилом добутку скласти
пару із одного олівця і одного
фломастера можна 5 ⋅7 = 35
способами.
Наслідок із правила добутку
Якщо якийсь елемент множини A1 можна вибрати n1 способами, після цього елемент
із множини A2 можна вибрати
n2 способами, ..., елемент
із множини Ak −− nk способами, то групу елементів, яка
складається з одного елемента
множини A1 , одного елемента
множини A2 , ..., одного елемента множини Ak , можна
скласти n1 ⋅ n2 ⋅…⋅ nk способами.
Якщо множина A1 складається з n1 елементів, множина A2 — із n2 елементів, ...,
множина Ak — із nk елементів, то число груп вигляду
(ai1 , ai2 , ..., aik ) , де a1 ∈ A1 ,
a2 ∈ A2 , ..., ak ∈ Ak ,
дорівнює n1 ⋅ n2 ⋅ n3 ⋅…⋅ nk .
15

3.

Елементи комбінаторики
Приклад. У коробці 5 олівців, 7 фломастерів і 10 листівок.
Скількома способами можна скласти із одного олівця, одного фломастера і однієї ли­стівки подарунок для першокласника?
Розв’язання
I способ
II способ
Один олівець можна вибрати
Множина олівців складається
5 способами, кожному обраіз 5 елементів, множина флома­
ному олівцю до пари можна
стерів — із 7, множина листі7 способами вибрати флома­
вок — із 10 елементів. Складатистер, кожній парі одну листівку мемо різні «трійки», у яких один
можна дібрати 10 способами.
предмет — із множини олівців,
Разом маємо 5 ⋅7 ⋅10 = 350 сподругий — із множини фломассобів.
терів, а третій — із множини
листівок. За правилом добутку
це можна зробити 5 ⋅7 ⋅10 = 350
способами.
Приклади розв’язування задач
Приклад 1. У групі 10 дівчаток і 15 хлопчиків.
Скількома способами із цієї групи можна вибрати:
а) одного хлопчика;
б) одного хлопчика або одну дівчинку;
в) одного хлопчика і одну дівчинку?
Розв’язання
а) Із 15 хлопчиків одного можна вибрати 15 способами;
б) за правилом суми дівчинку або хлопчика можна вибрати
10 + 15 = 25 способами;
в) за правилом добутку пари «дівчинка і хлопчик» можна ви­
брати 10 ⋅15 = 150 способами.
Відповідь: а) 15; б) 25; в) 150.
Приклад 2. У країні Чудес є три міста — А, Б і В. Із міста А
до міста Б веде 6 доріг, а з міста Б до міста В — 4 дороги. Скількома
способами можна проїхати з міста А до міста В?
Розв’язання. З А до В можна дістатися, пройшовши 2 частини
шляху: з А до Б, що можна здійснити 6 способами, і з Б до В, що
можливо зробити 4 способами. Скласти пари доріг: з А до Б й із Б
до В можна 6 ⋅ 4 = 24 способами.
Відповідь: 24.
16

4.

Елементи комбінаторики
Приклад 3. У країні Чудес (див. приклад 2) побудували ще одне
місто — Г і нові дороги: з А до Г — 2 дороги, із Г до В — 3 дороги.
Скількома способами тепер можна дістатися з А до В?
Розв’язання. Щоб дістатися з А до В, існує два варіанти: через
місто Б, що можна зробити 6 ⋅ 4 = 24 способами, або через місто Г, що
можливо здійснити 2 ⋅ 3 = 6 способами.
За правилом суми всього способів 24 + 6 = 30 .
Відповідь: 30.
Приклад 4. Скількома способами можна вибрати одну голосну
й одну приголосну зі слова: а) «цукат»; б) «телефон»?
Розв’язання
а) Множина голосних букв слова «цукат» складається з двох
букв {у, а } ; множина приголосних — із трьох: {ц, к, т} .
Складаючи різні пари цих множин, одержимо 2 ⋅ 3 = 6 способів;
б) множина голосних: {е, о} , приголосних: {т, л, ф, н} .
Разом: 2 ⋅ 4 = 8 способів.
Відповідь: 8.
Приклад 5. Складають автомобільні номери, що містять чотири
цифри. Скільки таких номерів можна скласти, якщо:
а) використовувати 10 цифр;
б) використовувати тільки непарні цифри?
Розв’язання
а)
I способ
II способ
Першу цифру можемо вибрати Складатимемо різні «четвір10 способами, після чого друки» цифр, кожну з яких вибигу — так само 10 способами,
раємо з 10-елементної мнопотім третю і четверту — теж
жини. За правилом добутку
10 способами. Усього маємо
маємо 10 ⋅10 ⋅10 ⋅10 = 104 но4
10 ⋅10 ⋅10 ⋅10 = 10 способів.
мерів.
б) Аналогічно маємо 54 = 625 способів.
Відповідь: а) 104 ; б) 625.
Приклад 6. Скількома способами із 5 конвертів, 4 марок і 6 листівок можна вибрати два предмети з різними назвами?
Розв’язання. Марку і конверт можна вибрати 5 ⋅ 4 = 20 способами, марку і листівку — 4 ⋅ 6 = 24 способами, конверт і листівку —
5 ⋅ 6 = 30 способами. Одну пару — або другу, або третю — за правилом суми можна вибрати 20 + 24 + 30 = 74 способами.
Відповідь: 74.
17

5.

Елементи комбінаторики
Приклад 7. Монету кидають тричі. Скільки різних послідовно­
стей орлів або решок можна при цьому одержати?
Розв’язання. Складатимемо різні «трійки» результатів підкидання монети. Кожний елемент цієї «трійки» вибираємо із двох­
елементної множини {орел, решка}. За правилом множення маємо
2 ⋅ 2 ⋅ 2 = 23 = 8 послідовностей.
Відповідь: 8.
Приклад 8. Підкидають одночасно два гральні кубики. Скільки
різних варіантів випадання цифр може при цьому вийти?
Розв’язання. Для кожної із шести цифр першого кубика можлива будь-яка із шести цифр другого кубика. За правилом добутку
маємо 6 ⋅ 6 = 36 варіантів.
Відповідь: 36.
Приклад 9. Алфавіт племені мумбо-юмбо складається з трьох
літер: м, ю, б. «Словом» є будь-яка послідовність, що складається
не більше ніж із 4 літер. Скільки «слів» у мові племені мумбо-юмбо?
Розв’язання. «Не більше ніж» означає, що «слово» може
бути одно-, двох-, трьох- і чотирьохлітерним. «Слів», що складаються з однієї літери,— 3, із двох літер — 3 ⋅ 3 = 9 , із трьох —
3 ⋅ 3 ⋅ 3 = 27 , із чотирьох — 34 = 81 . Кількість усіх «слів» становить
3 + 9 + 27 + 81 = 120 .
Відповідь: 120.
Приклад 10. На фермі є 20 овець і 24 свині. Скількома способами можна вибрати одну вівцю й одну свиню? Якщо такий вибір уже
зроблено, скількома способами його можна зробити ще раз?
Розв’язання. Перша частина задачі розв’язується просто — 20 ⋅ 24 = 480 способів. Після першого вибору залишилося
19 овець і 23 свині, і тепер аналогічний вибір можна зробити 19 ⋅ 23 = 437
19 ⋅ 23 = 437 способами.
Відповідь: 437.
Приклад 11. У прикладі 10 вибрали одну тварину. Скількома способами після цього можна вибрати одну вівцю й одну свиню?
Розв’язання. У першому випадку могли вибрати або вівцю, або
свиню. Якщо вибрали вівцю, що можна зробити 20 способами, то
із решти тварин пару можна вибрати 19 ⋅ 24 = 456 способами. Якщо
ж спочатку вибрали свиню, то після цього пару можна вибрати
20 ⋅ 23 = 460 способами. Усього маємо 456 + 460 = 916 способів.
Відповідь: 916.
18

6.

Елементи комбінаторики
Задачі для самостійного розв’язування
1. У букеті 10 троянд і 12 хризантем. Скількома способами
можна вибрати із букета:
а) або одну троянду, або одну хризантему;
б) одну троянду або одну хризантему;
в) одну троянду й одну хризантему?
2. У магазині посуду є 5 видів чашок і 7 видів блюдець. Скількома способами можна вибрати пару блюдець і чашку?
3. У магазині посуду із задачі 2 є ще 6 видів чайних ложок.
Скільки існує способів скласти набір із чашки, блюдця і ложки?
4. У глядацькому залі кінотеатру всього 6 дверей. Скільки
­існує способів:
а) увійти до глядацького залу і вийти з нього;
б) увійти до залу і вийти, але так, щоб вхід і вихід здійснювалися через різні двері?
5. У глядацькому залі із задачі 4 існує ще двоє дверей до кімнати кіномеханіка. Скількома способами кіномеханік може потрапити на робоче місце?
6. У класі 30 учнів. Щодня призначається один черговий.
Скількома способами можна скласти графік чергування на 5 днів
так, щоб ніхто не чергував більше одного разу?
7. Скільки існує різних телефонних номерів, якщо вважати,
що кожний номер складається із 7 цифр (телефонний номер може
починатися з нуля)? Як зміниться розв’язок задачі, якщо телефонні номери можуть бути як семи-, так і шестицифровими?
8. Кидають дві монети. Скільки різних варіантів випадання
«орел — решка» може при цьому вийти?
9. Гральний кубик кидають тричі. Скільки різних послідовностей чисел може при цьому вийти?
10. Кожна літера азбуки Морзе — це послідовність крапок
і тире. Скільки різних слів можна скласти, якщо використовувати
для кожного з них:
а) 5 символів;
б)  не більше ніж 5 символів?
11. Скількома способами можна вказати на шахівниці:
а) два білих квадрати;
б) білий і чорний квадрати, якщо вони не лежать на одній горизонталі або одній вертикалі?
19

7.

Елементи комбінаторики
12. У кошику 10 яблук і 12 апельсинів. Іван вибирає або яблуко,
або апельсин, після чого Надя вибирає із фруктів, що залишилися,
апельсин. Скільки можливостей такого вибору?
13. Скільки можна скласти із цифр 0, 1, 2, 3, 4, 5:
а) різних трицифрових чисел;
б) різних трицифрових чисел, якщо цифри в них не повторюються;
в) різних трицифрових чисел, що діляться на 5?
14. Чотири учні одержують оцінки 2, 3, 4, 5.
а) Скількома способами можна поставити їм оцінки?
б) Скількома способами можна поставити оцінки так, щоб
жодні два учні не одержали однакових?
в) Скількома способами можна поставити оцінки так, щоб усі
одержали 4 або 5?
20

8.

Елементи комбінаторики
2. Розміщення
Стислі теоретичні відомості
Поняття факторіала
•• Факторіалом натурального числа n називається добуток усіх натуральних чисел від 1 до n. Позначення: n ! = n ⋅ (n − 1) (n − 2) ⋅…⋅ 2 ⋅1 .
Наприклад, 6 ! = 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅1 = 720 . Очевидно, що n ! = n ⋅ (n − 1) ! .
Прийнято, що 0 ! = 1 .
Із визначення:
1! = 1 ;
2! = 2 ;
3! = 6 ;
4 ! = 24 ;
5 ! = 120 ;
6 ! = 720
і т. д.
Приклади
а)
б)
в)
г)
д)
6!
=
5!
10 !
7!
6 ⋅5 !
=
5!
=6.
1 ⋅ 2 ⋅ 3 ⋅ 4 ⋅ 5 ⋅ 6 ⋅ 7 ⋅ 8 ⋅ 9 ⋅ 10
1⋅ 2 ⋅ 3 ⋅ 4 ⋅ 5 ⋅ 6 ⋅7
= 8 ⋅ 9 ⋅10 = 720 ;
20 ! 18 ! ⋅ 19 ⋅ 20
= 19 ⋅ 20 = 380
=
;
18 !
18 !
18 !
20 !
n!
( n − 1) !
=
n ⋅ ( n − 1) !
( n − 1) !
=n ;
( n + 1) ! = ( n + 1) n ( n − 1) ! = n n + 1 .
( )
( n − 1) !
( n − 1) !
21

9.

Елементи комбінаторики
Розміщення
•• Нехай дано множину A = {a1 , a2 , …, an } .
Кожну її впорядковану підмножину, що складається із m різних елементів, називають розміщенням із n елементів по m елементів.
Позначення: Anm .
Читають: «розміщення з n елементів по m елементів» або «число
розміщень із n елементів по m елементів».
Число розміщень із n елементів по m обчислюють за фор­
мулами
Anm = n (n − 1) (n − 2) ⋅ … ⋅ (n − m + 1) ;
Anm =
n!
(n − m) !
.
(1)
(2)
Формула (1) застосовується у випадку, якщо можна знайти
результат, а формула (2) — якщо результат важко обчислити через великі числа або у випадку використання в задачі літерних
­змінних.
Приклад. У коробці 7 кольорових олівців. Складатимемо різні впорядковані підмножини із 3 олівців, причому будь-які дві
підмножини, що відрізняються порядком черги олівців, вважаємо
різними. Такий вибір і є розміщенням із 7 елементів по 3, і таких
можливостей вибору буде A73 = 7 ⋅ 6 ⋅ 5 = 210 .
(Очевидно, що у цій задачі застосовується формула (1).)
Приклади розв’язування задач
Приклад 1. У класі 30 учнів. Скількома способами можна в ньому вибрати старосту і його заступника?
Розв’язання. Тут важливо, хто із двох обраних буде старостою, а хто — його заступником, тобто важливий порядок. Маємо
розміщення із 30 по 2.
2
A30
= 30 ⋅ 29 = 870 способів.
Відповідь: 870.
22

10.

Елементи комбінаторики
Приклад 2. Прапор складається із 4 горизонтальних смуг різного кольору.
а) Скільки таких прапорів можна одержати, маючи у своєму
розпорядженні смуги 7 кольорів (перестановки будь-яких
двох кольорів дають новий прапор)?
б) Скільки таких прапорів можна одержати зі смуг 7 кольорів,
якщо в усіх прапорів нижня смуга має бути однакового кольору?
Розв’язання
а) A74 = 7 ⋅ 6 ⋅ 5 ⋅ 4 = 840 прапорів;
б) розв’язання зводиться до складання триколірних прапорів,
причому кількість кольорів зменшилася до шести. Маємо
A63 = 6 ⋅ 5 ⋅ 4 = 120 прапорів.
Відповідь: а) 840; б) 120.
Приклад 3. У чемпіонаті країни з футболу беруть участь 16 команд. Скількома способами можна скласти трійку призерів?
Розв’язання. Оскільки на одному місці може опинитися тільки одна із команд, то маємо
3
A16
= 16 ⋅15 ⋅14 = 5360 .
Відповідь: 5360.
Приклад 4.
а) Чемпіонат країни з футболу, в якому беруть участь 16 команд, проводиться у два кола (кожна команда двічі зустрічається з кожною з інших). Яка кількість зустрічей буде
в чемпіонаті?
б) Скільки буде зустрічей, якщо чемпіонат проводитиметься
в одне коло?
Розв’язання
а) У кожній зустрічі одну з команд назвемо «гостем», а другу — «хазяїном». Очевидно, кількість зустрічей дорівнює
кількості впорядкованих пар «хазяїн — гість», «гість — хазяїн», що обираються із 16 команд.
2
Усього A16
= 16 ⋅15 = 240 зустрічей;
б) у чемпіонаті в одне коло нам потрібні тільки пари «хазяїн —
гість». Тобто кількість зустрічей буде у два рази менша. Ра2
зом A16
⋅
1
2
= 120 зустрічей.
Відповідь: а) 240; б) 120.
23

11.

Елементи комбінаторики
Приклад 5. Команда із трьох членів виступає на змаганнях,
у яких беруть участь ще 15 спортсменів. Скількома способами можуть бути розподілені місця, що посіли члени цієї команди, за умови, що жодне місце не може бути поділене?
Розв’язання. Усього в змаганнях беруть участь 18 спортсменів.
Будемо з 18 наявних місць вибирати 3 для членів даної команди.
3
A18
= 18 ⋅17 ⋅16 = 4896 .
Відповідь: 4896.
Приклад 6. Якою буде кількість способів розподілу місць у попередній задачі, якщо відомо, що жоден із членів даної команди
не посів місце нижче десятого?
Розв’язання. Вибираємо три місця із десяти, що залишилися.
3
A10
= 10 ⋅ 9 ⋅ 8 = 720 .
Відповідь: 720.
Приклад 7. Скільки різних трицифрових натуральних чисел
можна скласти із запропонованого набору цифр за умови, що жодна
цифра в кожному із цих чисел не повторюється?
а) 1, 2, 3, 4, 5;
б)  0, 1, 2, 3, 4.
Розв’язання
а) Із п’ятиелементної множини складатимемо різні трьохелементні підмножини.
A53 = 5 ⋅ 4 ⋅ 3 = 60 ;
б) усього трицифрових чисел буде A53 = 60 , але нас не задовольняють числа, які починаються з нуля, таких чисел буде A42
(до першої цифри «0» приєднуватимемо різні двохелементні
підмножини, які складаються з чотирьох цифр, що залишилися). Разом: A53 − A42 = 60 − 12 = 48 чисел.
Відповідь: а) 60; б) 48.
Приклад 8. Скільки різних натуральних чисел, які містять не
більше ніж три знаки, можна скласти з цифр 2, 4, 6, 8?
Розв’язання. «Не більше ніж» означає, що числа можуть
бути одно-, або дво-, або трицифровими. За правилом суми маємо
A41 + A42 + A43 = 4 + 4 ⋅ 3 + 4 ⋅ 3 ⋅ 2 = 4 + 12 + 24 = 40 чисел.
Відповідь: 40.
Приклад 9. Скільки різних натуральних чисел можна скласти
із цифр 0, 1, 2, 3, щоб до кожного такого числа кожна із цих цифр
входила не більше одного разу?
24

12.

Елементи комбінаторики
Розв’язання. Ми вже розв’язували схожу задачу (див. приклад 7, б), проте тепер складемо одно-, дво-, три- і чотирицифрові
числа. Одноцифрових: A31 ; двоцифрових — A42 − A31 ; трицифрових — A43 − A32 ; чотирицифрових — A44 − A31 .
Усього чисел — A31 + A42 − A31 + A43 − A32 + A44 − A33 = 48 .
Відповідь: 48.
Приклад 10. (Узагальнена задача.) Скільки є різних упорядкованих підмножин множини, що складається з n елементів?
Відповідь: An1 + An2 + An3 + … + Ann .
Задачі для самостійного розв’язування
1. У команді 12 членів. Скількома способами можна вибрати
в ній капітана і воротаря?
2. Скільки словників треба видати, щоб можна було безпосередньо виконувати переклади з кожної із п’яти мов: російської,
англій­ської, французької, німецької та іспанської на будь-яку іншу
з цих мов?
3. Розклад одного дня містить 5 уроків. Визначте кількість таких розкладів при виборі з 11 предметів і за умови, що один предмет
займає один урок. Як зміниться розв’язування задачі, якщо відомо,
що першим уроком обов’язково має бути математика?
4. Скількома способами можна вибрати з повної колоди карт
(52 шт.) по одній карті кожної масті за умови, що серед вийнятих карт немає жодної пари однакових, тобто двох королів, двох
дам і т. д.?
5. Скільки різних дробів, що не дорівнюють одиниці, можна
скласти з чисел 3, 5, 7, 11, 13, 17, 19, 23 так, щоб до кожного дробу
входило два числа? Скільки серед них буде правильних?
6. Чотири біатлоністи з України брали участь у чемпіонаті світу. Скількома способами могли бути розподілені місця, які посіли
представники України, якщо:
а) жоден із них не посів місце нижче п’ятнадцятого, і жодне
місце не було поділено;
б) жоден із них не посів призового місця, а всього було 15 учасників чемпіонату?
25

13.

Елементи комбінаторики
7. Скільки різних чотирицифрових натуральних чисел можна
скласти із цифр:
а) 2, 3, 5, 7, 9;
б) 0, 2, 3, 5, 7, 9?
8. Скільки різних чотирицифрових парних чисел можна скласти із цифр:
а) 1, 3, 5, 7, 8;
б) 2, 4, 6, 8, 9?
9. Людина має 10 друзів і протягом декількох днів запрошує
двох із них у гості так, що кожен побував у неї в гостях тільки один
раз. Скільки різних варіантів зустрічей вона може скласти?
10. Людина має 10 друзів і щодня запрошує декількох із них
у гості (або одного), але в різний час. Скільки варіантів прийому гостей вона може скласти, якщо жодні групи гостей не повторюються?
11. Скільки різних натуральних чисел можна скласти із цифр
1, 2, 3, 4?
26

14.

Елементи комбінаторики
3. Перестановки
Стислі теоретичні відомості
•• Перестановкою із n елементів називається будь-яка впорядкована множина з усіх цих елементів, причому дві такі множини
вважаються різними, якщо вони відрізняються між собою порядком елементів.
Позначення: Pn .
Читають: кількість перестановок із n елементів.
Зрозуміло, що кількість перестановок із n елементів — це число розміщень із n елементів по n елементів, тобто вибір різних
n-елеметних підмножин із n-елементної множини, кожні дві з яких
відрізняються порядком елементів.
Pn = Ann =
n!
(n − n) !
=
n!
0!
=
n!
1
= n!
Приклад. Скількома способами можна розставити в шеренгу
10 людей?
Розв’язання. Маємо різні перестановки з 10 елементів:
P10 = 10 !
Приклади розв’язування задач
Приклад 1. Скількома способами можна розставити на полиці
5 книг?
Відповідь: P5 = 5 !
Приклад 2. Скільки нових «слів» можна скласти з букв слова:
а) «цукат»;
б)  «ручник»?
Відповідь: а) P5 = 5 ! ; б) P6 = 6 !
Приклад 3. Скільки чотирицифрових чисел можна скласти із запропонованого набору цифр, не повторюючи їх?
а) 1, 2, 3, 4;
б)  0, 1, 2, 3.
Розв’язання
а) P4 = 4 ! = 24 ;
б) від усіх чотирицифрових чисел віднімемо ті, які починаються з нуля:
P4 − P3 = 4 !− 3 ! = 18 .
Відповідь: а) 24; б) 18.
27

15.

Елементи комбінаторики
Приклад 4. Скількома способами можна розставити 5 томів
зібрання творів О. С. Пушкіна так, щоб:
а) перший том стояв ліворуч;
б) перший том стояв зкраю;
в) перший і другий томи стояли поруч;
г) перший і другий томи стояли ліворуч;
д) перший і другий томи не стояли поруч?
Розв’язання
а) Якщо перший том стоїть ліворуч, то переставляти будемо
чотири, що залишилися: P4 = 4 ! = 24 ;
б) перший том може стояти ліворуч або праворуч. За правилом
суми маємо: P4 + P4 = 48 ;
в) об’єднаємо перший і другий томи в один. Тоді переставляти
будемо 5 − 2 + 1 = 4 книги (див. рисунок) P4 способами, при
цьому перший і другий томи можна переставляти P2 способами. За правилом добутку маємо: P4 ⋅ P2 = 4 !⋅ 2 ! = 48 ;
1
2
г) перший і другий томи, об’єднані в один, будемо переставляти між собою P2 способами, але в загальній перестановці
трьох книг, що залишилися, вони участі не братимуть. Таким чином маємо: P3 ⋅ P2 = 3 !⋅ 2 ! = 12 ;
д) з усіх перестановок п’яти книг виключимо ті, у яких перший і другий томи стоять поруч.
Тоді одержимо P5 − P4 ⋅ P2 = 120 − 48 = 72 .
Відповідь: а) 24; б) 48; в) 48; г) 12; д) 72.
Приклад 5. На танцмайданчику зібралися N юнаків і N дівчат.
Скількома способами вони можуть розбитися на пари для участі
в черговому танці?
Розв’язання
I спосіб: поставимо в шеренгу один навпроти одного дівчат і юнаків. Переставлятимемо тільки юнаків. Тоді кожен юнак опиниться
напроти кожної дівчини. Таким чином, маємо PN = N ! способів.
II способ: у танцювальний зал заходить юнак — перед ним N
дівчат, із яких він обирає одну, потім другий юнак — йому для ви­
бору залишилася N −1 дівчина, третьому — N − 2 і т. д. За правилом добутку маємо N ( N − 1) ( N − 2) … 2 ⋅1 = N ! .
Відповідь: N !
28

16.

Елементи комбінаторики
Приклад 6. Скількома способами можна пошикувати в одну шеренгу гравців двох футбольних команд (по 11 чоловік) так, щоб при
цьому два футболісти однієї команди не стояли поруч?
Розв’язання. Футболістів однієї команди розставимо P11
способами. Між ними розставимо футболістів другої команди
P11 спосо­бами. При цьому першим стоятиме футболіст першої команди. Потім виконаємо ті самі перестановки, але з урахуванням
того, що першим тепер стоятиме футболіст другої команди. Тоді
2
маємо 11 ! ⋅11 !+ 11 ! ⋅11 ! = 2 ⋅ (11 ! ) .
Відповідь: 2 ⋅ (11 ! ) .
2
Приклад 7. Скільки різних кілець, що світяться, можна утворити, розмістивши по колу 10 різнокольорових лампочок (кільця
вважаються однаковими, якщо порядок розміщення кольорів той
самий)?
Розв’язання. Оскільки лампочки розміщені по колу, то кожне розміщення, яке відрізняється порядком розміщення кольорів,
має ще 9 таких самих, утворених поворотом кільця навколо центра.
Отже, різних способів розміщення буде:
P10
10
=
10 !
10
= 9!
Приклад 8. На зборах мають виступати 5 чоловік — А, Б, В, Г
і Д. Скількома способами їх можна розподілити, якщо:
а) А повинен виступати перед Б;
б) Б не повинен виступати до того, як виступить А?
Розв’язання
а) Якщо А виступає безпосередньо перед Б, то ми можемо
об’єднати їх в одну групу і тоді переставлятимемо 4 елементи. Усього розподілів P4 = 4 ! = 24 ;
б) у всіх розподілах будуть пари, у яких А йде раніше Б, і навпаки, Б йде раніше А. І таких розподілів однакова кількість.
Тому розподілів, що нас цікавлять,
P5
2
=
5!
2
= 60 способів.
Задачі для самостійного розв’язування
1.
Скількома способами можна розставити 10 людей у ше­
ренгу?
2. Скільки трицифрових чисел можна скласти із чисел:
а) 3, 5, 7;
б)  3, 5, 0?
29

17.

Елементи комбінаторики
3. Скільки перестановок можна скласти із літер слова
«­привіт»?
4. Скількома способами можуть розподілитися місця між:
а) десятьма футбольними командами;
б) десятьма футбольними командами, якщо «Динамо» і «Шахтар» зайняли перші два місця?
5. Скількома способами можна розставити 5 книг з алгебри
і 3 книги з геометрії так, щоб усі книги з одного предмету:
а) стояли поруч;
б) не стояли поруч?
6. Скількома способами можна розставити книги з математики і фізики так, щоб жодні дві книги з одного предмету не стояли
поруч, якщо:
а) з фізики — 5 книг, з математики — 5;
б) з фізики — 5 книг, з математики — 4?
7. Скільки можна зробити перестановок із n елементів a, b, c, d
так, щоб елементи:
а) a, b і c стояли поруч;
б) a, b і c не стояли поруч;
в) a і b були обов’язково скраю;
г) a і b не були скраю?
8. У купе залізничного вагона є два протилежних дивани
по 5 місць у кожному. Із 10 пасажирів четверо бажають сидіти обличчям до паровоза, троє — спиною до паровоза, а решті байдуже,
як сидіти. Скількома способами можуть розміститися пасажири?
9. Скількома способами групу з восьми осіб можна розсадити
за круглим столом?
10. На зборах мають виступати 5 осіб А, Б, В, Г та Д. Скількома способами їх можна розподілити в списку виступаючих, якщо:
а) А виступає безпосередньо перед Б, але не першим;
б) Б повинен виступити до того, як виступить А?
30

18.

Елементи комбінаторики
4. Комбінації
Стислі теоретичні відомості
Комбінації, число комбінацій
•• Комбінацією з n елементів по m елементів ( n  m ) називається
будь-яка підмножина B множини A, що складається з m
елементів, причому дві такі підмножини вважаються різними,
якщо вони відрізняються складом.
Позначення: Cnm .
Читають: число комбінацій із n елементів по m елементів.
Комбінація відрізняється від розміщення тим, що в комбінації
в обраних підмножинах порядок елементів не важ­ливий.
Кількість комбінацій із n елементів по m елементів обчислюють
за формулами
Anm
Cnm =
m!
=
n ⋅ ( n − 1) … ( n − m + 1)
m!
Cnm =
n!
m ! (n − m) !
;
.
(1)
(2)
При розв’язуванні задач зручніше використовувати формулу (1).
Основні властивості числа комбінацій
n!
= Cnn−m .
Cnm =
2.
Cnm++11 =
3.
Cnm + Cnm−1 = Cnm+1 .
4.
Cn0 = Cnn = C11 = 1 .
5.
Cn0 + Cn1 + Cn2 + Cn3 + … + Cnn = 2n .
m ! (n − m) !
=
n!
1.
(n − m) ! m !
n +1 m
( n + 1) !
( n + 1) n !
=
=
C .
( m + 1) ! ( n − m ) ! ( m + 1) m ! ( n − m ) ! m + 1 n
Приклад. Скількома способами із класу в 30 учнів можна ви­
брати трьох чергових?
Розв’язання. Із 30-елементної множини вибиратимемо трьох­
елементні підмножини, причому порядок у цьому випадку не важ3
ливий. Тоді всього способів C30
=
30 ⋅ 29 ⋅ 28
1⋅ 2 ⋅ 3
31
= 4060 .

19.

Елементи комбінаторики
Приклади розв’язування задач
Приклад 1. Із класу, в якому навчається 25 учнів, потрібно ви­
брати двох школярів для участі в змаганнях. Скількома способами
це можна зробити?
Розв’язання. Із 25-елементної множини вибираємо двох­
елементні підмножини, порядок у яких не важливий. Маємо
2
C25
=
25 ⋅ 24
1⋅ 2
= 300 .
Відповідь: 300.
Приклад 2. На площині n точок розміщені так, що жодні три
не лежать на одній прямій. Скільки прямих можна провести через
ці точки?
Розв’язання. Із n точок вибираємо пари.
Усього прямих Cn2 =
Відповідь:
n ( n − 1)
2
n ( n − 1)
2
.
.
Приклад 3. Перед чемпіонатом 12 капітанів:
а) потиснули один одному руки. Скільки рукостискань було
зроблено?
б) вирішили обмінятися вимпелами. Скільки вимпелів для
цього необхідно?
Розв’язання
а) I спосіб:
2
C12
=
2
⋅
II спосіб: A12
12 ⋅ 11
2
1
2
= 66 .
= 11 ⋅12 ⋅
1
2
= 66 .
III спосіб: кожен капітан повинен зробити 11 рукостискань,
усього капітанів 12, тобто всього рукостискань 11 ⋅12 , але
при цьому кожне рукостискання враховане два рази ( A  B ) ,
тому
11 ⋅ 12
2
= 66 .
IV спосіб: перший капітан робить 11 рукостискань, другий — 10, ..., одинадцятий — одне рукостискання. Усього
11 + 10 + … 1 = 12 ⋅ 5 + 6 = 66 ;
32

20.

Елементи комбінаторики
б) I спосіб: кожній команді необхідно підготувати 11 вимпелів. Усього команд 12. Разом 11 ⋅12 = 132 вимпели.
II спосіб: із 12-елементної множини вибираємо різні впорядковані двохелементні підмножини («ти мені, я тобі»).
2
Одержуємо A12
= 12 ⋅11 = 132 .
2
III спосіб: C12
⋅ 2 = 66 ⋅ 2 = 132 .
Відповідь: а) 66; б) 132.
Приклад 4. Рота складається з 3 офіцерів, 6 сержантів і 60 рядових. Скількома способами можна виділити з них загін, що складається з офіцера, 2 сержантів і 20 рядових?
Розв’язання. Офіцерів вибираємо C31 способами, сержантів —
2
20
C6 , рядових — C60
.
20
= 3⋅
За правилом добутку маємо C31 ⋅ C62 ⋅ C60
Відповідь: 3 ⋅
6 ⋅ 5 60 ⋅ 59 ⋅ K ⋅ 41
2
⋅
20 !
6 ⋅ 5 60 ⋅ 59 ⋅ … ⋅ 41
2
⋅
20 !
.
.
Приклад 5. Шаховий гурток відвідують 2 дівчинки і 7 хлопчиків. Для участі в змаганнях необхідно скласти команду з чоти­
рьох членів, до якої обов’язково має входити хоча б одна дівчинка.
Скількома способами це можна зробити?
Розв’язання. «Хоча б одна» означає одна або дві дівчинки. Якщо до команди увійде одна дівчинка, яку можна вибрати
C21 способами, то хлопчиків можна вибрати C73 способами. Усього
C21 ⋅ C73 способів. Якщо до команди увійдуть дві дівчинки, яких можна вибрати C22 способами, то хлопчиків можна вибрати C72 способами. Усього C22 ⋅ C72 способів.
За правилом суми маємо всього
C21C73 + C22C72 =
2 ⋅1 7 ⋅ 6 ⋅ 5
1
⋅
1⋅ 2 ⋅ 3
+
2! 7 ⋅6
2!
⋅
2
= 91 спосіб.
Відповідь: 91.
Приклад 6. У одного хлопчика є 6 книг з математики, а у іншого — 8. Скількома способами вони можуть обміняти три книги одного на три книги іншого?
Розв’язання. C63 ⋅ C83 =
6 ⋅ 5 ⋅ 4 8 ⋅7 ⋅ 6
⋅
1⋅ 2 ⋅ 3 1⋅ 2 ⋅ 3
Відповідь: 1120.
33
= 20 ⋅ 56 = 1120 .

21.

Елементи комбінаторики
Приклад 7. Три стрільці повинні влучити по 15 мішеням (кожен по 5). Скількома способами вони можуть розподілити мішені
між собою?
5
Розв’язання. Для першого стрільця існує C15
різних варіантів,
другому залишиться 10 мішеней, із яких він може зробити вибір
5
C10
способами, третьому — решта 5.
5
5
Усього способів: C15
⋅ C10
⋅ C55 = 756756 .
Відповідь: 756 756.
Приклад 8. Із 15 працівників фірми директорові необхідно
вибрати бухгалтера, його помічника, двох менеджерів і чотирьох
кур’єрів. Скількома способами він може це зробити?
Розв’язання
I спосіб:
1
1
2
4
C15
⋅ C14
⋅ C13
⋅ C11
= 15 ⋅14 ⋅
13 ⋅ 12 11 ⋅ 10 ⋅ 9 ⋅ 8
2
⋅
4!
= 5405400 .
2
2
4
⋅ C13
⋅ C11
= 5405400 .
II спосіб: A15
Відповідь: 5 405 400.
Приклад 9. Є колода з 36 карт. Скількома способами можна витягнути 6 карт так, щоб:
а) був рівно один туз;
б) не було жодного туза;
в) був хоча б один туз;
г) серед цих шести був рівно один туз і один король;
д) серед цих шести були туз і король однієї масті.
Розв’язання
а) Туз із колоди можна вибрати C41 способами. Будемо вибирати решту 5 із 32 карт, тому що тузи нам уже не потрібні. Це
5
можна зробити C32
способами. Тоді маємо:
5
C41 ⋅ C32
=
4 ⋅ 32 ⋅ 31 ⋅ 30 ⋅ 29 ⋅ 28
1⋅ 2 ⋅ 3 ⋅ 4 ⋅5
= 805504 ;
б) необхідні 6 карт вибиратимемо із колоди без тузів, тобто
6
C32
= 906192 способами;
6
в) I спосіб: від усіх можливостей вибору по 6 карт, а таких C36
,
6
віднімемо ті варіанти, у яких взагалі немає тузів, тобто C32
,
тоді залишаться випадки, де серед шести буде «хоча б один
6
6
− C32
= 1041600 ;
туз»: C36
34

22.

Елементи комбінаторики
5
II спосіб: якщо туз один, то виборів буде C41 ⋅ C32
, якщо два —
4
3
2
C42 ⋅ C32
, три — C43 ⋅ C32
, чотири — C44 ⋅ C32
. За правилом суми
1
5
2
4
3
3
4
2
маємо: C4 ⋅ C32 + C4 ⋅ C32 + C4 ⋅ C32 + C4 ⋅ C32 = 1041600 ;
г) туз можна вибрати C41 способами, короля — C41 , а решта 4
4
із колоди без тузів і королів — C28
.
4
= 4⋅4⋅
Усього способів C41 ⋅ C41 ⋅ C28
28 ⋅ 27 ⋅ 26 ⋅ 25
2⋅3⋅4
= 327600 ;
4
д) C41 ⋅ C28
= 81900 .
Відповідь: а) 805 504; б) 906 192; в) 1 041 600; г) 327 600; д) 81 900.
Приклад 10. У лотереї «5 із 36» головний виграш одержить той,
хто вгадає всі 5 номерів. Той, хто вгадає 4, 3 або 2, одержує менший
виграш. Скільки може бути різних карток, де вгадано:
а) 4 номери;
б)  3 номери?
Розв’язання
а) Варіантів угадування «правильних» 4-х номерів існує C54 .
До цих 4 приєднаємо ще один «неправильний», який можна
1
4
вибрати C31
способами. Усього C54 ⋅ C31
= 155 карток;
б)
2
C53 ⋅ C31
=
5 ⋅ 4 31 ⋅ 32
2
⋅
2
= 4650 .
Зауваження. C54 = C51 , C53 = C52 .
Відповідь: а) 155; б) 4650.
Приклад 11. Скільки різних дільників має число 2310?
Розв’язання. Розкладемо число 2310 на прості множники
і складатимемо їх різні добутки (від 1 до 5 множників), тобто складатимемо різні підмножини. 2310 = 2 ⋅ 3 ⋅ 5 ⋅7 ⋅11 — усього п’ять
множників. Тоді маємо: C50 + C51 + C52 + C53 + C54 + C55 = 32 .
Зверніть увагу, що всі множники числа 2310 різні.
Відповідь: 32.
Приклад 12. Людина має 6 друзів. Щодня вона запрошує до себе
трьох із них так, що компанія жодного разу не повторюється. Скільки для цього їй потрібно днів?
Розв’язання.
Відповідь: 20.
C63 =
6 ⋅5 ⋅ 4
2⋅3
= 20 (днів).
35

23.

Елементи комбінаторики
Задачі для самостійного розв’язування
1. Скількома способами можна вибрати трьох чергових із класу, в якому навчається 20 учнів?
2. Скільки можна побудувати трикутників, якщо за їхню вершину брати вершини правильного 12-кутника?
3. Скількома способами можна вибрати з 15 різних слів набір,
що складається не більше ніж із 5 слів (зміст не важливий)?
4. У мами 2 яблука і 3 груші. Щодня протягом п’яти днів по­
спіль вона видає по одному фрукту. Скількома способами це може
бути зроблено?
5. Як зміниться розв’язання попередньої задачі, якщо до існуючих фруктів додати 4 банани?
6. П’ятеро друзів при святкуванні Нового року завжди обмінюються поцілунками і подарунками.
а) Скільки поцілунків ви зможете нарахувати?
б) Скільки подарунків необхідно для святкування Нового
року?
7. У класі навчаються 14 хлопчиків і 10 дівчаток. Для привітання гостей необхідно вибрати чотирьох хлопчиків і трьох дівчаток. Скількома способами це можна зробити?
8. Скількома способами можна:
а) розбити 15 осіб на три команди по 5 осіб у кожній;
б) вибрати з 15 осіб дві команди по 5 осіб?
9. Як зміниться розв’язання задачі 7, якщо необхідно вибрати
трьох учнів для привітання, серед яких буде:
а) хоча б одна дівчинка;
б) представники обох статей?
10. В одного учня є 7 книг з історії культури, а в іншого — 5 книг
з філософії. Скількома способами вони можуть обміняти дві книги
одного на дві книги іншого?
11. Є колода із 36 карт. Скількома способами можна витягнути
8 карт так, щоб:
а) було рівно два тузи;
б) було хоча б два тузи;
в) не було жодного туза, жодного короля;
г) були туз і король різних мастей?
36

24.

Елементи комбінаторики
12. У лотереї «6 із 49» головний приз дістанеться тому, хто вгадав усі шість номерів. Менший виграш одержать ті, хто вгадав 5, 4
або 3 номера.
Скільки може бути різних карток, де вгадані:
а) усі 6 номерів;
б) 4 номери;
в) хоча б 4 номери?
13. Людина має 10 друзів і протягом декількох днів запрошує:
а) трьох із них;
б) деяких із них так, що компанія жодного разу не повто­рю­
ється.
Скільки днів вона може так робити?
14. Скільки різних дільників має число 510?
15. Для премій з математичної олімпіади виділено три примірники однієї книги, два примірники другої і один примірник третьої.
Скількома способами можуть бути вручені премії, якщо в олімпіаді
брало участь 20 чоловік і нікому не дають два примірники однієї
книги, але можуть бути вручені дві або три різні книги?
37

25.

Елементи комбінаторики
5. Розміщення з повтореннями
Стислі теоретичні відомості
•• Розміщенням із повтореннями з n різних елементів по m елементів називається кожна його впорядкована підмножина, що
складається з m елементів, у якій елементи можуть повторю­
ватися.
Позначення:
Anm = nm .
Приклад. У школу прийшли три нові дев’ятикласники.
Скількома способами їх можуть зарахувати до школи, якщо у паралелі 9-х класів 4 класи?
Розв’язання. Кожен із учнів може потрапити або в перший, або
в другий, або в третій, або в четвертий клас. Тобто для кожного учня
існує 4 можливості. Разом за правилом добутку маємо 4 ⋅ 4 ⋅ 4 = 43 .
Очевидно, що в задачах на розміщення з повтореннями m може
бути більше n.
Класична задача. У кожний із n ящиків може бути поміщений
будь-який із m об’єктів. Скільки є варіантів такого розподілу?
Розв’язання. Перший об’єкт може бути поміщений у кожний
із n ящиків, тобто існує n способів розподілу. Для другого об’єкта
також існує n ящиків — n способів, і так для всіх об’єктів. Усього
за правилом добутку маємо: n
⋅ n ⋅ … ⋅ n = nm способів.

m
Приклади розв’язування задач
Приклад 1. На першому поверсі в ліфт сіло 10 осіб. Ліфт піднімається до 6 поверху, і на кожному поверсі можуть виходити люди.
Скількома способами можуть бути розподілені пасажири на 6 поверхах?
Розв’язання. Перший пасажир може вийти на 2, 3, ..., 6-му
поверхах. Усього 5 способів. Так само для другого, третього і решти пасажирів є по 5 способів розподілу. Тоді маємо всього 510 спо­
собів.
У даній задачі поверхи — це «ящики» (див. класичну задачу),
а пасажири — «об’єкти», що розкладаються по «ящиках».
Відповідь: 510 .
38

26.

Елементи комбінаторики
Приклад 2. Ліфт, у якому 9 пасажирів, може зупинитися
на 10 поверхах. Пасажири виходять групами по дві, три і чотири
особи. Скількома способами вони можуть вийти, якщо ліфт не повертається на поверх, на якому вже був?
Розв’язання. Умова цієї задачі відрізняється від попередньої
обмеженням на групи, а саме 2, 3 і 4 особи. Складатимемо ці групи. Вийде C92 ⋅ C73 ⋅ C44 способів складання груп. Також має значення,
на якому поверсі вийде та чи інша група, тобто важливий порядок
3
слідування груп. Розподілити їх по поверхах можна A10
спо­собами.
3
Усього маємо A10
⋅ C92 ⋅ C73 ⋅ C44 = 907200 способів.
Відповідь: 907 200.
Приклад 3. Скільки різних п’ятисимвольних букв можна
­скласти:
а) із крапок і тире;
б)  крапок, тире і двокрапок?
Розв’язання
а) Маємо розміщення з повтореннями із двох по п’ять:
A25 = 25 = 32 букви;
б) A35 = 35 = 243 букви.
Відповідь: а) 32; б) 243.
Приклад 4. Скільки різних п’ятицифрових автомобільних номерів можна скласти, якщо використовувати:
а) 10 цифр;
б) 10 цифр, але номер не може починатися з нуля;
в) 10 цифр, але до цифр праворуч додаються 3 букви російського алфавіту (без букв ь, ъ, ы, й — 29 букв);
г) не менше 10 цифр.
Розв’язання
а) На кожному з 5 місць може опинитися кожна з 10 цифр.
Усього 105 = 100 000 номерів;
б) на першому місці може опинитися кожна з 9 цифр, а на інших — кожна із 10. Усього 9 ⋅104 = 90 000 ;
в) 105 ⋅ 293 номерів;
г) одноцифрових номерів — 101 , двоцифрових — 102 і т. д.
Усього 101 + 102 + 103 + 104 + 105 =
мерів.
(
10 105 − 1
9
Відповідь: а) 100 000; б) 90 000; в) 105 ⋅ 293 ; г)
39
) = 10
(10
5
9
10
9
(10
5
)
)
−1
−1 .
но-

27.

Елементи комбінаторики
Приклад 5. Є 5 ручок і 3 олівці. Скільки є комбінацій для вибору
кількох предметів так, щоб серед обраних були і ручки, і олівці?
Розв’язання
I спосіб: кожен олівець або входить, або не входить до потрібної комбінації. Тому маємо 23 способів вибору олівців. Оскільки
хоча б один олівець має бути обраний, то виключимо той випадок,
коли жоден олівець не обраний, одержуємо 8 − 1 = 7 .
Аналогічні міркування проводимо для вибору ручок: 31 комбінація.
За правилом добутку маємо 7 ⋅ 31 = 217 .
II спосіб: складемо різні двох-, трьохелементні множини,
пам’ятаючи при цьому, що до кожної множини входить хоча б
одна ручка або один олівець. Маємо двохелементних множин C51C31 ,
трьох­елементних — C52 ⋅ C31 + C51 ⋅ C32 , ..., восьмиелементних — C55 ⋅ C31 .
(
)(
)
Усього C51 + C52 + C53 + C54 + C55 C31 + C32 + C33 = 31 ⋅7 = 217 комбі­націй.
Відповідь: 217.
Приклад 6. Палітурник повинен переплести 10 різних книг
у червону, зелену і синю палітурки. Скількома способами він може
це зробити, якщо в кожен колір має бути переплетена хоча б одна
книга?
Розв’язання. Цю задачу доцільно розв’язувати «навпаки»,
тобто 10 книг можна переплести у 3 кольори 310 способами. Якщо
для переплетення книг використовувати 2 кольори, то це буде 3 ⋅ 210
способів (червоний і зелений — 210 , червоний і синій — 210 , зелений і синій — 210 ).
Якщо ж переплітати книги якимось одним кольором, то таких
варіантів буде 3. Тепер віднімемо від загального числа способів переплетення у 3 кольори ті варіанти, коли використовується не більше двох кольорів і один колір: 310 − 3 ⋅ 210 − 3 .
Відповідь: 310 − 3 ⋅ 210 − 3 .
Приклад 7. Групі з 10 туристів (4 дітей і 6 дорослих) запропонували відвідати 5 музеїв, причому до двох із них дітей не пускають.
Скільки існує способів розподілу туристів по музеях?
Розв’язання. Діти можуть відвідати тільки 3 музеї із запропонованих, для них існує 34 способів, а дорослі — всі 5, для них —
56 способів. Усього маємо 34 ⋅ 56 способів.
Відповідь: 34 ⋅ 56 .
40

28.

Елементи комбінаторики
Задачі для самостійного розв’язування
1. Двох братів привели у Будинок дитячої творчості, де працює 5 різних гуртків. Скільки є варіантів для зарахування хлопців до гуртків, якщо кожен хлопчик може відвідувати тільки один
­гурток?
2. Номери трамвайних маршрутів колись позначали двома кольоровими ліхтарями. Яку кількість різних маршрутів можна по­
значити, якщо використовувати ліхтарі шести кольорів?
3. Два листоноші повинні рознести 8 листів за вісьмома адресами. Скількома способами вони можуть розподілити цю роботу?
4. Поїзд метро робить 10 зупинок, не враховуючи початкової,
під час яких виходять усі пасажири і не заходять нові. Скількома
способами можуть бути розподілені між цими зупинками 200 пасажирів, які ввійшли у поїзд на початковій зупинці?
5. Номер автомобільного причепа складається із двох букв і чотирьох цифр. Скільки різних номерів можна скласти, використовуючи 20 букв і 10 цифр?
6. Трамвайні маршрути позначають одним, двома або трьома
кольоровими ліхтарями. Яку кількість різних маршрутів можна
скласти, якщо використовувати ліхтарі шести кольорів?
7. Є 6 різних троянд і 3 різні гілки папороті. Скільки існує
варіантів вибору квітів за умови, що у виборі беруть участь і троянди, і папороть? (Слід врахувати, що одна троянда й одна папороть
обов’язково мають бути обрані.) Як зміниться розв’язування задачі,
якщо додасться 5 різних ромашок, які також будуть брати участь
у виборі?
8. Четверо юнаків і дві дівчини вибирають спортивну секцію.
Секцію хокею і боксу — тільки юнаки, художньої гімнастики —
тільки дівчата, а гандбол і баскетбол — і юнаки, і дівчата. Скількома способами можуть розподілитися між секціями ці шість осіб?
9. У шаховій зустрічі беруть участь дві команди по 8 членів
у кожній. Кожна пара суперників і колір фігур визначаються жеребкуванням. Яка кількість різних результатів жеребкування?
41

29.

Елементи комбінаторики
6. Перестановки з повтореннями
Стислі теоретичні відомості
Нехай є множина, що складається із n елементів, серед яких
знайдеться m однакових. Скільки різних перестановок вийде з цих
елементів?
Зрозуміло, що деякі з перестановок збігатимуться через повторювані елементи. Шукана кількість перестановок буде меншою
за число перестановок із n елементів у стільки разів, скільки перестановок можна зробити з m елементів, тобто у m! разів.
Якщо шукане число перестановок x і воно менше за число всіх
перестановок у m! разів, то x ⋅ m ! = n ! ⇒ x =
n!
m!
. Якщо в даній мно-
жині знайдеться інша група однакових елементів кількістю k, то,
міркуючи аналогічно, одержимо x =
n!
m!k!
.
Якщо в деякій множині з n елементів знайдеться k груп однакових елементів (n1 , n2 , …, nk ) , де n1 + n2 + … + nk = n , то кількість перестановок дорівнюватиме
n!
n1 ! n2 ! … nk !
і позначатиметься
Pn1 … nk , n .
Приклад. Скількома способами можна переставити букви слова:
а) «телефон»,
б)  «коробок»?
Розв’язання
а) У слові «телефон» 2 однакові букви («е»). Тоді кількість пе-
рестановок P2, 7 =
7!
2!
= 2520 ;
б) із семи букв 2 букви «к» і 3 букви «о». P2, 3, 7 =
7!
2 !⋅ 3 !
= 420 .
Приклади розв’язування задач
Приклад 1. П’ятицифровий телефонний номер складається
із двох трійок і трьох четвірок, але в якому порядку вони стоять,
хлопчик забув. Скільки йому потрібно зробити спроб, щоб напевно
додзвонитися своєму другові?
42

30.

Елементи комбінаторики
P2, 3 , 5 =
Розв’язання.
5!
2 !⋅ 3 !
= 10 (спроб).
Відповідь: 10.
Приклад 2. Скільки різних «слів» можна одержати перестановкою букв у слові:
а) «конец»;
б)  «колесо»;
в)  «перекрёсток»?
6!
11 !
Відповідь: а) P5 = 5 ! ; б) P2,6 =
; в) P2,2,2,11 =
.
2 !⋅ 2 !⋅ 2 !
2
Приклад 3. Скількома різними способами можна в 9 клітинках
розмістити букви а, а, а, б, б, б, в, в, в?
Відповідь:
9!
3 !⋅ 3 !⋅ 3 !
= 1680 .
Приклад 4. Скількома способами можна розставити 20 книг
на 5 полицях, кожна з яких може вмістити всі 20 книг?
Розв’язання. Розмістимо полиці в ряд, тоді до 20 книг до­
дасться 4 перетинки, тобто 4 однакових елементи. Кількість пере-
становок дорівнює P4 , 24 =
Відповідь:
24 !
4!
24 !
4!
.
.
Приклад 5. Клоун кидає 10 кілець на 6 стрижнів. Скільки
варіантів потрапляння кілець на стрижні може вийти, якщо клоун
жодного разу не промахнувся?
Розв’язання. До 10 кілець додається 5 проміжків між кільця-
ми. Тоді маємо P5 ,15 =
Відповідь:
15 !
5!
15 !
5!
.
.
Задачі для самостійного розв’язування
1. Знайдіть кількість різних чотирицифрових чисел, які можна одержати при перестановці цифр 2, 2, 4, 4.
2. Скільки різних «слів» можна утворити перестановкою букв
слова:
а) «змея»; б)  «змеелов»; в)  «заземление»?
3. Скільки шестицифрових чисел можна скласти із двох
«п’ятірок» і чотирьох «сімок»?
43

31.

Елементи комбінаторики
4. Скількома способами можна розставити 28 предметів
на 4 різних підставках так, щоб:
а) на кожній підставці було по 7 предметів;
б) довільним чином (кожна підставка може вмістити всі
28 предметів)?
5. Скількома способами можна надіти 5 різних кілець на пальці однієї руки, крім великого пальця?
6. Скількома способами можна розставити білі фігури (2 коня,
2 слона, 2 тури, ферзя і короля) на першій лінії шахівниці?
44

32.

Елементи комбінаторики
7. Комбінації з повтореннями
Стислі теоретичні відомості
Комбінація з повтореннями з m елементів по n елементів може
містити будь-який елемент скільки завгодно разів від 1 до p включно або не містити його зовсім.
Інакше кажучи, кожна комбінація з повтореннями з m елементів по n елементів може складатися не тільки з n різних елементів,
але з n яких завгодно і як завгодно повторюваних елементів.
Позначення: Cmn = Cnn+m−1 .
Приклад. Нехай є 5 різних видів марок і потрібно скласти з цих
елементів комбінації по 3 елементи з повтореннями (тобто до ком­
плекту можуть входити три однакові марки).
Розв’язання. Маємо сполучення з 5 елементів по 3 з повторен-
нями: C53 = C53+3−1 = C73 =
Cmn = Cmn +n−1 =
7 ⋅6 ⋅5
1⋅ 2 ⋅ 3
= 35 .
( m + n − 1) ! = P
m + n −1, n, m −1 ,
n ! ( m − 1) !
тобто задачі на комбінації
з повтореннями іноді можна звести до задач на перестановки з по­
втореннями, що було докладно розглянуто раніше (див. приклади 4
і 5 із попереднього підрозділу).
Приклади розв’язування задач
Приклад 1. Знайти кількість комбінацій із повтореннями з чотирьох елементів a, b, c, d — по 3 елементи.
Розв’язання.
C43 = C43+3−1 = C63 =
6 ⋅5 ⋅ 4
1⋅ 2 ⋅ 3
= 20 .
Відповідь: 20.
Приклад 2. У відділенні зв’язку продаються листівки 10 видів.
Скількома способами можна купити в ньому 12 листівок?
Розв’язання. Оскільки листівки можуть бути однаковими, то
12
12
12
маємо сполучення з повтореннями C10
= C10
+12−1 = C21 .
12
Відповідь: C21
.
45

33.

Елементи комбінаторики
Приклад 3. Скільки існує трикутників, довжини сторін яких набувають одного зі значень: 4, 5, 6, 7, 8?
Розв’язання.
C53 = C73 =
7 ⋅6 ⋅5
1⋅ 2 ⋅ 3
= 35 .
Відповідь: 35.
Приклад 4. Скільки можна побудувати різних прямокутних
паралелепіпедів, довжина кожного ребра яких є цілим числом
від 1 до 10?
Розв’язання.
3
3
C10
= C12
=
12 ⋅ 11 ⋅ 10
1⋅ 2 ⋅ 3
= 220 .
Відповідь: 220.
Задачі для самостійного розв’язування
1. Знайдіть кількість комбінацій із повтореннями з шести елементів: а, б, в, г, д, е — по 4 елементи.
2. У кондитерському магазині є тістечка чотирьох видів: заварні, пісочні, «наполеон» і «корзинка». Скількома способами можна
купити в ньому 10 тістечок?
3. Скільки існує п’ятикутників, довжини сторін яких набувають значення з набору чисел 4, 5, 6, 7?
46

34.

Елементи комбінаторики
8. Підсумкова таблиця
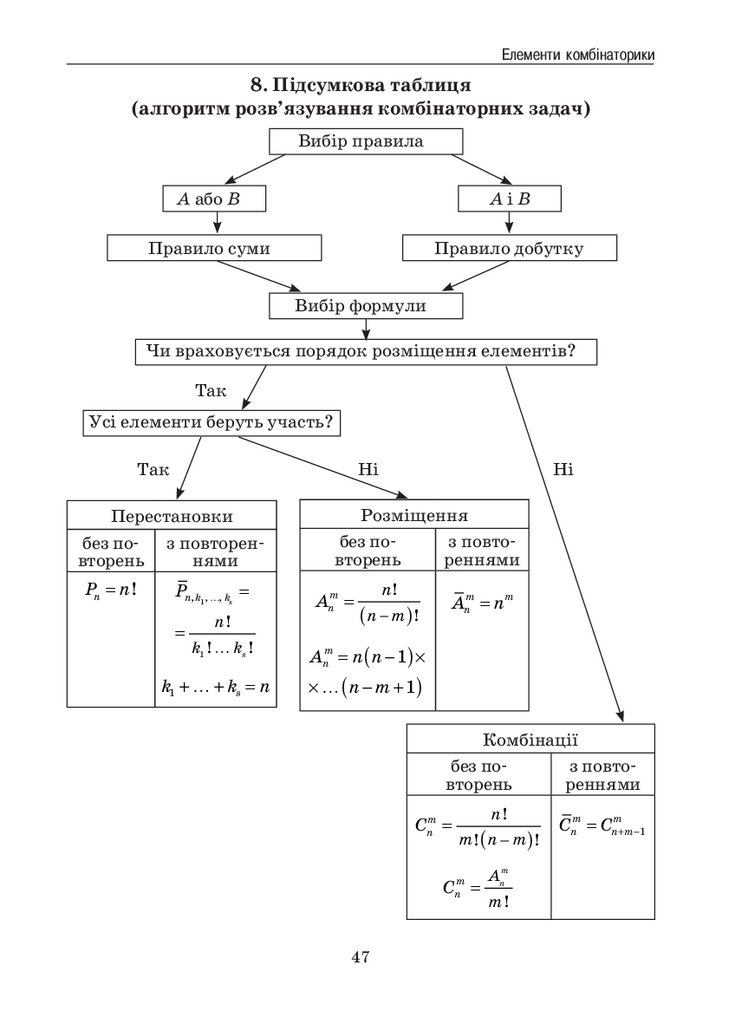
(алгоритм розв’язування комбінаторних задач)
Вибір правила
A або B
AіB
Правило суми
Правило добутку
Вибір формули
Чи враховується порядок розміщення елементів?
Так
Усі елементи беруть участь?
Так
Ні
Перестановки
без по­
з повторенвторень
нями
Pn = n !
Pn, k1 , …, ks =
=
n!
k1 ! … ks !
k1 + … + ks = n
Ні
Розміщення
без по-­
з повтовторень
реннями
Anm =
n!
(n − m) !
Anm = nm
Anm = n (n − 1) ×
× … (n − m + 1)
Комбінації
без по-­
з повтовторень
реннями
Cnm =
Cnm =
47
n!
m ! (n − m) !
Anm
m!
Cnm = Cnm+m−1

35.

Елементи комбінаторики
Самостійна робота
I варіант (з розв’язаннями)
У завданнях 1—2 виберіть одну правильну, на вашу думку, відповідь.
1. Вставте пропущене слово: розміщення з m елементів по n елементів — це будь-яка ... підмножина m-елементної множини, що
містить n елементів.
А
Б
упорядкована
невпорядкована
Розв’язання. У розміщенні важливий порядок.
Відповідь: А.
2. Кожна з перестановок, утворена з 5-елементної множини,
містить елементів:
А
Б
В
Г
Д
125
25
5
10
120
Розв’язання. У перестановках беруть участь усі елементи.
Відповідь: В.
3. Обчисліть кількість комбінацій із 7-елементної множини
по 3 елементи в кожній.
Розв’язання.
C73 =
7 ⋅6 ⋅5
1⋅ 2 ⋅ 3
= 35 .
Відповідь: 35.
4. Скількома способами можна розмістити 6 ліхтарів у новорічній гірлянді?
Розв’язання. Розміщення ліхтарів у гірлянді — це перестановки 6 елементів. P6 = 6 ! = 720 .
Відповідь: 720.
5. Скільки різних трицифрових чисел можна скласти з цифр
1, 2, 3, 4, 5?
Розв’язання. Вибираємо різні впорядковані 3-елементні підмножини із 5-елементної множини. A53 = 5 ⋅ 4 ⋅ 3 = 60 .
Відповідь: 60.
6. Скількома способами можна скласти команду із 2 дівчаток
і 3 хлопчиків для участі в олімпіаді, якщо є 10 дівчаток і 12 хлоп­
чиків?
48

36.

Елементи комбінаторики
2
Розв’язання. Двох дівчаток із 10 можна вибрати C10
способа3
ми. Трьох хлопчиків із 12 — C12 способами. За правилом добутку
2
3
⋅ C12
=
маємо C10
10 ⋅ 9 12 ⋅ 11 ⋅ 10
1⋅ 2
⋅
1⋅ 2 ⋅ 3
= 5 ⋅ 9 ⋅ 6 ⋅ 11 ⋅10 = 9900 .
Відповідь: 9900.
II варіант
У завданнях 1—2 виберіть одну правильну, на вашу думку, відповідь.
1. Вставте пропущене слово: кожна перестановка, утворена
з елементів деякої множини,— це ... множина.
А
Б
упорядкована
невпорядкована
2. Із елементів 5-елементної множини можна утворити різних
неупорядкованих підмножин:
А
10
Б
25
В
16
Г
32
Д
120
Чому дорівнює кількість перестановок із 4 елементів?
4. Скількома способами можна вибрати двох учасників естафети 100 × 200 із 6 спортсменів?
5. На площині 20 точок розмістили так, що жодні 3 не лежать
на одній прямій. Скільки різних прямих можна провести через ці
точки?
6. Скількома способами можна розставити на полиці 5 синіх
і 3 зелені книги так, щоб зелені завжди стояли поруч?
3.
III варіант
У завданнях 1—2 виберіть одну правильну, на вашу думку, відповідь.
1. Вставте пропущене слово: комбінацією з m елементів
по n елементів називають будь-яку ... підмножину, що містить
n елементів.
А
Б
упорядковану
невпорядковану
49

37.

Елементи комбінаторики
2.
Перестановка із n елементів — це:
А
Б
В
Г
Д
розміщення розміщення комбінація комбінація
по n елемен- по n елемен- по n елемен- по n елементів із m еле- тів із n еле- тів із m еле- тів із n елементів
ментів
ментів
ментів
ані розміщення,
ані комбі­
нація
3. Обчисліть кількість розміщень із 7-елементної множини
по 3 елементи в кожному.
4. Скількома способами можна вибрати два ліхтарі для новорічної гірлянди з наявних шести?
5. Скільки елементів містить множина, якщо кількість усіх
можливих перестановок із її елементів не перевищує 120?
6. Скільки різних чотирицифрових чисел можна скласти
із цифр 0, 2, 5, 6, 9, не повторюючи їх?
Контрольна робота 1
I варіант
У завданнях 1—5 виберіть одну правильну, на вашу думку, відповідь.
1. Кількість розміщень із n елементів по m елементів обчислюється за формулою:
А
Б
В
Г
Д
Pn = n !
Pm = m !
Anm =
n!
(n − m) !
Cnm =
n!
m ! (n − m) !
n ⋅m
2. Якщо при виборі елементів не враховується порядок і не всі
елементи беруть участь у виборі один раз, то це:
А
Б
В
Г
Д
розміщення перестановкомбінарозміщення перестановка з повторен- ки з повтоція
нями
реннями
3. Скількома способами із букета, що складається з 5 троянд
і 7 гвоздик, можна вибрати або троянду, або гвоздику?
А
Б
В
Г
Д
5 ⋅7
2⋅5
7−5
5 +7
2 +7
50

38.

Елементи комбінаторики
4.
Обчисліть C72 .
А
Б
7 ⋅ 2 = 14
5.
В
Г
7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 = 2520
7 ⋅ 6 = 42
7+2=9
7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 = 2520
Виберіть правильну рівність.
А
Б
В
A =A
2
5
3
5
Д
C =C
1
6
C =C
6
6
1
6
5
6
7⋅6
= 21
1⋅ 2
Г
Д
A =A
1
5
5
5
C = C65
0
6
6. Скількома способами можна розподілити призові місця серед 10 команд, що змагаються?
7. Скількома способами можна вибрати 4 олівці й 2 ручки
з 6 різних олівців і 5 різних ручок?
8. Скільки різних трицифрових чисел можна скласти з цифр
0, 1, 2, 3, 4 так, щоб жодна цифра не повторювалася?
9. Скільки різних «слів» можна скласти з букв слова «ймо­
вірність»?
10. Підкидають два гральні кубики. Скільки є можливих варіантів випадання різних цифр на кубиках?
11. Між шістьма гравцями в карти порівну розподіляються
36 карт. Скількома способами можуть розподілитися карти?
12. Скільки існує різних шестицифрових номерів, якщо номер
не може починатися з нуля?
II варіант
У завданнях 1–5 виберіть одну правильну, на вашу думку, відповідь.
1. Число комбінацій із n елементів по m елементів обчислюється за формулою:
А
Б
В
Г
Д
Pn = n !
Pm = m !
Anm =
n!
(n − m) !
Cnm =
n!
m ! (n − m) !
n ⋅m
2. Якщо при виборі елементів ураховується порядок, але беруть участь не всі елементи і без повторень, то це:
А
Б
В
Г
Д
комбіна- розміщенпереста­
розміщення
комбінація
ція
ня
новка
з повторенням з повторенням
51

39.

Елементи комбінаторики
3. Скількома способами із букета, що складається з 5 троянд
і 7 гвоздик, можна вибрати одну троянду й одну гвоздику?
А
Б
В
Г
Д
5 ⋅7
4.
7−5
5 +7
2 +7
В
Г
Д
2
7
Обчисліть A .
А
7 ⋅ 2 = 14
5.
2 ⋅7
Б
7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 = 2520
7 ⋅ 6 = 42
7+2=9
7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 = 2520
Виберіть правильну рівність.
А
Б
В
Cnm = Pn , m
Cnm =
m
n
A
m!
Cnm = Anm
7⋅6
1⋅ 2
= 21
Г
Д
Pn = Anm
Pn, m = Anm
6. Скількома способами можна відправити на екскурсію чотирьох осіб із групи в 10 осіб?
7. Скільки різних «слів» можна скласти з букв слова «соче­
тание»?
8. Скількома способами можна розставити в шеренгу 5 дівчат
і 7 юнаків, щоб усі дівчата стояли скраю?
9. Скільки різних чотирицифрових чисел можна скласти
з цифр 0, 1, 2, 3, 4 так, щоб жодна цифра не повторювалася?
10. Скількома способами з колоди в 36 карт можна витягнути
5 так, щоб серед них була одна дама?
11. Скільки різних чотирицифрових чисел можна скласти
із цифр 0, 1, 2, 3, якщо в записі кожного з цих чисел одна й та сама
цифра може повторитися кілька разів?
12. 12 студентів слід рівномірно розподілити по трьох різних
групах. Скількома способами це можна зробити?
52