Математика. Основные разделы теста. 1 семестр

1. Математика 1 семестр

2.

Основные разделы теста

3.

Основные разделы теста
Матрицы и определители
Определители 2-го порядка
Определители 3-го порядка
Разложение определителя по элементам какого-либо
столбца (строки)
Свойства определителей
Сложение матриц, умножение на число и
транспонирование
Умножение и обращение матриц

4.

Системы линейных уравнений
Основные понятия: совместность, решение, общее
решение, однородная СЛУ (ОСЛУ), неоднородная СЛУ
(НСЛУ)
Правило Крамера решения СЛУ
Критерий совместности СЛУ (теорема КронекераКапелли)
Решение СЛУ методом Гаусса, понятия базисных и
свободных переменных
Структура общего решения НСЛУ
Структура общего решения ОСЛУ, фундаментальная
система решений
Формы записи: стандартная, матричная

5.

Векторная алгебра
Линейные операции над векторами
Перпендикулярные и коллинеарные векторы
Использование базисов на плоскости и в пространстве
Скалярное произведение векторов. Длина вектора. Угол
между векторами.
Векторное произведение и его геометрическая
интерпретация
Смешанное произведение векторов и его
геометрический смысл

6.

Аналитическая геометрия
Декартова система координат: координаты точек и
векторов, вычисление длины и середины отрезка в
координатах
Полярная система координат: координаты точек,
уравнения линий
Уравнения прямой в пространстве: общее, каноническое,
параметрическое
Общее уравнение плоскости
Взаимное расположение прямой и плоскости в
пространстве
Кривые второго порядка
Поверхности второго порядка

7.

Предел ФОП
Определение, формула общего члена числовой
последовательности
Понятие функции, ее области определения, множества
значений и графика функции
Понятие предела функции в точке, связь предела
функции и односторонних пределов, свойства пределов,
связанные с арифметическими операциями
Бесконечно малые и бесконечно большие функции
Замечательные пределы
Предел рациональной функции
Пределы функций, содержащих иррациональности
Понятие непрерывной функции в точке; точки разрыва

8.

Дифференциальное исчисление ФОП
Определения производной и дифференцируемости
функции в точке; правила дифференцирования; таблица
производных
Геометрический смысл производной
Дифференцирование степенно-показательной функции
Исследование функции на локальный экстремум
Исследование функции на наибольшее (наименьшее)
значение на отрезке
Формула Тейлора

9.

Дифференциальное исчисление ФНП
Частные производные
Экстремум: локальный, глобальный, условный
Касательная плоскость и нормаль к поверхности
Производная по направлению
Градиент

10.

0 1 1 1
Определитель 1 0 1 1 равен
1 1 0 1
1 1 1 0
а) -3; б) 3; в) -2; г) 5; д) 0.

11.

1 2 3
Произведение матриц
3 2 5
2 1 1
а)
не определено
б)
равно
в)
2 5
4
равно
20
10
25
г)
2 5
3
равно
15
10
25
4 5
3
15 20 25

12.

Если произведение матриц (АВ)С определено, то
а) произведение А(ВС) также определено и всегда (АВ)С=А(ВС)
б) произведение А(ВС) также определено, но не всегда (АВ)С=А(ВС)
в) А, В, С всегда являются квадратными матрицами одного и того же
порядка
г) произведение А(ВС) может быть и не определено

13.

Обратная к произведению обратимых матриц AB равна
a) A 1B 1
b) AT BT
c) B 1 A 1
d ) BT AT

14.

Если ранг расширенной матрицы системы уравнений НЕ равен рангу ее
основной матрицы, то
а) эта система несовместная
б) эта система неоднородная
в) ранг расширенной матрицы системы больше ранга основной матрицы
системы на 2
г) ранг расширенной матрицы системы больше ранга основной матрицы
системы на 1

15.

Векторная форма общего решения неоднородной системы линейных уравнений
7x1 11x2 6x3 3x4 15,
3x1 5x2 2x3 x4 7,
4x 6x 4x 2x 8
2
3
4
1
а) 1, 2,1, 2 8, 4, 2,0 0,0,1, 2 ,
, R
б) 1,1,1,1 4, 2,1,0 2,1,0,1 ,
, R
в) 3, 2,1, 2 2, 1,1,0 2,1,0,1 ,
, R
г)
1,1,1,1 4, 2,1,0 2,1,0,1 , , R

16.

x1 2x2 x3 1,
x x2 2,
Решение системы 1
2x x 1
1 3
б)
52 , 0, 0
54 , 56 , 53
в)
0, 0, 0
г)
54 , 56 , 0
а)
М.б. вопрос про сумму решений системы

17.

x1 x2 x3 3,
Система линейных уравнений 2 x1 3x2 x3 1, совместна при
3 x 4 x 2 x
2
3
1
3
2
3
2
2

18.

Координаты векторного произведения a, b векторов
a a1, a2, a3 , b b1, b2, b3 в правом ортонормированном базисе i, j, k
вычисляются по формуле
i
j
k
а) a, b a1 a2 a3
b1 b2 b3
i
j k
б) a, b a1 a2 a3
b1 b2 b3
i
j
k
в) a, b a1 a2 a3
b1 b2 b3
i
j k
г) a, b a1 a2 a3
b1 b2 b3

19.

Смешанное произведение некомпланарных векторов a, b, c отрицательно
тогда и только тогда, когда векторы a, b, c
а) образуют левую тройку
б) компланарны
в) образуют ортонормированный базис
г) образуют правую тройку

20.

Векторы a 1, 2, 3 , b 1, 2, 4 , c 0, 0, 3
а) некомпланарны
б) образуют ортогональный базис
в) компланарны
г) образуют ортонормированный базис

21.

Смешанное произведение 2a b 2b c a 2c равно
2abc
abc
2abc
9abc

22.

Площадь треугольника с вершинами A 1;2;3 , B 1; 2;4 , C 0;0;3 равна
2
21
21
2
21
4

23.

x2 y2
Расстояние между фокусами эллипса
1 равно
14 5

24.

Малая полуось эллипса, изображенного на рисунке, b=1. Расстояние между
его фокусами равно
O
3
-1
а)
3 ; б) 2 5 ; в)
x
5 ; г) 2 3 .

25.

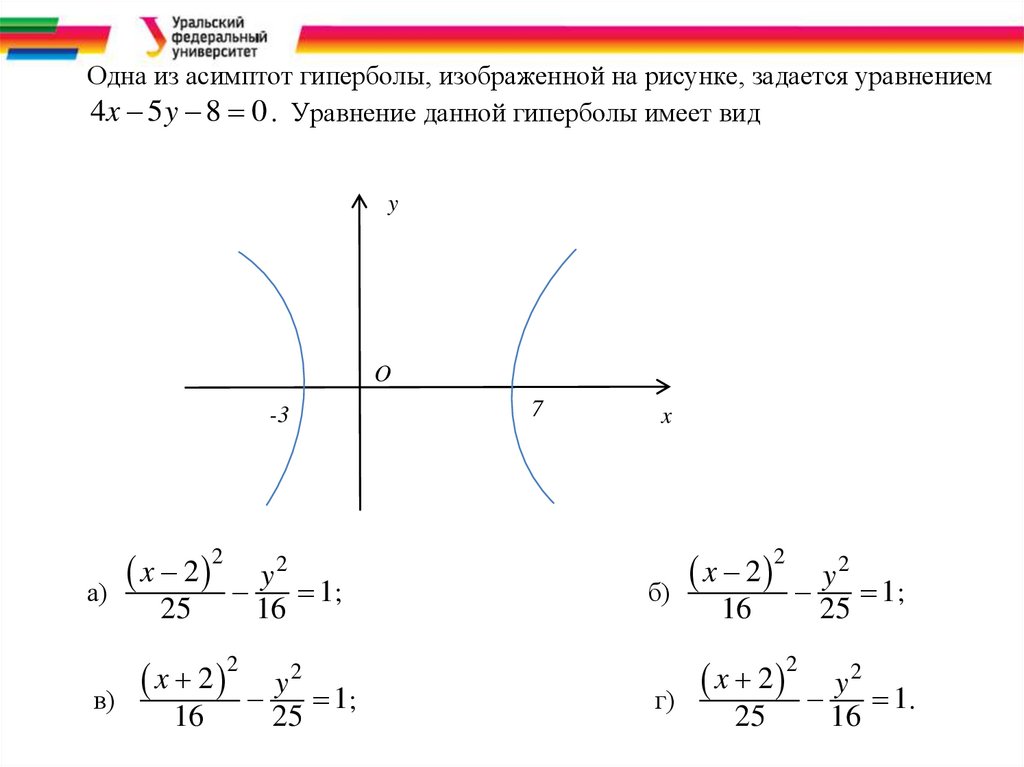
Одна из асимптот гиперболы, изображенной на рисунке, задается уравнением
4x 5 y 8 0 . Уравнение данной гиперболы имеет вид
y
O
-3
7
x
2
x 2
y2
1;
а)
2
x 2
y2
1;
б)
x 2
y2
1;
в)
16
25
x 2
y2
1.
г)
25
16
25
16
2
16
25
2

26.

Расстояние от точки a, b, c до плоскости Ax By Cz D 0 равно
а) Aa Bb Cc D
A2 B 2 C 2
б) Aa Bb Cc
в)
г)
д)
Aa Bb Cc D
A2 B 2 C 2
Aa Bb Cc
A2 B 2 C 2
Aa Bb C
A2 B 2 C 2

27.

Пусть угол между плоскостями x z 4 0 и 4x y 8z 5 0 .
Тогда число 99 2 cos равно…

28.

Пусть угол между прямой
плоскостью x y 10 0.
x 1 y 3 z 4 и
2
1
2
Тогда число 9 2 sin равно…

29.

Плоскость задана уравнением x A y B z C 0 .
Тогда , ,
точка, лежащая на плоскости, A, B,C вектор перпендикулярный
плоскости
вектор перпендикулярный плоскости, A, B,C точка, лежащая на
плоскости
вектор параллельный плоскости, A, B,C вектор перпендикулярный
плоскости
вектор параллельный плоскости, A, B,C точка, лежащая на плоскости

30.

x at ,
Прямая y b 2t , лежит в плоскости x 2 y 5z 1 0. Тогда произведение ab
z 1 3t
равно

31.

В сечении эллиптического цилиндра
x2
a
2
y2
b
2
1 плоскостью, параллельной
Oxz
гипербола или две пересекающиеся прямые
эллипс
две параллельные, две совпадающие прямые или пустое множество
парабола

32.

2
x2 y z
a 2 b2
2
x 2 y z 2 1
a 2 b2 c 2
2
x2 y z 2 1
a 2 b2 c 2
Вопрос на соответствие

33.

Последовательность xn n3 n 1 n
Бесконечно малая
Бесконечно большая
Неограниченная
Ограниченная

34.

Область определения функции f x 3tg (4 x) есть
x
n
, n Z
4
8
x n, n Z
n
, n Z
x
4
x
2
n, n Z
x 2 n, n Z
x R

35.

Предел функции
lim
x
43
3 x 8
4
1
3x 3 x 2 2
равен …

36.

Предел функции
2
sin
2x равен
lim
x 0
x2
а) 0; б) 2; в) 8; г) 1; д) 4

37.

Вычислить lim 3 x 1 3 x 1
x

38.

Предел функции lim 1 3tgx ctgx равен
x 0
1
e3
e 3
e
1
0

39.

Предел функции lim
x 1
равен
3 x 1 x3 1
x3 1

40.

Предел функции lim
x 1
равен
18 3 x 1
x2 1

41.

1
Функция имеет разрыв f x 1 2 x 3 x , x 0, f 0 0 в точке x0 0 имеет
разрыв
Второго рода
Первого рода
Устранимый

42.

5 x x
Функция f x
, x 0; f 0 0 в точке x0 0
2x
а) непрерывна
б) имеет разрыв первого рода
в) имеет разрыв второго рода
г) имеет устранимый разрыв

43.

Производная функции f x ln(2 x 1) равна
x
2x
ln(2 x 1)
a) 2 x 1 2
x
x
ln(2 x 1)
b) 2 x 1 2
x
2x
ln(2 x 1)
1
x
2
c)
x2
ln(2 x 1)
d)
x2
2x
2x 1

44.

Производная функции f x 6x e
arcsin x
в точке x0 0
равна …

45.

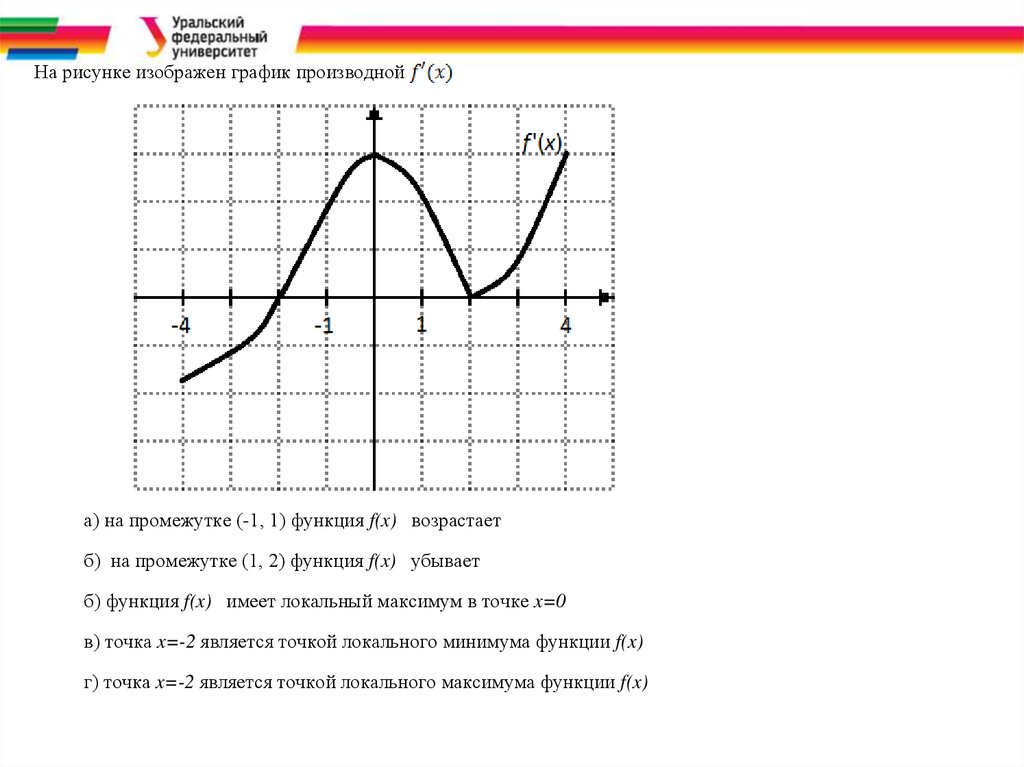
Производная первого порядка f x ln( x 2 2 x) в точке x 1 равна…

46.

На рисунке изображен график производной
а) на промежутке (-1, 1) функция f(x) возрастает
б) на промежутке (1, 2) функция f(x) убывает
б) функция f(x) имеет локальный максимум в точке x=0
в) точка x=-2 является точкой локального минимума функции f(x)
г) точка x=-2 является точкой локального максимума функции f(x)

47.

Разложение функции f x x 2 sin x по формуле Тейлора 7-го порядка с
остаточным членом в форме Пеано в точке x0 0
имеет вид
x5 x 7
f x x
2! 5!
3
2
x3 x5
f x x x o x5
3! 5!
x3 x7
f x x
o x9
3! 5!
3
x5 x 7
f x x
o x7
3! 5!
3

48.

Наибольшее значение функции f x x 2x 10 на отрезке [0, 5]
4
равно…
2

49.

Наибольшее значение функции f x 5x 2 15 x 2 на отрезке 3;1 равно

50.

Касательная к графику функции f x x 3 5 в точке x0 4 задается
уравнением
y 5x 4
y 4 5( x 1)
y 1 5( x 4)
y 5x 1

51.

Если z sin v u 3, u u x, y , v v x, y , то z равно
x
cos v 3u 2 u
x
cos v 3u 2
cos v v 3u 2 u
x
x
sin v v u3 u
x
x

52.

Если z e3u v, u u x, y , v v x, y , то z равно
x
3e3u v x
3e3uu x v x
3e3uu x vv x
3e3uu xv y

53.

Для функции z x y e
2
а) 4 e
2
б) 4 2e
2
б) 4 2e
в) 4 2e
г) 4 2e
2
2
2
xy
частная производная z в точке M(-1,2) равна
x

54.

Функция z x 2 xy y 2 3x 6 y в точке x 0, y 3
а) имеет максимум
б) имеет минимум
в) не имеет экстремума