Похожие презентации:
Матрицы, операции над матрицами, теорема существования обратной матрицы. Матричная запись систем линейных уравнений
1. Лекция 3. Матрицы, операции над матрицами, теорема существования обратной матрицы. Матричная запись систем линейных
алгебраических уравнений. Метод обратнойматрицы решения СЛАУ, формулы Крамера.
Ранг матрицы. Теорема Кронекера-Капелли,
теорема о базисном миноре, метод Гаусса
решения СЛАУ. Однородные системы линейных
алгебраических уравнений, фундаментальная
система решений ОСЛАУ.
1
2.
§1. Матрицы и действия над ними.Определение. Матрица – прямоугольная
таблица из m n действительных чисел,
расположенных в m строк и n столбцов.
Обозначение: A,B,C,D . . . . . ( ), [ ], || || .
a11 a12
a
a22
21
A
am1 am 2
a1n
a2 n
amn
2
3.
Матрица, все элементы которой нули,называется нулевой.
Матрицы у которых соответственно равны
числа строк и столбцов называются
матрицами одного размера.
Две матрицы одного размера у которых
соответствующие элементы равны,
называются равными.
3
4.
Различные виды матрицМатрица состоящая из 1 строки называется строкой.
Матрица состоящая из 1 столбца называется столбцом.
Если m ≠ n , то матрица прямоугольная.
Если m = n , то матрица квадратная.
A = (a1,a2,a3) - матрица строка
b1
В b2
b
3
- матрица столбец
Для квадратной матрицы вводят понятия главной и
побочной диагонали
a b
c d
побочная
главная
5.
Матрица у которой отличны от нуля лишь элементыглавной диагонали называется диагональной.
a
0
b
0
c
Диагональная матрица у которой элементы главной
диагонали равны называется скалярной.
a
0
a
0
a
Скалярная матрица у которой элементы главной
диагонали единицы называется единичной.
1 0 0 0
0 1 0 0
Е
0
0
0
1
6.
Операции над матрицами1.) Транспонирование – замена всех строк матрицы
столбцами с сохранением номеров (At)
1
для А – > At
1 2 3 4
2
t
А
5 6
7 8
5
6
А
3 7
4 8
Если А=At , то А –симметричная.
2.) Линейные операции над матрицами: сложение
матриц, умножение матрицы на число.
2.1. Операция сложения возможна для матриц одного
размера.
Определение: Суммой двух матриц Amxn=[aij] и Bmxn[bij]
наз.третья матрица С, того же размера Сmxn=[сij]
сij = aij + bij
т.е. при сложении матриц их соответствующие элемент
складываются
С=А+В
7.
2.2. Произведением Amxn на λ ϵ R (или λ ϵ R на А)называется Bmxn[bij], bij = λaij (A = [aij] ) B=λ·A
Матрица (-1)·А называется противоположной для А и
обозначается –A.
Сумма матриц С и –А называется их разностью и
обозначается С - А.
2.3. Свойства линейных операций (+) и (·)
1.
АиВ A B B A
2.
B, A, C A B C A B C
3.
A A 0 A
4.
A A ( A) 0
5.
A 1 A A
6.
Aи R
7.
, Rи A
8.
AииВи K R
A A A
A A A
K A B KA KB
8.
План доказательства.1.) Показать, что матрицы слева и справа имеют один и
тот же размер
2.) Показать, что соответствующие элементы этих матриц
равны.
3.) Произведение матрицы А на матрицу В определено
лишь в случае, если число столбцов матрицы А равно
числу строк матрицы В.
Определение: Произведением матрицы Amxp [aij] на
матрицу Bmxp[bij] называется матрица Сmxn [сij] , элемент
которой сij равен сумме произведений элементов i-ой
строки матрицы А на соответствующие элементы j-го
столбца матрицы В.
A2 2
1 2
0
4
B2 2
1 2
3
4
A B2 2
9.
A B2 21 2 1 2 1 ( 1) 2 3 1 2 2 4 5 10
0 4 3 4 0 ( 1) 4 3 0 2 4 4 12 16
B A2 2
1 2 1
3 4 0
2 1 6
4 3 22
AB BA
В общем случае AB ≠ BA, если AB = BA, то матрицы А и
В называются перестановочными.
Можно показать, что единичная матрица перестановочна
с любой квадратной матрицей того же размера, причем
A·E = E·A = A
10.
Свойства операции умножения.Предположим, что все указанные операции выполнимы
1.
А, В, С
А( ВС ) ( АВ)С
2.
А, В, С
( А В)С АС ВС
3.
А, В, С
А( В С ) АВ АС
4.
А( В) ( А) В ( АВ) , А, В и R
5.
А и
В
( АВ) t В t Аt
11.
§2. Обратная матрица. Матричные уравнения.Формулы Крамера.
Теорема об определителе квадратных матриц.
Теорема: Определитель произведения двух квадратных
матриц равен произведению определителей этих матриц.
0 1
;
А
2 4
3 4
В
1 5
показать
0 1 3 4 1 5
;
АВ
2 4 1 5 2 28
А
0 1
2 4
2
В
3
АВ
4
1 5
19
АВ А В
1
5
2
28
28 10 38
А В 2 19 38
12.
(2) Определение квадратной матрицы.Определение: Квадратная матрица А называется
вырожденной (особенной), если ее определитель = 0 и
невырожденной(не особенной),если ее определитель ≠ 0.
Определение: Матрица А называется обратной для
матрицы В если А×В = В×А = Е (единичной матрице)
Теорема существования обратной матрицы.
Теорема: Для того чтобы матрица А имела обратную
необходимо и достаточно, чтобы она была не
вырожденной.
13.
Необходимость. Пусть А имеет обратную В. Тогда поопределению АВ = ВА = Е, АВ = Е.
(*)
По теореме об определителе квадратной матрице
АВ А В
Е 1
(**)
Из (*) => что если матрицы =, то = их определители
АВ Е
Из (*) => А В 1 0
А 0
(невырожденная)
Достаточность. А - невырожденная, т.е. |А| ≠ 0
a11 a12 ... a1n
А ai1 ai 2 ... ain i я
an1 an 2 ... ann
j й
А11 А j 2 ... Аn1
А А12 А j 2 ... Аn 2
А1n А jn ... Аnn
14.
В1
А ;
А
АВ ВА Е
Обозначим
АВ С
С
ij
1
1 A,i j
Сij аi1 A j1 аi 2 A j 2 ... аin A jn
;
А
А 0, i j
1, i j
Сij
, т.е. С единственная
0, i j
Единственность обратной матрицы.
Теорема: Если А имеет обратную, то она (обратная)
единственная.
Доказательство: Пусть В обратная для А. Предположим,
что С тоже обратная для А и С совпадает с В, С = В.
15.
Так как В обратная для А, то АВ = ЕУмножим обе части равенства слева на матрицу С
С(АВ) = СЕ
ЕВ = С
(СА)В = С
В=С
Е
.
С=В
Обозначение А обратная А-1
Например, n = 3:
а11
А а21
а31
n 2
а13
А11
а22 а23 ;
А 1 А12
А13
а32 а33
а11 а12
1
1
А
;
А
А
а21 а22
а12
А31
1
А22 А32
А
А23 А33
А11 А21 1 а22
А12 А22 А а21
А21
а12
а11
16.
Свойства обратной матрицы.1.
А 1
1
А
2.
А
А
3.
АВ 1 В 1 А 1
4.
1 1
А
t 1
( множители
переставляются)
А 1 А t
Доказатель ство
t
АА 1 Е
1:
АА
А А 1 1
Доказатель ство
А 1
3:
1
1
Е
1
А
1
1
1
АB
В
А
С
C 1
С С 1 С 1 С Е
( АВ)( В 1 А 1 ) А( ВВ 1 ) А 1 ( АЕ ) А 1 АА 1 Е
( В 1 А 1 )( АВ) св во
произв. В 1 ( А 1 А) В ( В 1 Е ) В В 1 В Е
17.
Матричные уравнения.Матричными уравнениями называются уравнения вида:
АХ = В (1)
ХС = D (2), где
|А| ≠ 0, |С| ≠ 0 – невырожденные матрицы
Х - неизвестная матрица,
В, D - известные матрицы размеры которых не
противоречат операциям умножения.
т.к. |А| ≠ 0, то А-1 существует. Умножим обе части
уравнения (1) слева на А-1.
А-1(АХ) = А-1 В
(А-1 А)Х = А-1 В ЕХ = А-1 В Х = А-1 В (1)
18.
т.к. |С| ≠ 0, то С-1 существует. Умножим обе частиуравнения (2) слева на С-1.
С-1(ХС) = С-1 D
Х(С-1 С) = D С-1 ХЕ = D С-1 Х = D С-1 (2)
Если А и С – вырожденные матрицы, то уравнения могут
не иметь решения или иметь их бесчисленное
множество.
Матричная запись системы уравнений.
Рассмотрим систему m линейных уравнений с n
неизвестными.
a11 x1 a12 x2 ... a1n xn b1
a x a x ... a x b
21 1 22 2
2n n
2
am1 x1 am 2 x2 ... amn xn bm
(1)
19.
Введем А - матрицу системы (1), полученную изкоэффициентов при неизвестных
a11
a21
А
...
am1
a11
a21
...
am1
a12
a22
...
am 2
a12
a22
...
am 2
Аm n
... a1n
... a2 n
... ...
... amn
x1
x2
X
...
xn
... a1n x1 b1
... a2 n x2 b2
... ... ... ...
... amn xn bm
X n 1
bm 1
b1
b2
B
...
bm
AX B (1 )
матричная
запись системы(1)
20.
Пример.{ x1 2 x2 1 1
2 x1 1
A X B
x1 x2 0
1
1
x2 0
2 1 1
1
1 1 2 1 3 2 3
1
1
3 3
X A B; A
X 3
1
1
1 0 1
3 1 1 1
3
3
3
3
3
21.
Замечание: неизвестные и свободные члены можнорасположить в строки, то запись имела бы
соответствующий вид.
Теорема Крамера.
Рассмотри систему n линейных уравнений с n
неизвестными
a11 x1 a12 x2 ... a1n xn b1
a x a x ... a x b
21 1 22 2
2n n
2
... ... ... ... ...
an1 x1 an 2 x2 ... ann xn bn
(1)
22.
Составим определитель из коэффициентов принеизвестных - определитель системы.
А
a11
a12
... a1n
a21
a22
... a2 n
...
...
... ...
an1
an 2
... ann
Теорема. Если определитель квадратной системы
отличен от нуля, то система имеет единственное
решение, которое можно найти по формулам:
1
Х1 ;
2
Х2
;
...
n
Хn
;
23.
Δ - определитель системыΔk (k = 1,2…) - определитель, полученный из
определителя системы заменой k-ого столбца, столбцом
свободных членов.
(*) – формулы Крамера, а применение их к решению
системы называют Правилом Крамера.
Доказательство:
1.) доказательство существования решения
2.) доказательство единственности решения
3.) вывод формул (*)
24.
Пример.{ x1 2 x 2 1 A 1
x1 x 2 0
то есть решение
x1
2
1 2
1 1
; A 3 , 1
1; 2
1
0 1
1 0
1 1
1 1
1
; x2 .
3
3
ЗАМЕЧАНИЕ
Для решения СЛУ с матрицей А размера выше 4 метод Крамера не
стоит применять, т.к. число операций при применении этого метода имеет
порядок n!, т.е. быстро растет с порядком системы. (n!=n (n-1) (n-2)...3 2 1,
5!=5 4 3 2 1=120).
При решении СЛУ высокого порядка лучше применять метод Гаусса.
Суть метода Гаусса состоит в том, что при помощи преобразований, не
нарушающих равносильности, исходная система сводится к треугольному
виду.
25.
Ранг матрицы, его свойства и вычисление. Системы линейных уравненийРассмотрим прямоугольную матрицу А m n.
Определение.
Минором матрицы А k-го порядка называется любой определитель,
составленный из элементов матрицы А, состоящих на пересечении k строк
и k столбцов, где k min(m,n).
Пример.
А3 5
1 2 3 4 5
6 7 8 9 10 .
0 0 0 0 1
У этой матрицы миноры первого порядка это: М1 = {1, 2, 3, 4, ... 10, 0},
второго порядка – М 2 {
1 2 2 3
9 10
;
;
; } ,
6 7 7 8
0 1
1 2 3
3 4
5
1 4
5
третьего порядка – М 3 { 6 7 8 ; 8 9 10 ; 6 9 10 ; } .
0 0 0
0 0
1
При этом так как k min (3, 5), то k = 3.
0 0
1
26.
Определение.Рангом матрицы называется число равное наивысшему порядку
миноров этой матрицы, отличных от нуля.
Обозначение ранга Rg (A) rang (A) r(A).
Для рассмотренной выше матрицы А3х5 ранг равен 3. Действительно r(A3 5) =
1 2
5
3, так как существует М 3 6 7 10
0 0
1
1 2
6 7
5 0.
Свойства ранга.
Ранг матрицы не изменяется:
1) При транспонировании;
2) При перестановке строк или столбцов местами;
3) При отбрасывании строки или столбца из нулей;
4) При умножении строки или столбца на число не равное нулю;
5) При удалении строки или столбца, являющегося линейной комбинацией
других строк (столбцов);
6) При добавлении к строке или столбцу линейной комбинации других строк
или столбцов.
Преобразования не изменяющие ранга матрицы называются
эквивалентными, и матрицы, получающиеся при таких преобразованиях,
называются эквивалентными также.
Обозначения эквивалентных матриц таково А В.
27.
ЗАМЕЧАНИЕ. В литературе эквивалентные преобразования могутназываться элементарными преобразованиями. Используя эквивалентные
преобразования ранг матрицы может быть определен сведением ее к
ступенчатому виду:
a 11 a 12
0 a
22
A 0
0
0
0
a 13
a 23
a 33
0
a 1r
a 2r
a 3r
a rr
a 1k
a 2k
a 3 k , aii 0, i=1,2,...r, r k.
a rk
Пример.
2 1
0 3 3 4 2 2 1 5 2
2 0
0
3
0
1
5
1
2
2
0
1 3
1 0 3 0 0 3 3 4 0
5 0
22 1
тогда существует М 3 0 2 5 84 0 , значит
0 0 21
0
3
А4 3
3
4
5 2 2 1 5
2 5 5 0 2 5 5 ,
3 3 4 0 0 21 7
2
1
r(А)=3.
28.
Назовем системой линейных уравнений (СЛУ) систему вида{
a11 x1 a12 x 2 a1n x n b1
a 21 x1 a 22 x 2 a 2 n x n b 2
(1) A X B (2)
a m1 x1 a m2 x 2 a mn x n b m
где aij – известные коэффициенты, xi – неизвестные переменные, bi –
известные свободные члены,
a 11
А
a
m1
a 12
am2
x1
b1
a 1n
x
b
; X 2 ; B 2
a mn
x
b
n
m
Решением системы называется такой набор чисел ( 1, 2,... n), который
после подстановки вместо существующих неизвестных (х1, х2, ...хn) обращает
каждое уравнение в верное равенство.
Если такой набор чисел существует, то говорят что система (1) или (2)
совместна, если нет - то не совместна.
Расширенной матрицей для систем (1) или (2) называют матрицу,
составленную из элементов матриц А и В следующего вида:
a 11
a
A p 21
a
m1
a 12
a 22
am2
a 1 n b1
a 2 n b2
a mn bm
Имеется теорема позволяющая судить о существовании решения
систем вида (1) или (2).
29.
Теорема. (Кронеккера - Капелли).Для существования решения системы (1) необходимо и достаточно,
чтобы ранг основной матрицы А равнялся рангу расширенной матрицы А р
(r(A) = r(A р )).
ЗАМЕЧАНИЕ
1) Если r(A) r(Aр), то система (1) несовместна
2) Если r(A) = r(Ap), то система (1) совместна, причем решение системы
единственно, если r(A) = r(Ap) = n – числу неизвестных, если же r(A) = r(Ap)
< n, то система имеет бесконечное множество решений.
Алгоритм применения теоремы к решению СЛУ (систем линейных
уравнений)
1) Вычисляем r(A) и r(Ap) и сравниваем их
2) Если r(A) r(Ap), то решения СЛУ нет
3) Если r(A) = r(Ap), то проверяем справедливость равенства r(A) = r(Ap) = n
4) Если равенство выполняется, то для нахождения единственного решения
применяют метод Гаусса или правило Крамера.
5) Если равенство не выполняется (r(A) = r(Ap) < n), то перестановкой
строк (столбцов) матрицы А находят любой, отличный от нуля минор
(базисный минор) так, чтобы в СЛУ первыми стояли r строк базисного
минора. При этом (m-r) оставшихся строк системы можно отбросить как не
влияющих на решение системы, а (n-r) столбцов с соответствующими
неизвестными можно перенести в правую часть системы, задав
произвольным образом свободные переменные хj. Полученную систему r
уравнений с r неизвестными можно решить к примеру методом Гаусса.
30.
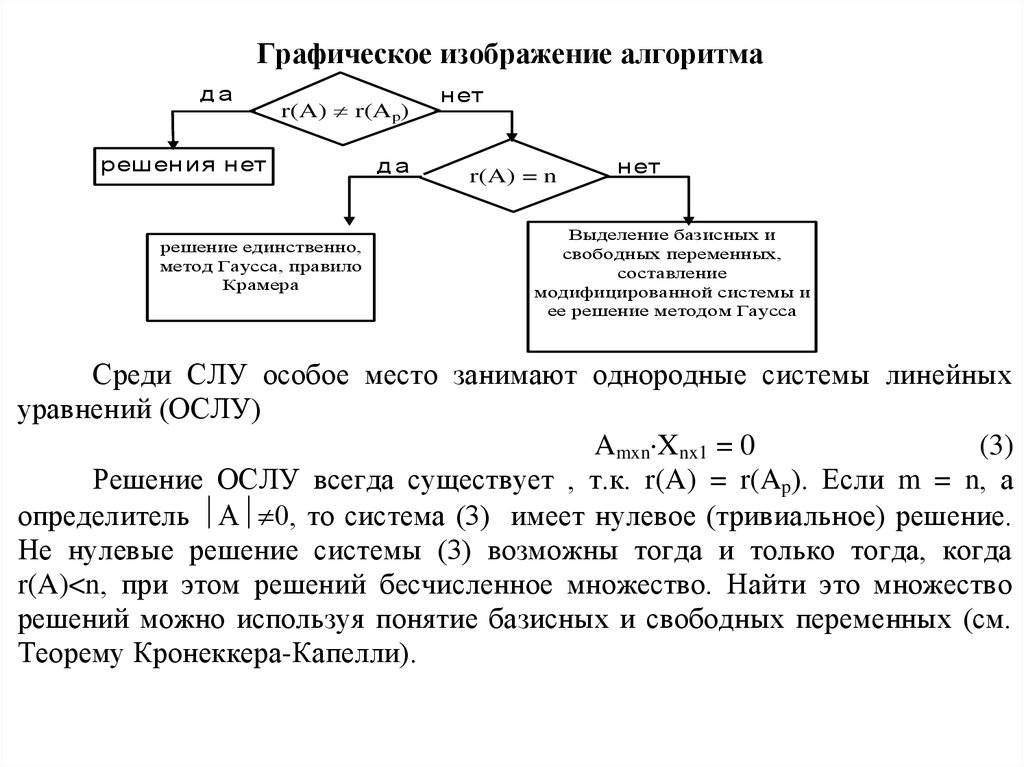
Графическое изображение алгоритмада
r(A) r(Ap)
решения нет
решение единственно,
метод Гаусса, правило
Крамера
да
нет
r(A) = n
нет
Выделение базисных и
свободных переменных,
составление
модифицированной системы и
ее решение методом Гаусса
Среди СЛУ особое место занимают однородные системы линейных
уравнений (ОСЛУ)
Amxn Xnx1 = 0
(3)
Решение ОСЛУ всегда существует , т.к. r(A) = r(Ap). Если m = n, а
определитель А 0, то система (3) имеет нулевое (тривиальное) решение.
Не нулевые решение системы (3) возможны тогда и только тогда, когда
r(A)<n, при этом решений бесчисленное множество. Найти это множество
решений можно используя понятие базисных и свободных переменных (см.
Теорему Кронеккера-Капелли).
31.
Пример.{
a 11 x1 a 12 x 2 a 13 x 3 b1
{
a 21 x1 a 22 x 2 a 23 x 3 b2
a 31 x1 a 32 x 2 a 33 x 3 b3
~
a~11 x1 a~12 x 2 a~13 x 3 b1
~
0 a~22 x 2 a~23 x3 b2
~
0 0 a~ x b
33
3
3
Переход к равносильной треугольной системе называют прямым ходом
метода Гаусса. Выражая из треугольной системы
~
b3
x3 ~ ,
a 33
затем
1
~
x 2 ~ ( b2 a~23 ~
x 3 ) , затем
a 22
1
~
x1 ~ ( b1 a~12 ~
x 2 a~13 ~
x3 ) ,
a 11
то есть выполняя обратный ход метода Гаусса,
легко находим решение системы.
Равносильные преобразования в методе Гаусса - это линейные
комбинации строк матрицы.
Для иллюстрации метода Гаусса рассмотрим примеры.
32.
Пример.Решить систему уравнений:
2 x1 3 x 2 4 x 3 x 4 1
x x 2 x x 2
1
2
3
4
x1 2 x 2 3 x 3 2 x 4 4
2 x1 2 x 2 3 x4 4 x4 0 .
Шаг 1. Делим коэффициенты первого уравнения на коэффициент а11 0,
при этом получается равносильная система уравнений.
x1 3 x 2 2 x 3 1 x 4 1
2
2
2
x 1 x 2 2 x 3 x4 2
x1 2 x 2 3 x 3 2 x 4 4
2 x 2 x 3 x 4 x 0 .
2
4
4
1
Шаг 2. На месте 2 и 3 уравнений поставим сумму 1-го уравнения,
умноженного на (-1), и 2,3- уравнений. На месте 4-го уравнения сумму 1-ой
строки, умноженную на (-2), и 4-ой строки. Для краткости записей
воспользуемся понятием расширенной матрицы и эквивалентных
преобразований
1
1
1
2
1 1
2
2
2
1
2
1 2 0
2
3 2
4 0
2
3
4
0 0
3
2
1
3
2
1
2
7
2
1
1
2
3
0
2
2
3
7
5
2
2
1 3
1
2
1
2
3
Т. к. во 2, 3, 4 уравнениях неизвестное х1- исключено, то применим
схему приведенную выше для исключения неизвестных в системе, состоящей
из 2, 3, 4 уравнений. Для этого вторую строку разделим на 1/2, на месте 3,
поставим сумму элементов 2 строки, умноженную на (-7/2), и 3-й строки на
месте 4-ой строки сумму элементов 2 строки умноженную на (-1) и 4 строки.
33.
10
0
0
Исключая неизвестные в
прямой ход метода Гаусса.
1
2
2
2
0
3 3
5 12 7
1 6
4
4 уравнениях по той же схеме завершим
3
1
0
0
3 и
2
1
1
1
1 3
2
2
2
2
0
1
0
3
3
7
12
0
0
1
5
5
0
0
0 18
13
5
5
Используя обратный ход метода Гаусса, имеем:
13
,
18
7 12 13
1
x3
5 5 18
3
13 5
x2 3 3
18 6
1 3 5 2 13 25
x1 .
2 2 6 3 36 9
x4
.
34.
Лекция 4. Определение линейногопространства. Аксиомы, линейная зависимость и
независимость векторов. Базис и размерность
линейного пространства; преобразование
координат вектора при переходе к новому
базису. Скалярное произведение векторов,
норма вектора, неравенство КошиБуняковского, ортонормированиый базис.
Линейный оператор, его матрица. Матрица
линейного оператора при переходе к новому
базису. Собственные векторы, их нахождение.
Квадратичные формы, приведение их формы к
каноническом) виду.
35.
1. Линейные пространстваОпределение.
Множество L х, у, z, ... элементов любой природы называется
линейным пространством над полем действительных чисел R, если
выполняются три условия:
1 ) в множестве L определена операция сложения , которая каждым
двум элементам х, у L ставит в соответствие единственный третий
элемент
z L ( обозначаемый z x y и называемый их суммой );
2 ) в множестве L определена операция умножения на элементы поля
R , которая каждому элементу х L и каждому элементу R
ставит в соответствие единственный элемент
L ( обозначаемый
х и называемый произведением действительного числа на х );
3 ) операции сложения и умножения на действительное число
удовлетворяют следующим восьми аксиомам:
1) х у у х для х, у L ;
2) (х у) z х (у z) для х , у , z L ;
36.
1) существует2)
5)
6)
7)
8)
о L (называемый нулевым элементом в L) такой, что х
о = х для х L ;
для х L существует единственный элемент (-х) L
( называемый противоположным для х) такой, что х (-х )= о;
1 х = х для х L ;
( х) ( ) х для х L и , R ;
(х у) х у для х, у L и R ;
( ) х х х для х L и , R .
Аксиомы 1) – 4) называются аксиомами сложения, аксиомы
5) , 6) –
аксиомами умножения, аксиомы 7) , 8) - аксиомами
дистрибутивности .
Элементы всякого линейного пространства обычно называют векторами
х , у , z … , а само линейное пространство называют
и обозначают
векторным пространством.
Заметим, что в определении линейного пространства не говорится, каким именно образом определены
операции сложения и умножения на действительное число. Существенно лишь то, что они должны
удовлетворять перечисленным выше аксиомам 1) – 8).
37.
2. Линейная зависимость векторов линейного пространства.Рассмотрим произвольное линейное пространство L . Здесь
и в
дальнейшем операции сложения « » и умножения на число « » в нем
будем обозначать проще: « + » и « ».
Пусть е1 , е 2 , ... , е n - некоторые элементы этого пространства.
Определение.
1 , 2 , ... , n R ,
Выражение вида 1 е1 2 е 2 ... n е n , где
называется линейной комбинацией векторов
е1 , е 2 , ... , е n , а числа 1 , 2 , ... , n называются коэффициентами этой
линейной комбинации.
Определение. Система векторов ( е1 , е 2 , ... , е n ) линейного пространства
L называется линейно независимой, если их линейная комбинация равна
нулевому элементу пространства в том и только в том случае, когда
1 2 ... n 0 . В противном случае,
т.е. когда равенство
1 е1 2 е 2 ... n е n = о возможно и при условии, что хотя бы один
из коэффициентов 1 , 2 , ... , n отличен от нуля, векторы е1 , е 2 , ... , е n
называются линейно зависимыми.
Итак, для линейно независимой системы векторов:
1 0
0
1 е1 2 е 2 ... n е n = o 2
...
n 0 .
38.
3. Размерность линейного пространства. Базис. КоординатыОпределение. Линейное пространство L называется n -мерным, если в
нем существует n линейно независимых векторов, а любые ( n+1 ) векторы
этого пространства линейно зависимы.
Определение . Базисом n-мерного пространства L называется любая
упорядоченная система из n
линейно независимых векторов этого
пространства.
Основная теорема о базисе:
Любой вектор пространства L может быть единственным образом
разложен по базису Е (е1 , е 2 , ... , е n ) этого пространства, и при этом, если
x 1 е1 2 е 2 ... n е n
, то числа 1 , 2 , ... , n называются
координатами вектора x в базисе Е.
Теорема, обратная теореме о базисе:
Если в пространстве L существует n линейно независимых векторов
( е1 , е 2 , ... , е n ) таких, что любой вектор х L линейно выражается через е1 , е 2 , ... , е n , то
пространство является n-мерным, а система ( е1
, е 2 , ... , е n ) – одним из его базисов.
39.
4. Матрица перехода от одного базиса к другому.Пусть Е е1 ; е2 ; ... , еn - некоторый базис в линейном пространстве L.
И пусть Е е1 ; е2 ; ... , еn - какой-либо другой базис в этом же
пространстве.
Матрицей перехода от базиса Е к базису Е´ называется матрица Т, столбцами
которой являются координаты векторов е i ( i 1,2,.., n ) в базисе Е.
Пусть х - некоторый вектор из линейного пространства L.
х1
х
Х 2 - координаты этого вектора в базисе Е.
...
х
n
х
1
х
Х 2 - координаты этого вектора в базисе Е .
...
х
n
1
Тогда имеет место формула: Х Т
Х.
40.
5. Линейный операторПусть каждому элементу х из линейного пространства L некоторое
преобразование А ставит в соответствие элемент А(х) из этого же
пространства.
Определение. Преобразование А называется линейным, если:
1) для любых элементов х1 L и х 2 L выполняется равенство
А(х1 х 2 ) А(х1 ) А(х 2 ) ;
(1)
2) для любого числа R и любого элемента x L выполняется равенство
А ( х ) А ( х ) .
(2)
Замечания.
1) Линейное преобразование называется также линейным оператором.
2) В обозначении А(х) скобки обычно опускаются.
41.
6. Преобразование матрицы оператора при переходе к новомубазису
Пусть в линейном пространстве L
дан некоторый
E (е1 ; е2 ; ... ; еn ) и некоторый линейный оператор А .
Найдем образы базисных векторов под действием оператора А :
Ае1 a11 е1 a21 е2 ... an1 еn
базис
Ае2 a12 е1 a22 е2 ... an 2 еn
. . . . . . . . . . .
Аеn a1n е1 a2n е2 ... ann еn .
Тогда матрица, столбцами которой являются координатные столбцы
a11 a12 . . .a1n
a21 a22 . . .a2 n
.
. образов базисных векторов: .
an1 an 2 . . .ann
называется матрицей оператора А в базисе Е и обозначается А E . При этом,
если xE представляет собой столбец координат вектора x L , то столбец
координат образа этого вектора будет находиться по формуле:
y E AE xE .
(1)
Пусть Е - какой-либо другой базис пространства L , Т - матрица перехода
от базиса Е к базису Е . Тогда матрица оператора А в базисе Е
вычисляется по следующей формуле:
AE T 1 AE T
.
(2)
42.
7. Действия над линейными операторамиРассмотрим множество линейных операторов, действующих в линейном
пространстве L.
Определение 1. Суммой двух операторов А и В называется такой
оператор С , который на любой вектор х пространства L действует по
следующему правилу: Сх Ах Вх .
В этом случае пишут: С А В .
Определение 2. Произведением некоторого действительного числа на
оператор А называется такой оператор Д , который на каждый вектор х
пространства L действует по следующему правилу
В этом случае пишут: Д А .
Д х ( А х) .
Оператором, противоположным к оператору А ,
называется такой оператор ( А ) , который на каждый вектор х пространства
Определение 3.
L действует по следующему правилу: ( А)х ( 1) А х .
В этом случае пишут: А ( 1) А .
Определение 4. Произведением операторов А и В называется такой оператор F , который на каждый
вектор х пространства L действует по следующему правилу: F x ( А B) x A (B x) .
43.
Рассмотрим некоторый базис Е е1 ; е 2 ; ... , еn в линейном пространствеL. Каждому линейному оператору соответствует матрица в выбранном
базисе (см. пункт 6). Пусть А и В - линейные операторы в линейном
пространстве L.
Справедлива следующая теорема:
1) При сложении линейных операторов их матрицы складываются;
2) При
умножении
линейного
оператора
на
число его матрица
умножается на это число;
3) Произведению операторов
оператора
А
А B соответствует матрица, равная произведению матрицы
на матрицу оператора
В.
44.
8.Образ и ядро линейного оператораПусть
в линейном пространстве L задан некоторый линейный
оператор А .
Определение 1. Множество векторов
Ах | x L
называется образом
(областью значений) оператора А , действующего в этом пространстве, и
обозначается JmA .
Определение 2. Множество всех векторов х L таких, что Ах 0 ,
называется ядром оператора и обозначается Ker А .
45.
Чтобы найти матрицу оператора В в базисе E (i ; j ; k ) , найдемобразы базисных векторов. Учитывая, что поворот векторов происходит
вокруг оси Ох, образом вектора i является вектор i , значит,
Вi 1 i 0 j 0 k .
Образом вектора j в результате действия оператора В является вектор с
координатами (0; cos ; sin ) , а образом вектора k - вектор с координатами (
0; sin ; cos ) (см. рис. 5) , т.е.
B j 0 i cos j sin k
z
k
Bk 0 i sin j cos k .
Bj
Теперь составим матрицу оператора В
Bk
(см. пункт 6):
0
i
x
Рис.5
j
у
1
0
0
0
cos sin .
sin
cos
0
46.
Пусть произвольный вектор x имеет координаты (x1 ; x 2 ; x 3 ) . По формуле(1) из пункта 6 вычислим столбец координат образа этого вектора:
1
0
0
0
cos
sin
x1
x1
sin x 2 х 2 cos х 3 sin
cos x 3 х 2 sin х 3 cos
0
, т.е.
Bx x1 i (x 2 cos x 3 sin ) j (x 2 sin x 3 cos )k .
Тогда образом оператора В является множество
Jm B x1 i (x 2 cos x 3 sin ) j (x 2 sin x 3 cos )k | x1 , x 2 , x 3 R .
Покажем, что это множество есть множество V 3 , т.е. каждый вектор V 3
является образом некоторого вектора x .
Пусть y - произвольный вектор пространства V 3 с координатами
(y 1 ; y 2 ; y 3 ) . Докажем, что существует вектор x V 3 такой, что B x y .
Это равносильно следующему равенству:
47.
x1 i (х 2 cos х 3 sin ) j (х 2 sin х 3 cos )kx1 y 1
y 1 i y 2 j y 3 k х 2 cos х 3 sin y 2
х sin х cos y
3
3
2
А эта система является совместной, т.к. ее главный определитель
1
0
0
0
cos sin 1 0 .
0 sin
cos
Таким образом, единственное решение этой системы
x
1
; x2 ; x3
является координатами искомого вектора x .
Для нахождения ядра оператора В решим уравнение
B x о x1 i (х 2 cos х 3 sin ) j (х 2 sin х 3 cos )k
x1 0
0 i 0 j 0 k х 2 cos х 3 sin 0
х sin х cos 0 .
3
2
Очевидно, что эта однородная система имеет только нулевое решение:
x1 0
x 2 0
x 0 .
3
Поэтому ядро оператора В состоит лишь из нулевого вектора:
.
Ker B 0 i 0 j 0 k о
48.
9. Собственные векторы и собственные числа линейногооператора
Пусть L – некоторое линейное пространство, А - линейный оператор,
действующий в этом пространстве.
Определение. Ненулевой вектор х называется собственным вектором
линейного оператора А с собственным числом , если Ах х
(1),
где - некоторое действительное число.
Пусть А – матрица оператора А , Е – единичная матрица того же размера,
Х – столбец координат вектора x , 0 – нулевой столбец.
Тогда А х х ( А Е) Х 0 , где Х 0 .
(2)
Отсюда следует, что число будет собственным числом оператора А в
том и только в том случае, когда А Е 0 .
(3)
Уравнение (3) называется характеристическим уравнением для
матрицы А. Итак, - собственное число А тогда и только тогда, когда
является корнем характеристического уравнения для матрицы А. Столбец
координат Х любого собственного вектора, соответствующего собственному
числу , есть некоторое нетривиальное решение однородной системы (2).
49.
10. Квадратичные формыОпределение. Квадратичной формой действительных
х1 , х 2 , ... , х n
называется
однородный
многочлен
переменных
второй
степени
относительно этих переменных, т.е. многочлен, не содержащий свободного
члена и членов первой степени.
n n
Квадратичная форма имеет вид f (x1 , x 2 , ... , x n ) a ij x i x j , где
i 1 j 1
a ij a ji - коэффициенты квадратичной формы.
Например, при n =2:
f (x1 , x 2 ) a11 x12 a12 x1 x 2 a 21 x 2 x1 a 22 x 2 2
a11 x12 2a12 x1 x 2 a 22 x 2 2 ;
при n=3:
f (x1 , x 2 , х 3 ) a11 x12 a 22 x 2 2 a 33 x 3 2 2a12 x1 x 2 2a13 x1 x 3
2a 23 x 2 x 3 .
50.
Симметрическую матрицу ( a ij a ji )a11 a12 ... a1n
a 22 ... a 2n
a
А 21
.
.
.
a
n1 a n 2 ... a nn
,
составленную из коэффициентов квадратичной формы, называют матрицей
квадратичной формы.
Квадратичная форма называется канонической
(иначе говоря, имеет канонический вид), если все a ij 0 при i j .
Нахождение
канонической
по
данной
квадратичной
квадратичной
формы,
форме
эквивалентной
называется
ей
приведением
квадратичной формы к каноническому виду.
Преобразования, приводящие квадратичную форму к каноническому
виду, могут быть найдены методом Якоби, Лагранжа, ортогональным
преобразованием или другими.
Рассмотрим некоторые из них.
Метод Лагранжа –приведения квадратичной формы к каноническому
виду – состоит в последовательном выделении в квадратичной форме полных
квадратов.
51.
Следует иметь в виду, что канонический вид квадратичной формытак же, как и линейное невырожденное преобразование, которое
приводит квадратичную форму к каноническому виду,
определяется неоднозначно. Однако при этом справедлив закон
инерции
квадратичной
формы:
число
слагаемых
с
положительными каноническими коэффициентами и число
слагаемых с отрицательными каноническими коэффициентами
постоянно и не зависит от линейного невырожденного
преобразования,
приводящего
квадратичную
форму
к
каноническому виду.
Замечание. Если в записи квадратичной формы f (x1 , x 2 , ... , x n )
отсутствует переменная x k (k n) , т.е. a mk 0 (1 m n) , то,
записывая преобразование переменных, надо положить x k x k
52.
11. Приведение квадратичной формы к каноническому виду припомощи ортогонального преобразования.
Ввиду того, что матрица квадратичной формы является симметрической
(т.к. a ij a ji ), то корни 1 , 2 , ... , n ее характеристического уравнения
являются действительными числами
( см. свойства симметрической
матрицы). Пусть e1 , e 2 , ... , e n
- ортогональные нормированные
собственные
векторы, соответствующие характеристическим числам
1 , 2 , ... , n , в ортогональном базисе l e1 , e 2 , ... e n .
В свою очередь, векторы
e1 , e 2 , ... , e n образуют некоторый
ортонормированный базис. Разлагая вектор e i
по базису Е , составим
Т
матрицу перехода от базиса Е к базису E ( E E ), и формулы
преобразования
координат
векторов
при
переходе
к
новому
ортонормированному базису из собственных векторов будут иметь вид:
x E T x E .
Преобразовав при помощи этих формул квадратичную форму
f (x1 , x 2 , ... , x n ) , получим квадратичную форму
f (x , x , ... , x ) (x ) 2 (x ) 2 ... (x ) 2 ,
1
2
n
1
1
2
2
не содержащую членов с произведениями x i x j , где i j .
n
n
Принято говорить, что квадратичная форма при этом приведена к каноническому виду при помощи
ортогонального преобразования.
53.
Согласно сказанному, приведение квадратичной формы к каноническомувиду может быть осуществлено по следующему плану.
Пусть в некотором базисе E e1 , e 2 , ... e n дана квадратичная форма
а11 а12 а1n
a 21 a 22 a 2n
f (x1 , x 2 , ... , x n ) с матрицей А
.
.
.
.
a
a
a
n
1
n
2
nn
1.Составляем характеристическое уравнение матрицы А:
a11
a12 ... a1n
a 21
.
a n1
a 22 ... a 2n
.
.
a n2
0 и находим его корни 1 , 2 , ... , n .
a nn
2.Находим n собственных векторов с собственными числами 1 , 2 , ... , n
так, чтобы эти векторы были ортогональны друг к другу
( это всегда
возможно, так как преобразование является симметрическим, и, кроме того,
собственные векторы симметрического оператора, соответствующие
различным собственным числам, уже взаимно ортогональны ), обозначим их
e
,
e
,
...
,
e
соответственно через 1
2
n .
54.
1.Переходим к базису из собственных векторов. В этом базисе матрицалинейного преобразования будет иметь диагональный вид:
1
0
А
.
0
0
0
.
n
0
2
.
0
и данная квадратичная форма получает канонический вид:
f (x , x , ... , x ) (x ) 2 (x ) 2 ... (x ) 2 .
1
2
n
1
1
(при переходе к базису
2
E
2
n
n
координаты всех векторов преобразуются
согласно матричному равенству x E T x E , где Т – матрица перехода от
базиса Е к базису E ).



















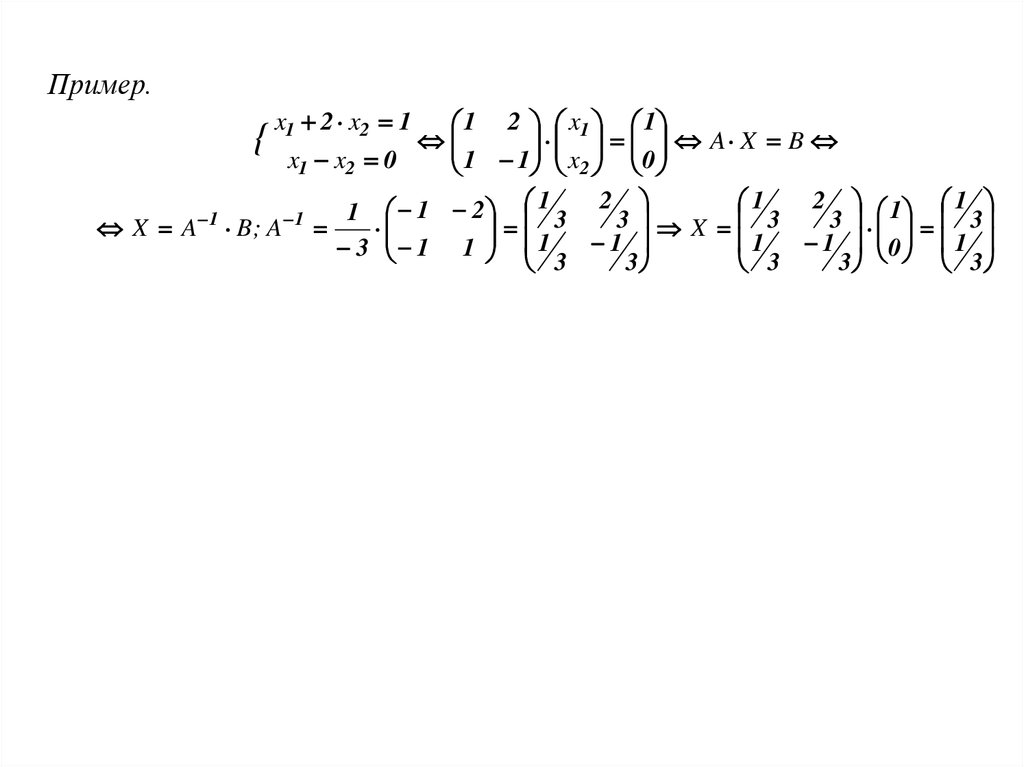

































 Математика
Математика








