Похожие презентации:
Обратная матрица. Матричный способ решения линейной системы уравнений. Формулы Крамера
1.
Лекция №2.Обратная матрица.
Матричный способ
решения линейной
системы уравнений.
Формулы Крамера.
2. Квадратная матрица A-1 порядка n называется обратной матрицей для данной матрицы A, если A·A-1=A-1·A=E(единичная матрица)
Если Δ≠0, то матрица A A11, A12, …, Ann алгебраическиенеособенная
дополнения
(невырожденная).
Если Δ=0, то матрица A соответствующих
элементов матрицы.
особенная
(вырожденная).
Всякая неособенная
A11 A21 ... An1
матрица A имеет
1 A12 A22 ... An 2
-1
обратную матрицу A = ... ... ... ...
A
1n
A2 n
...
Ann
3. Найти матрицу A-1, если
12
0
0
3
1 1
0
1
2
3
1
1
2
0
2
0
1
2
0
2
0
3
1
3
1
1
2
1 2 0
A 0 3 1 .
0 1 2
5 0
=> матрица A невырожденная и имеет обратную матрицу A-1.
A11
3
1
5 A21
2 0
1
1 2
1
0 1
A
A12
0 22
0
0 2
A13
0
3
0
1
0A
23
2
0
2
4
A31
2 A32
1
2
0
1
A 1
2 0
3 1
1
0
1
5
1
0
5
0
2
A33
4
2
1
0
1
1
1
2
0
3
3.
1
2
1 0
3
0
4
5
2
5
1
5
2
5
1
.
5
3
5
4.
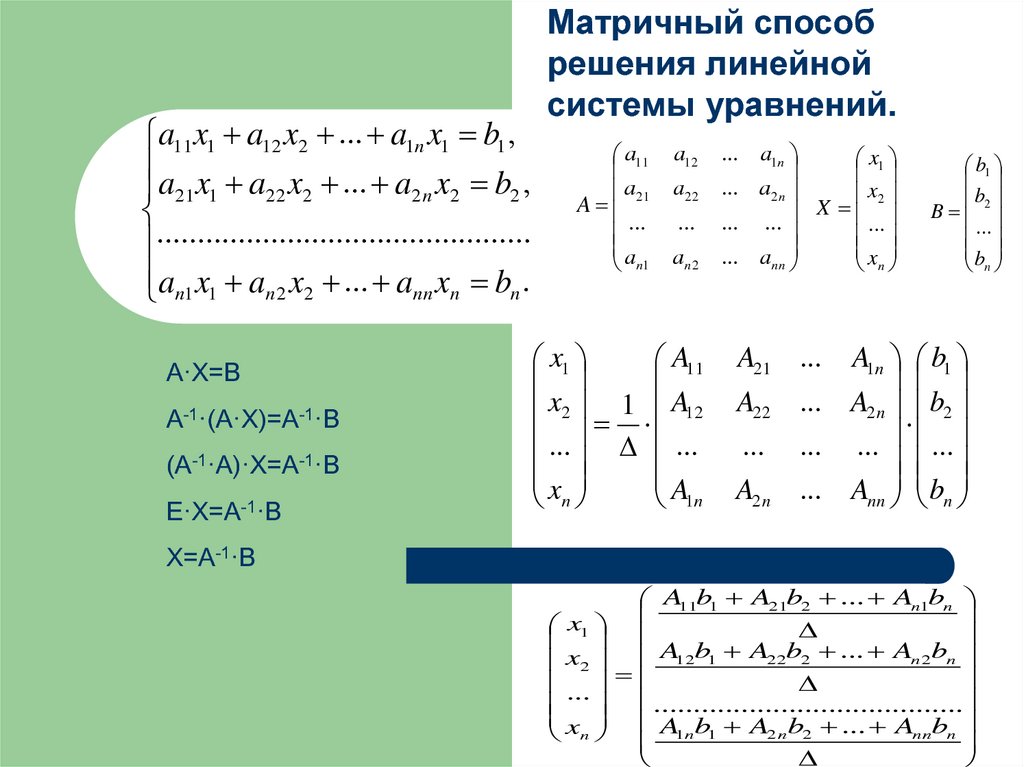
a11 x1 a12 x2 ... a1n x1 b1 ,a x a x ... a x b ,
21 1 22 2
2
2n 2
..............................................
an1 x1 an 2 x2 ... ann xn bn .
A·X=B
A-1·(A·X)=A-1·B
(A-1·A)·X=A-1·B
E·X=A-1·B
Матричный способ
решения линейной
системы уравнений.
a11 a12
a22
a
A 21
... ...
a
n1 an 2
x1
A11
x2 1 A12
... ...
x
A
n
1n
... a1n
x1
... a2 n
x2
X
...
... ...
x
... ann
n
b1
b
B 2
...
b
n
A1n b1
... A2 n b2
... ...
...
... Ann bn
A21 ...
A22
...
A2 n
X=A-1·B
x1
x
2
...
x
n
A11b1 A21b2 ... An1bn
A
b
A
b
...
A
b
22 2
n2 n
12 1
.......................................
A1n b1 A2 n b2 ... Annbn
5. Матричный способ решения линейной системы уравнений.
a11 x1 a12 x2 ... a1n x1 b1 ,a x a x ... a x b ,
21 1
22 2
2n 2
2
..............................................
an1 x1 an 2 x2 ... ann xn bn .
A11b1 A21b2 An1bn
x1
x2
A12b1 A22b2 An 2bn
......................................................
xn
A1nb1 A2 nb2 Annbn
6. Решить матричным способом систему уравнений
Решить матричным способомx 2 y z 4,
систему уравнений
2 x y 2z 3,
3x y 2z 2.
1
2
2 1
3
A
1
1
1
2
1
0 5
2 0 5
2
A11
1
A12
A13
A 1
1
3
A 21
A 22
A 23
1
2
A 31
A 32 .
A 33
5
0 5
1
10 5 0 .
25
5 5 5
1
1
3 2
A11
25 0
1
2
1
2
2
2
0,
1
1 2
x
4
A 2 1 2 , X y , B 3 .
3 1 2
z
2
A 21
2
1
5,
A 31
2
1
5,
1 2
1 2
1 1
1 1
A12
10, A 22
5, A 32
0,
3 2
3 2
2 2
2 1
1 2
1 2
A13
5,
A 23
5, A 33
5.
3 1
3 1
2 1
5 4
x
0 5
25 1
1
1
10 5 0 3
25 1
y
25
25
z
5 5 5 2
25 1
x 1, y 1, z 1.
7. Формулы Крамера.
a11 x1 a12 x2 ... a1n x1 b1 ,a x a x ... a x b ,
21 1 22 2
2n 2
2
..............................................
an1 x1 an 2 x2 ... ann xn bn .
Формулы Крамера.
a11 a12 ... a1n
a21 a22 ... a2 n
...
... ... ...
an1 an 2 ... ann
x1
b1
a12 ... a1n
b2
a22 ... a2 n
...
...
bn
an 2 ... ann
x1
...
x1
...
a11 a12 ... b1
a11 b1 ... a1n
x2
a21 b2 ... a2 n
...
... ...
...
an1 bn ... ann
x2
x2
…
…
xn
a21 a22 ... b2
...
... ... ...
an1 an 2 ... bn
xn
xn
8. Решить по формулам Крамера систему уравнений
Решить по формулам Крамера системуx 1 4x 2 9,
5x 1 x 2 3.
уравнений
1
4
5 1
21.
X1
9
4
X2
1
9
5
3
3 1
21
42
x1
x2
X1
X2
21 1
21
42
2
21
9.
Ранг матрицы.Теорема Кронекера-Капелли.
Метод Гаусса.
10. Квадратная матрица A-1 порядка n – обратная матрица для данной матрицы A, если A-1 = A-1 A=E – единичная матрица
Если Δ≠0, то матрица A неособенная(невырожденная).
Если Δ=0, то матрица A особенная
(вырожденная).
Всякая неособенная матрица A
имеет обратную матрицу A-1=
A11
1 A
12
...
A
1n
A21
...
A22
...
...
...
A2 n
...
An1
An 2
...
Ann
11. Выделить в матрице k строк и k столбцов (k≤min(m,n)) Из элементов, стоящих на пересечении выделенных строк и столбцов составить
a11a21
A
...
a
m1
a12
a22
...
am 2
... a1n
... a2 n
... ...
... amn
Выделить в матрице k строк и k столбцов (k≤min(m,n))
Из элементов, стоящих на пересечении выделенных строк и
столбцов составить определитель k-го порядка.
Ранг матрицы r(A) – наибольший из порядков миноров данной
матрицы, отличных от нуля.
0≤r(A)≤min(m;n)
Минор, порядок которого определяет ранг матрицы – базисный.
12.
Свойства ранга матрицыПри транспонировании матрицы её ранг
не меняется
Если вычеркнуть из матрицы нулевой
ряд, то ранг матрицы не изменится.
Ранг матрицы не изменится при
элементарных преобразованиях матрицы.
13.
Система, имеющая хотя бы однорешение, называется совместной.
Система, имеющая только одно решение,
называется определённой.
Система, имеющая более одного решения
называется неопределённой.
Система, не имеющая ни одного решения
называется несовместной.
14.
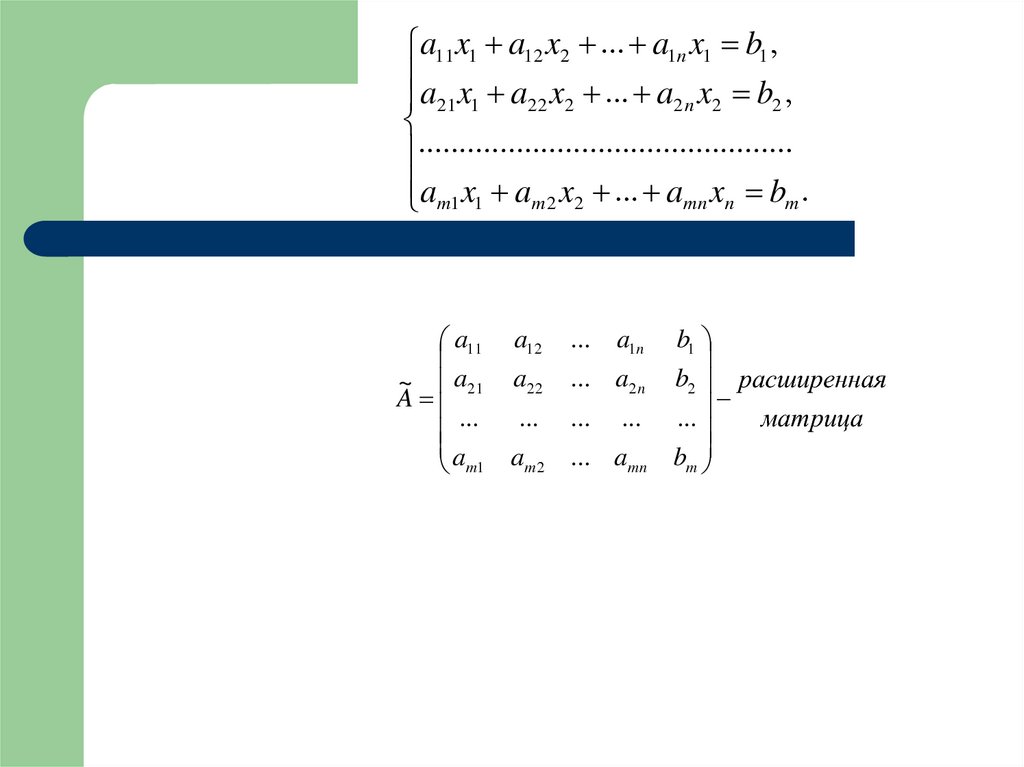
a11 x1 a12 x2 ... a1n x1 b1 ,a x a x ... a x b ,
21 1 22 2
2n 2
2
..............................................
am1 x1 am 2 x2 ... amn xn bm .
a11
~ a
A 21
...
a
m1
a12
... a1n
a22
... a2 n
...
...
...
am 2 ... amn
b1
b2 расширенная
...
матрица
bm
15.
Теорема Кронекера-Капели: система линейныхалгебраических уравнений совместна тогда и только
тогда, когда ранг расширенной матрицы системы
равен рангу основной матрицы.
Теорема: Если ранг совместной системы равен числу
неизвестных, то система имеет единственное
решение.
Теорема: Если ранг совместной системы меньше
числа неизвестных, то система имеет бесчисленное
множество решений.
16. Правило решения произвольной системы линейных уравнений.
Найти ранг основной и расширенной матриц системы. Еслиr(Ã)≠r(A), то система несовместна.
Если r(Ã)=r(A)=r, то система совместна. Найти какой-либо
базисный минор порядка r. Взять r уравнений, из коэффициентов
которых составлен базисный минор. Неизвестные, коэффициенты
которых входят в базисный минор, называют главными и
оставляют слева, а остальные n-r неизвестных называют
свободными и переносят в правые части уравнений.
Найти выражения главных неизвестных через свободные.
Получить общее решение системы (множество всех решений).
Придавая свободным неизвестным произвольные значения,
получим соответствующие значения главных неизвестных.
Таким образом можно найти частные решения исходной системы
уравнений.
17.
Метод Гауссаa11 x1 a12 x2 ... a1n x1 b1 ,
a x a x ... a x b ,
21 1 22 2
2n 2
2
..............................................
am1 x1 am 2 x2 ... amn xn bm .
Исключим с помощью первого
уравнения неизвестную x1 из
остальных уравнений:
a1n
a12
b1
a11
a x1 a x2 ... a xn a ,
11
11
11
11
a
a
a11
a22
a12
b
a21
x1
x1
x2
x2 ... 2 n xn 1n xn 2 ,
a11
a21
a11
a21
a11
a21
a21
......................................................................................
a11k xk ...
am 2
amn
a1n
bm
a11
a12
am1
a x1 a x1 a x2 a x2 ... a xn a xn a .
11
m1
11
m1
11
m1
m1
1
x1 a12
x2 ... a11n xn b11 ,
1
1
1
a22 x2 ... a2 n xn b2 ,
..............................................
a1 x ... a1 x b1 .
mn n
m
m1 2
Получим:
Аналогично исключим с помощью
второго уравнения неизвестную x2
из остальных уравнений и т. д.
Получим:
1
x1 a12
x2 ... a11k xk ... a11n xn b11 ,
2
2
2
x2 ... a2 k xk ... a2 n xn b2 ,
..............................................
x ... a k x b k .
kn n
k
k
18.
a11 x1 a12 x2 ... a1n x1 b1 ,Если a21 x1 a22 x2 ... a2 n x2 b2 ,
m n ..............................................
am1 x1 am 2 x2 ... amn xn bm , то
1
1
x1 a12
x1 a12
x2 ... a11k xk ... a11n xn b11 ,
x2 ... a11n xn b11 ,
2
2
2
2
2
x2 ... a2 k xk ... a2 n xn b2 ,
x2 ... a2 n xn b2 ,
..............................................
............................
k
k
x ... a x b .
x bn .
kn n
k
n
k
n
И тогда: xn=bnn . Подставляя это значение в
предпоследнее уравнение системы найти
xn-1. Подставляя найденные значения в
предыдущие уравнения системы найти xn-2
и т. д. Итак, система будет иметь
единственное решение.
19.
переносимa11 x1 a12 x2 ... a1n x1 b1 , слагаемые
a x a x ... a x b ,
Если 21 1 22 2
в _ правую
2n 2
2
m n ..............................................
часть
am1 x1 am 2 x2 ... amn xn bm , уравнений,
получим :
20.
1x1 a12
x2 ... a11k xk ... a11n xn b11 ,
2
2
2
x2 ... a2 k xk ... a2 n xn b2 ,
..............................................
x ... a k x b k .
kn n
k
k
1
x1 a12
x2 ... a11k xk b11 a11k 1 xk 1... a11n xn ,
2
2
2
2
2
x2 ... a2 k xk ... a2 n xn b2 a2 k 1 xk 1 ... a2 n xn ,
..............................................
x ... a k x b k a k x ... a k x .
kn n
k
kk 1 k 1
kn n
k
Значения x1, x2, …, xk выражаются через значения
неизвестных xk+1, …, x . Такая система имеет
бесконечно много решений.


















 Математика
Математика








