2.02M

Категория:

Программирование

Похожие презентации:

N-схема моделирования

Схема работы лексического анализатора

Математические схемы моделирования информационных систем. Часть 2. Лекция 5

Схема взаимодействия объектов

Неоднозначные языки

Синтаксический анализ языков программирования. Распознаватели. Задача разбора. (Глава 4)

Основы трансляции языков программирования. Лекции 4-5. Синтаксический анализ. Грамматики. Нисходящий синтаксический анализ

Общая схема работы компилятора

Теория автоматов и формальных языков. Лекция 2

Методы компиляции. Лекция 2

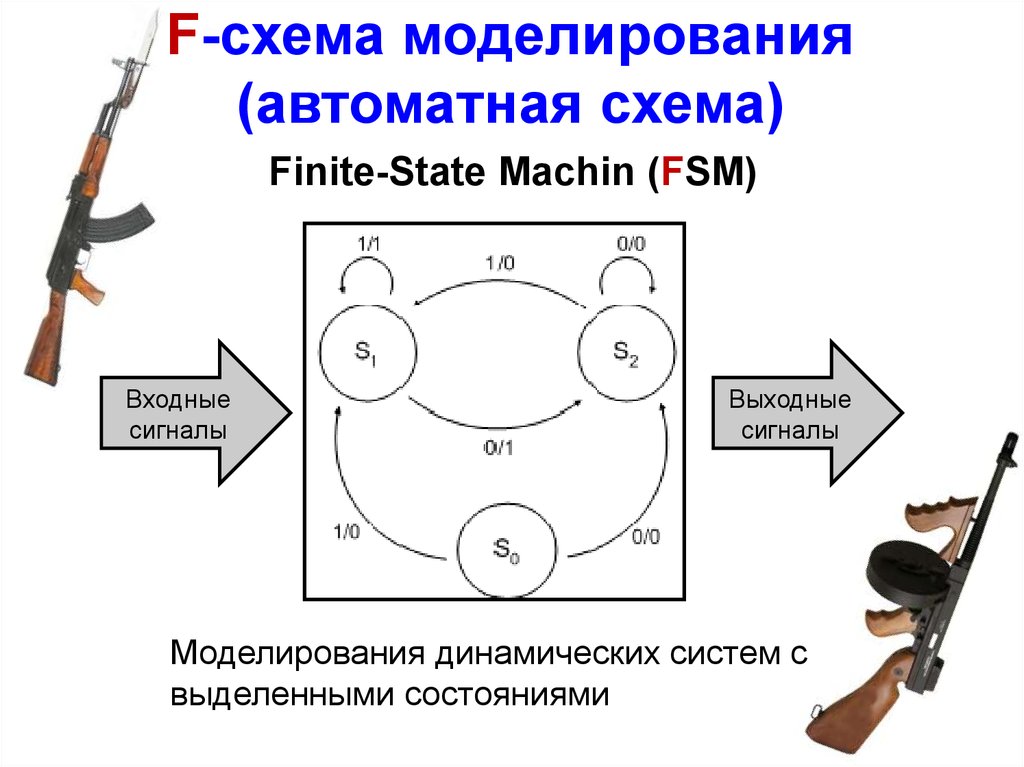
F-схема моделирования (автоматная схема)

1.

F-схема моделирования
(автоматная схема)
Finite-State Machin (FSM)
Входные
сигналы
Выходные
сигналы
Моделирования динамических систем с
выделенными состояниями

F-схема моделирования
Области применения:
1. Моделирование динамических объектов с
выделенными состояниями.
2. Моделирование систем управления
динамическими объектами
Характерные особенности F-схемы:
1. Четкое выделение состояний системы и
условий перехода из одного состояния в
другое.
2. Схема детерминированная.
3. Схема с дискретная (т.е. состояния
системы меняются в определенные
моменты модельного времени).

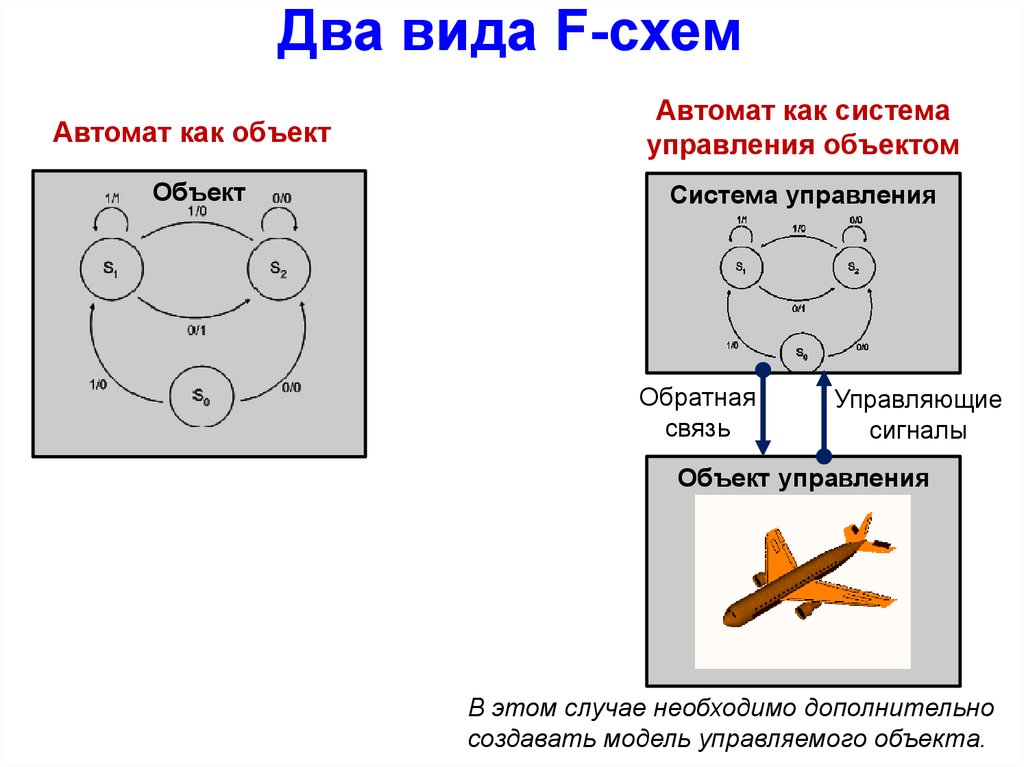
3.

Два вида F-схем
Автомат как объект
Автомат как система
управления объектом
Объект
Система управления
Обратная
связь
Управляющие
сигналы
Объект управления
В этом случае необходимо дополнительно
создавать модель управляемого объекта.

4.

F-схема моделирования
Автомат это:
A={X,Y,Q,q0,P, }
X - алфавит входных сигналов,
Y – алфавит выходных сигналов
Q – множеств состояний,
q0 Q – начальное состояние,
P – правила перехода,
(q,x) или (q) – функция выходных сигналов.
q(t+1)=P(q(t),x(t)), т.е. новое состояние автомата
зависит от текущего состояния автомата и
входного сигнала

5.

F-схема моделирования
Диаграмма
состояний автомата
X - алфавит входных сигналов,
Q – множеств состояний,
q0 – начальное состояние,
P – правила перехода,
Y - алфавит выходных сигналов
X = {0,1},
Y = {0,1}.
Q = {S0,S1,S2},
q0 = S0,
P = (S0, 0) (S2),
(0,0)=1
…
Обозначение на диаграмма состояний: входной
символ / выходной символ (например, 0/1)

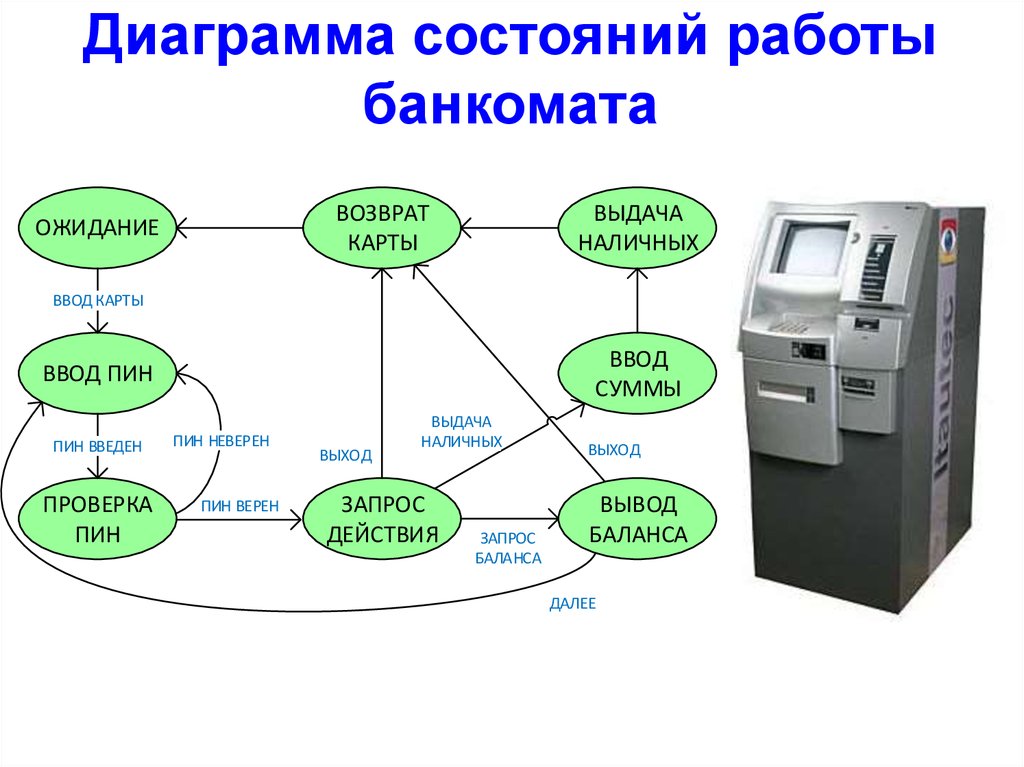
6.

Диаграмма состояний работы
банкомата
ВОЗВРАТ
КАРТЫ
ОЖИДАНИЕ
ВЫДАЧА
НАЛИЧНЫХ
ВВОД КАРТЫ
ВВОД
СУММЫ
ВВОД ПИН
ПИН ВВЕДЕН
ПРОВЕРКА
ПИН
ПИН НЕВЕРЕН
ПИН ВЕРЕН
ВЫХОД
ВЫДАЧА
НАЛИЧНЫХ
ЗАПРОС
ДЕЙСТВИЯ
ЗАПРОС
БАЛАНСА
ВЫХОД
ВЫВОД
БАЛАНСА
ДАЛЕЕ

7.

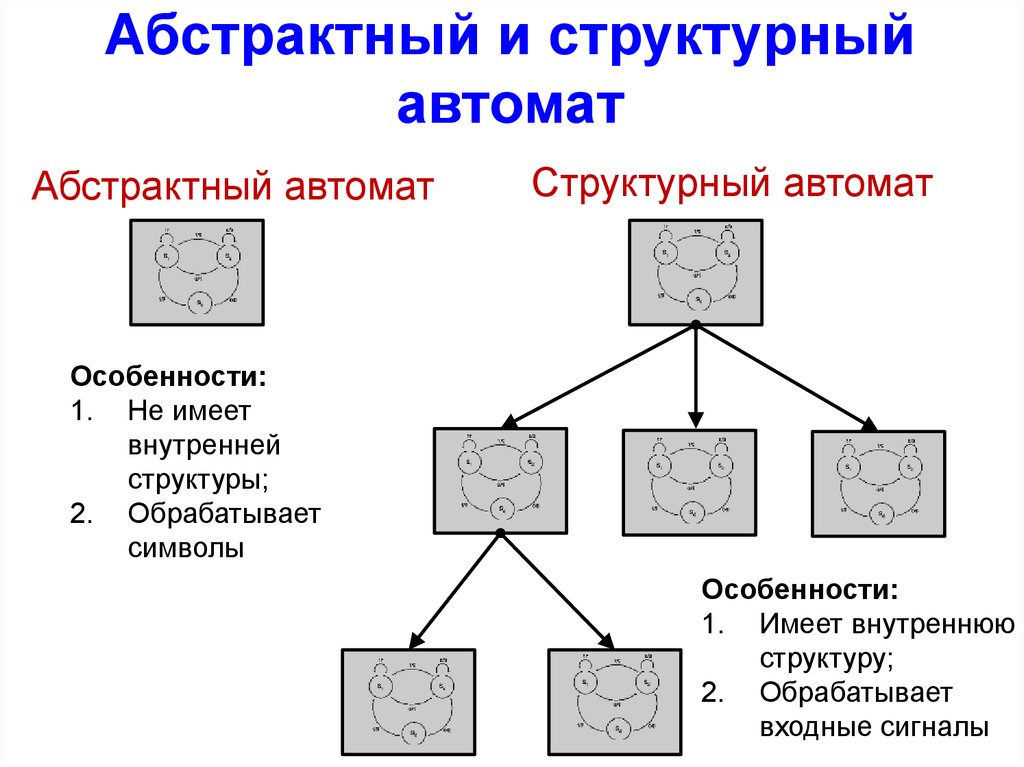
Абстрактный и структурный
автомат
Абстрактный автомат
Структурный автомат
Особенности:
1. Не имеет
внутренней
структуры;
2. Обрабатывает
символы
Особенности:
1. Имеет внутреннюю
структуру;
2. Обрабатывает
входные сигналы

8.

Абстрактный автомат
Особенности:
- Не структурирован
- В основном реализуется программно
- Принимает на вход символы
Области применения:
- Компиляция и интерпретация
искусственных языков
- Парсинг (поиск в тексте определенных
слов или языковых конструкций)
- Языковое моделирование
- Моделирование вычислительного процесса
с целью определения временной и
емкостной сложностей алгоритма

9.

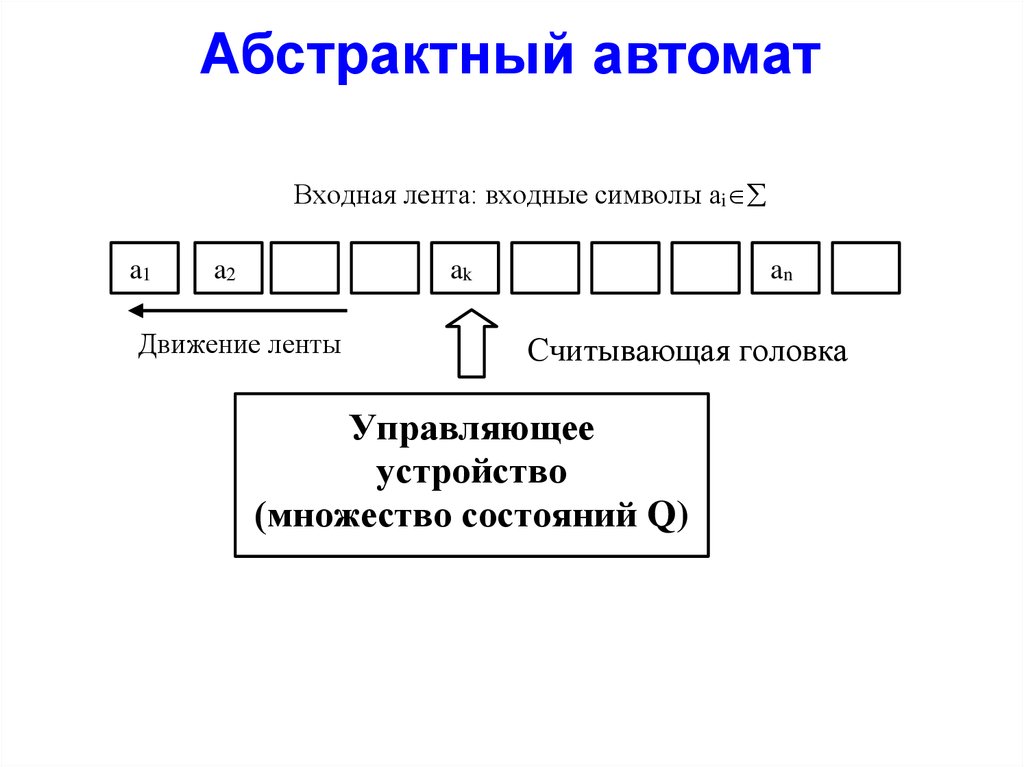
Абстрактный автомат
Входная лента: входные символы ai
a1
a2
ak
Движение ленты
an
Считывающая головка
Управляющее
устройство
(множество состояний Q)

10.

Виды абстрактных автоматов
Автомат с конечным числом состояний (КА) – автомат с
бесконечным числом состояний
Автомат-транслятор
Автомат с магазинной памятью (МП-автомат)
Детерминированный автомат – недетерминированный
автомат

11.

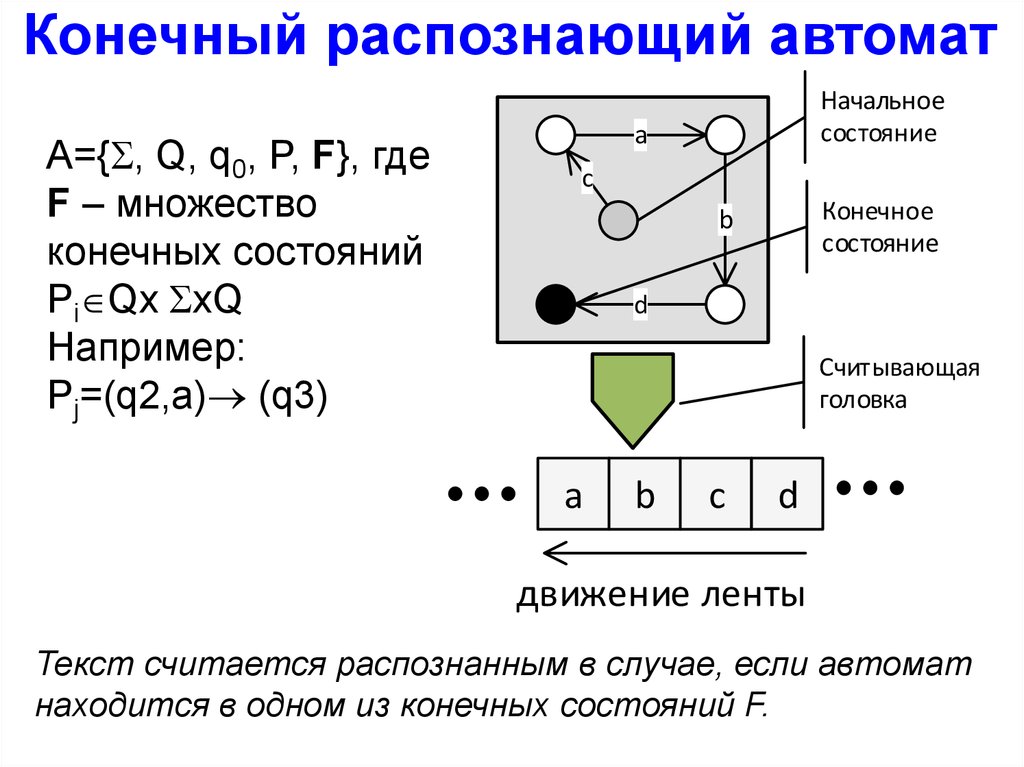
Конечный распознающий автомат
A={ , Q, q0, P, F}, где
F – множество
конечных состояний
Pi Qx xQ
Например:
Pj=(q2,a) (q3)
Начальное
состояние
a
c
Конечное
состояние
b
d
Считывающая
головка
a
b
c
d
движение ленты
Текст считается распознанным в случае, если автомат
находится в одном из конечных состояний F.

12.

Пример диаграммы состояний
конечного автомата
Конечное
состояние
Начальное
состояние

13.

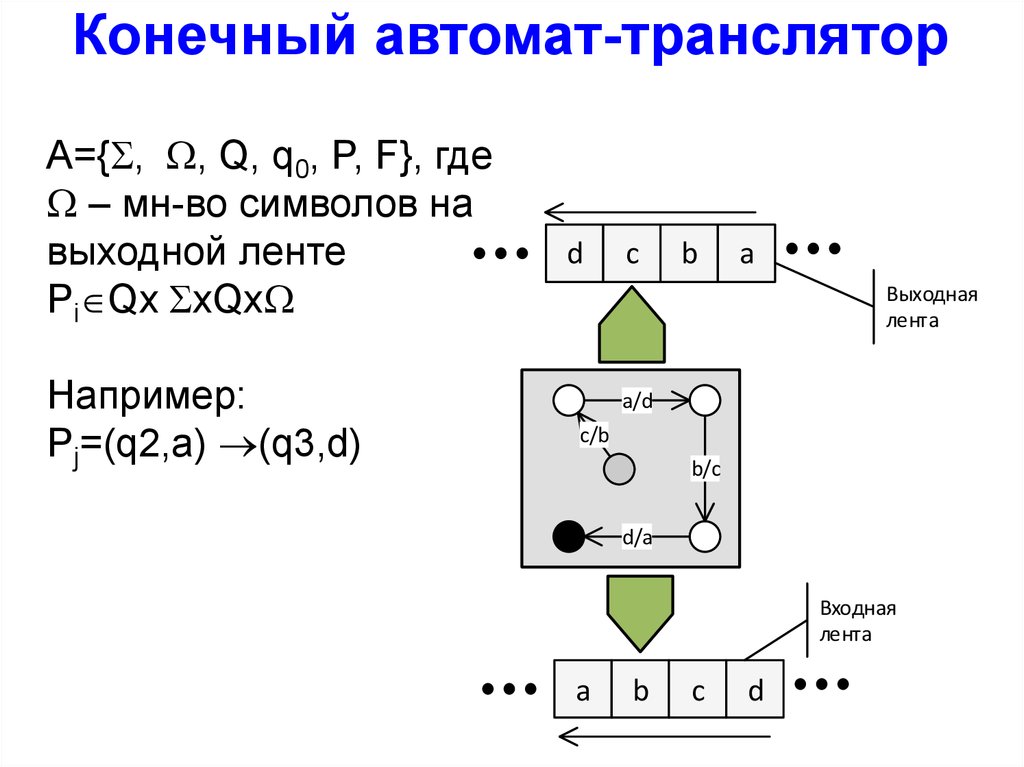
Конечный автомат-транслятор
A={ , , Q, q0, P, F}, где
– мн-во символов на
выходной ленте
Pi Qx xQx
Например:
Pj=(q2,a) (q3,d)
d
c
b
a
Выходная
лента
a/d
c/b
b/c
d/a
Входная
лента
a
b
c
d

14.

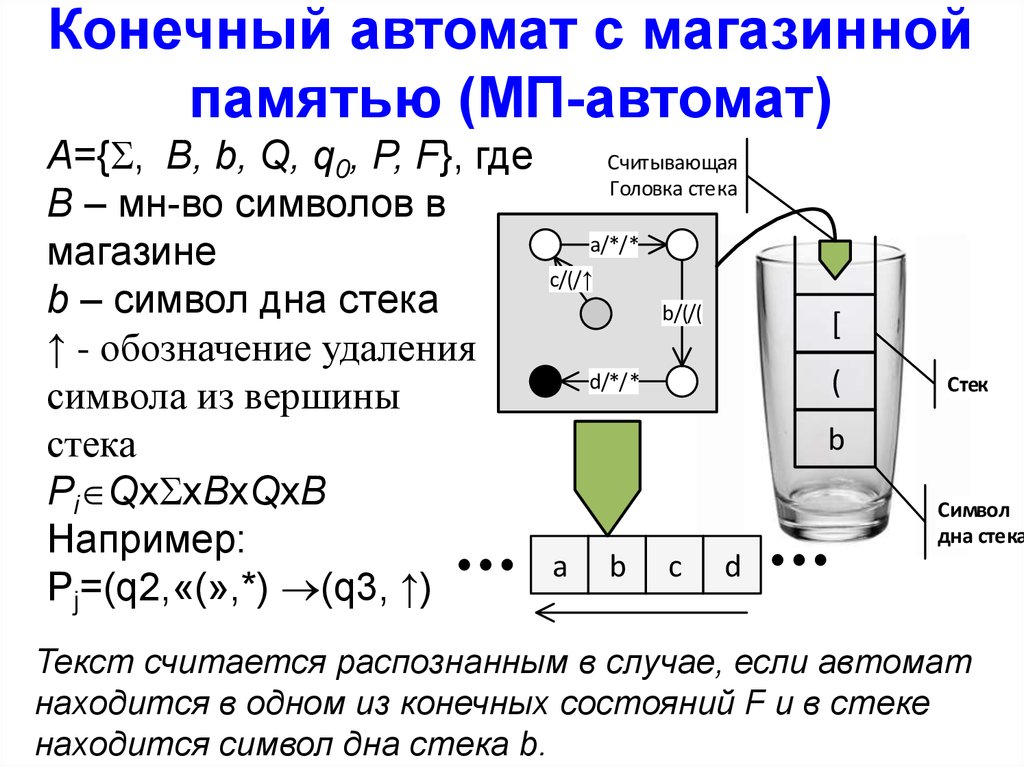
Конечный автомат с магазинной
памятью (МП-автомат)
A={ , B, b, Q, q0, P, F}, где
Считывающая
Головка стека
B – мн-во символов в
a/*/*
магазине
c/(/
b – символ дна стека
b/(/(
↑ - обозначение удаления
d/*/*
символа из вершины
стека
Pi Qx xBxQxB
Например:
a b c d
Pj=(q2,«(»,*) (q3, ↑)
[
(
Стек
b
Символ
дна стека
Текст считается распознанным в случае, если автомат
находится в одном из конечных состояний F и в стеке
находится символ дна стека b.

15.

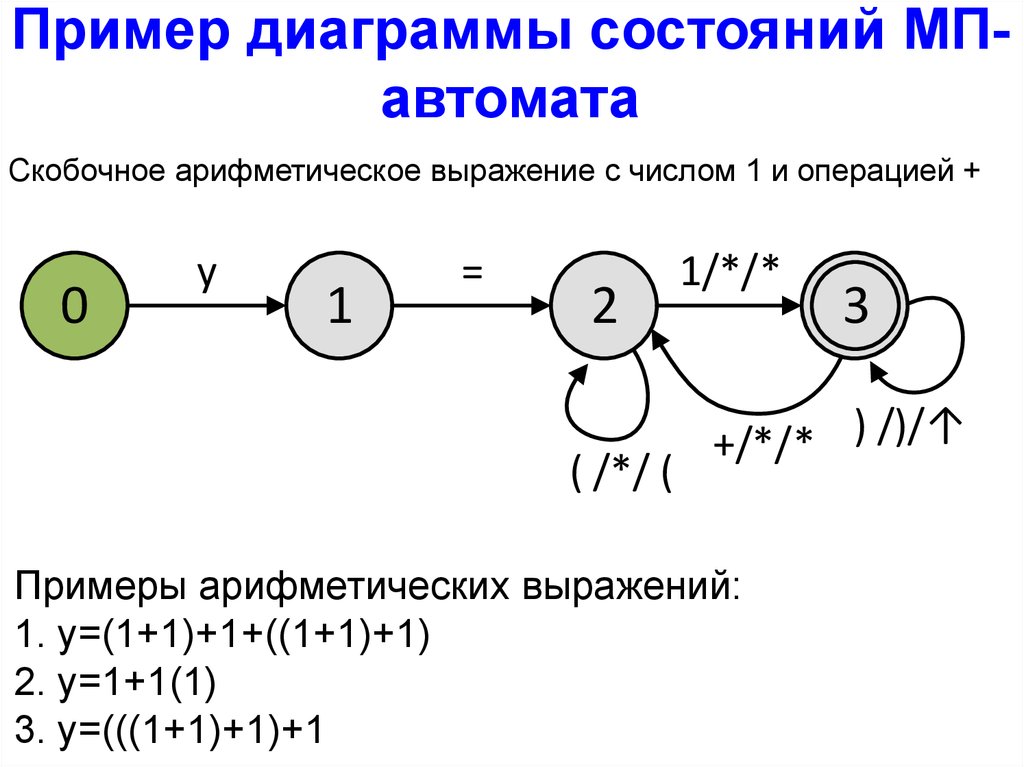
Пример диаграммы состояний МПавтомата
Скобочное арифметическое выражение с числом 1 и операцией +
0
y
1
=
2
( /*/ (
1/*/*
3
+/*/* ) /)/
Примеры арифметических выражений:
1. y=(1+1)+1+((1+1)+1)
2. y=1+1(1)
3. y=(((1+1)+1)+1

16.

Формальная грамматика
Основатель теории формальных языков – Наум Хомский (род. В 1928 г.)
Формальная грамматика предназначена для
синтеза языка
Формальная грамматика это четверка:
G={ ,N,S,P}, где
- алфавит терминальных символов;
N – алфавит нетерминальных символов;
S N – начальный символ;
P – правила вывода цепочки строк.

17.

Пример формальной грамматики (1)
Необходимо описать синтез строки, состоящей из
одинакового количества единиц и нулей, чтобы
сначала шли нули, а затем единицы, т.е. 000111
={0,1}
N={S}
S={S}
P: 1. S 0S1
2. S 01

18.

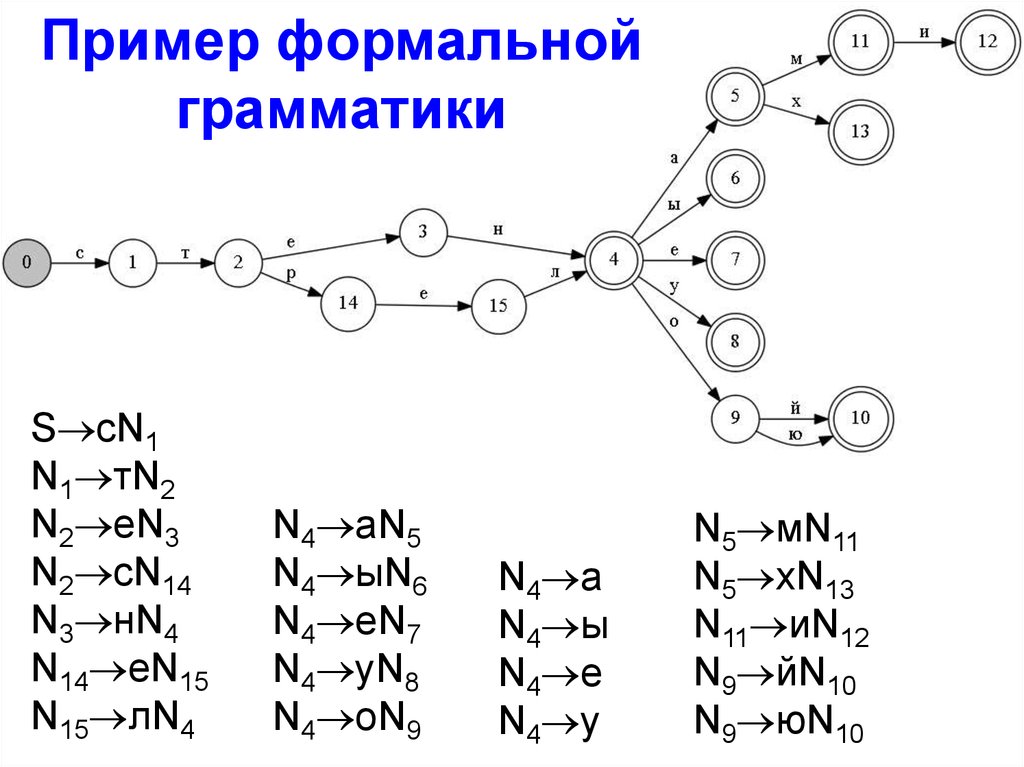
Пример формальной
грамматики
S сN1
N1 тN2
N2 еN3
N2 сN14
N3 нN4
N14 еN15
N15 лN4
N4 аN5
N4 ыN6
N4 еN7
N4 уN8
N4 оN9
N4 а
N4 ы
N4 е
N4 у
N5 мN11
N5 хN13
N11 иN12
N9 йN10
N9 юN10

19.

Другие виды записи формальных
грамматик
- Форма Бекуса-Наура (БНФ)
- Расширенная форма Бекуса-Наура (РБНФ)
- Регулярные выражения

20.

Иерархия формальных языков
Н. Хомского
Четыре класса языков:
0: Свободные - нет ограничений на правила.
1: Контекстно-зависимые - правила вида , где ,
, , - строки из терминалов и нетерминалов
2: Контекстно-свободные - A , где A – символнетерминал, - строка из терминалов и нетерминалов
3: автоматные (регулярные) - N aA или N Aa, где A –
нетерминальный символ, a – терминальный символ.

21.

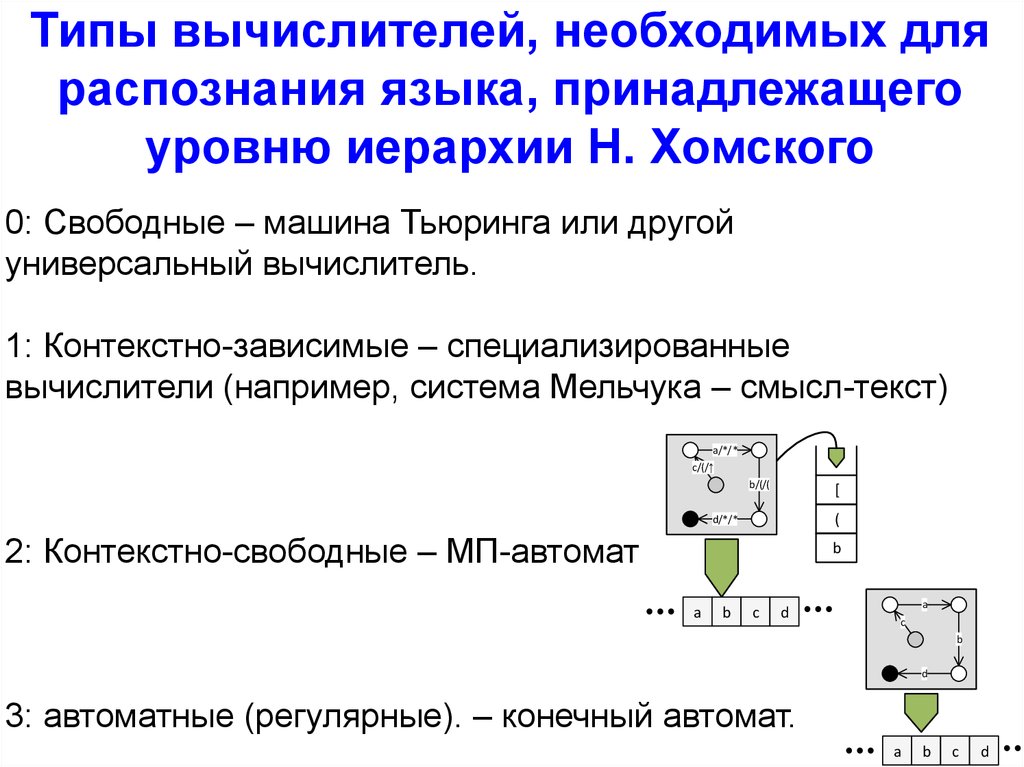
Типы вычислителей, необходимых для
распознания языка, принадлежащего
уровню иерархии Н. Хомского
0: Свободные – машина Тьюринга или другой
универсальный вычислитель.
1: Контекстно-зависимые – специализированные
вычислители (например, система Мельчука – смысл-текст)
a/*/*
c/(/
b/(/(
[
(
d/*/*
2: Контекстно-свободные – МП-автомат
b
a
b
c
d
a
c
b
d
3: автоматные (регулярные). – конечный автомат.
a
b
c
d

22.

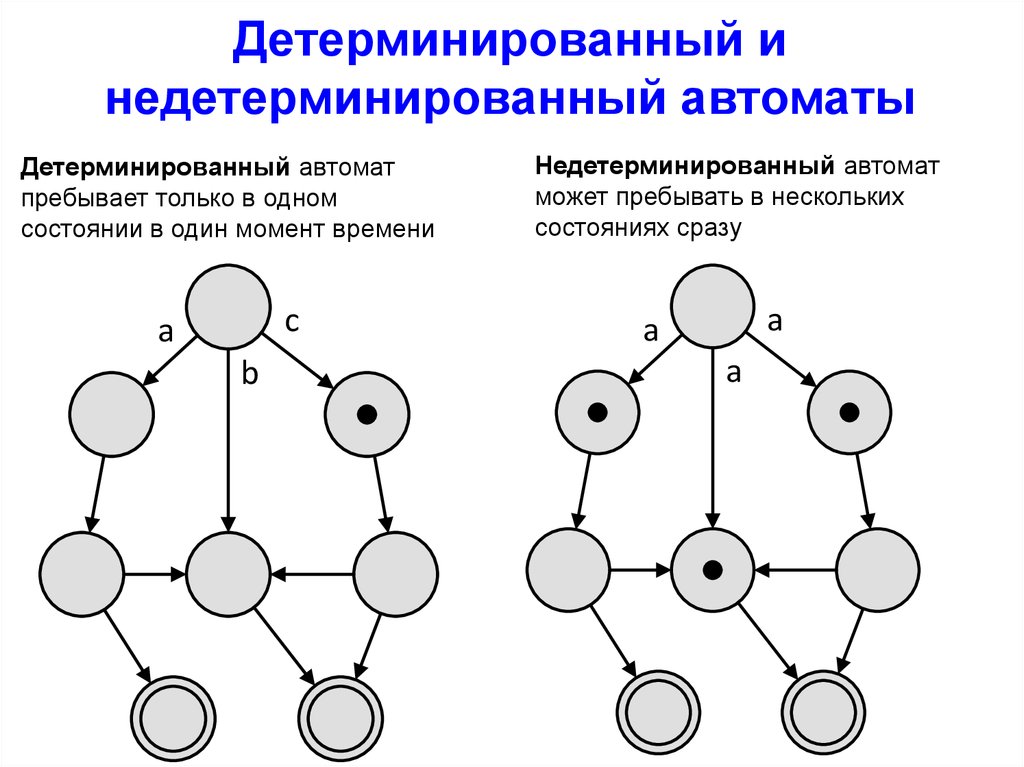
Детерминированный и
недетерминированный автоматы
Детерминированный автомат
пребывает только в одном
состоянии в один момент времени
c
a
b
Недетерминированный автомат
может пребывать в нескольких
состояниях сразу
a
a
a

23.

Алгоритм получения ДА из НДА
1. Сформировать начальное состояние ДА и приписать ему метки
начального(-ых) состояние(-ия) НДА.
2. Выделить все символы, по которым происходит переход из
начального(ых) состояния(-ий) НДА – из начального состояния ДА
вывести дуги (переходы), помеченные выделенными символами. С
концом каждой дуги сопоставить состояние и пометить его метками
состояния НДА, в которые происходит переход из начального состояния
(-ий) по символу, приписанному к дуге ДА.
3. Для каждой сформированной вершины ДА выделить символы, по
которым из вершин НДА, метки которых имеются в состоянии ДА,
каждому символу сопоставить дугу, выходящую из узла ДА. Концу
каждой дуги сопоставить состояние ДА, с метками вершин НДА, куда
выходят дуги с меткой дуги ДА.
4. И т.д.
5. После того, как не удается сформировать в ДА состояний с новыми
метками, выделяем в ДА конечные состояния: конечным является
состояние, в метке которого присутствует хотя бы одна метка конечного
состояния НДА.

24.

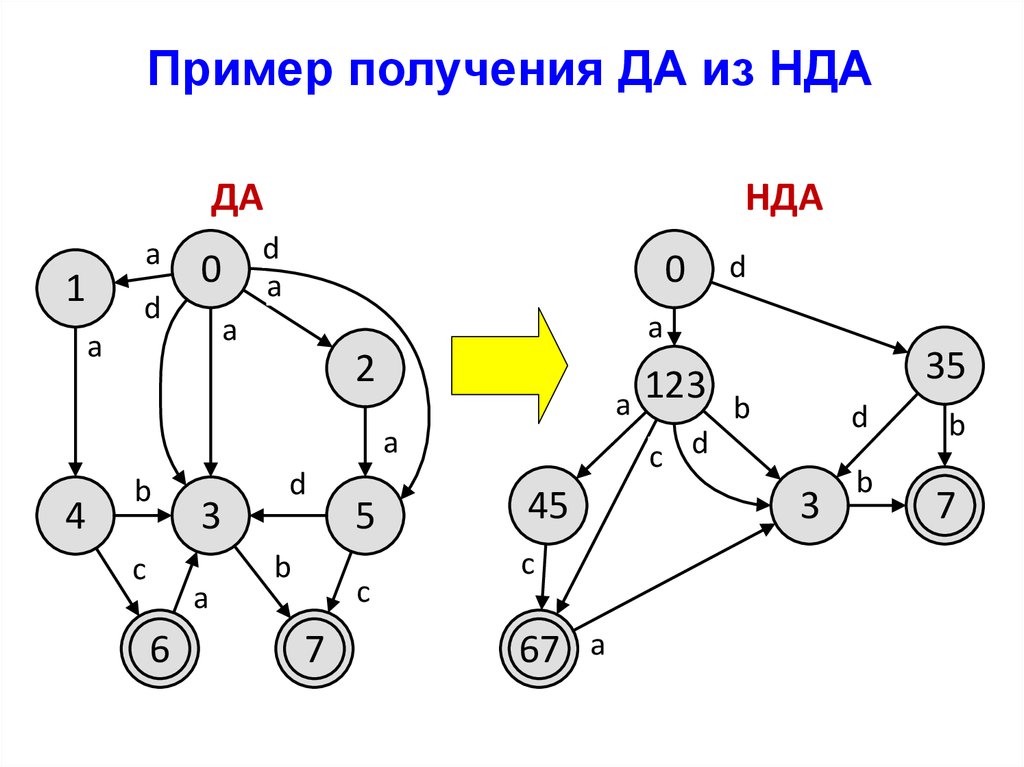
25.

Пример получения ДА из НДА
ДА
a
1
d
a
0
d
НДА
0
a
a
a
2
a
a
4
b
c
3
a
6
d
d
b
5
c
7
123
35
b
d
c d
45
3
c
67
a
b
b
7

26.

Программная реализация ДА
1. Объявить переменную, хранящую номер состояния ДА
(например, S).
2. Объявить переменную, хранящую текущий
распознаваемый символ (например, ch).
3. Создать цикл и в нем языковую конструкцию
множественного выбора (switch) относительно
переменной, хранящей текущий распознаваемый символ.
Каждый вариант множественного выбора соответствует
состоянию ДА.
4. В каждой альтернативе множественного выбора
произвести анализ текущего символа и относительно
него произвести изменение состояния ДА S. Если
текущий символ последний, то проверить, находится для
ДА в конечном состоянии.

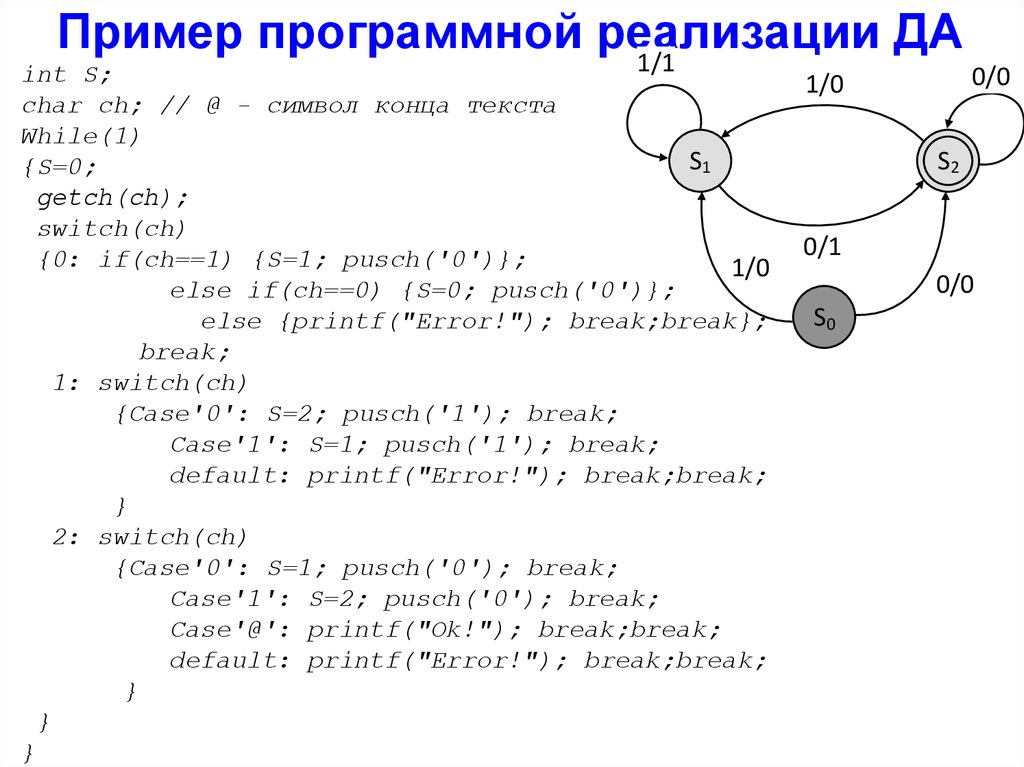
27.

Пример программной реализации
ДА
1/1
int S;
char ch; // @ - символ конца текста
While(1)
S1
{S=0;
getch(ch);
switch(ch)
{0: if(ch==1) {S=1; pusch('0')};
1/0
else if(ch==0) {S=0; pusch('0')};
else {printf("Error!"); break;break};
break;
1: switch(ch)
{Case'0': S=2; pusch('1'); break;
Case'1': S=1; pusch('1'); break;
default: printf("Error!"); break;break;
}
2: switch(ch)
{Case'0': S=1; pusch('0'); break;
Case'1': S=2; pusch('0'); break;
Case'@': printf("Ok!"); break;break;
default: printf("Error!"); break;break;
}
}
}
1/0
0/0
S2
0/1
0/0
S0

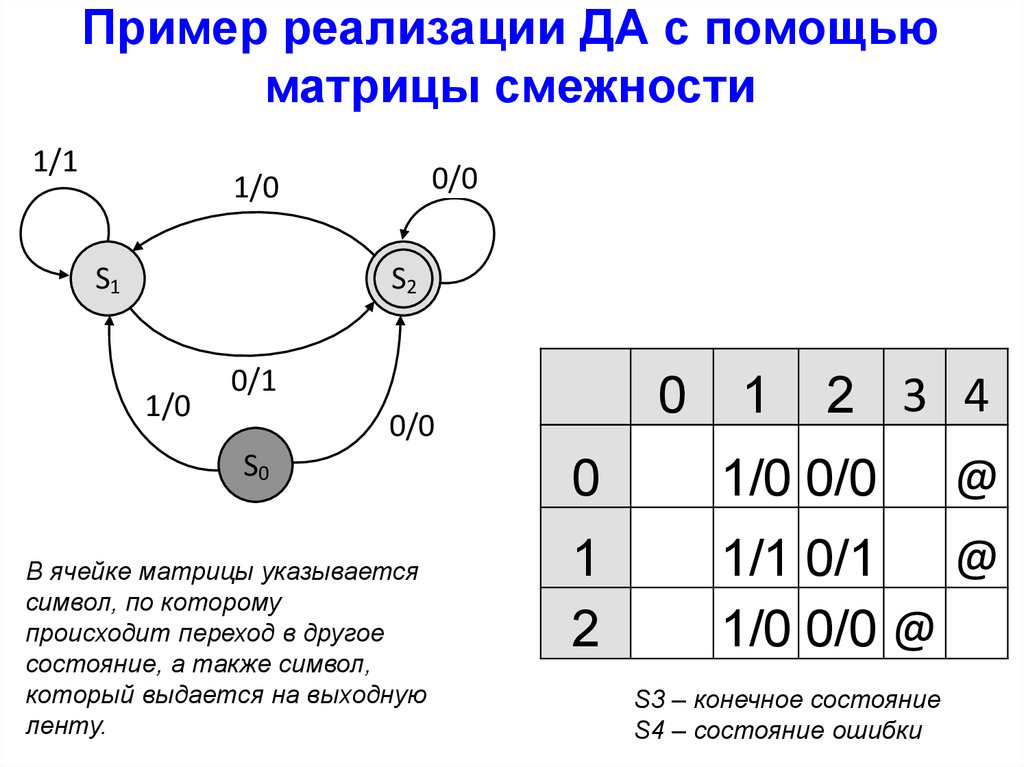
28.

Пример реализации ДА с помощью
матрицы смежности
1/1
0/0
1/0
S1
S2
1/0
0/1
0
0/0
S0
В ячейке матрицы указывается
символ, по которому
происходит переход в другое
состояние, а также символ,
который выдается на выходную
ленту.
1
2 3 4
@
0
1/0 0/0
1
2
1/1 0/1 @
1/0 0/0 @
S3 – конечное состояние
S4 – состояние ошибки

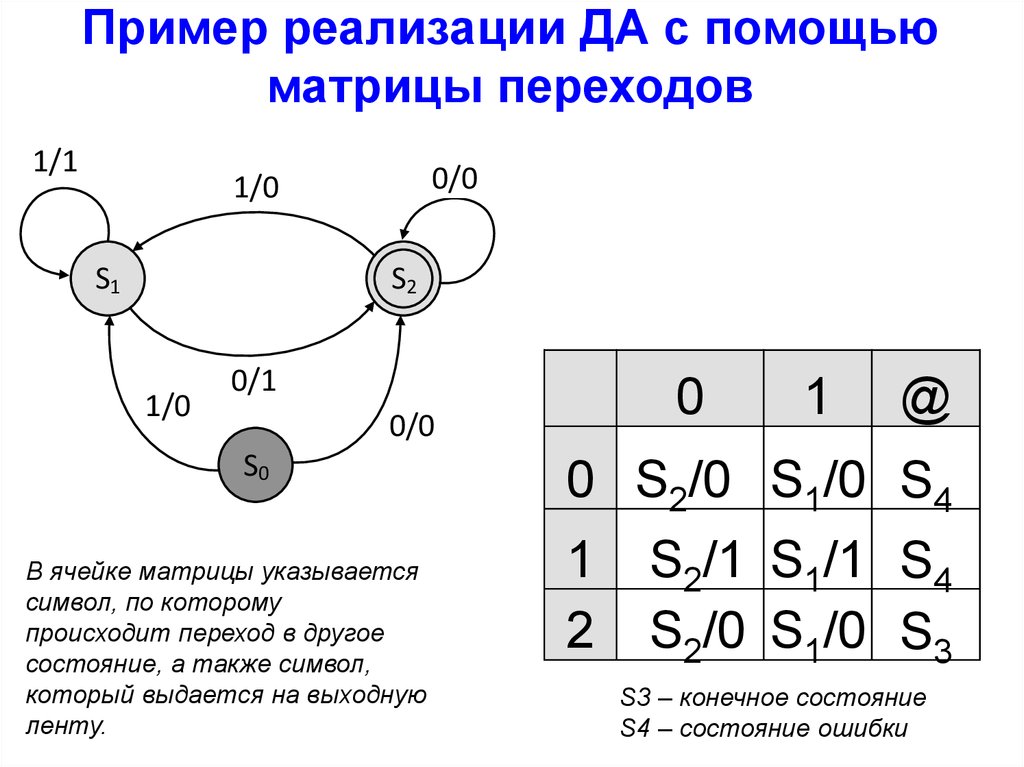
29.

Пример реализации ДА с помощью
матрицы переходов
1/1
0/0
1/0
S1
S2
1/0
0/1
0
0/0
S0
В ячейке матрицы указывается
символ, по которому
происходит переход в другое
состояние, а также символ,
который выдается на выходную
ленту.
1
@
0 S2/0 S1/0 S4
1
2
S2/1 S1/1 S4
S2/0 S1/0 S3
S3 – конечное состояние
S4 – состояние ошибки

30.

Реализация НДА
Реализация НДА намного сложнее, чем ДА:
необходимо вводить не одну переменную, хранящую
состояние автомата (S), а вектор множество
состояний. Поэтому разработчики программ и
аппаратуры и стараются свести НДА к ДА!

31.

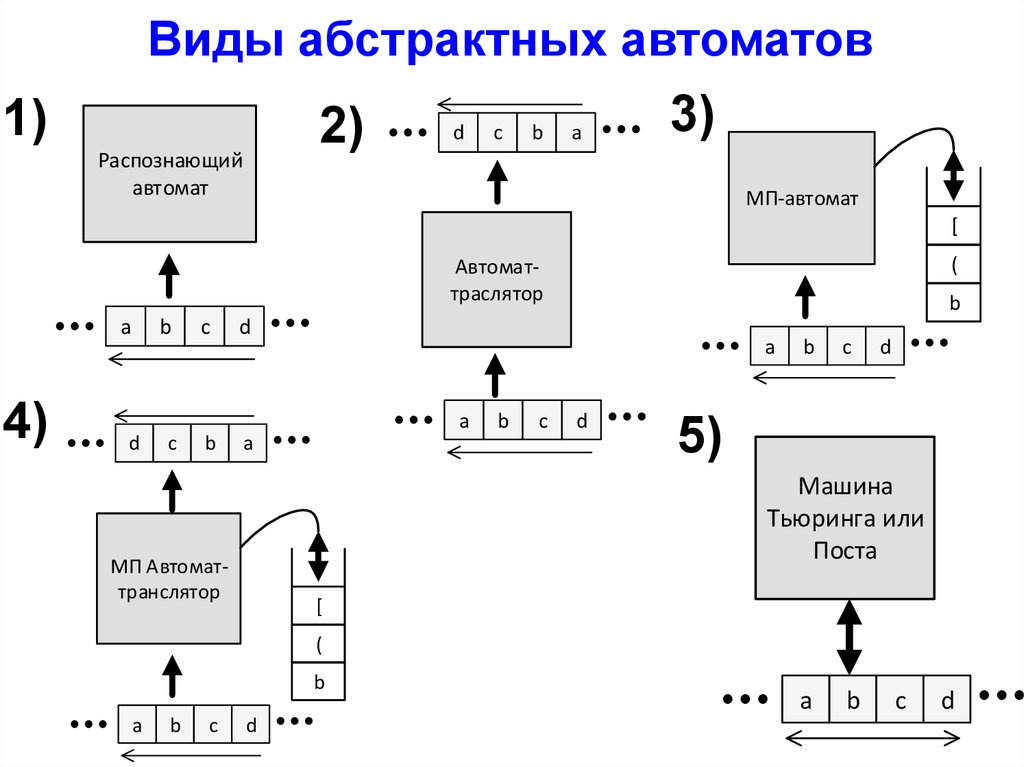
Виды абстрактных автоматов
1. Распознающий автомат (лента движется в одну
сторону, символы на ленте не изменяются
2. Автомат-транслятор – две ленты, движущиеся в одном
направлении.
3. Автомат с магазинной памятью (МП-автомат) входная лента движется в одном направлении и
только читается. Вторая лента выступает в роли стека
(запись и чтение осуществляется только в верхушки
стека.
4. МП автомат-транслятор – считывает символы со
входной ленты, записывает на выходную ленту,
промежуточные данные записывает в стек
5. Машина Тьюринга и машина Поста – автомат может
двигать ленту в обоих направлениях и может изменять
символы на ленте

32.

Виды абстрактных автоматов
1)
2)
Распознающий
автомат
d
c
b
a
3)
МП-автомат
[
(
Автоматтраслятор
a
4)
b
c
d
a
a
d
c
b
b
a
b
c
d
b
c
d
5)
Машина
Тьюринга или
Поста
МП Автоматтранслятор
[
(
b
a
b
c
d
a
b
c
d

33.

Об информации на входной ленте
абстрактного автомата
Входная лента автомат может содержать не только
символы, но и другие информационные конструкции!!!
Например, в теории компиляции имеется такие понятия как
лексический и синтаксический автоматы. Лексический
занимается выделением из цепочки символов лексем
(слова, числа, разделительные знаки) и формирование их
описания в виде токенов. Токен описывает лексему и
состоит из двух частей: атрибута, описывающего тип
лексемы, и самой лексемы. Типы лексем могут быть:
константа, переменная, зарезервированное слово,
разделительный знак. Синтаксический автомат принимает
на вход токены и обрабатывает их. Т.е. на входной ленте
синтаксического автомата находятся не символы, а
токены!!!

34.

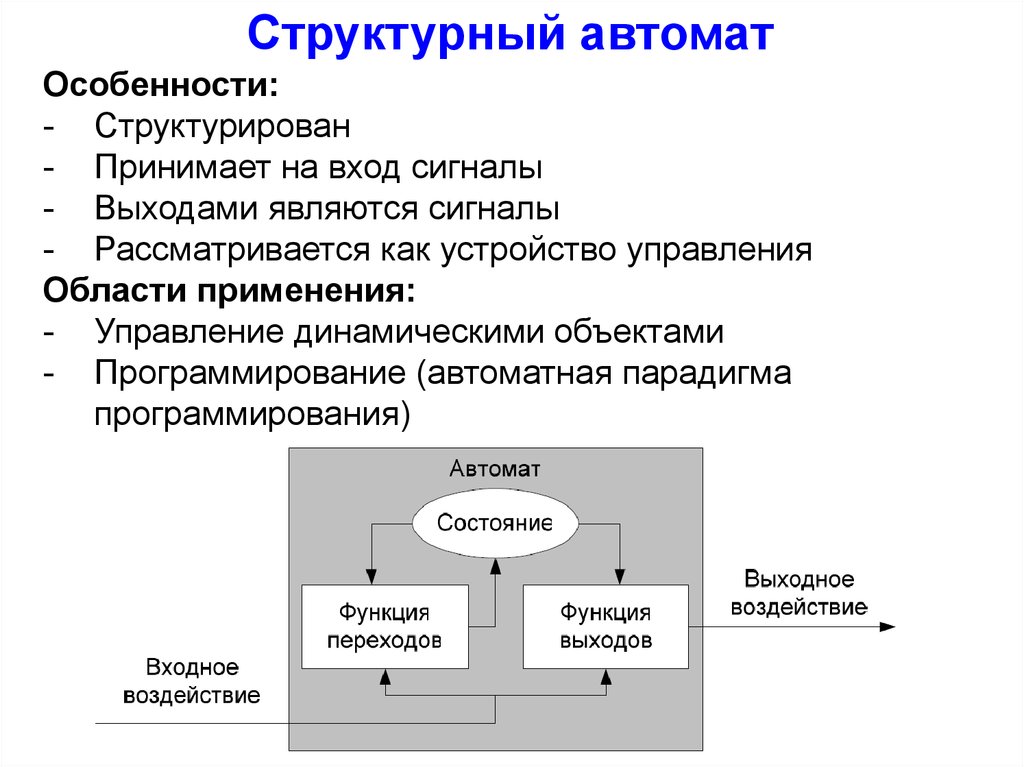
Структурный автомат
Особенности:
- Структурирован
- Принимает на вход сигналы
- Выходами являются сигналы
- Рассматривается как устройство управления
Области применения:
- Управление динамическими объектами
- Программирование (автоматная парадигма
программирования)

35.

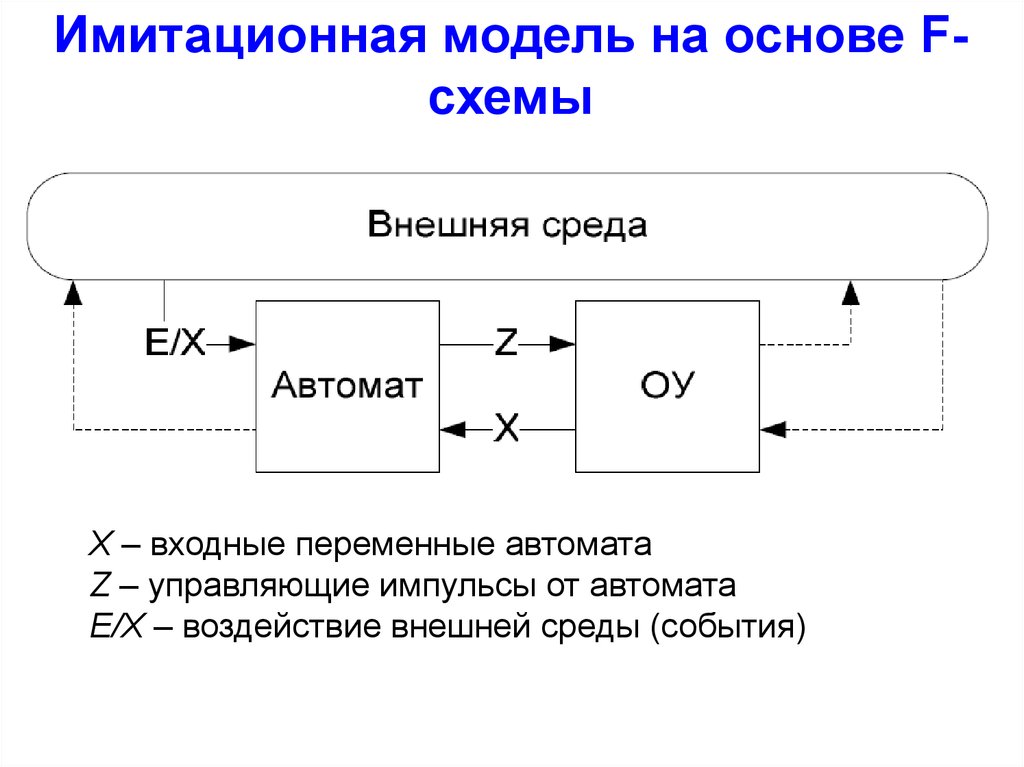
Имитационная модель на основе Fсхемы
X – входные переменные автомата
Z – управляющие импульсы от автомата
E/X – воздействие внешней среды (события)

36.

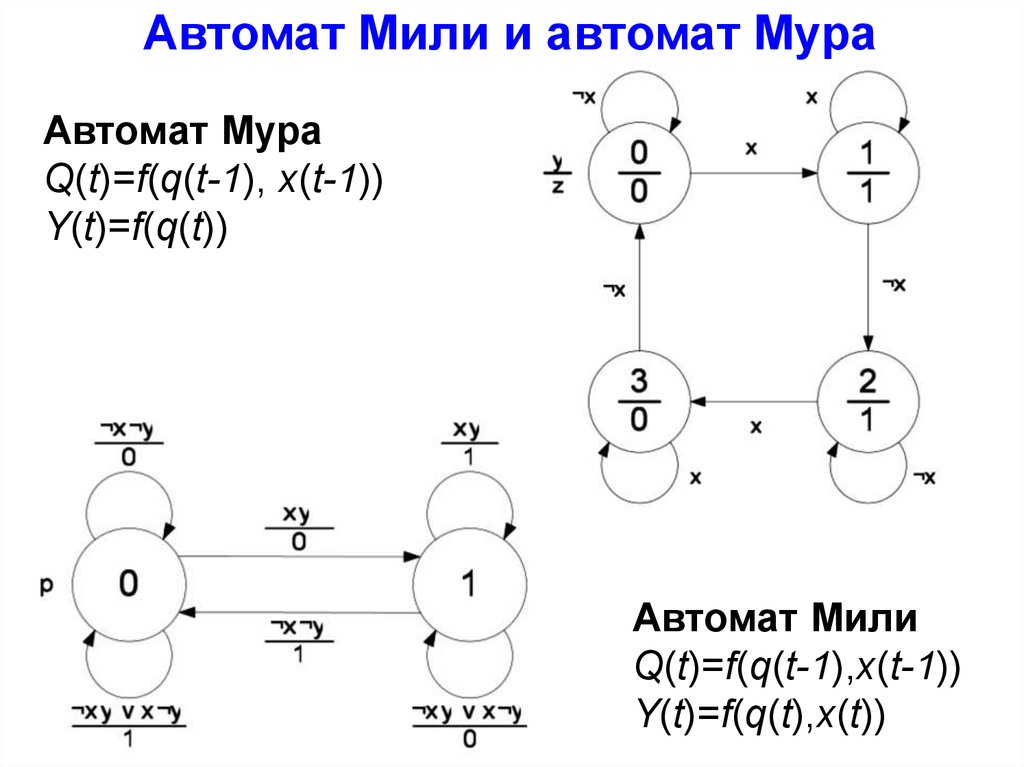
Автомат Мили и автомат Мура
Автомат Мура
Q(t)=f(q(t-1), x(t-1))
Y(t)=f(q(t))
Автомат Мили
Q(t)=f(q(t-1),x(t-1))
Y(t)=f(q(t),x(t))

37.

Автоматизированный объект управления
Управляющий автомат – это шестерка {X,Y,Z, y0, , }, где
X=XE x XO – сигналы от внешней среды и объекта управления.
Y – множество состояний автомата.
Z – множество выходных воздействий.
Y0 – начальное состояние
=( ', ‘') – функция переходов: ‘: Y Z функции в состояниях, ‘‘: XxY Z
функции в на переходах
: XxZ Y

38.

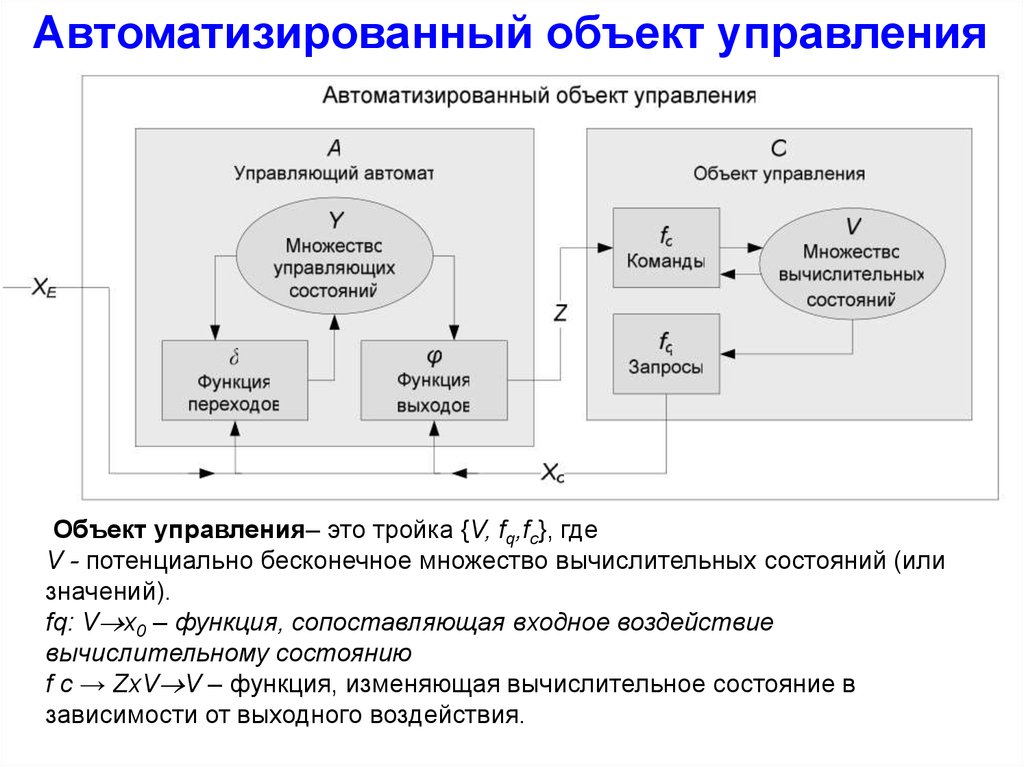
Автоматизированный объект управления
Объект управления– это тройка {V, fq,fc}, где
V - потенциально бесконечное множество вычислительных состояний (или
значений).
fq: V x0 – функция, сопоставляющая входное воздействие
вычислительному состоянию
f c → ZxV V – функция, изменяющая вычислительное состояние в
зависимости от выходного воздействия.

39.

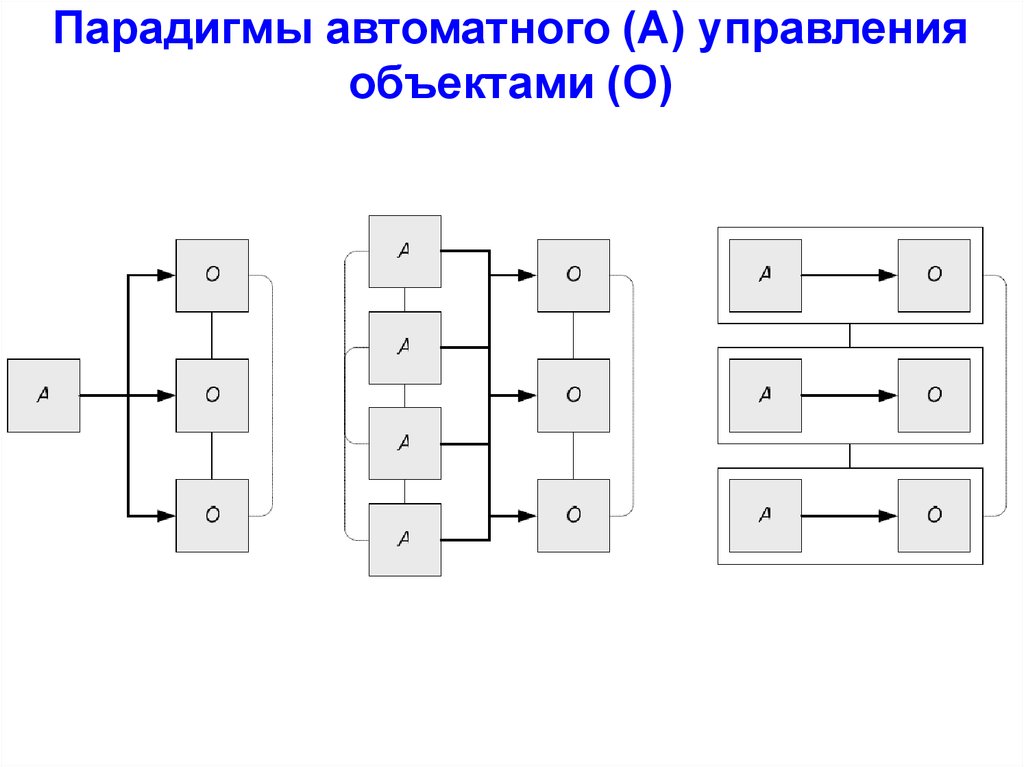
Парадигмы автоматного (А) управления
объектами (О)

40.

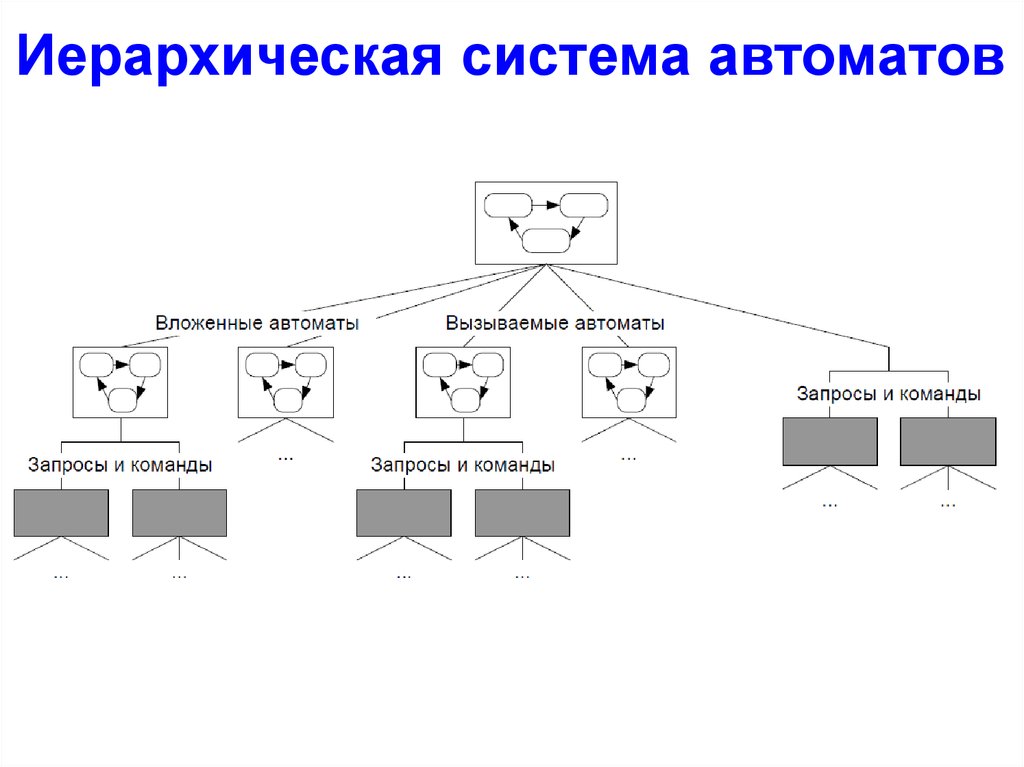
Иерархическая система автоматов

41.

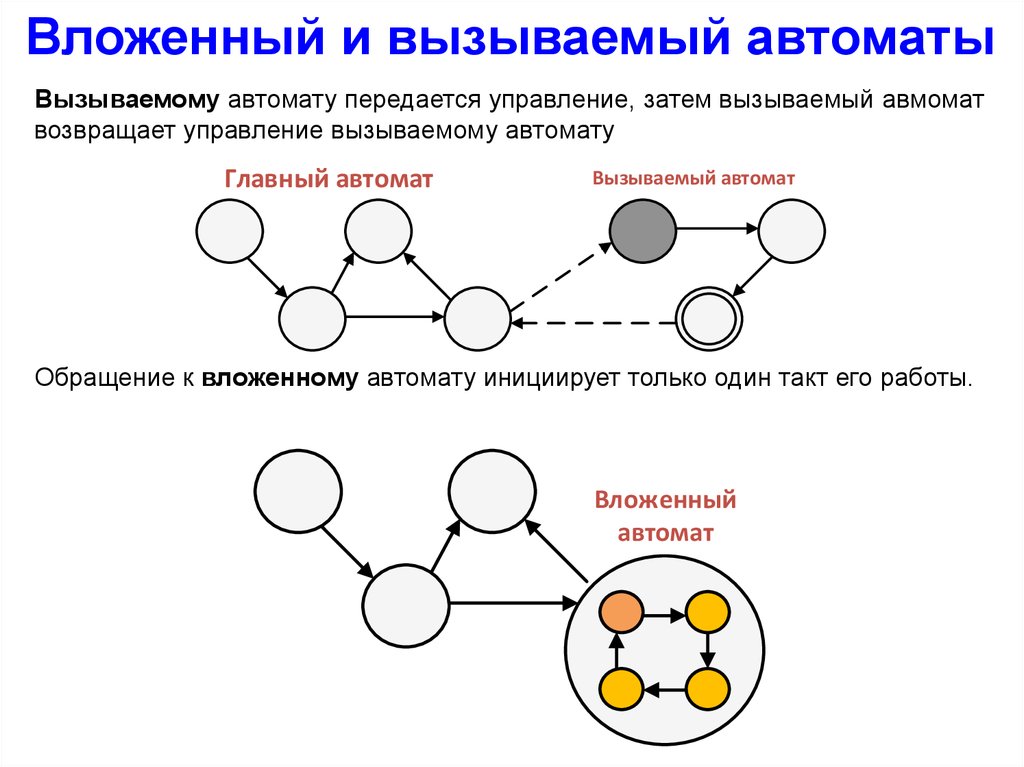
Вложенный и вызываемый автоматы
Вызываемому автомату передается управление, затем вызываемый авмомат
возвращает управление вызываемому автомату
Главный автомат
Вызываемый автомат
Обращение к вложенному автомату инициирует только один такт его работы.
Вложенный
автомат

42.

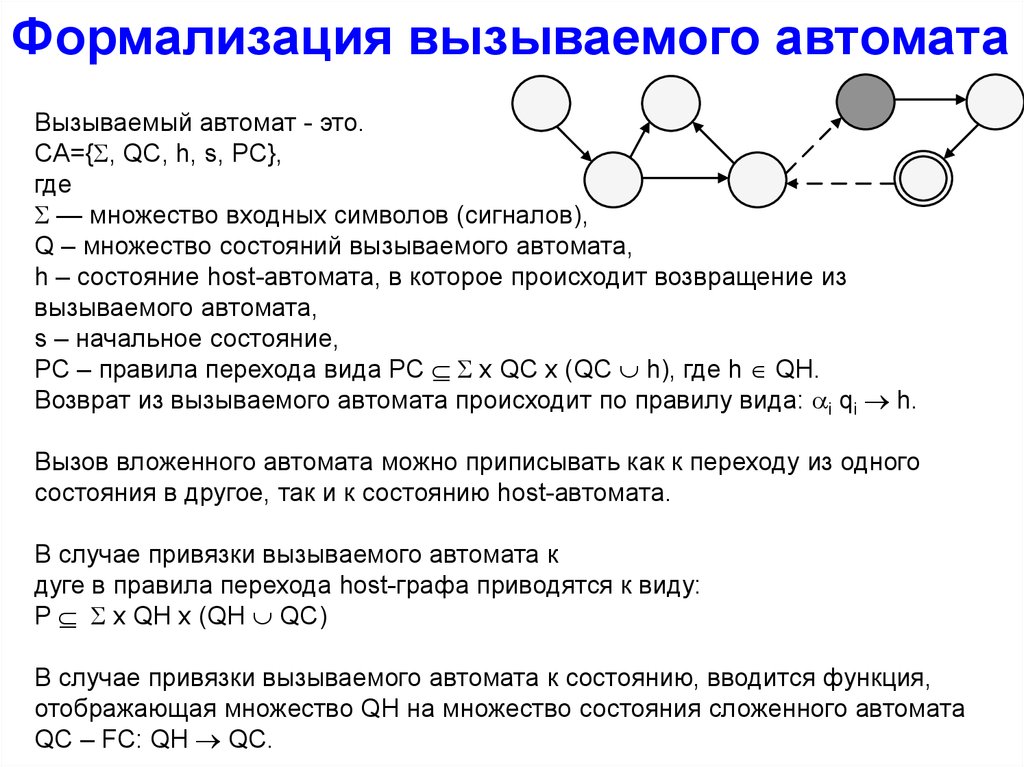
Формализация вызываемого автомата
Вызываемый автомат - это.
CA={ , QC, h, s, PC},
где
— множество входных символов (сигналов),
Q – множество состояний вызываемого автомата,
h – состояние host-автомата, в которое происходит возвращение из
вызываемого автомата,
s – начальное состояние,
PС – правила перехода вида PС x QС x (QС h), где h QH.
Возврат из вызываемого автомата происходит по правилу вида: i qi h.
Вызов вложенного автомата можно приписывать как к переходу из одного
состояния в другое, так и к состоянию host-автомата.
В случае привязки вызываемого автомата к
дуге в правила перехода host-графа приводятся к виду:
P x QH x (QH QC)
В случае привязки вызываемого автомата к состоянию, вводится функция,
отображающая множество QH на множество состояния сложенного автомата
QC – FC: QH QC.

43.

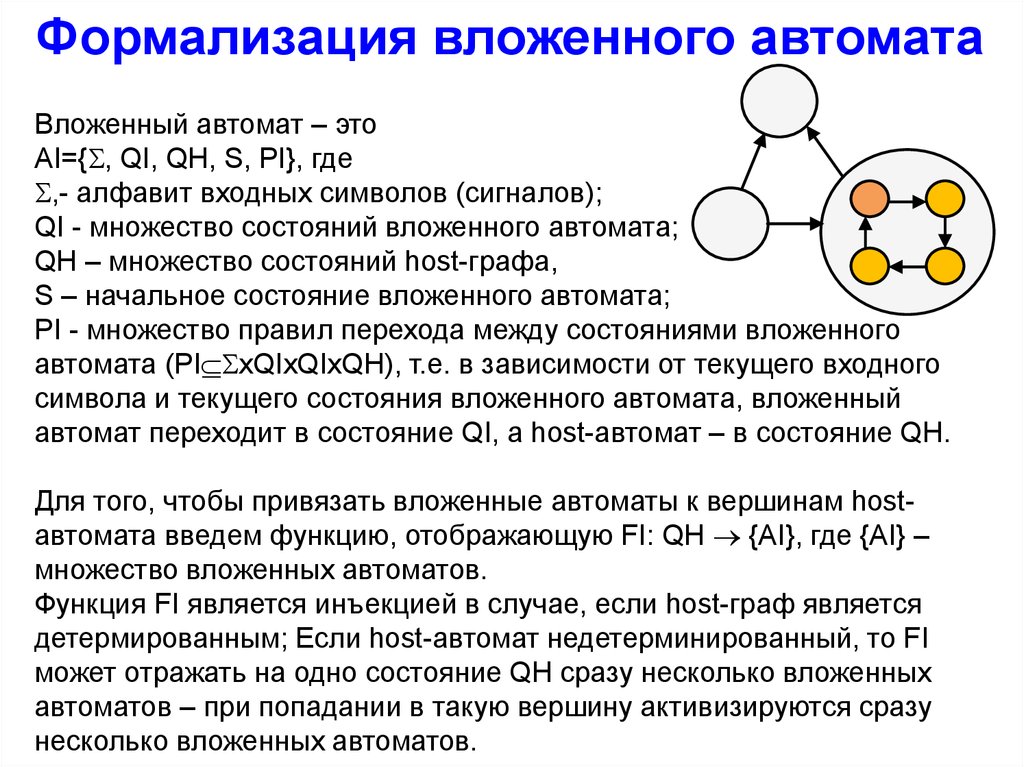
Формализация вложенного автомата
Вложенный автомат – это
AI={ , QI, QH, S, PI}, где
,- алфавит входных символов (сигналов);
QI - множество состояний вложенного автомата;
QH – множество состояний host-графа,
S – начальное состояние вложенного автомата;
PI - множество правил перехода между состояниями вложенного
автомата (PI xQIxQIxQH), т.е. в зависимости от текущего входного
символа и текущего состояния вложенного автомата, вложенный
автомат переходит в состояние QI, а host-автомат – в состояние QH.
Для того, чтобы привязать вложенные автоматы к вершинам hostавтомата введем функцию, отображающую FI: QH {AI}, где {AI} –
множество вложенных автоматов.
Функция FI является инъекцией в случае, если host-граф является
детермированным; Если host-автомат недетерминированный, то FI
может отражать на одно состояние QH сразу несколько вложенных
автоматов – при попадании в такую вершину активизируются сразу
несколько вложенных автоматов.

44.

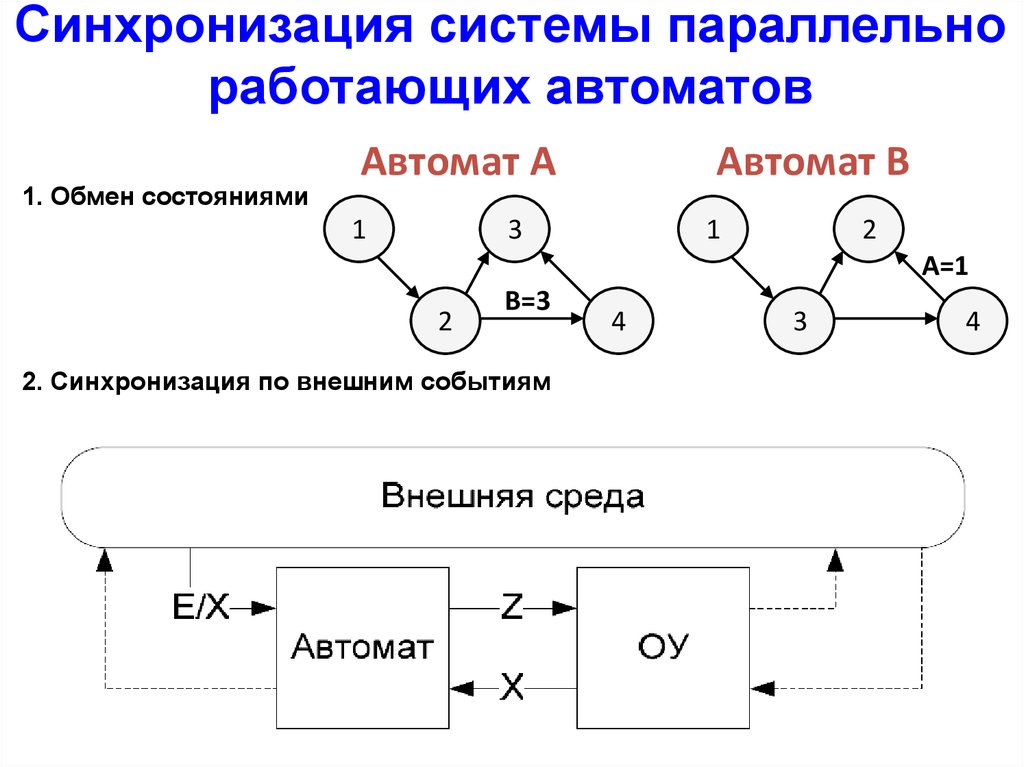
Синхронизация системы параллельно
работающих автоматов
1. Обмен состояниями
Автомат А
1
Автомат B
3
1
2
A=1
2
B=3
2. Синхронизация по внешним событиям
4
3
4

45.

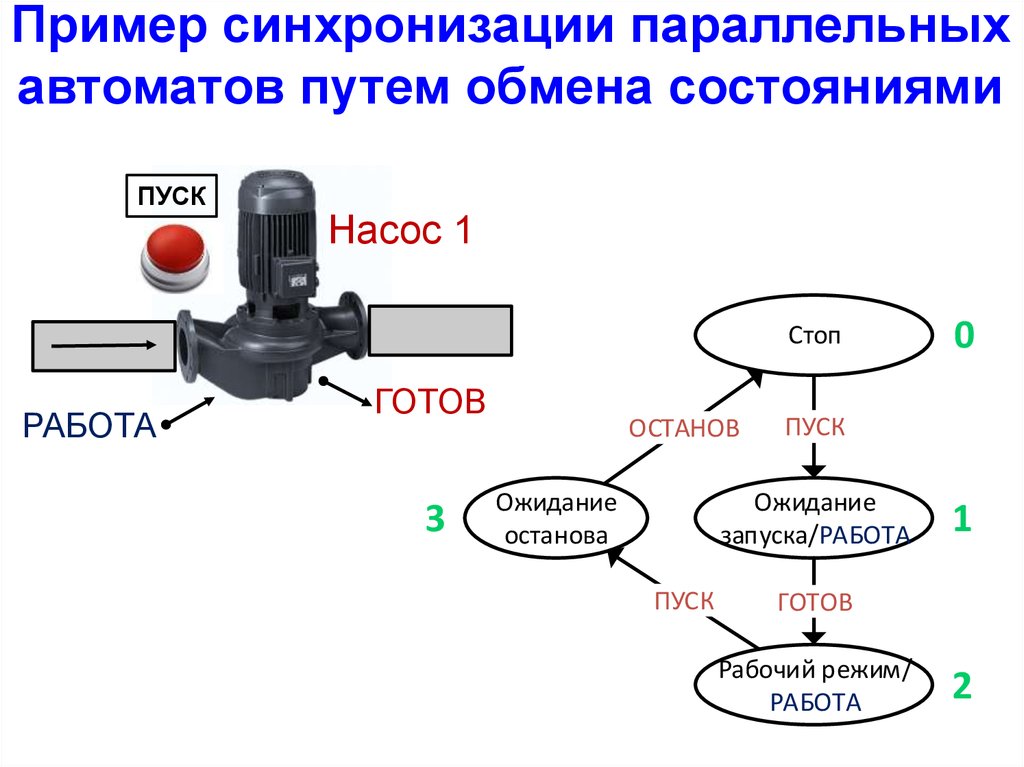
Пример синхронизации параллельных
автоматов путем обмена состояниями
ПУСК
Насос 1
Стоп
РАБОТА
ГОТОВ
3
ОСТАНОВ
Ожидание
останова
ПУСК
Ожидание
запуска/РАБОТА
ПУСК
0
1
ГОТОВ
Рабочий режим/
РАБОТА
2

46.

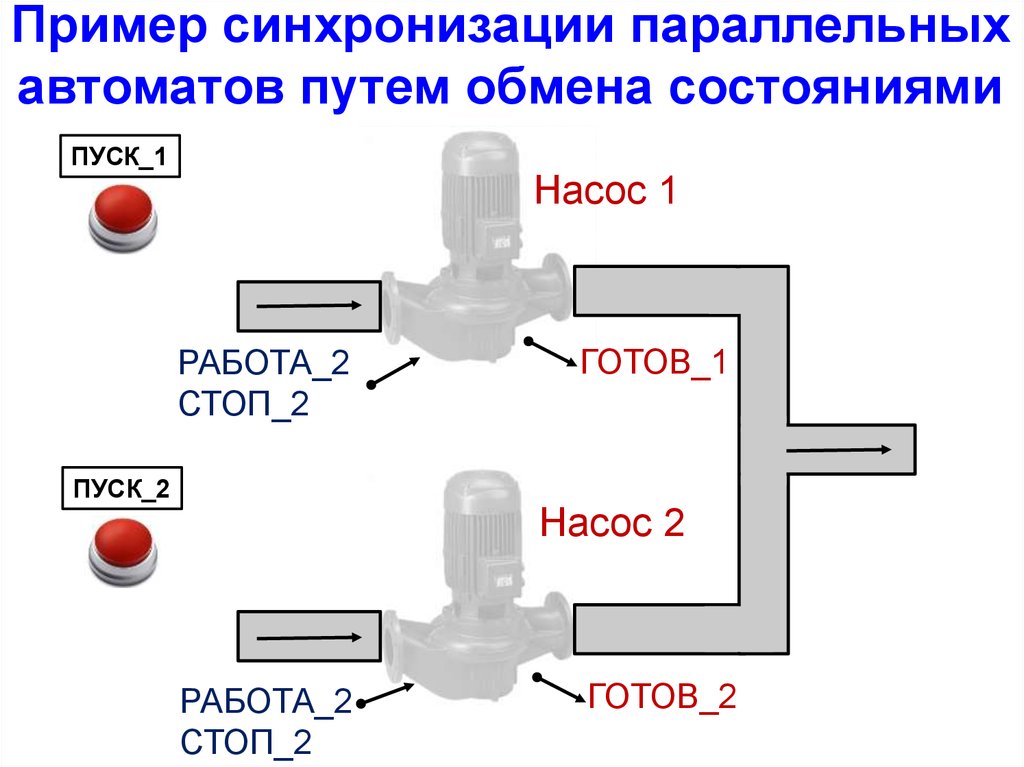
Пример синхронизации параллельных
автоматов путем обмена состояниями
ПУСК_1
Насос 1
РАБОТА_2
СТОП_2
ПУСК_2
ГОТОВ_1
Насос 2
РАБОТА_2
СТОП_2
ГОТОВ_2

47.

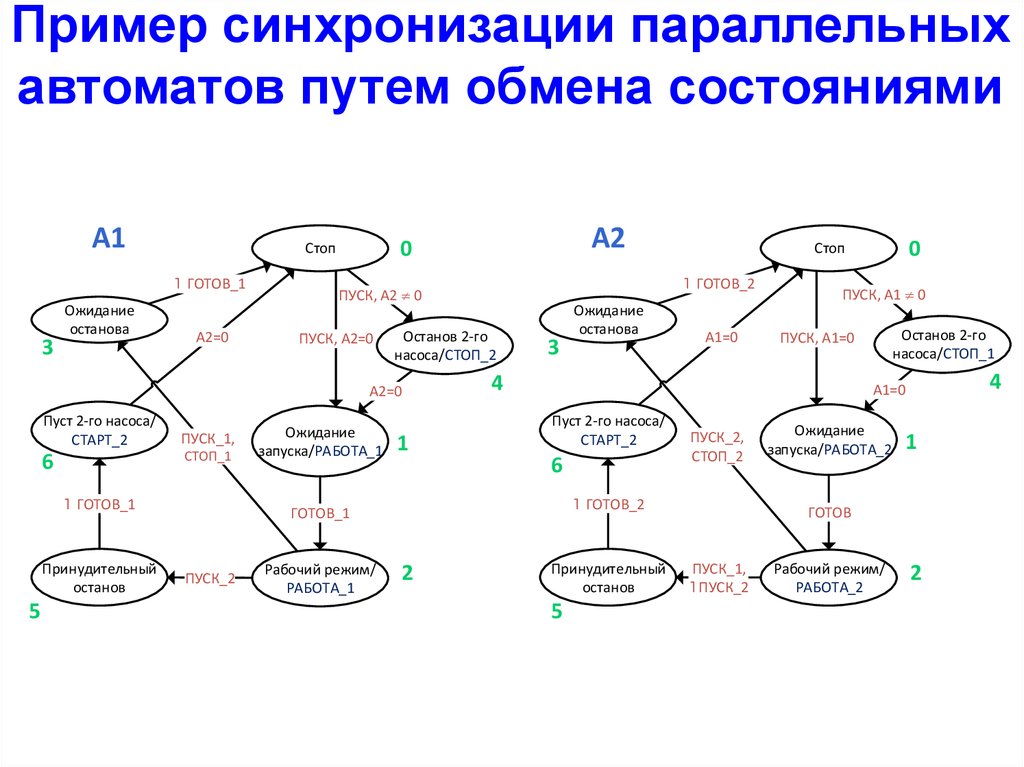
Пример синхронизации параллельных
автоматов путем обмена состояниями
A1
˥ ГОТОВ_1
3
Ожидание
останова
A2=0
ПУСК, A2=0
Останов 2-го
насоса/СТОП_2
ПУСК_1,
СТОП_1
6
˥ ГОТОВ_1
Принудительный
останов
5
Ожидание
запуска/РАБОТА_1
1
3
Рабочий режим/
РАБОТА_1
A1=0
Останов 2-го
насоса/СТОП_1
ПУСК, A1=0
4
A1=0
Пуст 2-го насоса/
СТАРТ_2
6
ПУСК_2,
СТОП_2
˥ ГОТОВ_2
2
ПУСК, A1 0
4
ГОТОВ_1
ПУСК_2
Ожидание
останова
0
Стоп
˥ ГОТОВ_2
ПУСК, A2 0
A2=0
Пуст 2-го насоса/
СТАРТ_2
A2
0
Стоп
Принудительный
останов
5
Ожидание
запуска/РАБОТА_2
1
ГОТОВ
ПУСК_1,
˥ ПУСК_2
Рабочий режим/
РАБОТА_2
2

48.

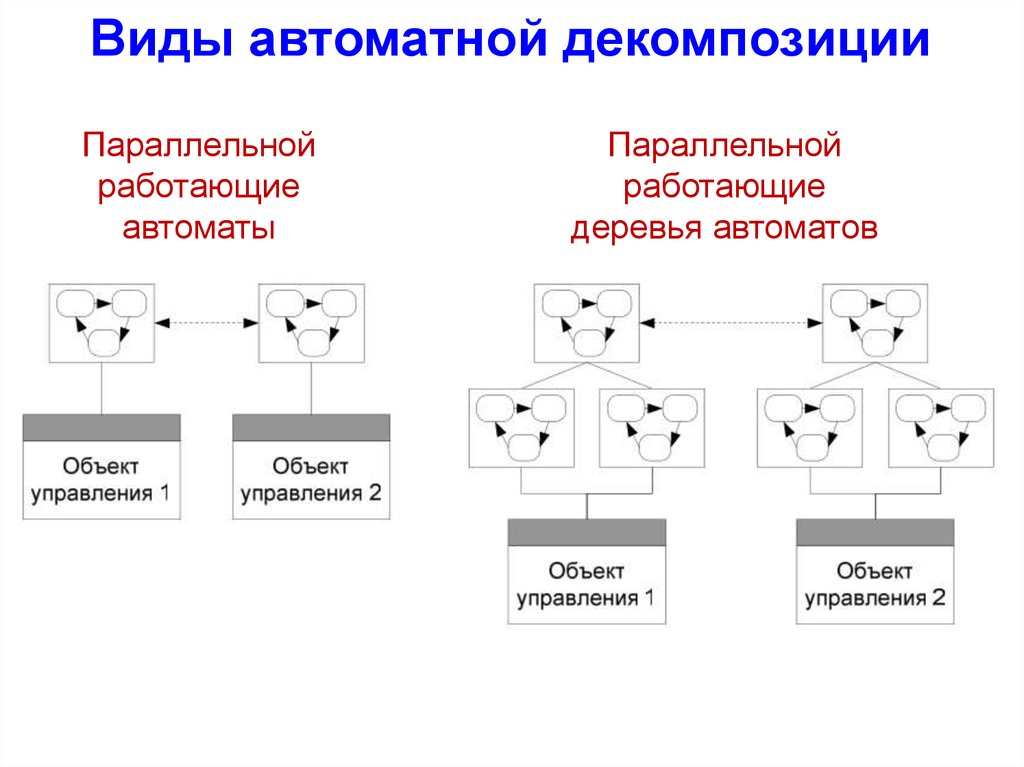
Виды автоматной декомпозиции
Параллельной
работающие
автоматы
Параллельной
работающие
деревья автоматов

49.

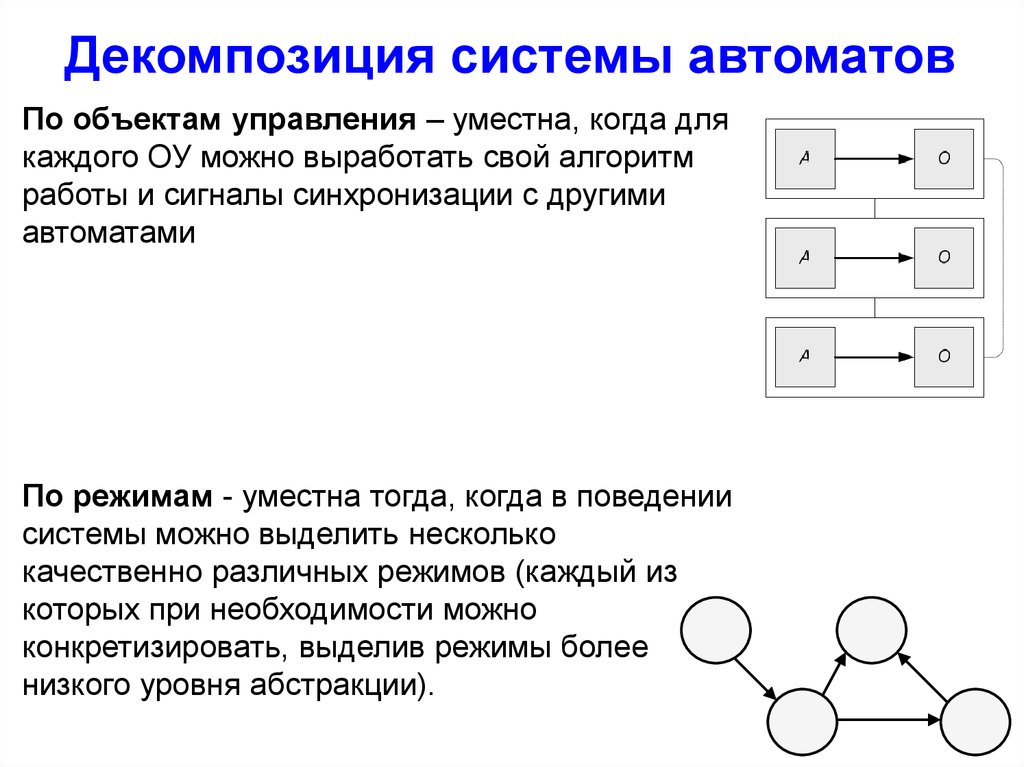
Декомпозиция системы автоматов
По объектам управления – уместна, когда для
каждого ОУ можно выработать свой алгоритм
работы и сигналы синхронизации с другими
автоматами
По режимам - уместна тогда, когда в поведении
системы можно выделить несколько
качественно различных режимов (каждый из
которых при необходимости можно
конкретизировать, выделив режимы более
низкого уровня абстракции).

50.

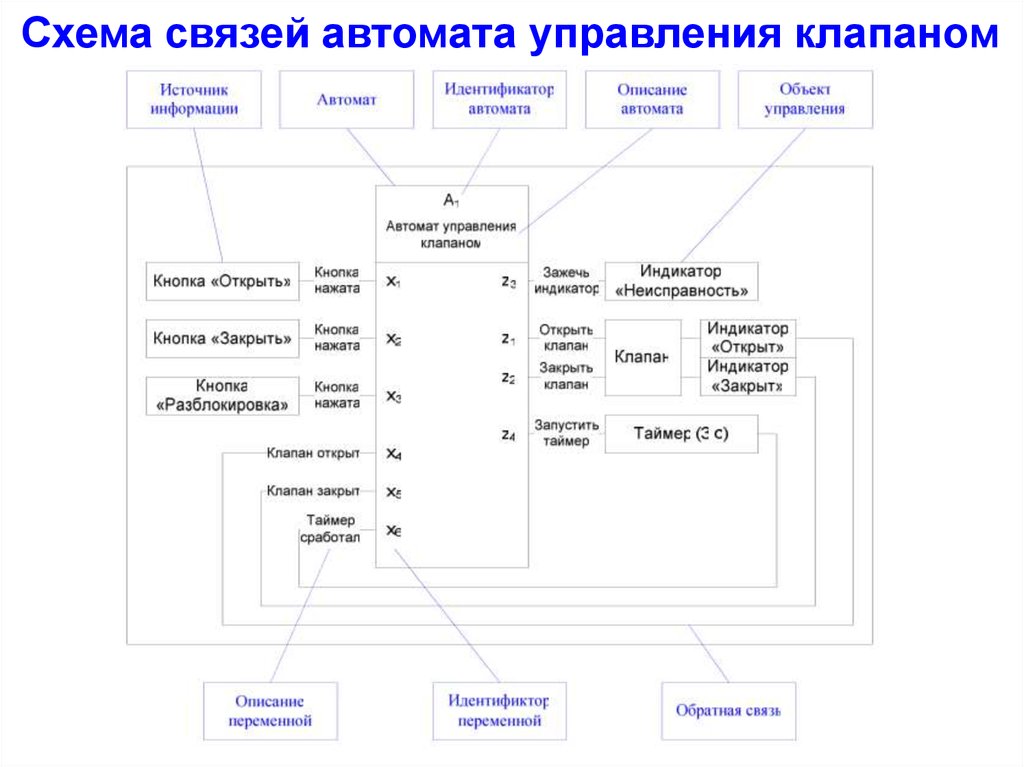
Схема связей автомата управления клапаном

51.

Схема связей автомата
«Часы с будильником»

52.

Типичные обозначения в графе состояний
структурного автомата
1. К дуге приписывается булево выражение, обозначающее условие
перехода в другое состояние. Если выражение громоздкое, то его
можно заменить кратким обозначением, а обозначение
расшифровать в другом месте.
2. Выходное воздействие отделяется от номера состояния (автомат
Мура) или условия перехода в другое состояние (автомат Мили)
горизонтальной или косой чертой.
3. Обычно используются краткие обозначения вида: Ai –автомат, ei
– событие, xi – входной сигнал, yi –выходной сигнал, Ci –
условие перехода.
4. Для того, чтобы обозначить приоритет при переходов в том
случае, когда выполняются условия перехода сразу на двух
ветвях, применяется обозначение приоритета с помощью
натурального числа, помещенного перед условием перехода и
отделенного от него двоеточием.
5. Переход «Иначе» необходим для того, чтобы пометить переход,
совершаемый, если не выполняются условия других переходов