Определение уравнения движения. Общий случай интегрального уравнения

1. Определение уравнения движения.

Общий случай интегрального уравнения
Способ Лебедева
1

2.

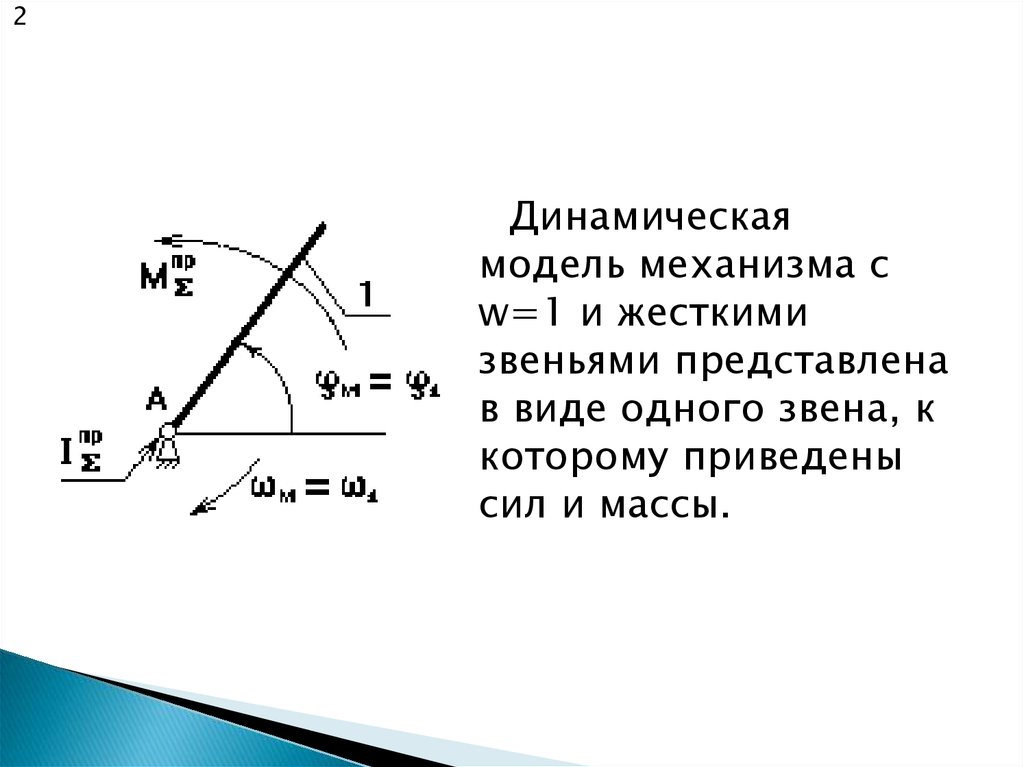
2
Динамическая
модель механизма с
w=1 и жесткими
звеньями представлена
в виде одного звена, к
которому приведены
сил и массы.

3.

3
Закон движения выбранного звена может быть
найден по приведенным параметрам динамической
модели
Теорема об изменении кинематической энергии :
Получаем:
нач
Где
нач нач
нач
2
2
d
,
dt
2
2
d
d 2
dt
dt 2

4.

4
Сумму работ можно представить в виде
интеграла с переменным верхним
пределом ψ от суммарного приведенного
момента по углу поворота, поэтому:
d
0

5.

5
Закон движения ω(ψ) звена приведения
представляет решение предыдущего
уравнения в виде функции обобщенной
координаты ψ
2
2
нач
2 нач

6.

6
Продифференцировав выражение суммы
работ по координате ψ, получим
дифференциальное уравнение движения:
d
2
d
2

7.

7
Учитывая, что нач const , получаем
дифференцированием
d
2d
2
угловое ускорение звена приведения
d d d
2
dt
dt
2 d
2
2

8.

8
МА можно представить как одно звено с
переменным моментом инерции, в общем
случае зависящим от обобщенной
координаты ψ.
Алгоритм расчета динамической модели
строиться в виде функции ψ(независимая
переменная).

9.

9
Свяжем расчетные значения ψ со временем.
Проинтегрируем и получим:
t
t
0
0
dt
При:
d
d
,
dt
d
d 2
dt
dt 2

10. Вывод

10
Определение соответствующих моментов
времени движения связано с
интегрированием обратной функции
1

11. Куандыкова С.С. ИБМ4-51

Литература:
1. Теория механизмов и машин(основы проектирования по
динамическим критериям и показателям
экономичности): учебное пособие/И.В.Леонов,
Д.И.Леонов. – М. : Высшее образование, Юрайт-Издат,
2009. – 239с. – (Основы наук)
2. http://tmm-umk.bmstu.ru/lectures/lect_6.htm
3. hoster.bmstu.ru/~rk2/e-fakul/prived_sil_mass.doc
11