Похожие презентации:
Пересечение поверхностей. (Лекция 7)
1. Лекция №7
Пересечение поверхностей прямой линией.Сечение поверхностей плоскостями.
Взаимное пересечение поверхностей
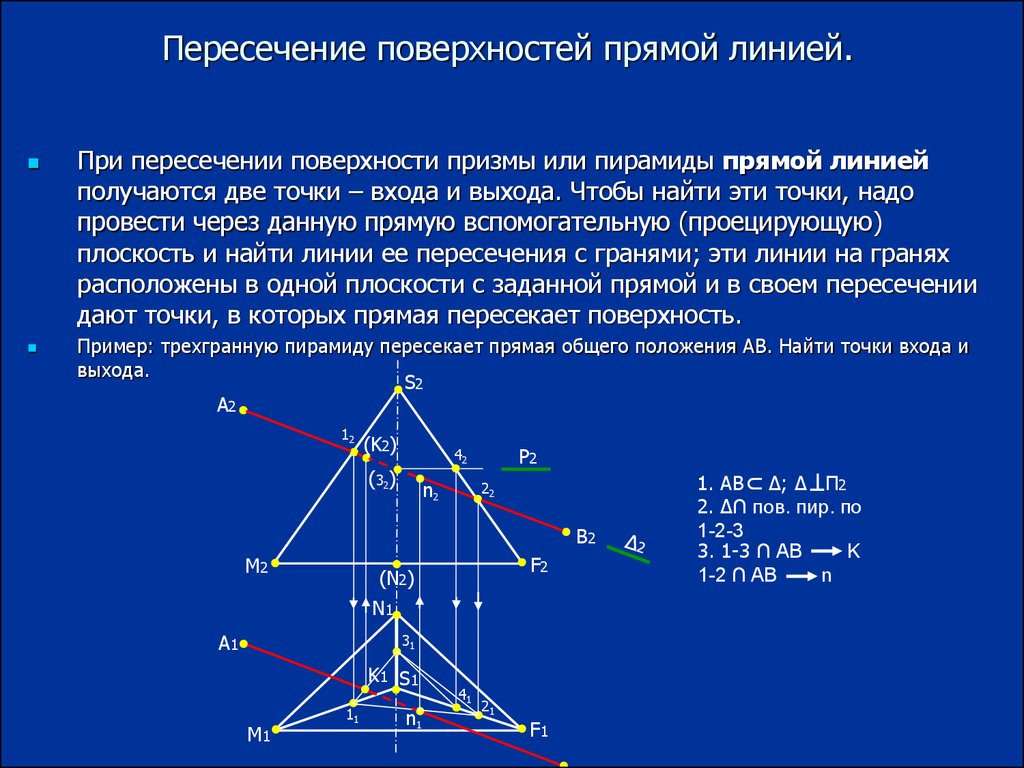
2. Пересечение поверхностей прямой линией.
При пересечении поверхности призмы или пирамиды прямой линиейполучаются две точки – входа и выхода. Чтобы найти эти точки, надо
провести через данную прямую вспомогательную (проецирующую)
плоскость и найти линии ее пересечения с гранями; эти линии на гранях
расположены в одной плоскости с заданной прямой и в своем пересечении
дают точки, в которых прямая пересекает поверхность.
Пример: трехгранную пирамиду пересекает прямая общего положения АВ. Найти точки входа и
выхода.
S2
А2
12
(K2)
P2
42
(32)
n2
22
В2
M2
F2
(N2)
N1
А1
31
K1 S1
M1
11
n1
41
1. АВ Δ; Δ П2
2. Δ∩ пов. пир. по
1-2-3
3. 1-3 ∩ АВ
K
1-2 ∩ AB
n
∩
21
F1
3.
При пересечении многогранника плоскостьюобразуется многоугольник, лежащий
в секущей плоскости. Его вершины – это точки пересечения ребер многогранника, а стороны – линии
пересечения его граней с секущей плоскостью. Т.о. задача сводится к построению точек пересечения
прямой с плоскостью и линий пересечения плоскостей.
При пересечении призмы с секущей плоскостью в зависимости от ее положения в сечении призмы
получается: 1. Многоугольник, параллельный и равный основанию, если секущая плоскость
параллельна основанию призмы; 2. Прямоугольник для прямой призмы (или параллелограмм для
наклонной), если секущая плоскость параллельна ребрам призмы; 3. Многоугольник, не равный и не
подобный основанию, если секущая плоскость наклонена к ребрам призмы.
Например, построить сечение прямой пятиугольной призмы секущей плоскостью Р, след которой
задан на виде слева.
Z
На эпюре прямоугольная призма
пересечена профильно-проецирующей плоскостью Р. Профильная
проекция фигуры сечения совпадает с профильным следом – проекцией Р3, обладающей собирательным свойством. Горизонтальные
проекции вершин многоугольника
сечения совпадают с горизонтальными проекциями соответствующих
ребер.
C2
C3
M2
(M3)
B2
B3
(A2)
(N2)
A3
Х
(A1)
(N1)
(B1)
(M1)
(C1)
Y1
(N3)
Y3
4.
Сечение поверхностей плоскостямиПри
разработке чертежей деталей часто возникает необходимость в построении сечений кривых деталей различными плоскостями. В общем случае
кривые поверхности пересекаются плоскостью по плоской кривой линии.
Отдельные точки, определяющие эту кривую, находятся способом вспомогательных плоскостей, который в данном случае заключается в следующем:
1.Вводится
вспомогательная плоскость, пересекающая кривую поверхность
по некоторой кривой линии, а данную плоскость – по прямой;
2.
Полученные прямая и кривая линии пересекаются в точках,
принадлежащих линии пересечения данной поверхности и плоскости;
3.
Используя несколько вспомогательных плоскостей, получают ряд точек,
достаточный для построения кривой пересечения.
Вспомогательные плоскости подбираются так, чтобы они пересекали
данную поверхность по простым линиям (прямым или окружностям). Среди
множества точек кривой пересечения выделяют опорные точки, занимающие
особые места на этой кривой: высшую и низшую, ближнюю и дальнюю,
точки наибольшей ширины кривой, точки видимости.
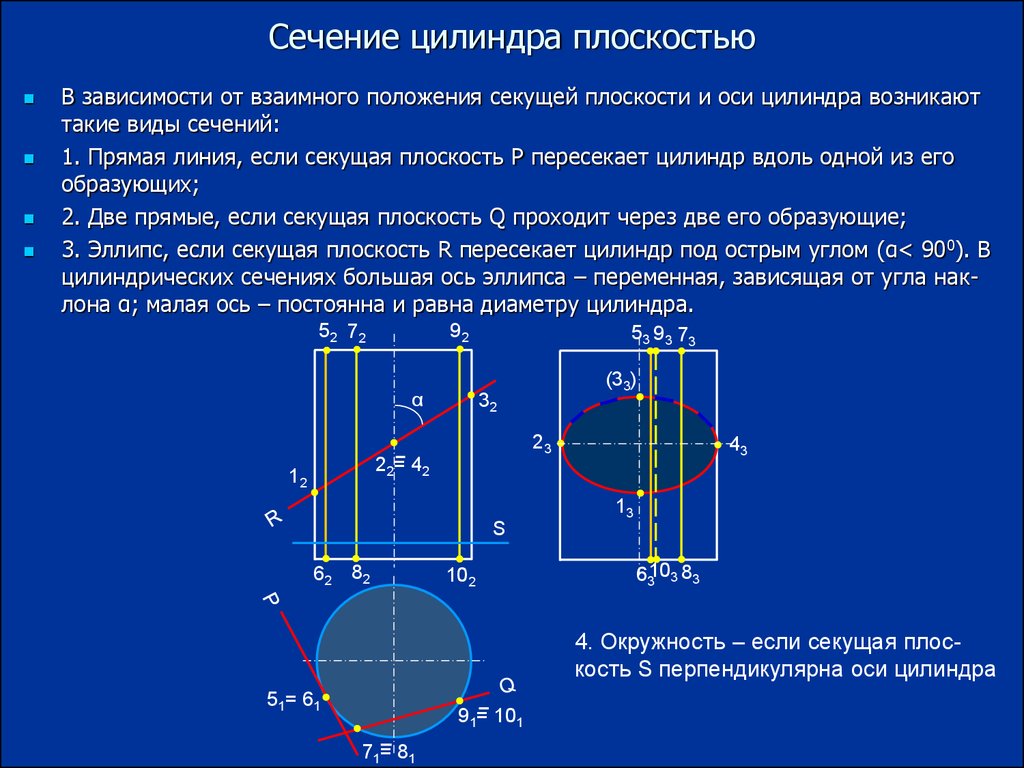
5. Сечение цилиндра плоскостью
В зависимости от взаимного положения секущей плоскости и оси цилиндра возникаюттакие виды сечений:
1. Прямая линия, если секущая плоскость Р пересекает цилиндр вдоль одной из его
образующих;
2. Две прямые, если секущая плоскость Q проходит через две его образующие;
3. Эллипс, если секущая плоскость R пересекает цилиндр под острым углом (α< 900). В
цилиндрических сечениях большая ось эллипса – переменная, зависящая от угла наклона α; малая ось – постоянна и равна диаметру цилиндра.
52 72
92
α
53 93 73
(33)
32
23
43
22= 42
12
13
S
62 82
102
63103 83
4. Окружность – если секущая плоскость S перпендикулярна оси цилиндра
51= 61
91= 101
71= 81
6. Сечение конуса плоскостью
В зависимости от направления секущей плоскости в сечении конуса могут быть:1. Окружность, если секущая плоскость Р параллельна основанию;
2. Треугольник, если секущая плоскость Q проходит через вершину конуса основанию;
3. Полный или усеченный эллипс, если секущая плоскость R пересекает конус под
острым углом к его оси;
4. Парабола, если секущая плоскость V параллельна одной из направляющих;
5. Гипербола, если секущая плоскость W параллельна двум направляющим.
Q
V
W
α
Р
7.
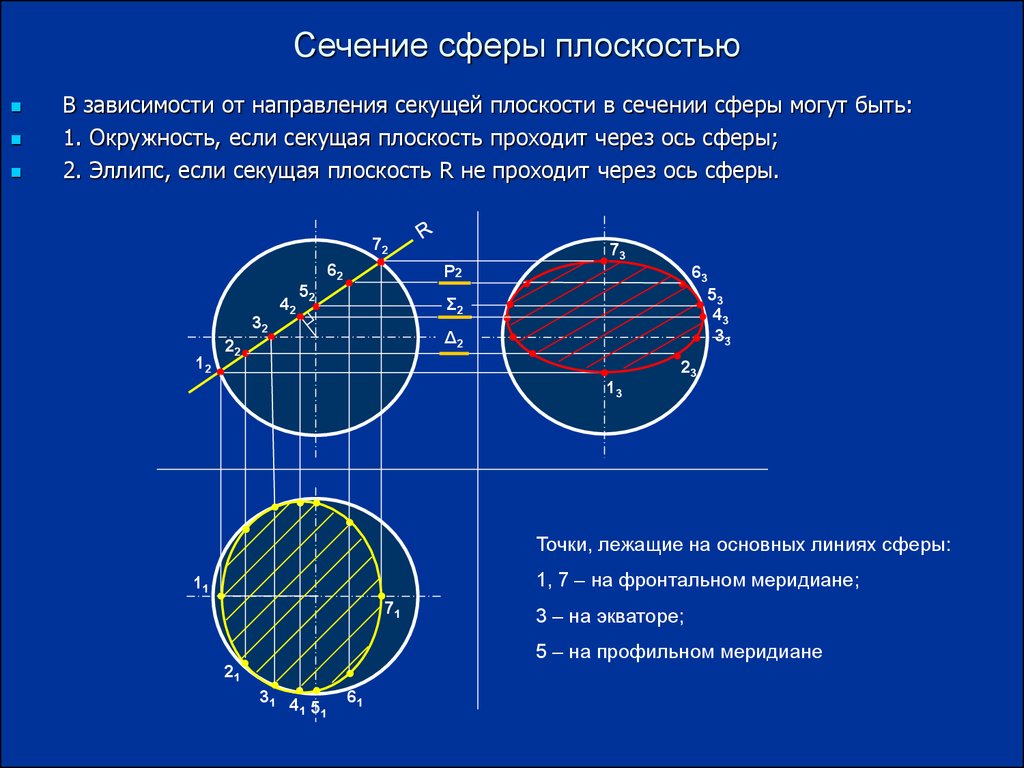
Сечение сферы плоскостьюВ зависимости от направления секущей плоскости в сечении сферы могут быть:
1. Окружность, если секущая плоскость проходит через ось сферы;
2. Эллипс, если секущая плоскость R не проходит через ось сферы.
72
Р2
62
32
12
42
73
52
63
53
43
33
Σ2
Δ2
22
23
13
Точки, лежащие на основных линиях сферы:
1, 7 – на фронтальном меридиане;
11
71
3 – на экваторе;
5 – на профильном меридиане
21
31
41 51
61
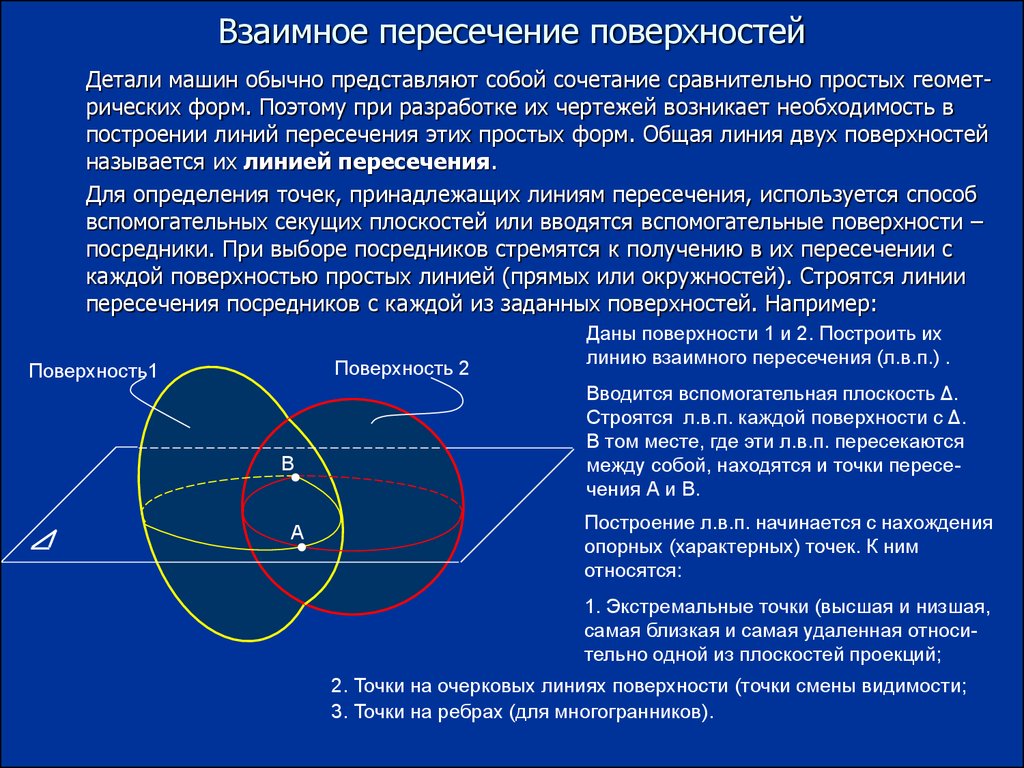
8. Взаимное пересечение поверхностей
Детали машин обычно представляют собой сочетание сравнительно простых геометрических форм. Поэтому при разработке их чертежей возникает необходимость впостроении линий пересечения этих простых форм. Общая линия двух поверхностей
называется их линией пересечения.
Для определения точек, принадлежащих линиям пересечения, используется способ
вспомогательных секущих плоскостей или вводятся вспомогательные поверхности –
посредники. При выборе посредников стремятся к получению в их пересечении с
каждой поверхностью простых линией (прямых или окружностей). Строятся линии
пересечения посредников с каждой из заданных поверхностей. Например:
Поверхность 2
Поверхность1
В
А
Даны поверхности 1 и 2. Построить их
линию взаимного пересечения (л.в.п.) .
Вводится вспомогательная плоскость Δ.
Строятся л.в.п. каждой поверхности с Δ.
В том месте, где эти л.в.п. пересекаются
между собой, находятся и точки пересечения А и В.
Построение л.в.п. начинается с нахождения
опорных (характерных) точек. К ним
относятся:
1. Экстремальные точки (высшая и низшая,
самая близкая и самая удаленная относительно одной из плоскостей проекций;
2. Точки на очерковых линиях поверхности (точки смены видимости;
3. Точки на ребрах (для многогранников).
9. Виды пересечения двух поверхностей
1. Обе поверхности многогранники: л.в.п. пространственная,замкнутая, ломаная;
2. Одна поверхность многогранник, другая – кривая: л.в.п. состоит из
звеньев пространственных замкнутых кривых;
3. Обе поверхности кривые: л.в.п. пространственная замкнутая
кривая.
При пересечении двух поверхностей возможны два случая:
а) полное пересечение (проницание) одной поверхности другой;
б) частичное взаимное пересечение поверхностей (врезка или врубка).
В первом случае л.в.п. распадается на две – линию очерка отверстия
входа и линию очерка отверстия выхода.
Во втором случае пересечение происходит по одной замкнутой линии.
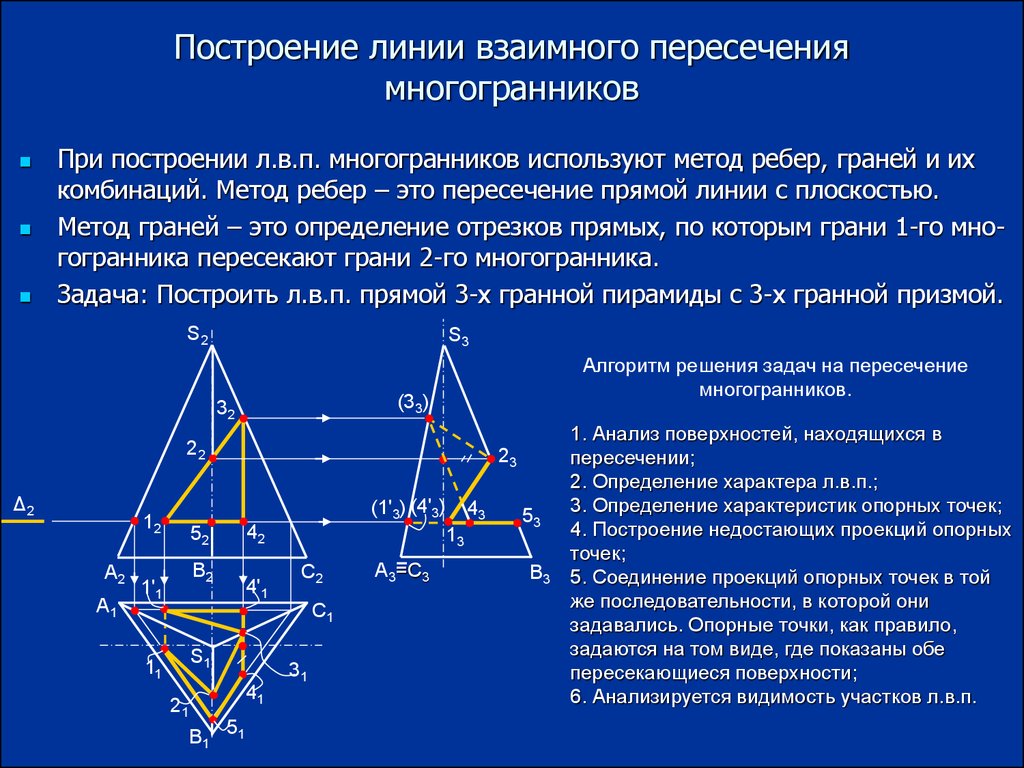
10. Построение линии взаимного пересечения многогранников
При построении л.в.п. многогранников используют метод ребер, граней и ихкомбинаций. Метод ребер – это пересечение прямой линии с плоскостью.
Метод граней – это определение отрезков прямых, по которым грани 1-го многогранника пересекают грани 2-го многогранника.
Задача: Построить л.в.п. прямой 3-х гранной пирамиды с 3-х гранной призмой.
S2
S3
Алгоритм решения задач на пересечение
многогранников.
(33)
32
22
Δ2
(1'3) (4'3)
12
A2
A1
23
52
B2
1'1
42
4'1
13
C2
C1
S1
11
21
31
41
B1 51
43
A3=C3
53
B3
1. Анализ поверхностей, находящихся в
пересечении;
2. Определение характера л.в.п.;
3. Определение характеристик опорных точек;
4. Построение недостающих проекций опорных
точек;
5. Соединение проекций опорных точек в той
же последовательности, в которой они
задавались. Опорные точки, как правило,
задаются на том виде, где показаны обе
пересекающиеся поверхности;
6. Анализируется видимость участков л.в.п.
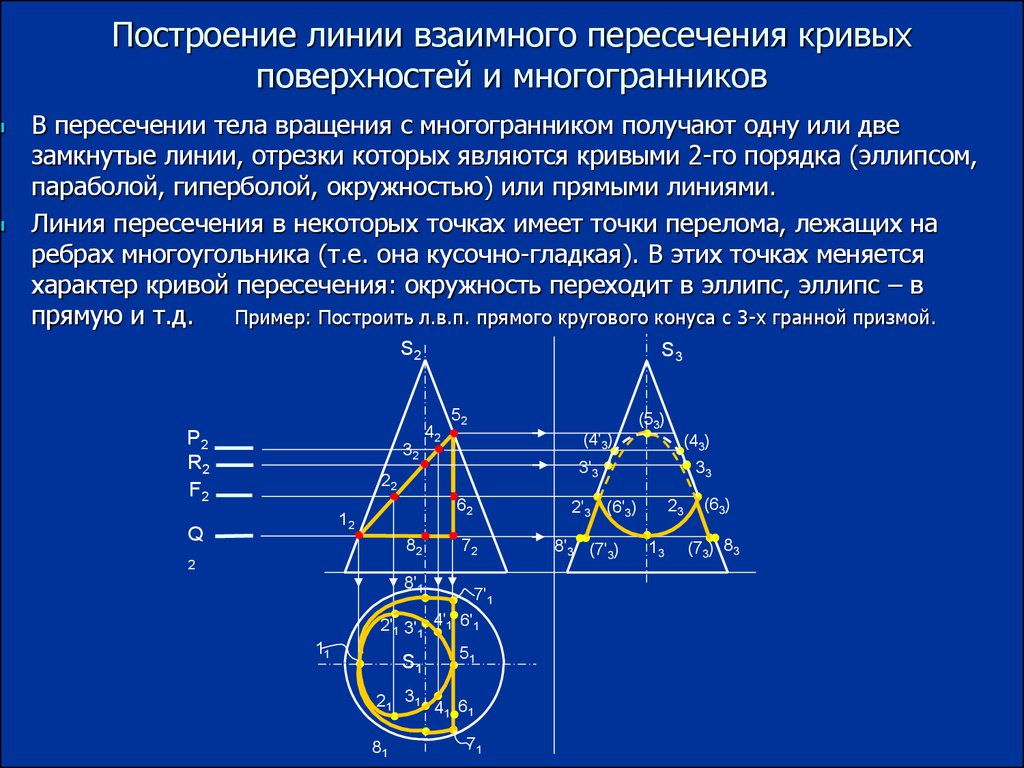
11. Построение линии взаимного пересечения кривых поверхностей и многогранников
В пересечении тела вращения с многогранником получают одну или двезамкнутые линии, отрезки которых являются кривыми 2-го порядка (эллипсом,
параболой, гиперболой, окружностью) или прямыми линиями.
Линия пересечения в некоторых точках имеет точки перелома, лежащих на
ребрах многоугольника (т.е. она кусочно-гладкая). В этих точках меняется
характер кривой пересечения: окружность переходит в эллипс, эллипс – в
прямую и т.д.
Пример: Построить л.в.п. прямого кругового конуса с 3-х гранной призмой.
S2
P2
R2
F2
32
S3
42
52
(53)
(4'3)
3'3
22
62
12
Q
82
72
7'1
2'1 3'1 4'1 6'1
11
S1
51
21 31 4 6
1
1
81
33
23
2'3 (6'3)
2
8'1
(43)
71
8'3 (7'3)
13
(63)
(73) 83
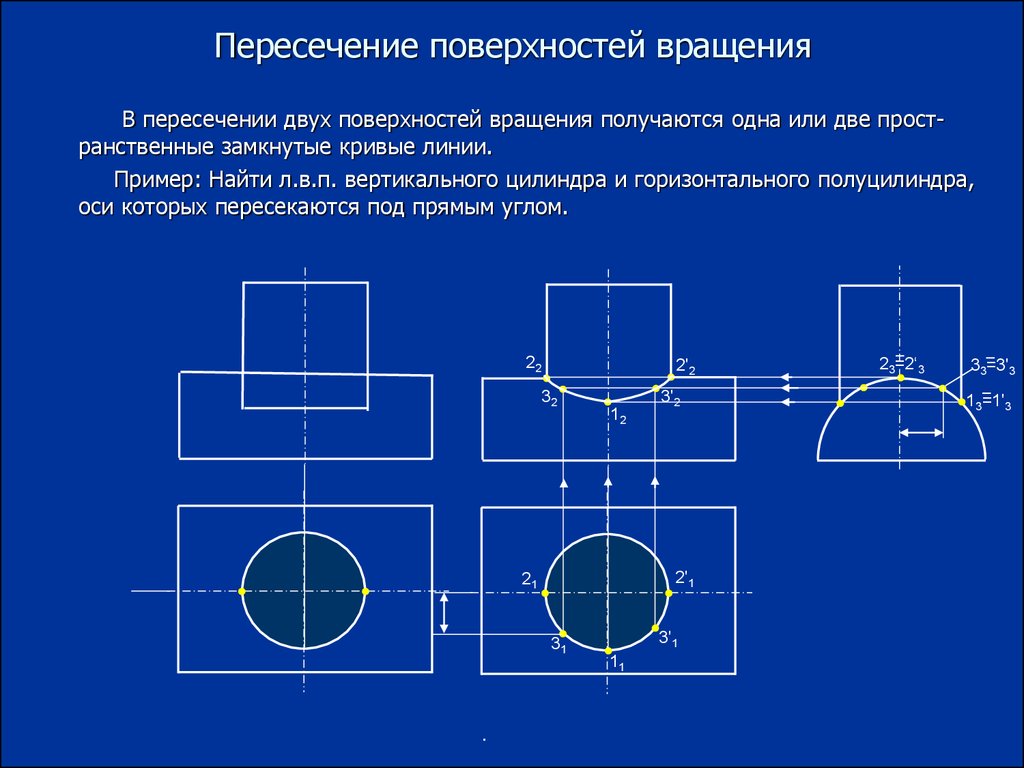
12. Пересечение поверхностей вращения
В пересечении двух поверхностей вращения получаются одна или две пространственные замкнутые кривые линии.Пример: Найти л.в.п. вертикального цилиндра и горизонтального полуцилиндра,
оси которых пересекаются под прямым углом.
22
2'2
32
12
2'1
21
31
.
3'2
3'1
11
23=2‘3
33=3'3
13=1'3





 Математика
Математика Инженерная графика
Инженерная графика








