Основные понятия механики

1. ОСНОВЫ МЕХАНИКИ

Лекция № 1

2. 1. ОСНОВНЫЕ ПОНЯТИЯ МЕХАНИКИ

Механика делится на три раздела:
1) кинематику;
2) динамику;
3) статику.
Кинематика изучает движение тел, не рассматривая
причины, которые это движение обусловливают.
Динамика изучает законы движения тел и причины,
которые вызывают или изменяют это движение.
Статика изучает законы равновесия системы тел. Если
известны законы движения тел, то из них можно
установить и законы равновесия. Поэтому законы статики
отдельно от законов динамики физика не рассматривает.
2

3.

Механика для описания движения тел в зависимости от
условий конкретных задач использует разные физические
модели. Простейшей моделью является материальная
точка - тело, обладающее массой, размерами которого в
данной задаче можно пренебречь. Совокупность
нескольких тел можно представить системой
материальных точек.
Под воздействием тел друг на друга тела могут
деформироваться, т. е. изменять свою форму и размеры.
Поэтому в механике вводится еще одна модель абсолютно твердое тело.
Абсолютно твердым называется тело, которое ни при
каких условиях не может деформироваться и при всех
условиях расстояние между двумя точками (или точнее
между двумя частицами) этого тела остается постоянным.
3

4.

Любое движение твердого тела можно представить как
комбинацию поступательного и вращательного движений.
Поступательное движение - такое, при котором любая
прямая, жестко связанная с движущимся телом, остается
параллельной своему первоначальному положению.
Вращательное движение - такое, при котором все точки тела
движутся по окружностям, центры которых лежат на одной и
той же прямой, называемой осью вращения.
Движение тел происходит в пространстве и во времени.
Система отсчета - совокупность
системы координат и часов, связанных
с телом отсчета. В декартовой системе
координат положение точки А в данный
момент времени характеризуется тремя
координатами x, y, z или радиусомвектором r, проведенным из начала
системы координат в данную точку.
4

5.

1.1. Траектория, длина пути, вектор
перемещения
При движении материальной точки ее координаты с
течением времени изменяются. В общем случае ее
движение определяется скалярными уравнениями
x = x(t),
у = y(t),
(1.1)
z = z(t),
эквивалентными векторному уравнению
r = r(t).
(1.2)
Уравнения (1.1) и (1.2) называются кинематическими
уравнениями движения материальной точки.
5

6.

1.2. Скорость
Для характеристики движения
материальной точки вводится
векторная величина - скорость,
которая определяет как
быстроту движения, так и
его направление в данный
момент времени.
Вектором средней скорости <v> называется отношение
приращения Dr радиуса-вектора точки к промежутку
времени Dt
Dr
v
.
(1.3)
Dt
6

7.

Пример
1. Половину времени тело двигалось со скоростью V1, а вторую
половину – со скоростью V2. Какова средняя скорость тела?
Решение
Вычислим суммарный путь, пройденный телом, обозначив t общее время движения:
S = V1·t /2 + V2·t /2 = (V1 + V2) ·t /2.
Разделив на t, получаем среднюю скорость:
<V> = (V1 + V2)·/2.
2. Изменим условие задачи. Половину пройденного
расстояния тело двигалось со скоростью V1, а вторую
половину – со скоростью V2. Какова средняя скорость тела?
Решение
Вычислим суммарное время движения: t = t1 + t2, где
t1 = S/(2·V1), t2 = S/(2·V2) – времена движения на 1 и 2 участках.
Тогда
<V> = S/(S/(2·V1) + S/(2·V2)) = 2·V1·V2 /(V1 + V2).
7

8.

При неограниченном уменьшении D t средняя скорость
стремится к предельному значению, которое называется
мгновенной скоростью
Dr dr
v lim
.
Dt 0 Dt
dt
По мере уменьшения D t перемещение D s все больше будет
приближаться к |D r|, поэтому модуль мгновенной скорости
Dr
Dr
Ds ds
lim
lim
lim
.
Dt 0 Dt
Dt 0 Dt
Dt 0 Dt
dt
Если выражение ds = v·dt проинтегрировать по времени в
пределах от t до t + D t, то найдем перемещение точки за
время D t:
t Dt
s
·dt.
t
8

9. 1.3. Ускорение и его составляющие

Средним ускорением неравномерного движения в
интервале от t до t+Dt называется векторная величина,
равная отношению изменения скорости Dv к интервалу
времени Dt
<a> = Dv /Dt.
Мгновенным ускорением а материальной точки в момент
времени t будет предел среднего ускорения
Dv dv
a lim a lim
.
Dt 0
Dt 0 Dt
dt
Таким образом, ускорение а есть векторная величина,
равная первой производной скорости по времени.
9

10.

Полное ускорение тела есть
геометрическая сумма
тангенциальной и
нормальной составляющих:
dv
a
a a n
dt
Тангенциальная составляющая ускорения равна первой
производной модуля скорости по времени, определяя тем
самым быстроту изменения скорости по модулю.
D
D d
a lim
Dt 0
Dt
lim
Dt 0
Dt
dt
.
Нормальная составляющая ускорения направлена по
нормали к траектории к центру ее кривизны (поэтому ее
называют также центростремительным ускорением).
D n
a n lim
.
Dt 0 Dt
r
2
10

11.

Пример
Диск радиусом R = 10 см вращается равноускоренно с
тангенциальным ускорением a = 1,5 м/с2. Определить
полное ускорение точки на ободе диске в момент времени
t = 2 c.
Решение
Скорость точки в момент t = 2 c:
v = a ·t = 1,5·2 = 3 м/с.
Нормальное ускорение в этот
момент:
an = v2/R = 1,52/0,1 = 22,5 м/с2.
Полное ускорение определяем так:
a an2 a 2 1,52 22,52 22,7 м/с 2 .
11

12. 1.4. Угловая скорость и угловое ускорение

Пусть некоторая точка движется по окружности радиуса
R. Ее положение через промежуток времени Dt зададим
углом D .
Угловой скоростью называется векторная величина,
равная первой производной угла поворота тела по
времени:
D d
lim
.
Dt 0
Dt
dt
Линейная скорость точки связана
с угловой скоростью соотношением
v = R· .
12

13.

Если = const, то вращение равномерное и его можно
характеризовать периодом вращения Т - временем, за
которое точка совершает один полный оборот, т. е.
поворачивается на угол 2 :
Т = 2 / .
Число полных оборотов, совершаемых телом при
равномерном его движении по окружности, в единицу
времени называется частотой вращения
n = 1/T = /(2· ).
Таким образом,
= 2· ·n.
Угловым ускорением называется векторная величина,
равная первой производной угловой скорости по времени:
d
.
dt
При вращении тела вокруг неподвижной оси вектор
углового ускорения направлен вдоль оси вращения в
сторону вектора элементарного приращения угловой
скорости.
13

14.

Тангенциальная составляющая ускорения
a = dv/dt = d( ·R)/dt =R·d /dt = R· .
Нормальная составляющая ускорения
2 2R2
an
2 R.
R
R
Связь между линейными (длина пути s, линейная
скорость v, тангенциальное ускорение а , нормальное
ускорение аn) и угловыми величинами (угол поворота D ,
угловая скорость , угловое ускорение ) выражается
следующими формулами:
s R· , R· , a R· , an 2 ·R.
В случае равнопеременного движения точки по
окружности ( = const)
0 ·t , 0 ·t ·t 2 / 2,
где 0 - начальная угловая скорость.
14

15. 1.5. Кинематические уравнения как закон движения

Закон движения - исчерпывающая характеристика
характера перемещения тела (материальной точки) в
пространстве. В случае постоянства действующих сил
закон поступательного движения в декартовой системе
координат имеет вид: x x V t a t 2 ;
0
x0
x
2
t2
y y0 V y0 t a y ;
2
t2
z z0 Vz0 t a z .
2
Дифференцируя по t, получаем
Vx Vx0 a x t;
V y V y0 a y t;
Vz Vz0 a z t.
15

16.

Повторное дифференцирование приводит к выражениям
аx ax;
аy ay;
аz az .
Выполняя указанные действия в обратном порядке
(интегрируя составляющие ускорения), можно получить
составляющие скорости, а проинтегрировав последние –
перемещения по осям OX, OY и OZ. Эта идея лежит в основе
функционирования инерциальных навигационных систем.
Модуль скорости и модуль ускорения получают из
выражений:
V
Vx2 Vy2 Vz2 ;
a
a x2 a y2 a z2 .
Суммарное перемещение (не путь!) можно найти с помощью
подобной формулы
2
2
2
D
( xК x0 ) ( yК y0 ) ( zК z0 ) .
16

17.

Пример
Закон движения материальной точки имеет вид
x 2 4 t 0,3 t 2 ;
y 5 2 t 0,6 t 2 ;
z 4 3 t.
Определите модуль скорости и полное ускорение материальной
точки в момент времени t = 3 c.
Решение.
После однократного дифференцирования получаем:
Vx 4 0,6 t , ( м / с);
V y 2 1,2 t , ( м / с);
Vz 3, ( м / с).
17

18.

Еще раз дифференцируем:
a x 0,6, ( м / с 2 );
a y 1,2, ( м / с 2 );
a z 0.
Решения для модуля скорости и полного ускорения при
t = 3 c имеют вид:
V
5,82 ( 1,6) 2 ( 3) 2z 6,72 ( м / с);
a
0,6 2 ( 1,2) 2 0 2 1,34 ( м / с 2 ).
18

19. 2. ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ И ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА 2.1. Первый закон Ньютона. Масса. Сила

Всякая материальная точка (тело) сохраняет состояние
покоя или равномерного прямолинейного движения до тех
пор, пока воздействие со стороны других тел не заставит
ее изменить это состояние.
Первый закон Ньютона выполняется не во всякой системе
отсчета, а те системы, по отношению к которым он
выполняется, называются инерциальными системами
отсчета.
Масса тела - физическая величина, являющаяся одной из
основных характеристик материи, определяющая ее
инерционные (инертная масса) и гравитационные
(гравитационная масса) свойства.
19

20.

Чтобы описывать воздействия, упоминаемые в первом законе
Ньютона, вводят понятие силы. Сила - это векторная
величина, являющаяся мерой механического воздействия
на тело со стороны других тел или полей, в результате
которого тело приобретает ускорение или изменяет свою
форму и размеры.
2.2. Второй закон Ньютона
Он же - основной закон динамики поступательного
движения: ускорение, приобретаемое материальной
точкой (телом), пропорционально вызывающей его силе,
совпадает с нею по направлению и обратно
пропорционально массе материальной точки (тела)
а = F/m,
или
F = m·а = m·dv/dt.
20

21.

Учитывая, что масса материальной точки в классической
механике есть величина постоянная, ее можно внести под
знак производной:
F = d(m·v)/dt.
Векторная величина
р = m·v,
называется импульсом (количеством движения) этой
материальной точки.
Тогда
F = dp/dt.
Это выражение - более общая формулировка второго
закона Ньютона: скорость изменения импульса
материальной точки равна действующей на нее силе.
Единица силы в СИ - ньютон (Н): 1 Н - сила, которая
массе 1 кг сообщает ускорение 1 м/с2 в направлении
действия силы:
1 Н = 1 кг·м/с2.
21

22.

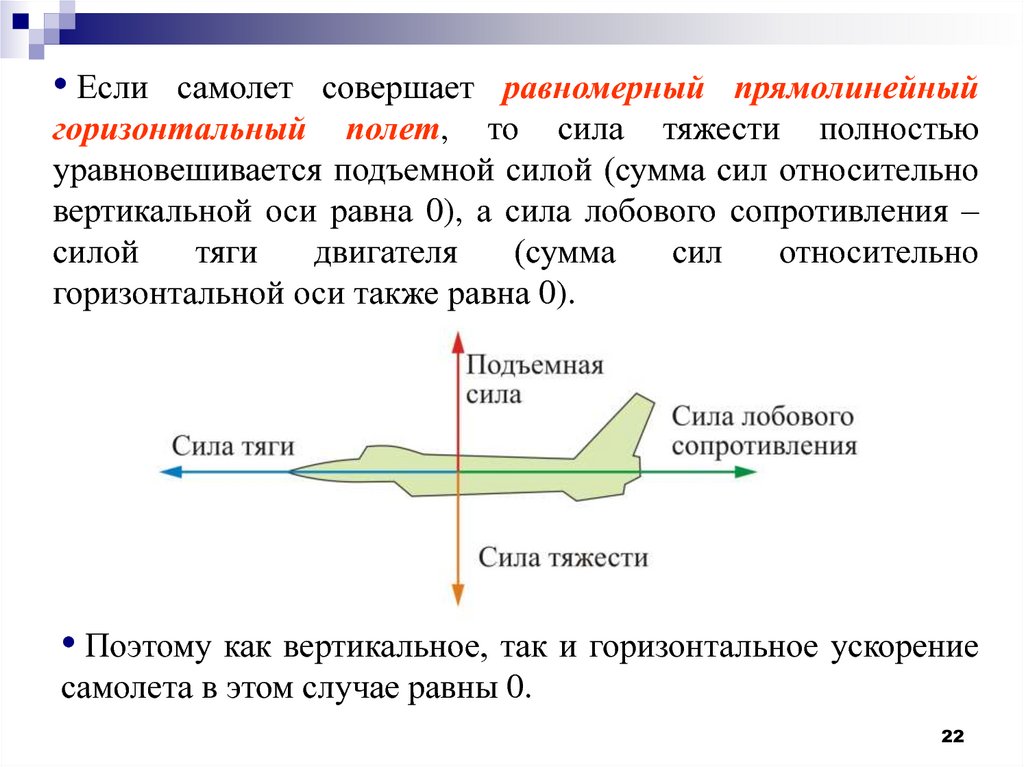
• Если
самолет совершает равномерный прямолинейный
горизонтальный полет, то сила тяжести полностью
уравновешивается подъемной силой (сумма сил относительно
вертикальной оси равна 0), а сила лобового сопротивления –
силой
тяги
двигателя
(сумма
сил
относительно
горизонтальной оси также равна 0).
• Поэтому как вертикальное, так и горизонтальное ускорение
самолета в этом случае равны 0.
22

23.

Пример
С башни брошен камень в горизонтальном направлении с
начальной скоростью 40 м/с. Какова скорость камня через
3 с после начала движения? Какой угол образует вектор
скорости камня с плоскостью горизонта в этот момент?
Дано: v0 = 40 м/с, t = 3 c, g = 9,81 м/с2, vг = v0, vв = 0.
Найти: v, a.
Решение.
Введем систему координат: ось ОХ направим
горизонтально, а ось OY – вертикально вниз.
Вдоль оси ОХ после броска камня никакие силы не
действуют (пренебрегаем сопротивлением воздуха),
поэтому ускорение вдоль этой оси равно нулю:
ax = 0.
23

24.

Вдоль оси OY вниз действует сила тяжести FT = mg, поэтому
ускорение вдоль этой оси по второму закону Ньютона равно
ay = mg/m = g,
где g – ускорение свободного падения.
В момент времени t = 3 с вертикальная составляющая
скорости камня vв будет равна
vв = gt = 9,81·3 = 29,43 (м/с).
Так как vг не меняется (ax = 0), то скорость v будет равна
v vг2 vв2 40 2 29,432 49,66 ( м / с) .
Результирующая скорость составляет с плоскостью
горизонта угол
vв
.
a arcsin
arcsin 0,593 36 .
v
■
24

25.

2.3. Третий закон Ньютона
Всякое действие материальных точек (тел) друг на
друга носит характер взаимодействия; силы, с
которыми действуют друг на друга материальные
точки, всегда равны по модулю, противоположно
направлены и действуют вдоль прямой, соединяющей
эти точки:
F12 = - F21,
где F12 - сила, действующая на первую материальную
точку со стороны второй;
F21 - сила, действующая на вторую материальную точку со
стороны первой. Эти силы приложены к разным
материальным точкам (телам), всегда действуют парами и
являются силами одной природы.
Третий закон Ньютона позволяет осуществить
переход от динамики отдельной материальной точки
к динамике системы материальных точек.
25

26.

Пример
F13
F11
F22
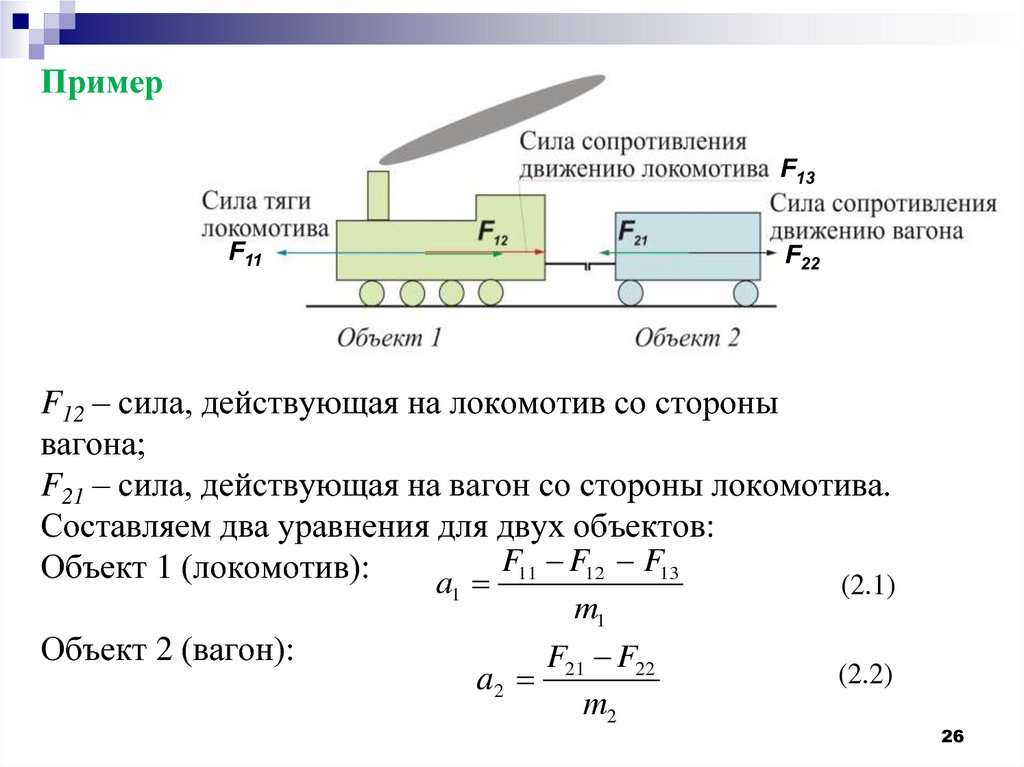
F12 – сила, действующая на локомотив со стороны
вагона;
F21 – сила, действующая на вагон со стороны локомотива.
Составляем два уравнения для двух объектов:
F11 F12 F13
Объект 1 (локомотив):
a
(2.1)
1
Объект 2 (вагон):
m1
F F22
a2 21
m2
(2.2)
26

27.

При определении сил в сцепке (F12 и F21) учтем, что они
равны по величине (по третьему закону Ньютона) и
противоположны по направлению (F12 = -F21) .
Кроме того, считая сцепку жесткой, полагаем, что
ускорения локомотива и вагона одинаковы (а1 = а2 = a).
Тогда можно приравнять правые части уравнений (2.1) и
(2.2), заменив в правой части F21 на F12.
F11 F12 F13 F12 F22
.
m1
m2
Разрешая уравнение относительно F12, получаем
F12 = (m2 F11 + m1 F22 – m2 F13)/(m1 + m2).
Затем из уравнения (2.1) или (2.2) определяем ускорение
системы a.
27

28. Вопросы, выносимые на семинар

1. Траектория, длина пути, вектор перемещения.
2. Средняя и мгновенная скорость. Ускорение и его
составляющие.
3. Угловая скорость и угловое ускорение.
4. Кинематические уравнения как законы движения.
5. Первый закон Ньютона. Понятия массы и силы.
6. Второй закон Ньютона.
7. Третий закон Ньютона.
28