Центральные и вписанные углы

1. Центральные и вписанные углы

ИРКУТСКАЯ ОБЛАСТЬ
УСОЛЬСКИЙ РАЙОН
МБОУ «МИШЕЛЁВСКАЯ СОШ № 19»
Центральные и
вписанные углы
Геометрия 8 класс, Атанасян Л.С.
Выполнила Сахарова Марина Александровна

2. Игра «Верю-не верю»

1. Верите ли вы, что окружность – это геометрическая фигура, состоящая
из всех точек плоскости, расположенных на заданном расстоянии?
2. Верите ли вы, что хорда – это отрезок, соединяющий две точки
окружности?
3. Верите ли вы, что отрезок, соединяющий центр окружности с какойлибо точкой окружности называется диаметром
4. Верите ли вы, что любые две точки окружности делят ее на две дуги?
5. Верите ли вы, что прямая и окружность могут иметь одну, две, три
общие точки?

3. Игра «Верю-не верю»

6. Верите ли вы, что угол – это геометрическая фигура, которая состоит
из точки и двух лучей?
7. Верите ли вы, что любой угол разделяет плоскость на две части?
8. Верите ли вы, что угол, обе стороны которого лежат на одной прямой
называется развернутым?
9. Верите ли вы, что градусная мера прямого угла равна 90º, а градусная
мера развернутого угла равна 180º?
10. Верите ли вы, что градусная мера острого угла больше градусной меры
прямого угла, а градусная мера тупого угла меньше градусной меры
развернутого угла?

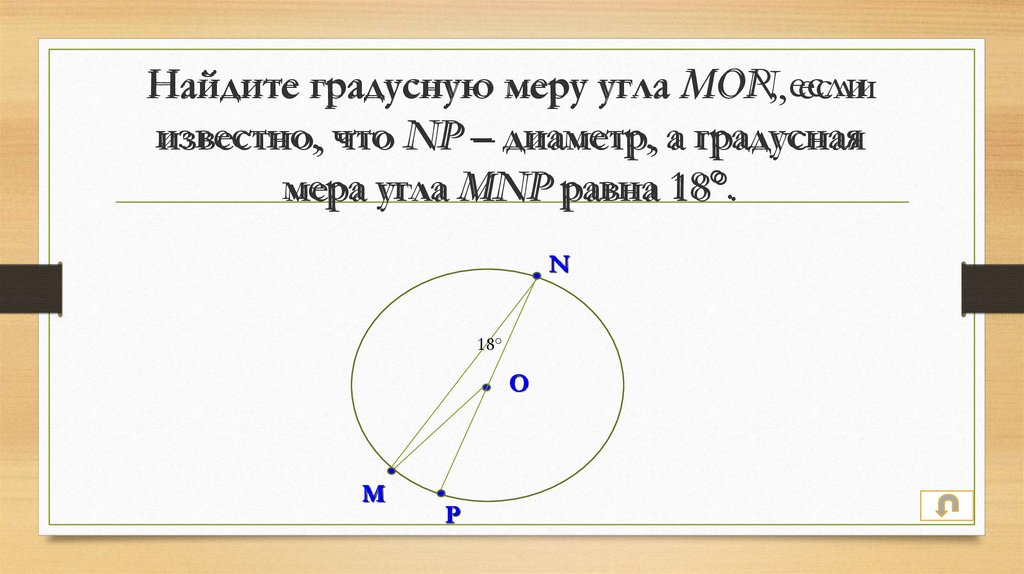
4. Найдите градусную меру угла MON, если известно, что NP – диаметр, а градусная мера угла MNP равна 18°.

Найдите градусную меру угла MON,
MOP, если
если
известно, что NP – диаметр, а градусная
мера угла MNP равна 18°.
N
18°
О
M
P

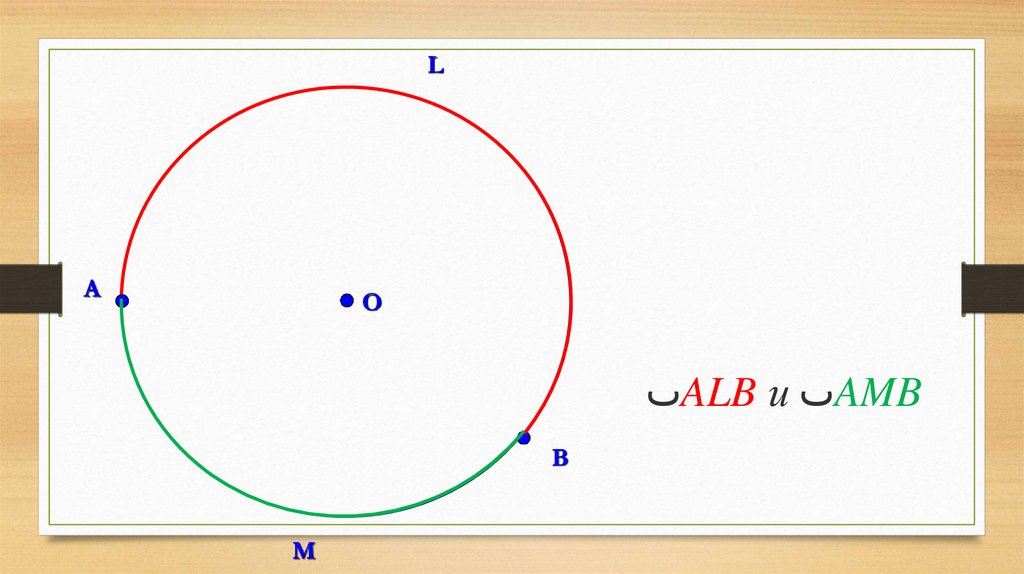
5.

L
А
О
‫ٮ‬ALB и ‫ٮ‬AMB
В
M

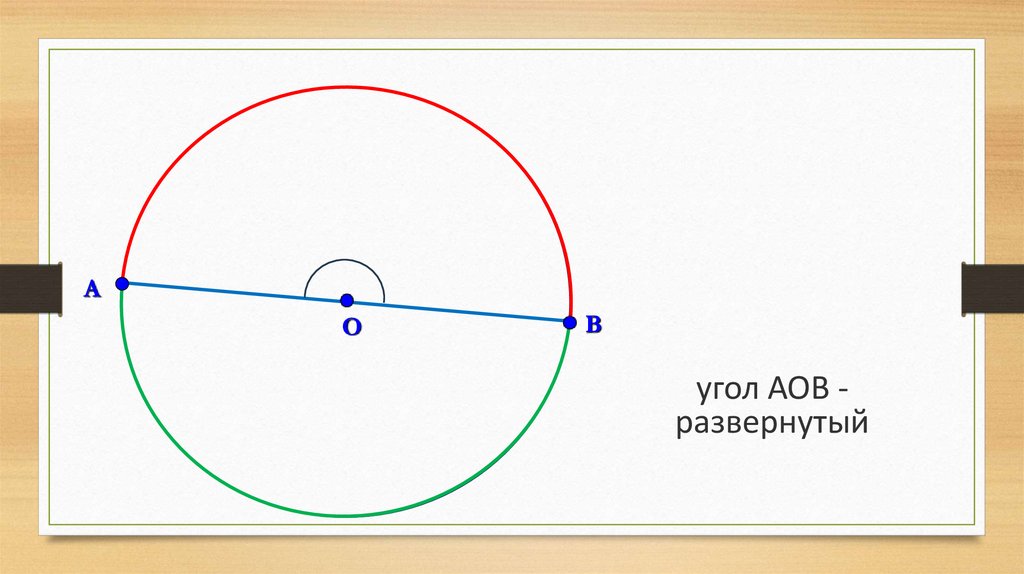
6.

А
О
В
угол АОВ развернутый

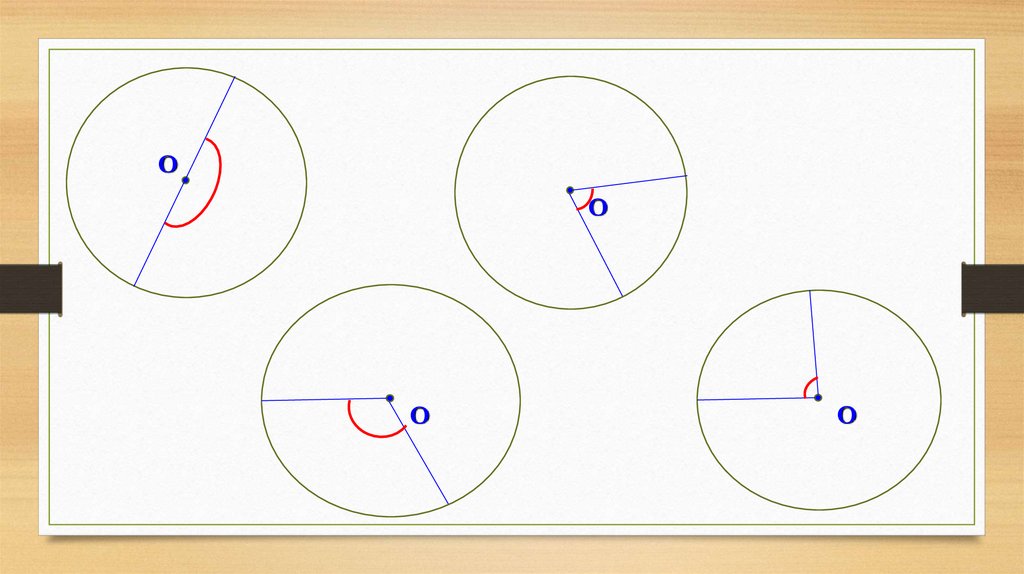
7.

О
О
О
О

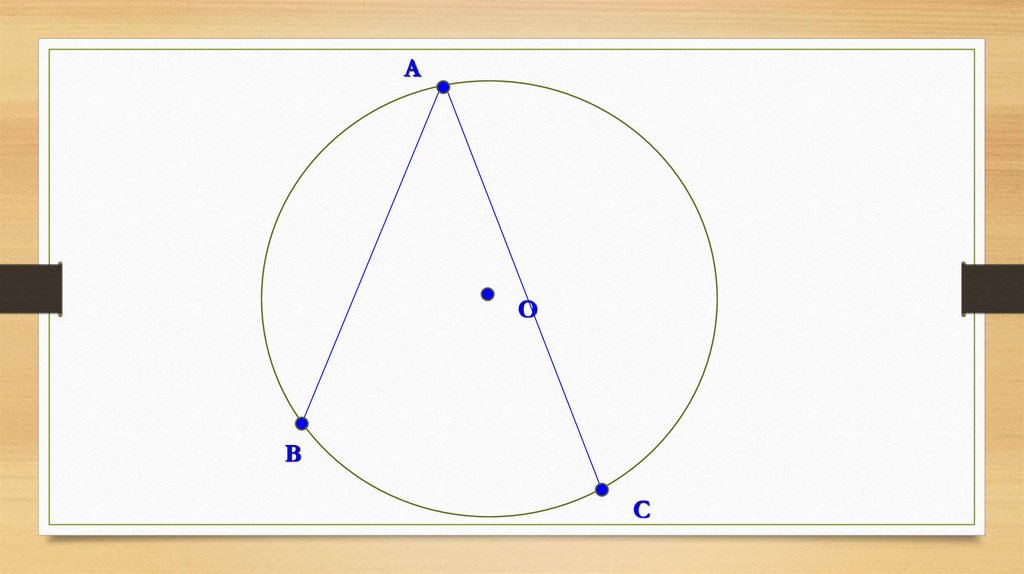
8.

А
О
В
С

9.

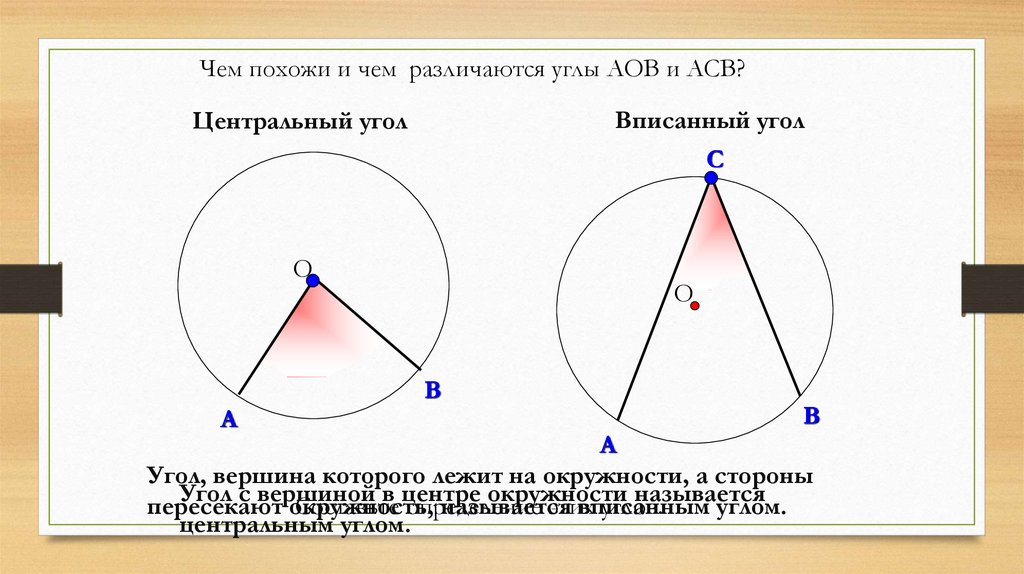
Чем похожи и чем различаются углы АОВ и АСВ?
Вписанный угол
Центральный угол
С
О
О
В
А
В
А
Угол, вершина которого лежит на окружности, а стороны
Угол с вершиной в центре окружности называется
Составьте определение
этих
углов.
пересекают окружность,
называется
вписанным
углом.
центральным углом.

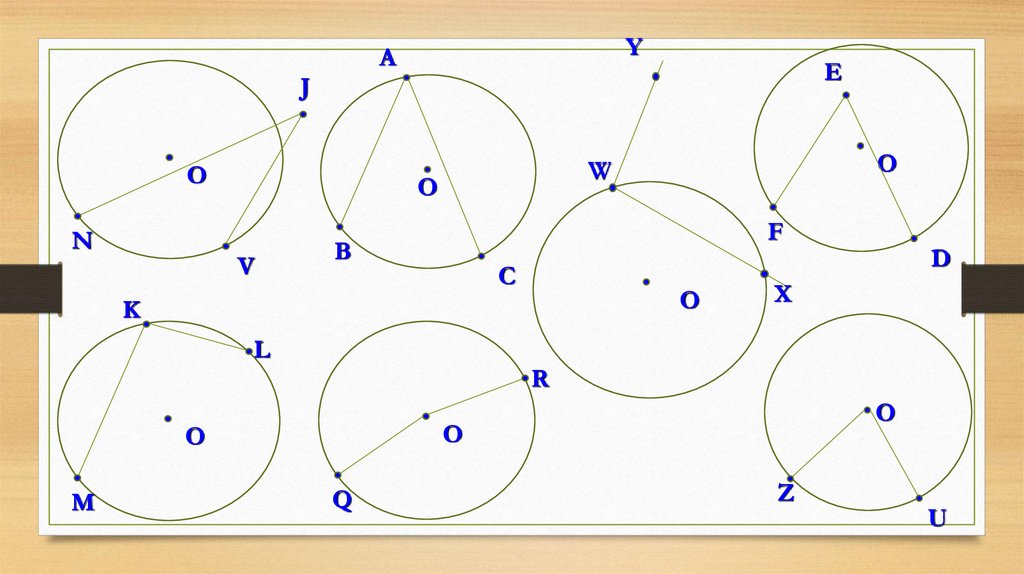
10.

Y
А
Е
J
О
N
О
V
О
W
F
В
С
О
K
D
X
L
R
О
О
M
О
Q
Z
U

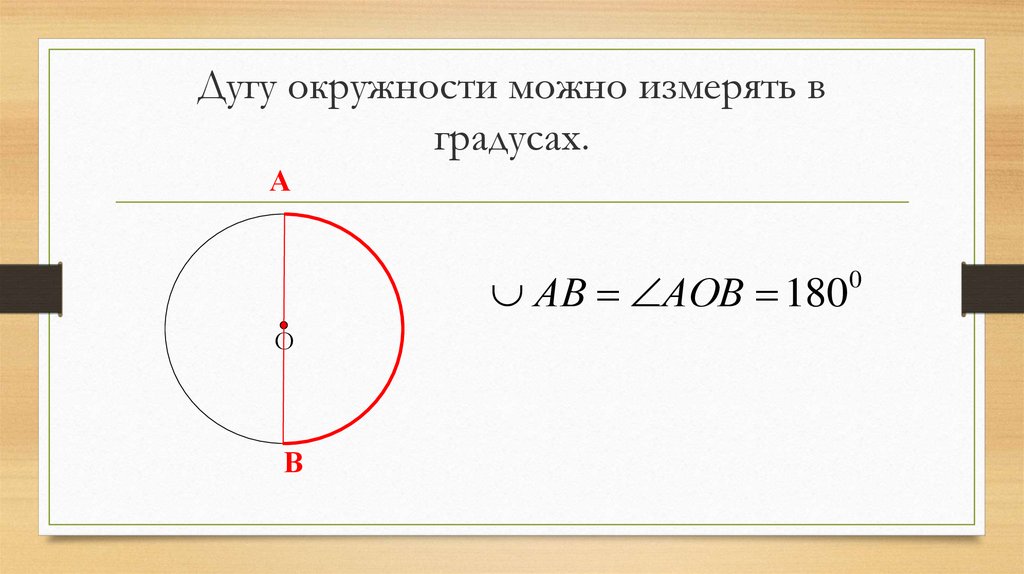
11. Дугу окружности можно измерять в градусах.

А
АВ АОВ 180
О
В
0

12.

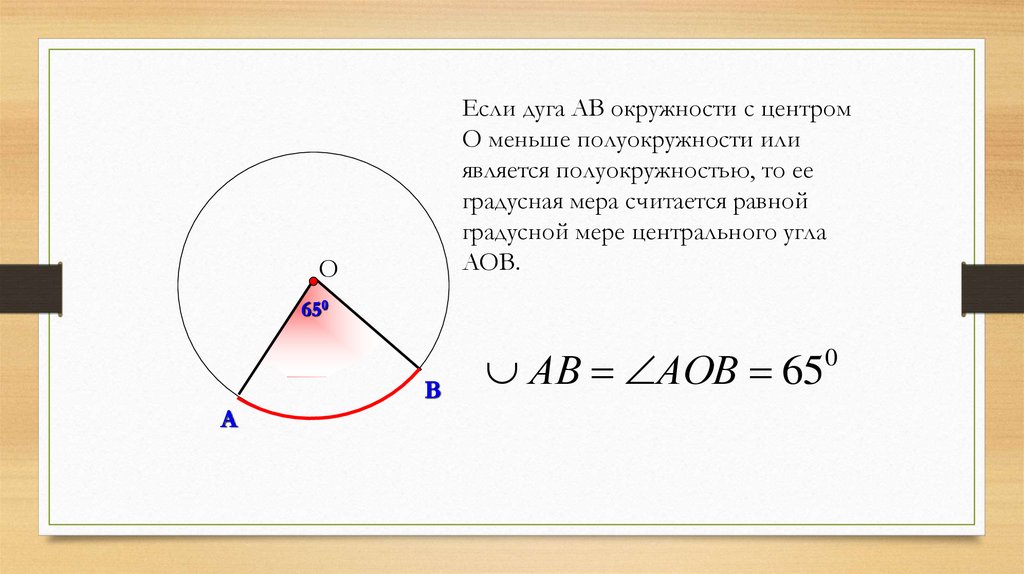
Если дуга АВ окружности с центром
О меньше полуокружности или
является полуокружностью, то ее
градусная мера считается равной
градусной мере центрального угла
АОВ.
О
650
В
А
АВ АОВ 65
0

13.

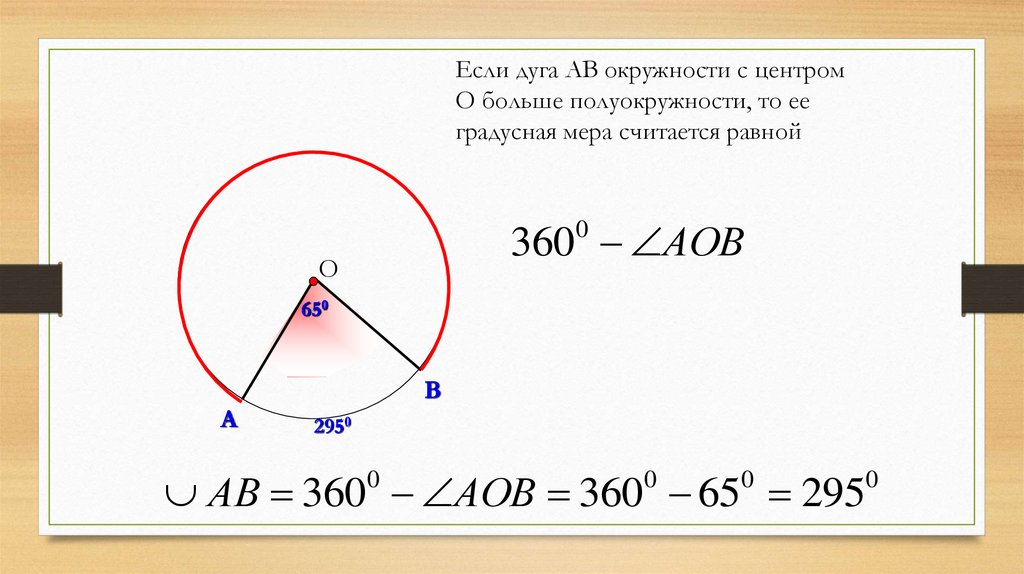
Если дуга АВ окружности с центром
О больше полуокружности, то ее
градусная мера считается равной
360 АОВ
0
О
650
В
А
2950
АВ 360 АОВ 360 65 295
0
0
0
0

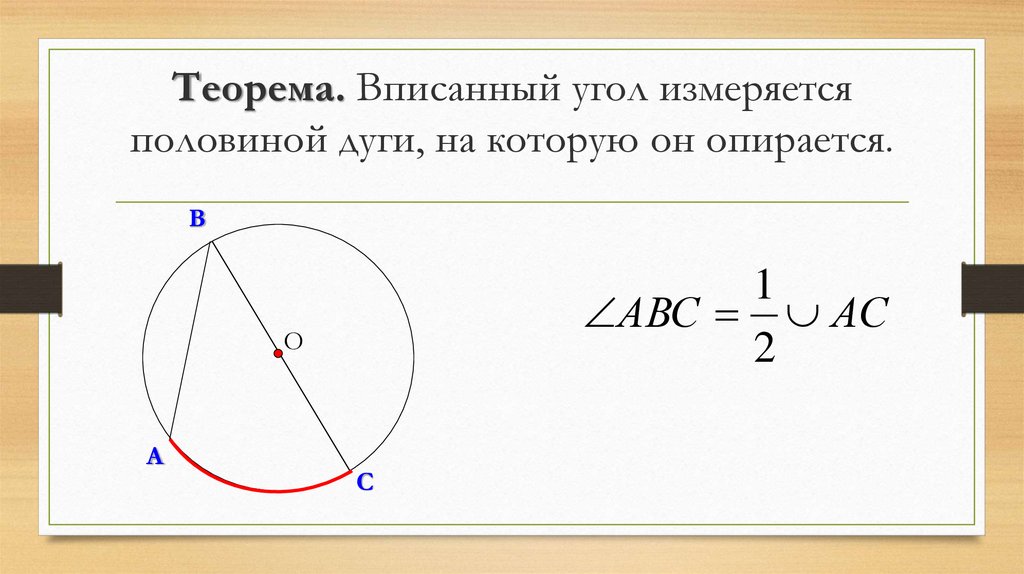
14. Теорема. Вписанный угол измеряется половиной дуги, на которую он опирается.

В
1
АВС АС
2
О
А
С

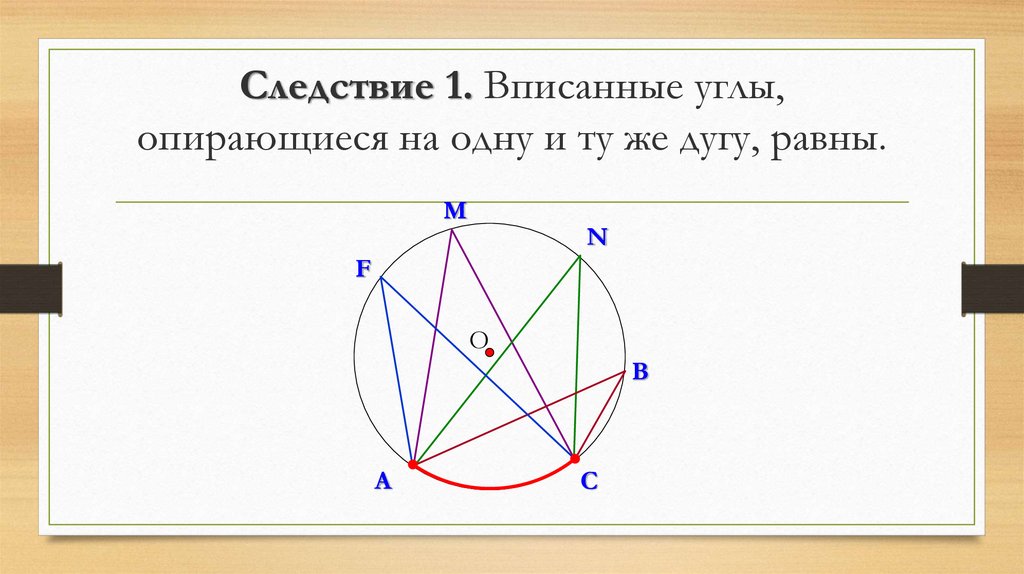
15. Следствие 1. Вписанные углы, опирающиеся на одну и ту же дугу, равны.

M
N
F
О
В
А
С

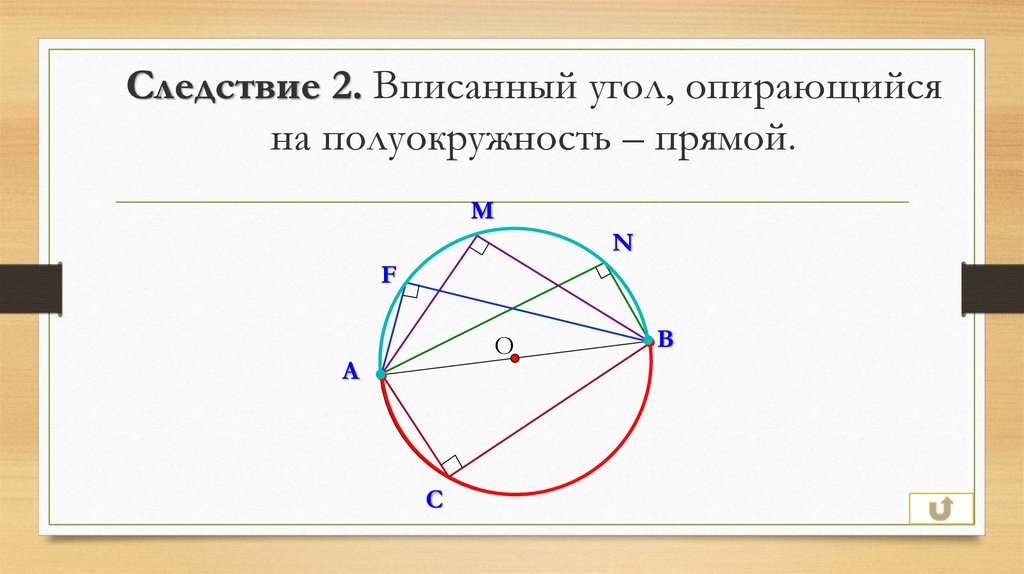
16. Следствие 2. Вписанный угол, опирающийся на полуокружность – прямой.

M
N
F
О
А
С
В

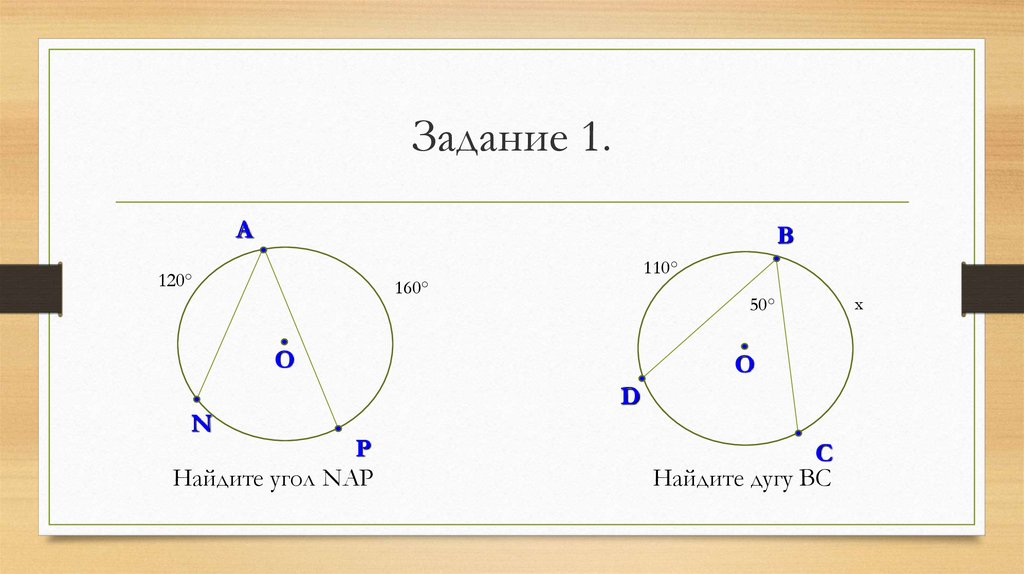
17. Задание 1.

А
В
120°
110°
160°
50°
О
N
P
Найдите угол NAP
О
D
С
Найдите дугу ВС
x

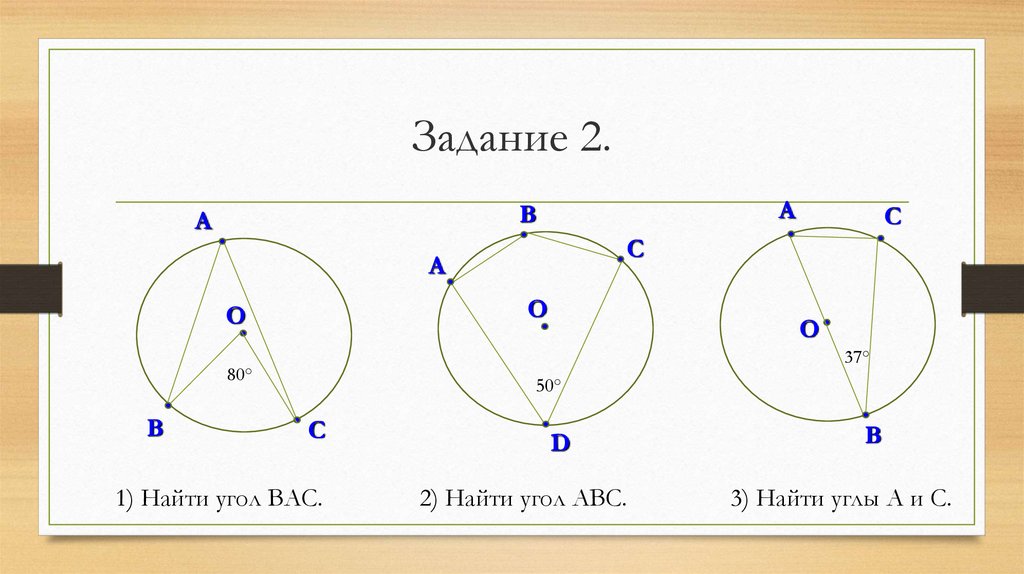
18. Задание 2.

А
B
А
C
А
О
О
О
37°
80°
B
C
50°
C
1) Найти угол ВАС.
D
2) Найти угол АВС.
B
3) Найти углы А и С.

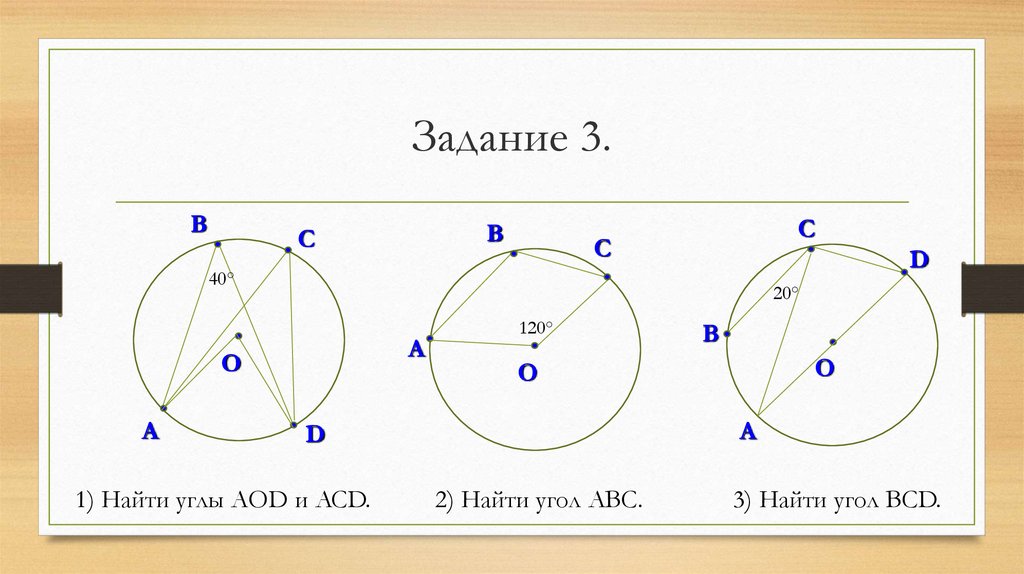
19. Задание 3.

B
B
C
C
C
D
40°
20°
A
О
A
120°
О
О
A
D
1) Найти углы АОD и ACD.
B
2) Найти угол АВС.
3) Найти угол ВСD.

20. Самостоятельная работа. Тестирование по материалам ОГЭ. Задание: Выберите верный вариант ответа

21. Домашнее задание. § 70 – 71, стр. 169 – 173. Выучить определения, теорему и следствия.

22. Подведем итоги.

С какими углами мы сегодня познакомились?
Что мы узнали о величине вписанного и центрального угла?
Какая связь между этими углами?
С какими свойствами вписанных углов мы познакомились?