Маркетинговые исследования. Дискриминантный анализ

1. Дискриминантный анализ

Курс «Маркетинговые исследования»

2. Сущность дискриминантного анализа

Дискриминантный анализ является
статистическим методом, который позволяет
изучить различия между двумя и более
группами объектов по нескольким переменным
одновременно.
2

3. Цели дискриминантного анализа

построение модели, позволяющей классифицировать
индивидуумов или объекты по группам на основании
независимых переменных;
определение статистической значимости различий
между двумя и более группами (например, между
теми, кто потребляет или не потребляет данный
продукт);
проверка соответствия дискриминантного множества
расчетному, полученному по независимым
переменным. Дискриминантное множество – это база
для отнесения объектов и индивидуумов к какой-либо
определенной группе.
3

4. Общая модель дискриминантного анализа, называемая также дискриминантной функцией, имеет вид уравнения:

Z = b 1 X 1 + b2 X 2+
…+
b n X n , где
Z – дискриминантное множество;
– коэффициенты дискриминантной функции
(дискриминантные веса);
X 1 n – независимые переменные.
b
1 n
4

5. Для проведения дискриминантного анализа необходимо образовать две (или более) обучающие выборки Z 1 и Z 2 объемами n 1 и n 2

соответственно.
Z 1 = ( a1 X i1 + a 2 X
i = 1 n
i2
+ a 3 X i3 + … + a n X in )
Среднее значение множества рассчитывается по формуле :
U Z 1 = 1/n 1 ( a 1 X i 1 + a 2 X
i2
+ a 3 X i3 + … + a n X in )
Аналогичные расчеты проводятся для выборки Z 2 :
Z 2= ( b1 X i1 + b 2 X
i2
+ b 3 X i3 + … + b n X in )
U Z 2 = 1/ n 2 ( b 1 X i 1 + b 2 X
i2
+ b 3 X i3 + … + b n X in )
Далее, находят константу дискриминации С по формуле:
С = ½ (U Z 1 + U Z 2 )
Если Z j C , то Z j следует отнести к совокупности Z 1; если Z j С , то Z j
5
относится к совокупности Z 2 .

6. Основные показатели различий между группами

Мерой различий между классами по нескольким
дискриминантным переменным может служить - статистика
Уилкса . Величины , близкие к нулю, говорят о высокой степени
различии между классами (т.е. центроиды классов сильно
отличаются друг от друга). Увеличение до ее максимального
значения, равного 1, приводит к постепенному уменьшению
различий, а центроиды классов приближаются друг к другу.
Необходимую точность вычислений обеспечивает тест
толерантности. Если проверяемая переменная является
линейной комбинацией (или приблизительно равна линейной
комбинации) одной или нескольких отобранных переменных, то ее
толерантность равна нулю (или близка к нулю). Такую
переменную нежелательно использовать в расчетах, потому что
она не дает никакой новой информации, но создает
вычислительные проблемы. Толерантность еще не отобранной
переменной равна единице минус квадрат множественной
корреляции между этой переменной и всеми уже отобранными
6
переменными.

7. Пример

Менеджер ресторана «Элис» хотел бы изучит вопрос
о рыночной сегментации для выявления
специфических характеристик, которые позволят
определить потенциальных посетителей ресторана.
Для решения этого вопроса менеджер обратился в
консультационную фирму с просьбой провести анализ.
Исследование, проведенное с помощью фокус- группы,
показало, что посетители различных ресторанов
различаются по некоторым социальнодемографическим показателям ( возраст, доход,
семейное положение ), а также по требованиям,
предъявляемым к качеству и разнообразию блюд,
обслуживанию и т.п. Однако, для выявления факторов,
оказывающих влияние на предпочтения посетителей
ресторанов, было решено использовать
7
дискриминантный анализ.

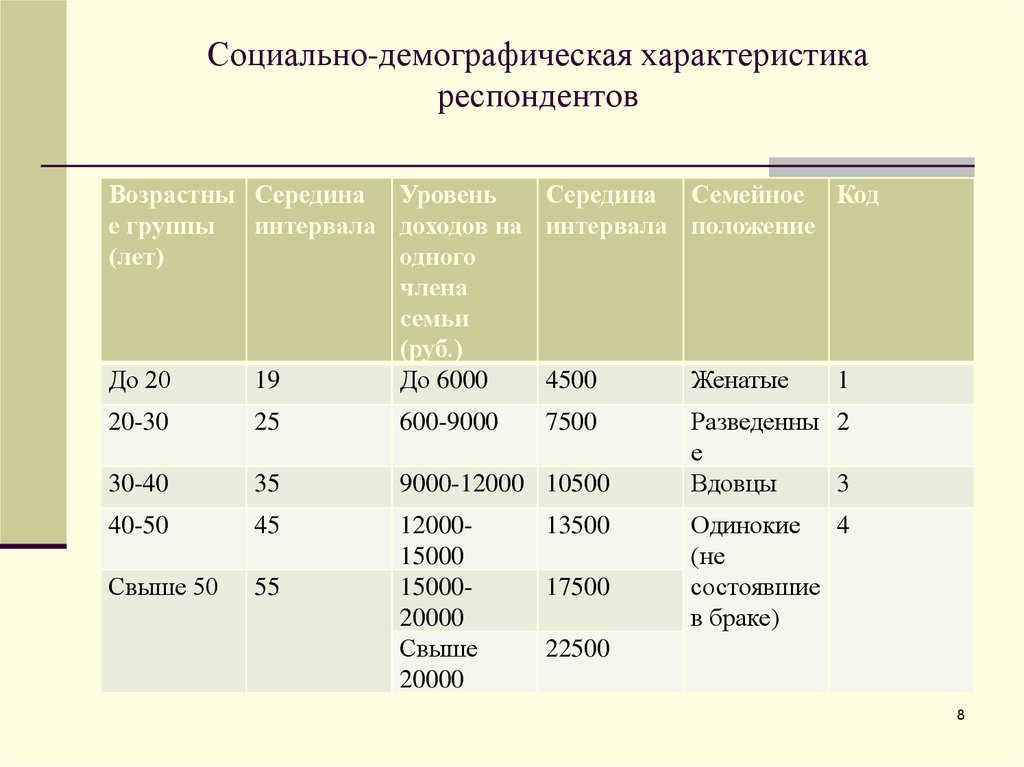
8. Социально-демографическая характеристика респондентов

Возрастны Середина Уровень
Середина Семейное Код
е группы
интервала доходов на интервала положение
(лет)
одного
члена
семьи
(руб.)
До 20
19
До 6000
4500
Женатые
1
20-30
25
600-9000
7500
30-40
35
9000-12000 10500
40-50
45
Свыше 50
55
1200015000
1500020000
Свыше
20000
13500
17500
Разведенны 2
е
Вдовцы
3
Одинокие 4
(не
состоявшие
в браке)
22500
8

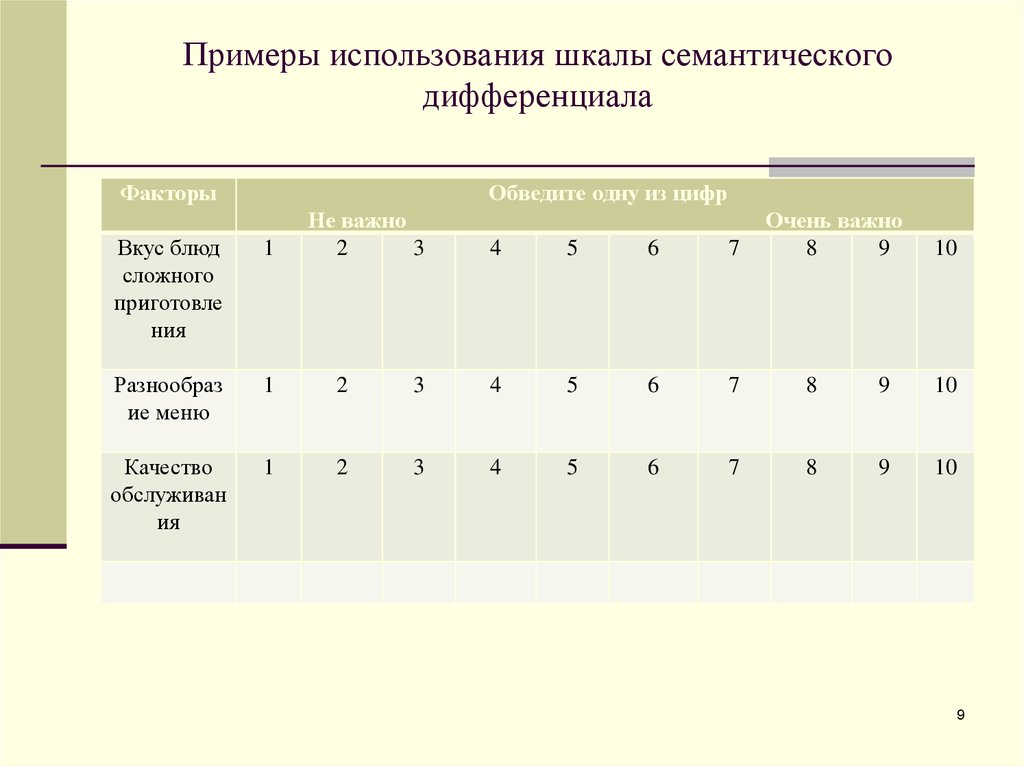
9. Примеры использования шкалы семантического дифференциала

Факторы
Обведите одну из цифр
Не важно
2
3
Вкус блюд
сложного
приготовле
ния
1
Разнообраз
ие меню
1
2
Качество
обслуживан
ия
1
2
Очень важно
8
9
4
5
6
7
10
3
4
5
6
7
8
9
10
3
4
5
6
7
8
9
10
9

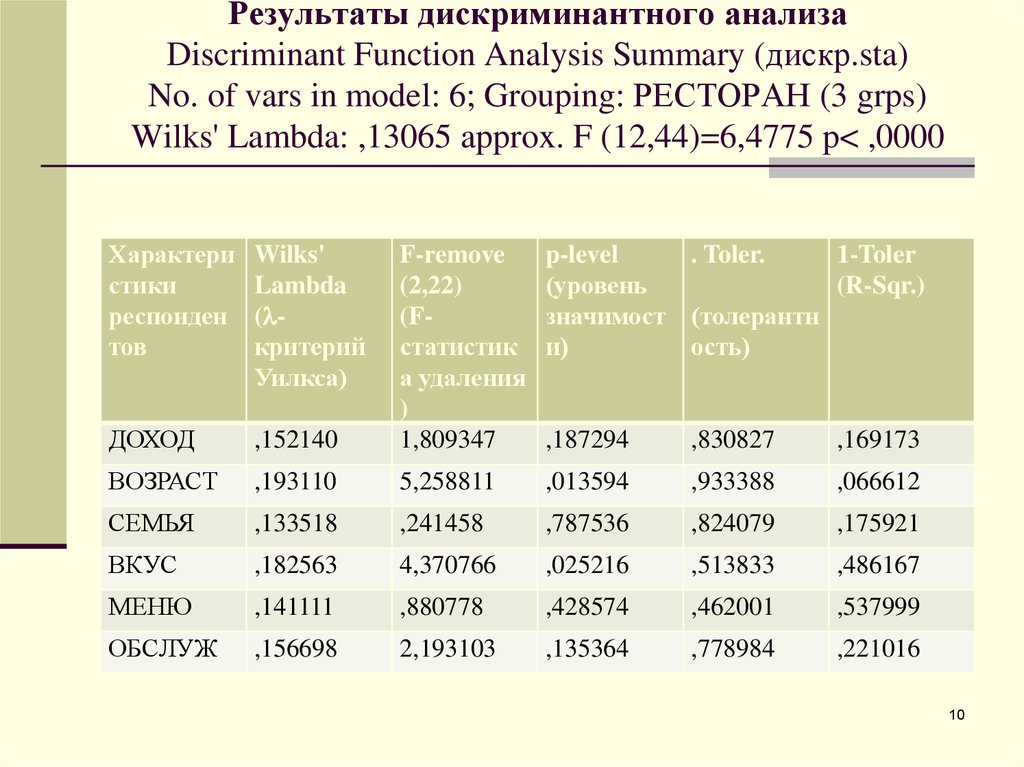
10. Результаты дискриминантного анализа Discriminant Function Analysis Summary (дискр.sta) No. of vars in model: 6; Grouping:

РЕСТОРАН (3 grps)
Wilks' Lambda: ,13065 approx. F (12,44)=6,4775 p< ,0000
Характери
стики
респонден
тов
Wilks'
Lambda
( критерий
Уилкса)
ДОХОД
p-level
. Toler.
1-Toler
(уровень
(R-Sqr.)
значимост (толерантн
и)
ость)
,152140
F-remove
(2,22)
(Fстатистик
а удаления
)
1,809347
,187294
,830827
,169173
ВОЗРАСТ
,193110
5,258811
,013594
,933388
,066612
СЕМЬЯ
,133518
,241458
,787536
,824079
,175921
ВКУС
,182563
4,370766
,025216
,513833
,486167
МЕНЮ
,141111
,880778
,428574
,462001
,537999
ОБСЛУЖ
,156698
2,193103
,135364
,778984
,221016
10

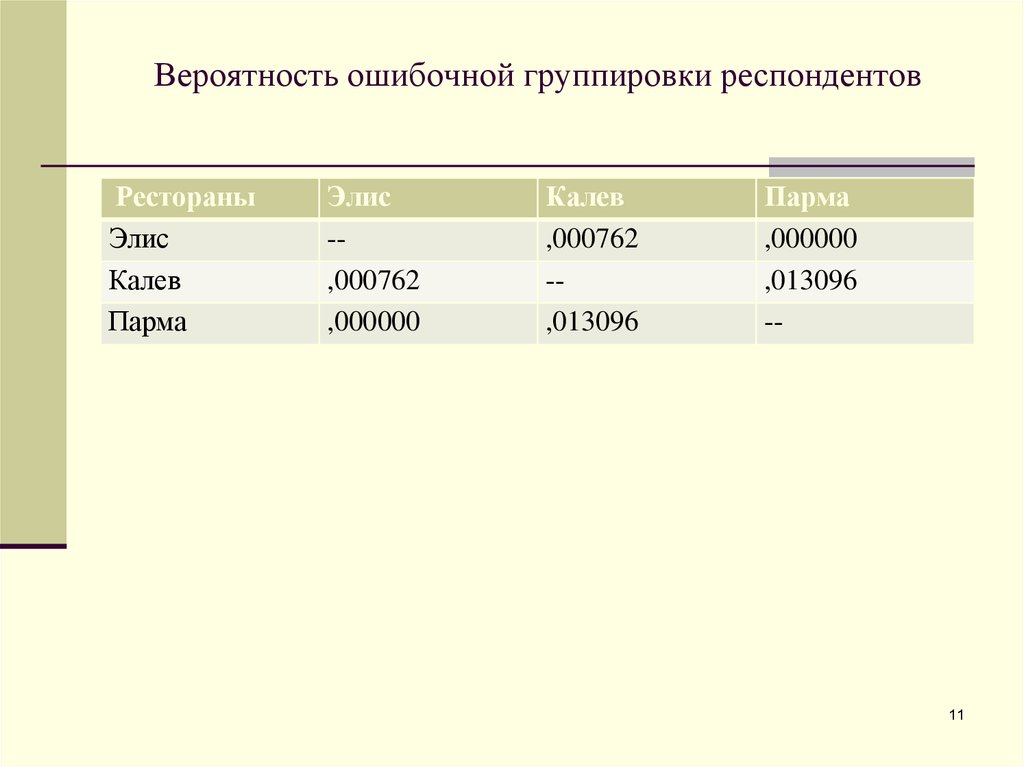
11. Вероятность ошибочной группировки респондентов

Рестораны
Элис
Калев
Парма
Элис
-,000762
,000000
Калев
,000762
-,013096
Парма
,000000
,013096
--
11

12. File IRISDAT

SEPALLEN
SEPALWID
PETALLEN
PETALWID
IRISTYPE
Length of Sepals – длина чашелистиков
Width of Sepals – ширина чашелистиков
Length of Petals – длина лепестков
Width of Petals – ширина лепестков
Three types of iris – три типа ириса
12

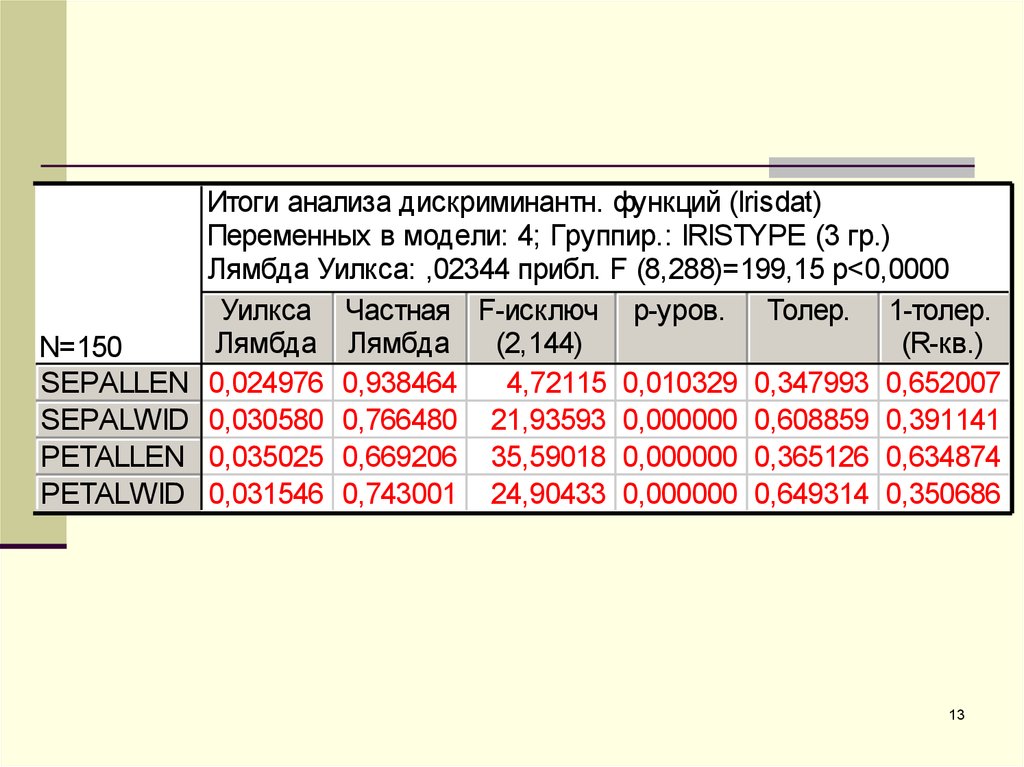
13.

N=150
SEPALLEN
SEPALWID
PETALLEN
PETALWID
Итоги анализа дискриминантн. функций (Irisdat)
Переменных в модели: 4; Группир.: IRISTYPE (3 гр.)
Лямбда Уилкса: ,02344 прибл. F (8,288)=199,15 p<0,0000
Уилкса Частная F-исключ p-уров. Толер. 1-толер.
Лямбда Лямбда
(2,144)
(R-кв.)
0,024976 0,938464
4,72115 0,010329 0,347993 0,652007
0,030580 0,766480 21,93593 0,000000 0,608859 0,391141
0,035025 0,669206 35,59018 0,000000 0,365126 0,634874
0,031546 0,743001 24,90433 0,000000 0,649314 0,350686
13

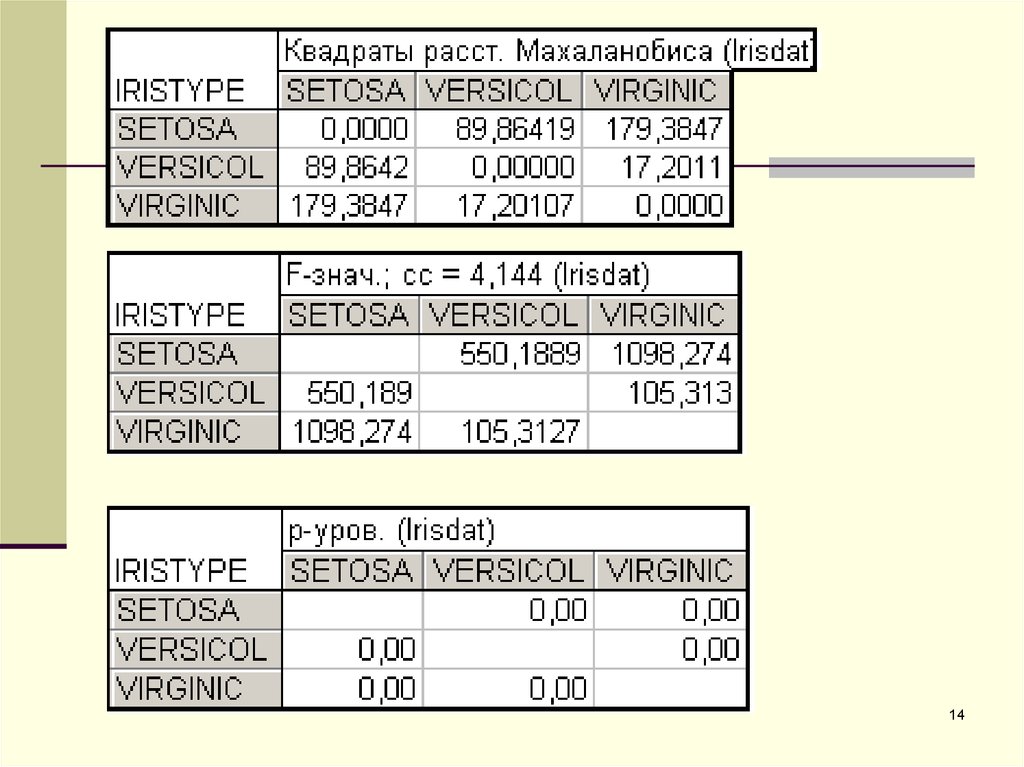
14.

14

15.

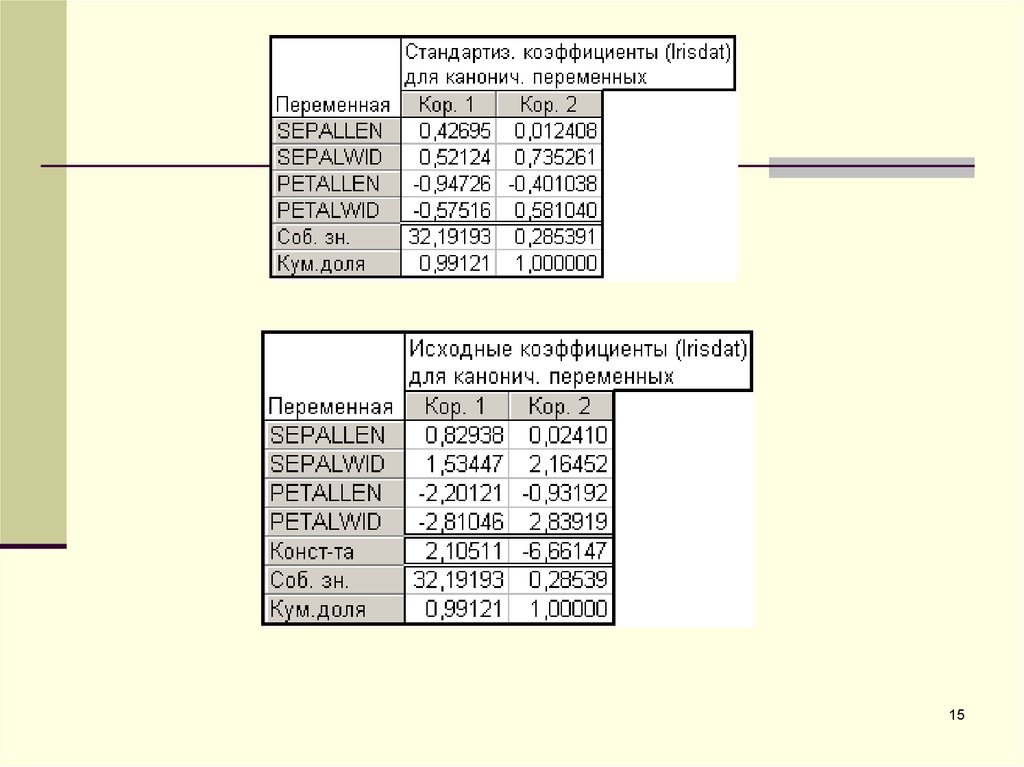
15

16.

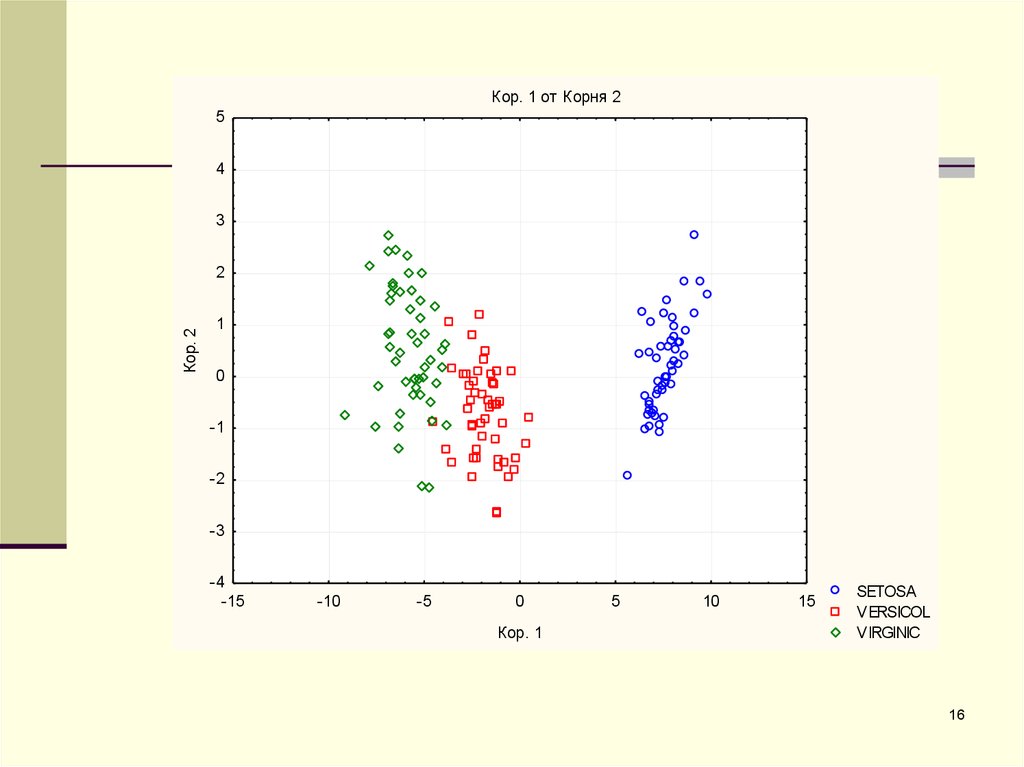
Кор. 1 от Корня 2
5
4
3
Кор. 2
2
1
0
-1
-2
-3
-4
-15
-10
-5
0
Кор. 1
5
10
15
SETOSA
VERSICOL
VIRGINIC
16

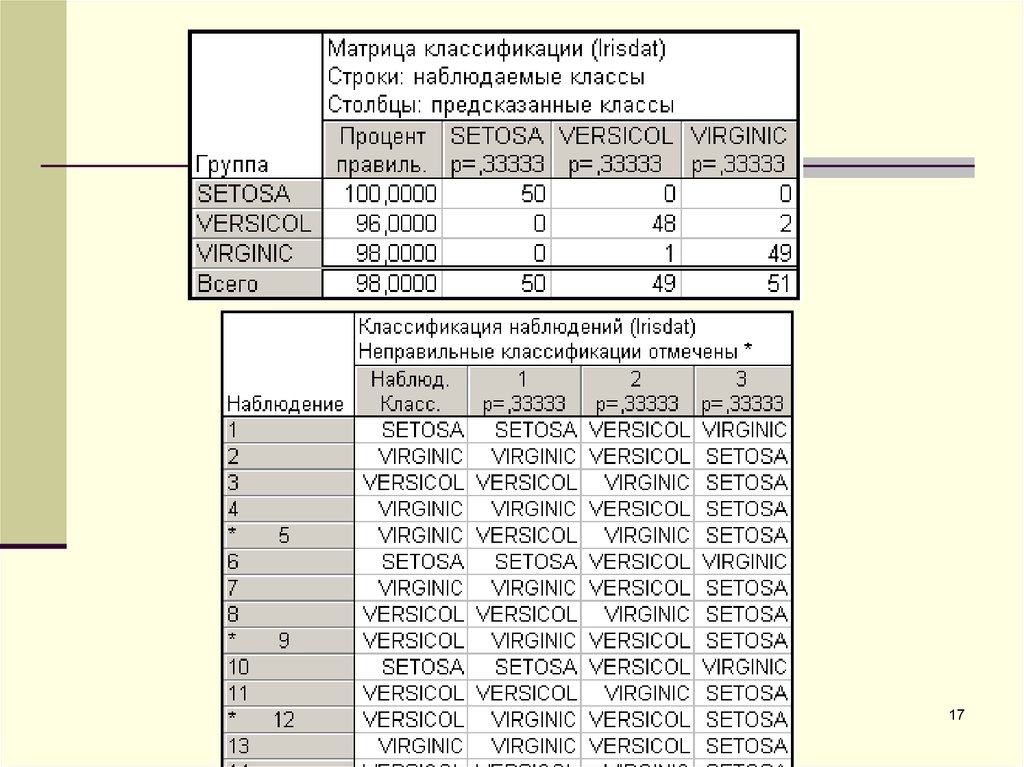
17.

17

18.

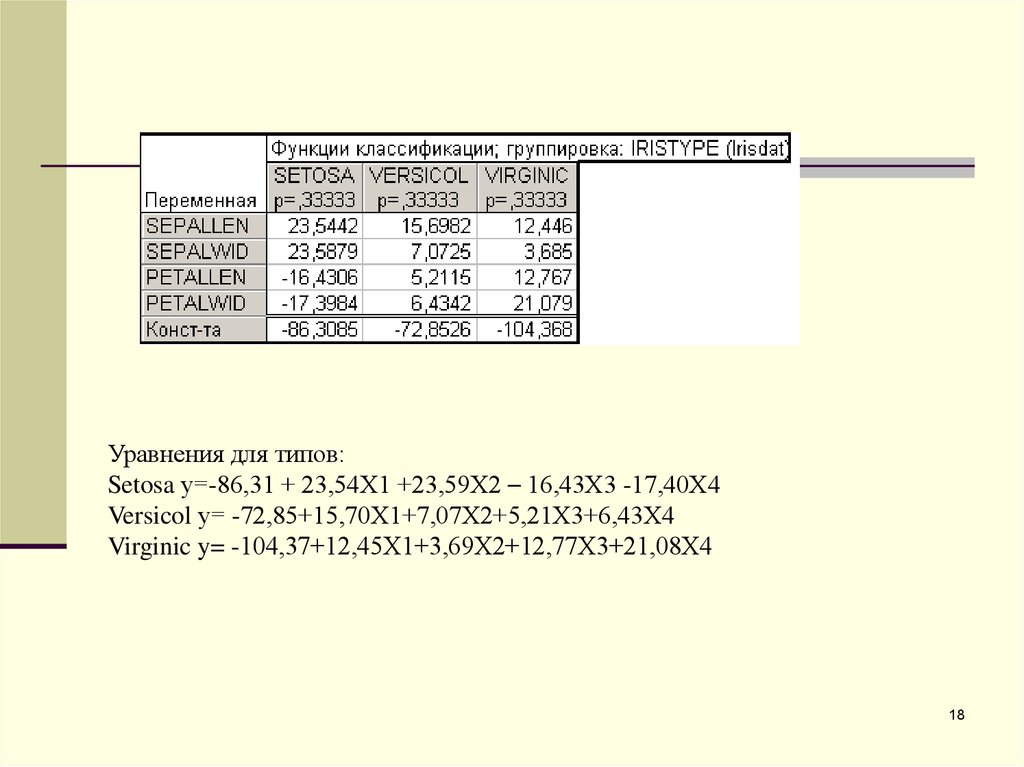
Уравнения для типов:
Setosa у=-86,31 + 23,54Х1 +23,59Х2 – 16,43Х3 -17,40Х4
Versicol у= -72,85+15,70Х1+7,07Х2+5,21Х3+6,43Х4
Virginic y= -104,37+12,45Х1+3,69Х2+12,77Х3+21,08Х4
18