Точность расчетной модели

1.

Точность расчетной модели
Два полезных результата:
e 0
X e
i i
0
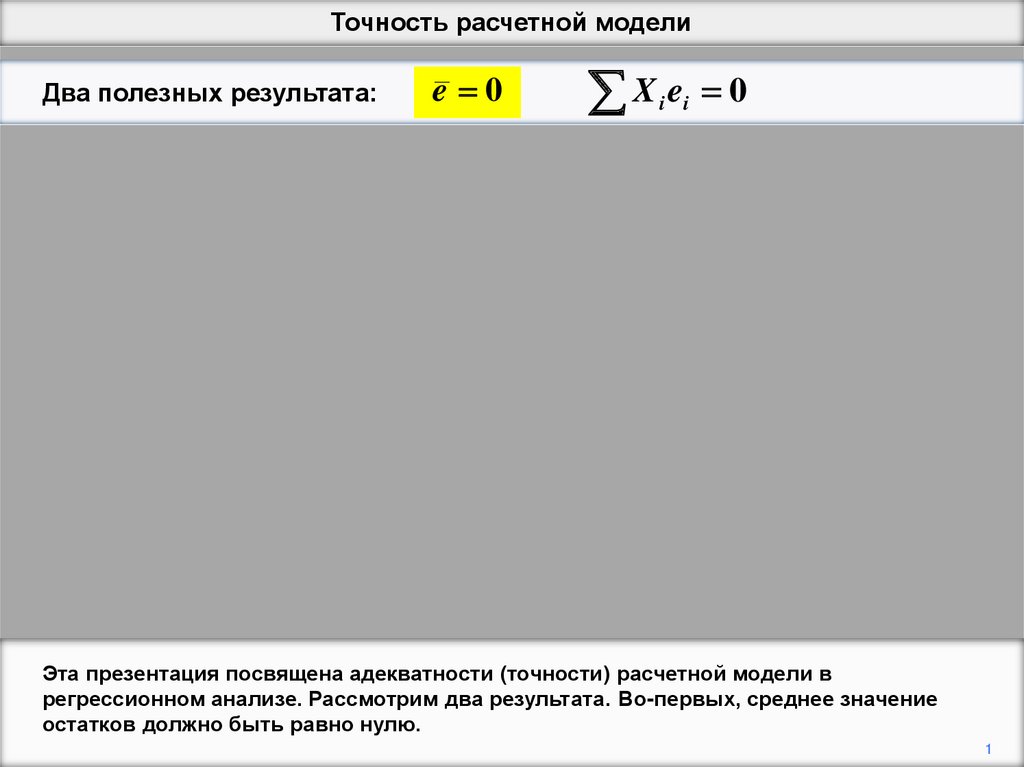
Эта презентация посвящена адекватности (точности) расчетной модели в
регрессионном анализе. Рассмотрим два результата. Во-первых, среднее значение
остатков должно быть равно нулю.
1

2.

Точность расчетной модели
Два полезных результата:
e 0
X e
i i
0
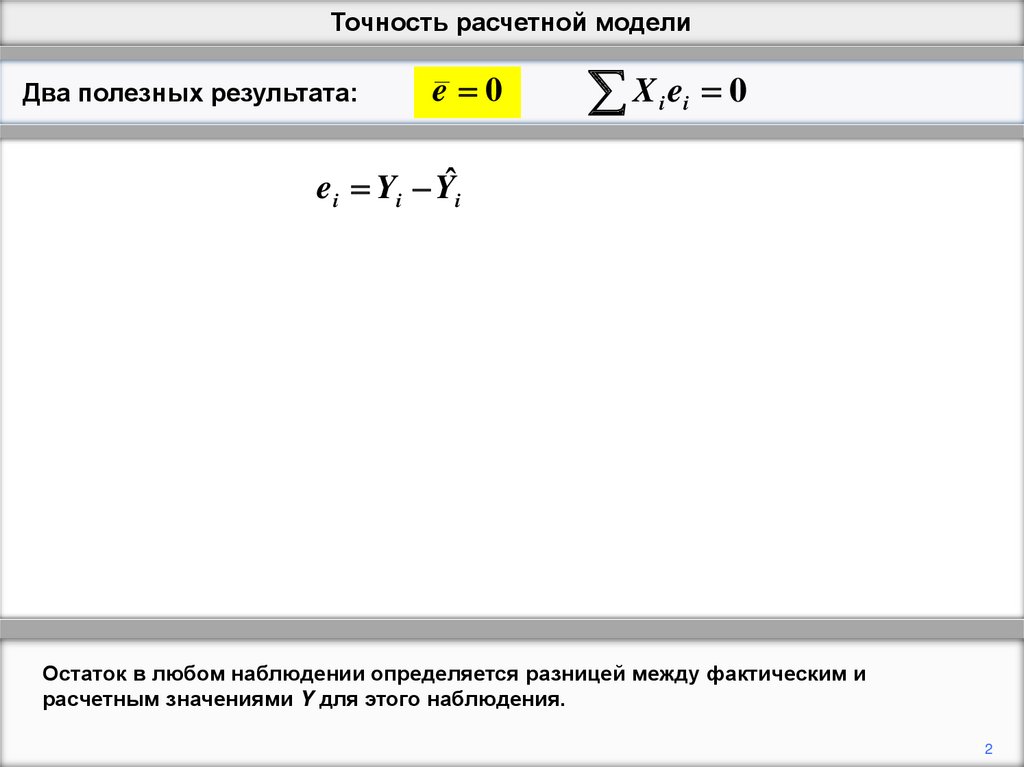
ei Yi Yˆi Yi b1 b2 X i
Остаток в любом наблюдении определяется разницей между фактическим и
расчетным значениями Y для этого наблюдения.
2

3.

Точность расчетной модели
Два полезных результата:
e 0
X e
i i
ei Yi Yˆi Yi b1 b2 X i
0
Yˆi b1 b2 X i
Вначале заменим расчетное значение выражением для него.
3

4.

Точность расчетной модели
Два полезных результата:
e 0
X e
i i
0
ei Yi Yˆi Yi b1 b2 X i
e Y
i
i
nb1 b2 X i
Просуммируем все наблюдения.
4

5.

Точность расчетной модели
Два полезных результата:
e 0
X e
i i
0
ei Yi Yˆi Yi b1 b2 X i
e Y
i
i
nb1 b2 X i
1
1
1
e
Y
b
b
Xi
i
i
1
2
n
n
n
e Y b1 b2 X
Y Y b2 X b2 X
0
Разделив на n, мы получим среднее значение остатков, выраженное через значения X,
Y и коэффициенты регрессии.
5

6.

Точность расчетной модели
Два полезных результата:
e 0
X e
i i
0
ei Yi Yˆi Yi b1 b2 X i
e Y
i
i
nb1 b2 X i
1
1
1
e
Y
b
b
Xi
i
i
1
2
n
n
n
e Y b1 b2 X
b1 Y b2 X
Y Y b2 X b2 X
0
Если мы заменим b1, выражение будет равно нулю.
6

7.

Точность расчетной модели
Два полезных результата:
e 0
X e
i i
0
e 0
1
e ei
n
e
i
0
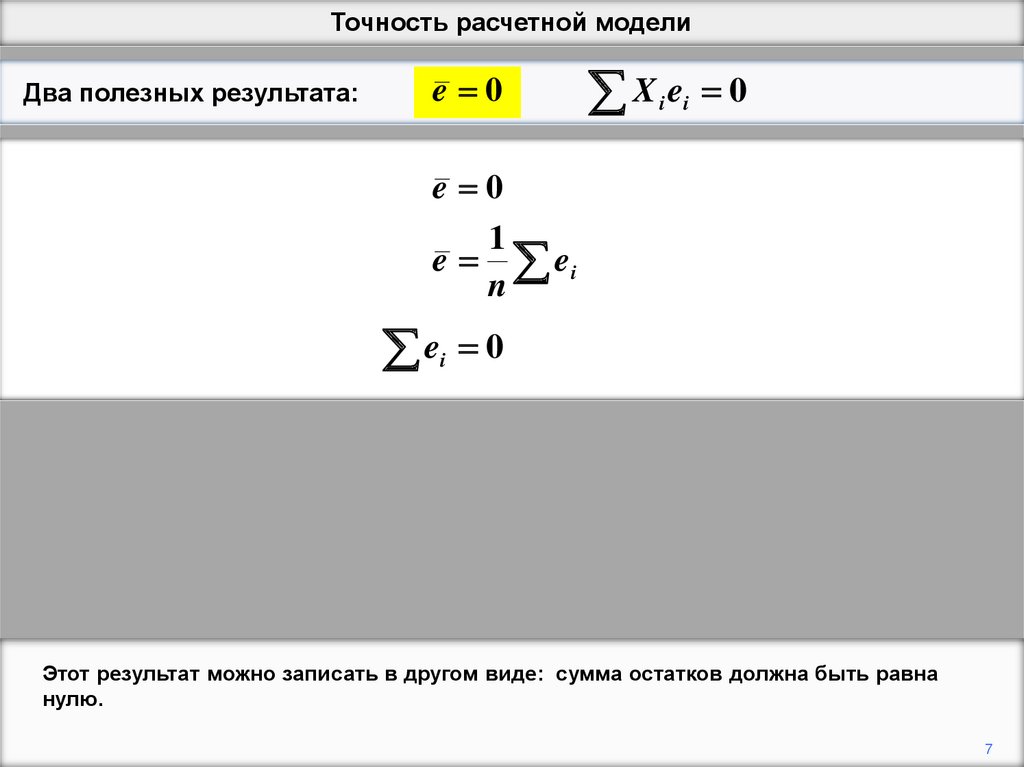
Этот результат можно записать в другом виде: сумма остатков должна быть равна
нулю.
7

8.

Точность расчетной модели
Два полезных результата:
e 0
Дальнейшие результаты:
Yˆ Y
X e
i i
0
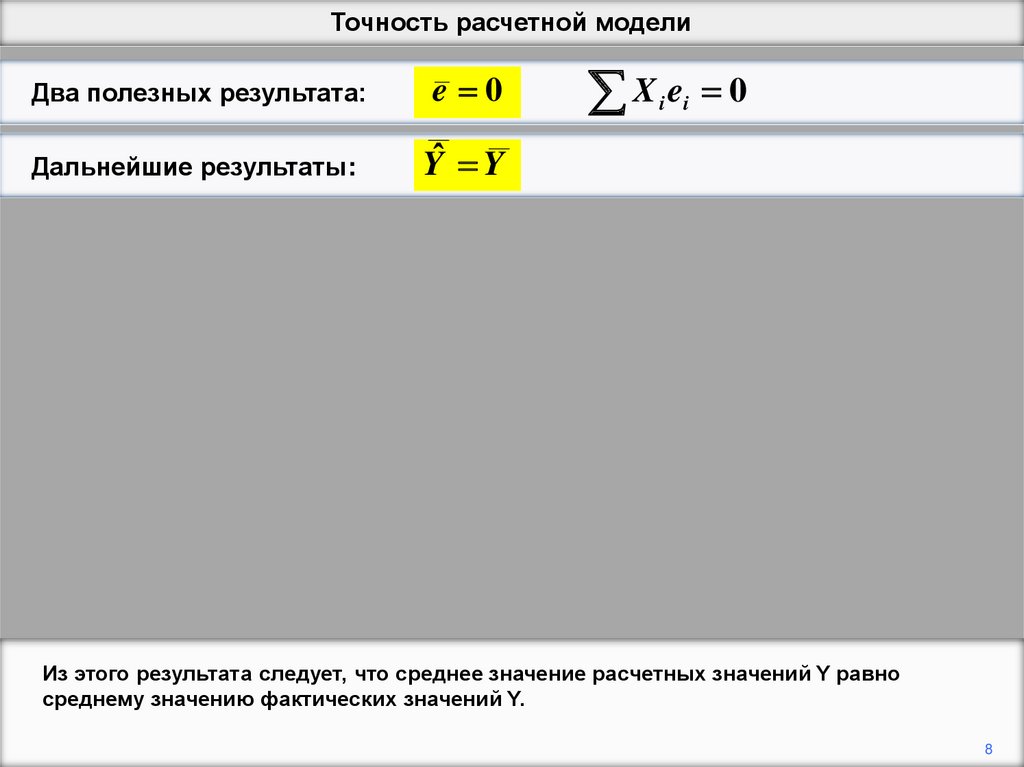
Из этого результата следует, что среднее значение расчетных значений Y равно
среднему значению фактических значений Y.
8

9.

Точность расчетной модели
Два полезных результата:
Дальнейшие результаты:
e 0
X e
i i
0
Yˆ Y
ei Yi Yˆi
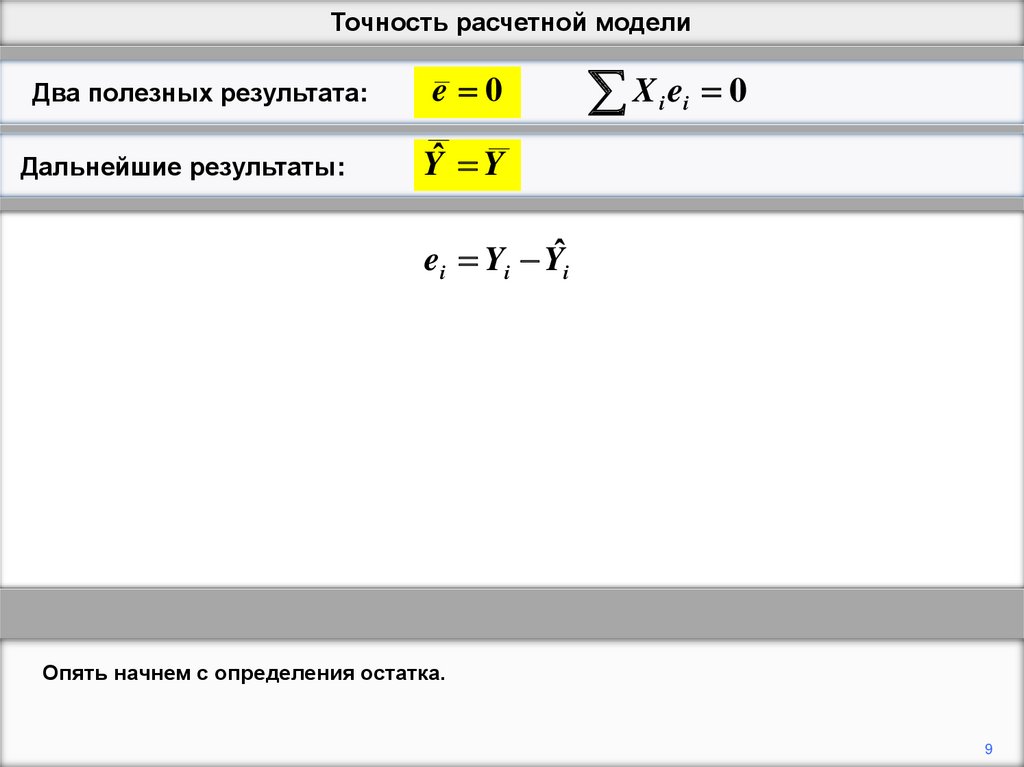
Опять начнем с определения остатка.
9

10.

Точность расчетной модели
Два полезных результата:
e 0
Дальнейшие результаты:
Yˆ Y
X e
i i
0
ei Yi Yˆi
e Y Yˆ
i
i
i
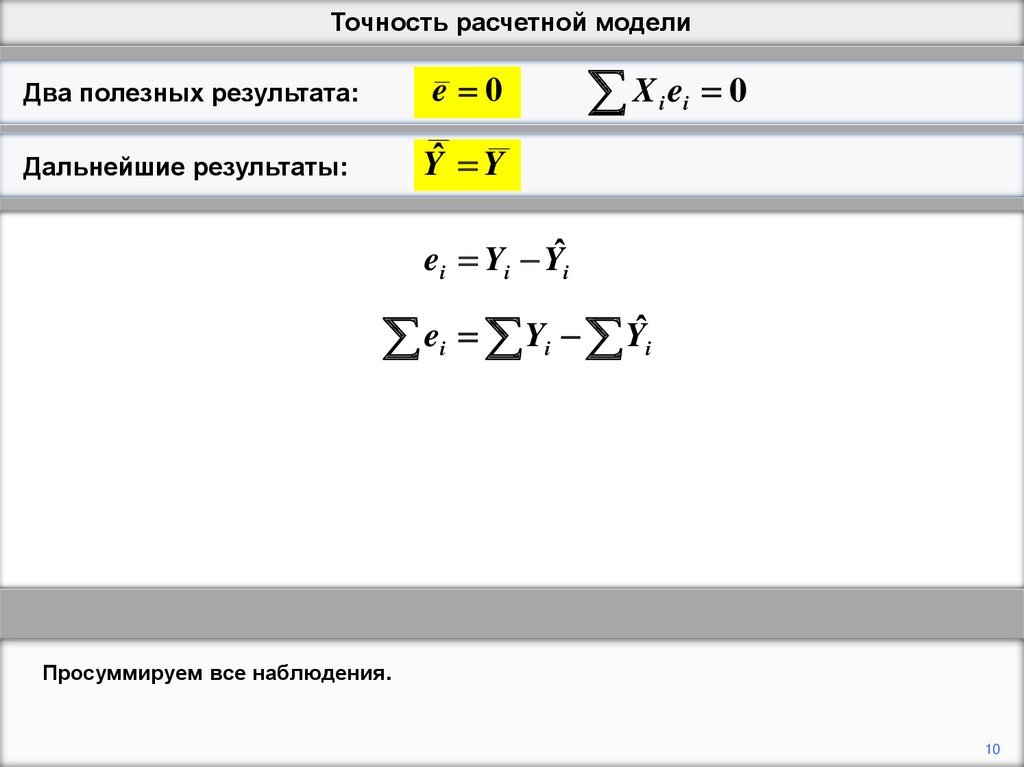
Просуммируем все наблюдения.
10

11.

Точность расчетной модели
Два полезных результата:
e 0
Дальнейшие результаты:
Yˆ Y
X e
i i
0
ei Yi Yˆi
e Y Yˆ
i
i
i
1
1
0 Yi Yˆi Y Yˆ
n
n
В левой части сумма остатков равна нулю. Теперь выражение разделим на n.
11

12.

Точность расчетной модели
Два полезных результата:
e 0
Дальнейшие результаты:
Yˆ Y
X e
i i
0
ei Yi Yˆi
e Y Yˆ
i
i
i
1
1
0 Yi Yˆi Y Yˆ
n
n
Yˆ Y
Следовательно, среднее значение расчетных значений равно среднему значению
фактических значений.
12

13.

Точность расчетной модели
Два полезных результата:
e 0
Дальнейшие результаты:
Yˆ Y
X e
i i
0
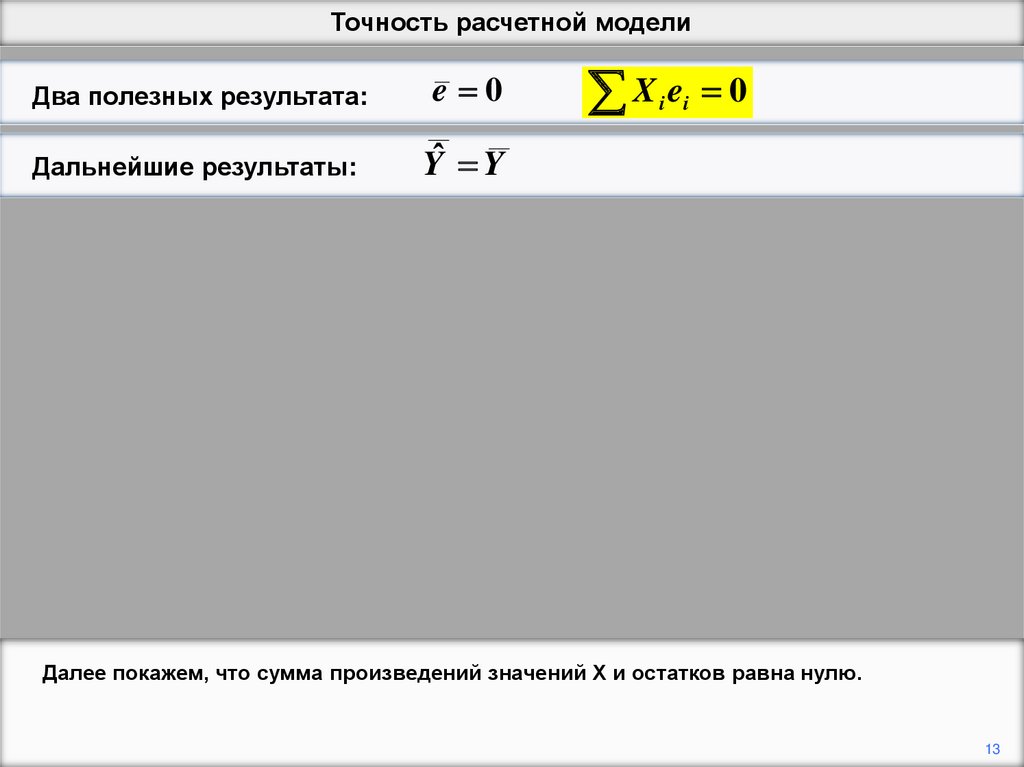
Далее покажем, что сумма произведений значений X и остатков равна нулю.
13

14.

Точность расчетной модели
Два полезных результата:
e 0
Дальнейшие результаты:
Yˆ Y
X e
i i
X e X Y b b X
X Y b X b X
i i
i
i
i
i
1
1
2
0
i
i
2
2
i
0
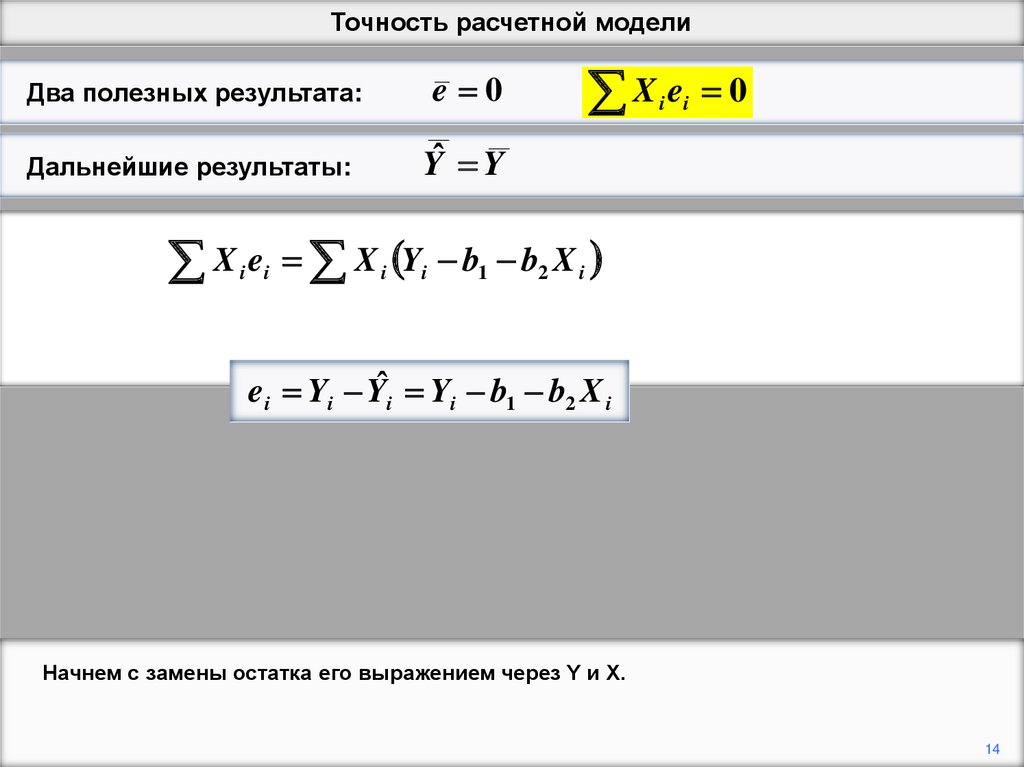
ei Yi Yˆi Yi b1 b2 X i
Начнем с замены остатка его выражением через Y и X.
14

15.

Точность расчетной модели
Два полезных результата:
e 0
Дальнейшие результаты:
Yˆ Y
X e
i i
X e X Y b b X
X Y b X b X
i i
i
i
i
i
1
1
2
0
i
i
2
2
i
0
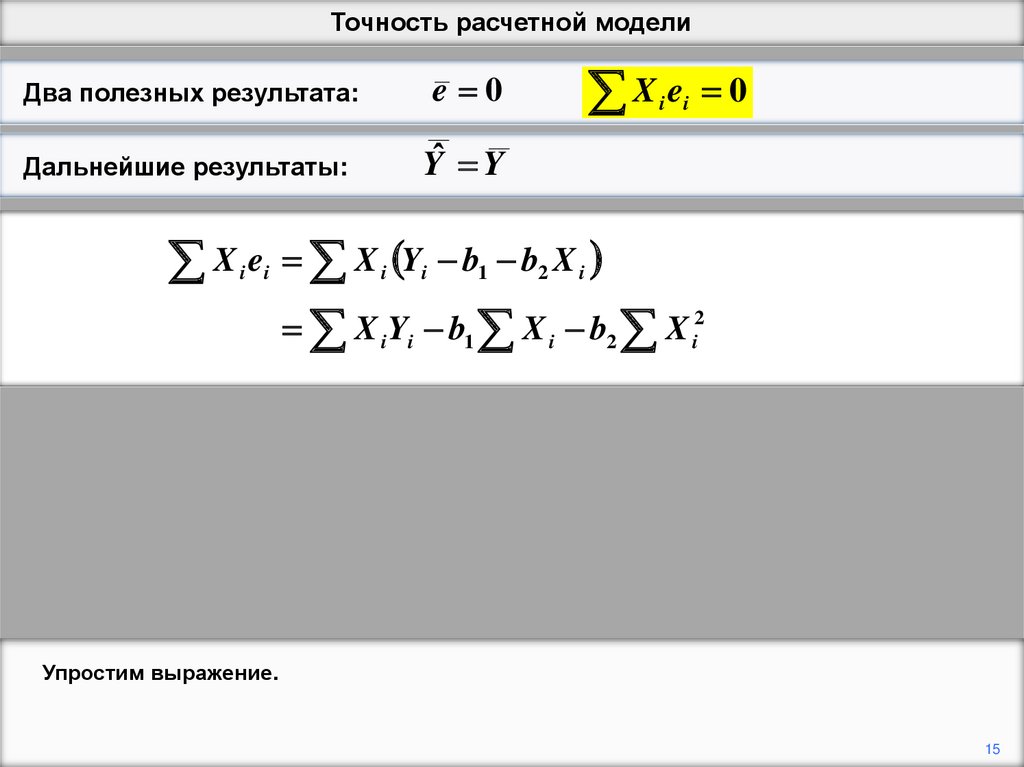
Упростим выражение.
15

16.

Точность расчетной модели
Два полезных результата:
e 0
Дальнейшие результаты:
Yˆ Y
X e
i i
X e X Y b b X
X Y b X b X
i i
i
i
i
i
1
1
2
0
i
i
2
2
i
0
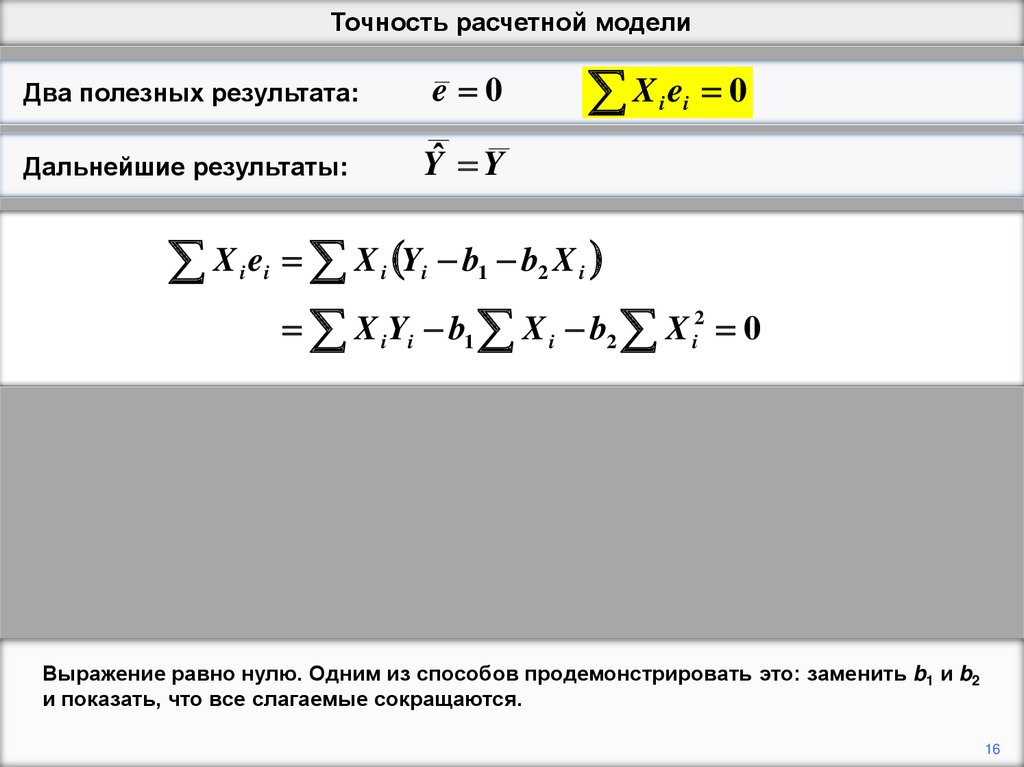
Выражение равно нулю. Одним из способов продемонстрировать это: заменить b1 и b2
и показать, что все слагаемые сокращаются.
16

17.

Точность расчетной модели
Два полезных результата:
e 0
Дальнейшие результаты:
Yˆ Y
X e
i i
X e X Y b b X
X Y b X b X
i i
i
i
i
i
1
1
2
0
i
i
2
2
i
0
RSS
0 2b2 X i2 2 X iYi 2b1 X i 0
b2
Точный способ - вспомнить условие первого порядка для b2 при выводе
коэффициентов регрессии. Вы можете видеть, что так оно и есть.
17

18.

Точность расчетной модели
Два полезных результата:
e 0
Дальнейшие результаты:
Yˆ Y
X e
Yˆ e
i i
0
i i
0
Наконец, побочным результатом нашего последнего расчета, является равенство
нулю суммы произведений расчетных значений Y и остатков.
18

19.

Точность расчетной модели
Два полезных результата:
e 0
Дальнейшие результаты:
Yˆ Y
X e
Yˆ e
i i
0
i i
0
Yˆ
Yˆ e b b X e
b e b X e
b ne b X e 0
i i
1
2
1 i
1
i
2
2
i
i
b1 b2 X i
i i
i i
Сначала подставим расчетные значения Y.
19

20.

Точность расчетной модели
Два полезных результата:
e 0
Дальнейшие результаты:
Yˆ Y
X e
Yˆ e
i i
0
i i
0
Yˆ e b b X e
b e b X e
b ne b X e 0
i i
1
2
1 i
1
e
i
i
i
2
2
i i
i i
ne
Производим расчеты.
20

21.

Точность расчетной модели
Два полезных результата:
e 0
Дальнейшие результаты:
Yˆ Y
X e
Yˆ e
i i
0
i i
0
Yˆ e b b X e
b e b X e
b ne b X e 0
i i
1
2
1 i
1
e 0
i
i
2
2
i i
i i
X e
i i
0
Выражение равно нулю, учитывая ранее полученные результаты.
21

22.

Точность расчетной модели
Y
i
Y
2
Yˆ Y e
Yˆ Y e
Yˆ Y e
2
ˆ
Yi ei Y
2
i
i
2
i
2 Yˆi Y ei
2
2
i
2 Yˆi ei 2Y ei
i
i
2
Мерой вариации Y является сумма его квадратов отклонений от среднего значения
выборки. Это называется общей суммой квадратов TSS.
22

23.

Точность расчетной модели
Y
i
Y
2
ˆ Y e
Y
Y Yˆ Y Yˆ e
Yˆ Y e 2 Yˆ Y e
Yˆ Y e 2 Yˆ e 2Y e
2
ˆ
Yi ei Y
2
ei
i
i
i
i
i
2
i
2
i
i
i
2
i
i
2
i
i i
i
i
Мы разложим общую сумму квадратов, используя тот факт, что фактическое значение
Y в любом наблюдении равно сумме его расчетного значения и остатка.
23

24.

Точность расчетной модели
Y
i
Y
2
ˆ Y e
Y
Y Yˆ Y Yˆ e
Yˆ Y e 2 Yˆ Y e
Yˆ Y e 2 Yˆ e 2Y e
2
ˆ
Yi ei Y
2
ei
i
i
i
i
i
2
i
2
i
i
i
2
i
i
2
i
i i
i
i
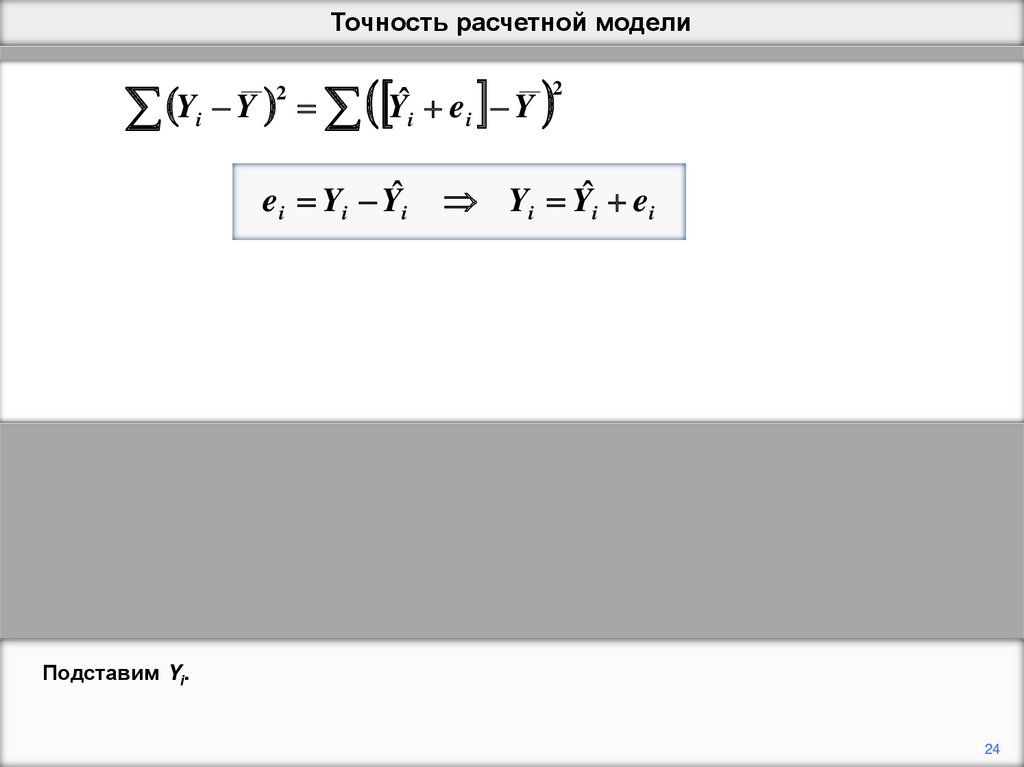
Подставим Yi.
24

25.

Точность расчетной модели
Y
i
Y
2
Yˆ Y e
Yˆ Y e
Yˆ Y e
2
ˆ
Yi ei Y
2
i
i
2
i
2 Yˆi Y ei
2
2
i
2 Yˆi ei 2Y ei
i
i
2
Перегруппируем члены.
25

26.

Точность расчетной модели
Y
i
Y
2
Yˆ Y e
Yˆ Y e
Yˆ Y e
2
ˆ
Yi ei Y
2
i
i
2
2
i
2 Yˆi Y ei
2
2
i
2 Yˆi ei 2Y ei
i
i
Разложим квадрат в правой части уравнения.
26

27.

Точность расчетной модели
Y
i
Y
2
Yˆ Y e
Yˆ Y e
Yˆ Y e
2
ˆ
Yi ei Y
2
i
i
2
i
2 Yˆi Y ei
2
2
i
2 Yˆi ei 2Y ei
i
i
2
Разложим третий член в правой части уравнения.
27

28.

Точность расчетной модели
Y
i
Y
2
Yˆ Y e
Yˆ Y e
Yˆ Y e
2
ˆ
Yi ei Y
2
i
i
2
i
2 Yˆi Y ei
2
2
i
2 Yˆi ei 2Y ei
i
i
2
Yˆ e
i i
0
e
i
0
Последние два члена равны нулю, учитывая ранее полученные результаты.
28

29.

Точность расчетной модели
Y
i
Y
2
Yˆ Y e
Yˆ Y e
Yˆ Y e
2
ˆ
Yi ei Y
2
i
i
2
2
i
2 Yˆi Y ei
2
2
i
2 Yˆi ei 2Y ei
i
i
TSS ESS RSS
2
Y
Y
TSS, total sum of squares
i
2
ˆ
Yi Y ESS, explained sum of squares
2
e
i RSS, residual sum of squares
Мы показали, что TSS, общая сумма квадратов Y может быть разложена на ESS,
объяснённую сумму квадратов, и RSS, сумму квадратов остатков.
29

30.

Точность расчетной модели
Y
i
Y
2
Yˆ Y e
Yˆ Y e
Yˆ Y e
2
ˆ
Yi ei Y
2
i
i
2
2
i
2 Yˆi Y ei
2
2
i
2 Yˆi ei 2Y ei
i
i
TSS ESS RSS
2
Y
Y
TSS, total sum of squares
i
2
ˆ
Yi Y ESS, explained sum of squares
2
e
i RSS, residual sum of squares
Слова, «объясненные» и «необъяснимые», заключены в кавычки, потому что
объяснение может быть ложным. Y может действительно зависеть от некоторой
другой переменной Z, а X может выступать в качестве замены для Z.
30

31.

Точность расчетной модели
Y
i
Y
2
Yˆ Y e
Yˆ Y e
Yˆ Y e
2
ˆ
Yi ei Y
2
i
i
2
2
i
2 Yˆi Y ei
2
2
i
2 Yˆi ei 2Y ei
i
i
TSS ESS RSS
2
Y
Y
TSS, total sum of squares
i
2
ˆ
Yi Y ESS, explained sum of squares
2
e
i RSS, residual sum of squares
Правильнее, «явно объясненные» вместо «объясненные».
31

32.

Точность расчетной модели
Y
i
Y
2
2
ˆ
Yi Y ei2
TSS ESS RSS
2
ˆ
(
Y
Y
)
ESS
i
R2
TSS (Yi Y ) 2
Основным критерием точности расчетной модели является коэффициент
детерминации R2, определяемый как отношение ESS к TSS, то есть часть дисперсии Y,
объясняемая уравнением регрессии.
32

33.

Точность расчетной модели
. reg EARNINGS S
Source |
SS
df
MS
-------------+-----------------------------Model | 19321.5589
1 19321.5589
Residual | 92688.6722
538 172.283777
-------------+-----------------------------Total | 112010.231
539 207.811189
Number of obs
F( 1,
538)
Prob > F
R-squared
Adj R-squared
Root MSE
=
=
=
=
=
=
540
112.15
0.0000
0.1725
0.1710
13.126
-----------------------------------------------------------------------------EARNINGS |
Coef.
Std. Err.
t
P>|t|
[95% Conf. Interval]
-------------+---------------------------------------------------------------S |
2.455321
.2318512
10.59
0.000
1.999876
2.910765
_cons | -13.93347
3.219851
-4.33
0.000
-20.25849
-7.608444
------------------------------------------------------------------------------
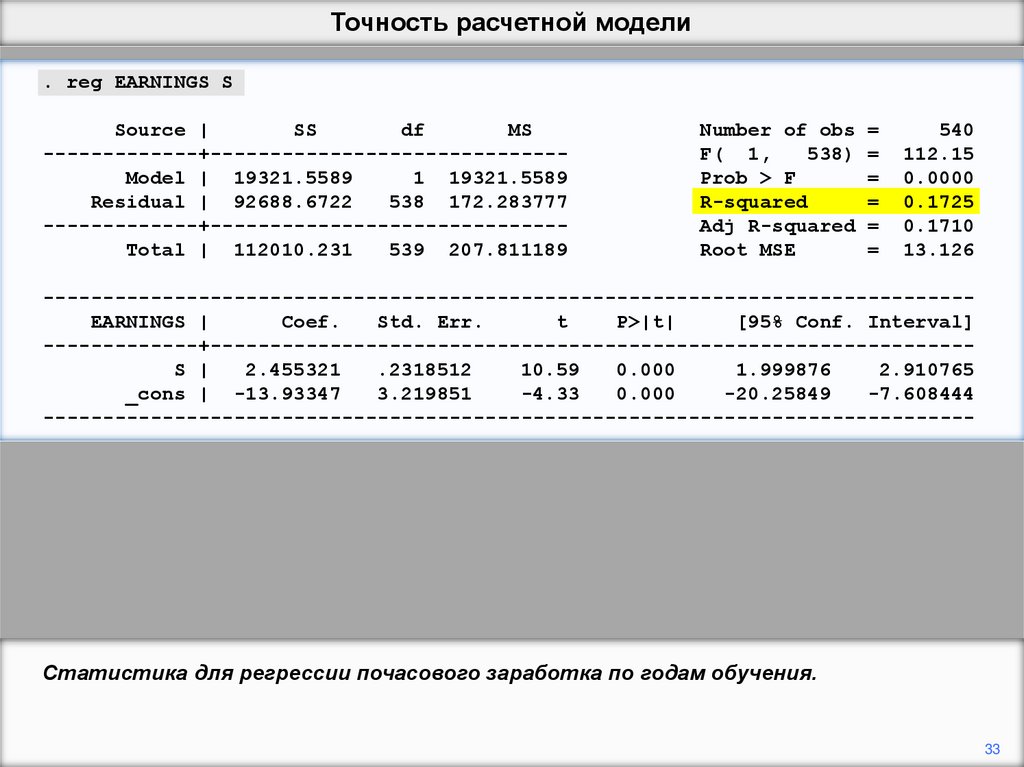
Статистика для регрессии почасового заработка по годам обучения.
33

34.

Точность расчетной модели
. reg EARNINGS S
Source |
SS
df
MS
-------------+-----------------------------Model | 19321.5589
1 19321.5589
Residual | 92688.6722
538 172.283777
-------------+-----------------------------Total | 112010.231
539 207.811189
Number of obs
F( 1,
538)
Prob > F
R-squared
Adj R-squared
Root MSE
=
=
=
=
=
=
540
112.15
0.0000
0.1725
0.1710
13.126
-----------------------------------------------------------------------------EARNINGS |
Coef.
Std. Err.
t
P>|t|
[95% Conf. Interval]
-------------+---------------------------------------------------------------S |
2.455321
.2318512
10.59
0.000
1.999876
2.910765
_cons | -13.93347
3.219851
-4.33
0.000
-20.25849
-7.608444
------------------------------------------------------------------------------
ESS 19,322
R
0.1725
TSS 112,010
2
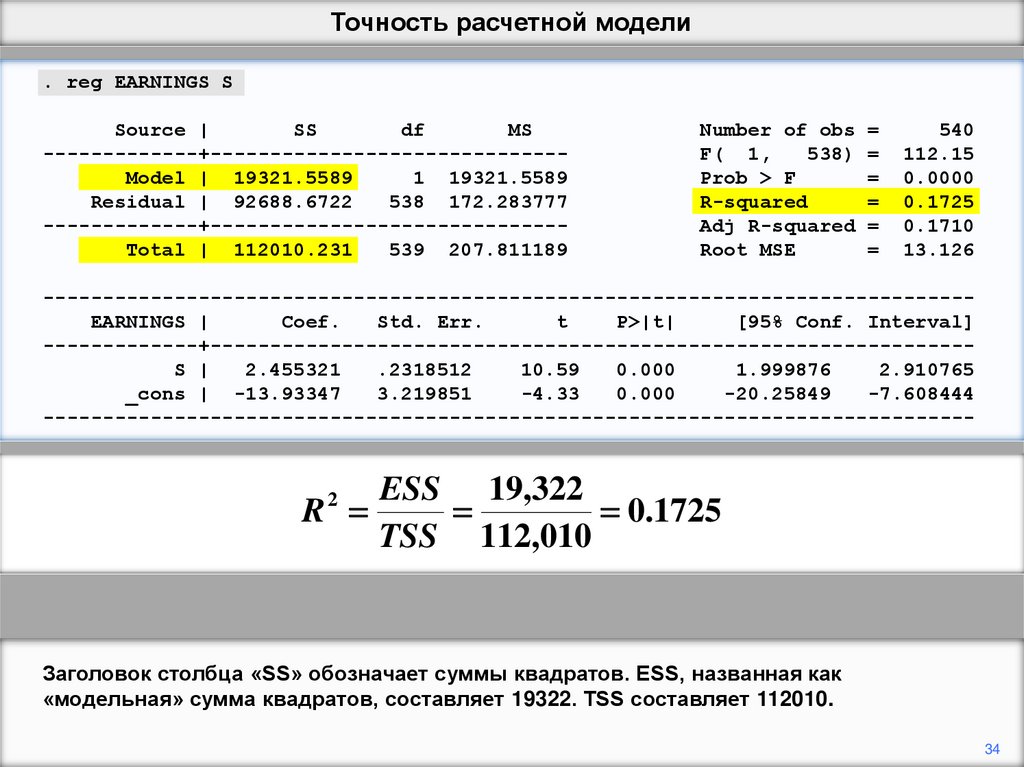
Заголовок столбца «SS» обозначает суммы квадратов. ESS, названная как
«модельная» сумма квадратов, составляет 19322. TSS составляет 112010.
34

35.

Точность расчетной модели
. reg EARNINGS S
Source |
SS
df
MS
-------------+-----------------------------Model | 19321.5589
1 19321.5589
Residual | 92688.6722
538 172.283777
-------------+-----------------------------Total | 112010.231
539 207.811189
Number of obs
F( 1,
538)
Prob > F
R-squared
Adj R-squared
Root MSE
=
=
=
=
=
=
540
112.15
0.0000
0.1725
0.1710
13.126
-----------------------------------------------------------------------------EARNINGS |
Coef.
Std. Err.
t
P>|t|
[95% Conf. Interval]
-------------+---------------------------------------------------------------S |
2.455321
.2318512
10.59
0.000
1.999876
2.910765
_cons | -13.93347
3.219851
-4.33
0.000
-20.25849
-7.608444
------------------------------------------------------------------------------
ESS 19,322
R
0.1725
TSS 112,010
2
Разделив ESS на TSS, мы имеем R2 = 19,322 / 112,010 = 0.1725, как указано в верхнем
правом углу слайда.
35

36.

Точность расчетной модели
. reg EARNINGS S
Source |
SS
df
MS
-------------+-----------------------------Model | 19321.5589
1 19321.5589
Residual | 92688.6722
538 172.283777
-------------+-----------------------------Total | 112010.231
539 207.811189
Number of obs
F( 1,
538)
Prob > F
R-squared
Adj R-squared
Root MSE
=
=
=
=
=
=
540
112.15
0.0000
0.1725
0.1710
13.126
-----------------------------------------------------------------------------EARNINGS |
Coef.
Std. Err.
t
P>|t|
[95% Conf. Interval]
-------------+---------------------------------------------------------------S |
2.455321
.2318512
10.59
0.000
1.999876
2.910765
_cons | -13.93347
3.219851
-4.33
0.000
-20.25849
-7.608444
------------------------------------------------------------------------------
ESS 19,322
R
0.1725
TSS 112,010
2
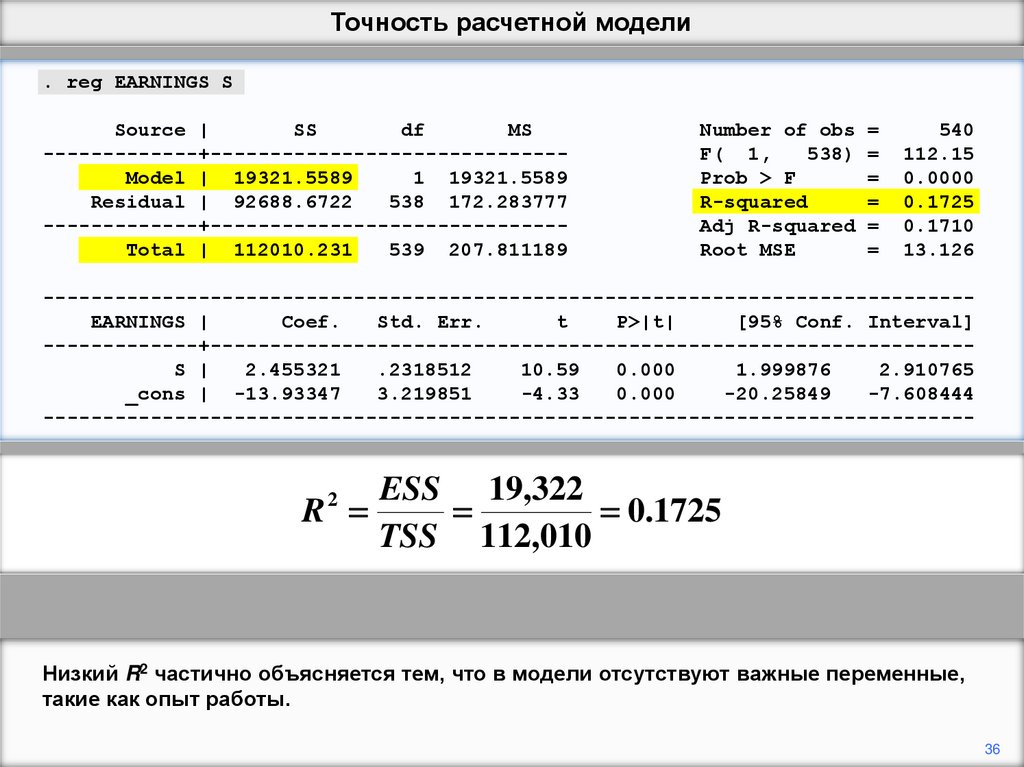
Низкий R2 частично объясняется тем, что в модели отсутствуют важные переменные,
такие как опыт работы.
36

37.

Точность расчетной модели
. reg EARNINGS S
Source |
SS
df
MS
-------------+-----------------------------Model | 19321.5589
1 19321.5589
Residual | 92688.6722
538 172.283777
-------------+-----------------------------Total | 112010.231
539 207.811189
Number of obs
F( 1,
538)
Prob > F
R-squared
Adj R-squared
Root MSE
=
=
=
=
=
=
540
112.15
0.0000
0.1725
0.1710
13.126
-----------------------------------------------------------------------------EARNINGS |
Coef.
Std. Err.
t
P>|t|
[95% Conf. Interval]
-------------+---------------------------------------------------------------S |
2.455321
.2318512
10.59
0.000
1.999876
2.910765
_cons | -13.93347
3.219851
-4.33
0.000
-20.25849
-7.608444
------------------------------------------------------------------------------
ESS 19,322
R
0.1725
TSS 112,010
2
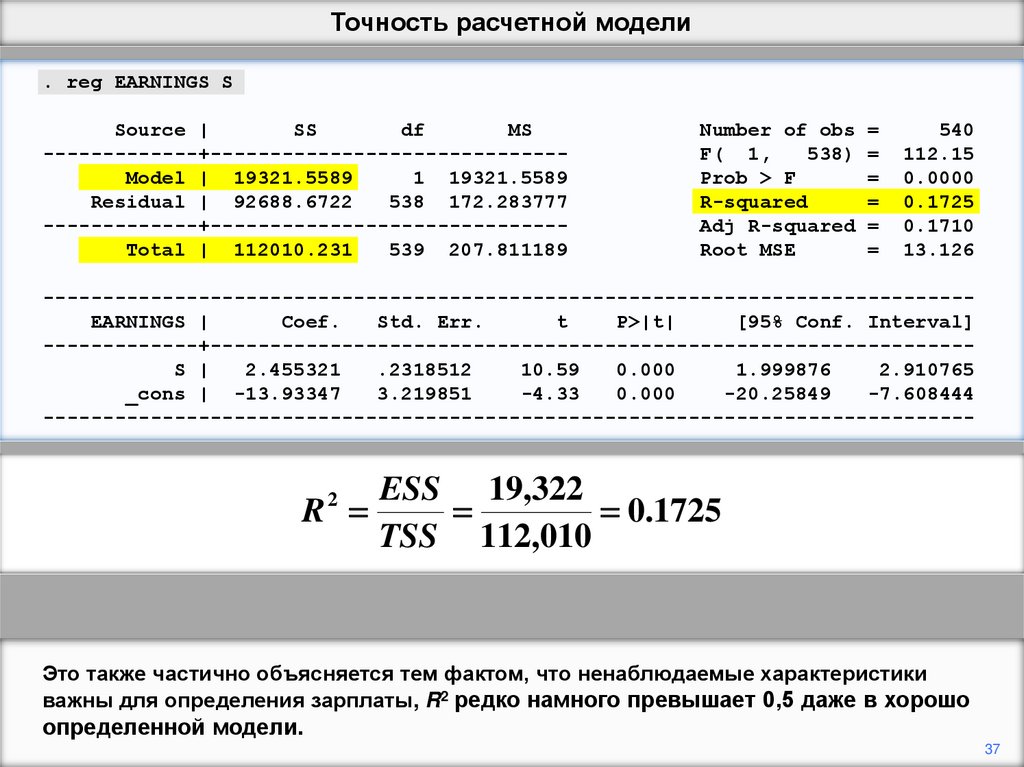
Это также частично объясняется тем фактом, что ненаблюдаемые характеристики
важны для определения зарплаты, R2 редко намного превышает 0,5 даже в хорошо
определенной модели.
37

38.

Точность расчетной модели
Y
i
Y
2
2
ˆ
Yi Y ei2
TSS ESS RSS
2
ˆ
(
Y
Y
)
ESS
i
R2
TSS (Yi Y ) 2
Мы хотим построить уравнение регрессии так, чтобы точность была максимально
возможной согласно R2 . Возможно ли это при определении b1 и b2 с помощью метода
наименьших квадратов?
38

39.

Точность расчетной модели
Y
i
Y
2
2
ˆ
Yi Y ei2
TSS ESS RSS
2
ˆ
(
Y
Y
)
ESS
i
R2
TSS (Yi Y ) 2
ei
TSS RSS
2
R
1
2
TSS
(
Y
Y
)
i
2
Чтобы увидеть это, перепишите выражение для R2 в терминах RSS.
39

40.

Точность расчетной модели
Y
i
Y
2
2
ˆ
Yi Y ei2
TSS ESS RSS
2
ˆ
(
Y
Y
)
ESS
i
R2
TSS (Yi Y ) 2
ei
TSS RSS
2
R
1
2
TSS
(
Y
Y
)
i
2
При МНК коэффициенты регрессии выбираются таким образом, чтобы
минимизировать сумму квадратов остатков. Из этого автоматически следует, что они
максимизируют R2.
40

41.

Точность расчетной модели
rY ,Yˆ
Yi Y Yˆi Y
2
2
ˆ
Yi Y Yi Y
2
ˆ
Yi Y
Y
i
Y
2
Yˆ Y
Y Y Yˆ Y
2
2
ˆ
Yi Y
2
Y
Y
i
i
2
2
i
i
R2
Другим критерием точности является корреляция между фактическими и расчетными
значениями Y. Если для расчета коэффициентов регрессии используется МНК, то
точность расчетной модели становится максимальной.
41

42.

Точность расчетной модели
rY ,Yˆ
Yi Y Yˆi Y
2
2
ˆ
Yi Y Yi Y
Yˆ Y
Y Y Yˆ Y
2
i
2
2
i
i
2
2
ˆ
ˆ
Yi Yˆ
Yi ˆ Y
Y2ˆi Y
Y R
Yi Y Yi 2 Y Yi e2i
Yi Y Yi Y
Yˆi Y ei Yˆi Y
Yi Yˆi ei
2
ˆ
Yi Y eiYˆi Y ei
2
ˆ
Yi Y
Заменим фактическое значение Y в первом сомножителе.
42

43.

Точность расчетной модели
rY ,Yˆ
Yi Y Yˆi Y
2
2
ˆ
Yi Y Yi Y
Yˆ Y
Y Y Yˆ Y
2
i
2
2
i
i
2
2
ˆ
ˆ
Yi Yˆ
Yi ˆ Y
Y2ˆi Y
Y R
Yi Y Yi 2 Y Yi e2i
Yi Y Yi Y
Yˆi Y ei Yˆi Y
2
ˆ
Yi Y eiYˆi Y ei
2
ˆ
Yi Y
Делаем перестановки.
43

44.

Точность расчетной модели
rY ,Yˆ
Yi Y Yˆi Y
2
2
ˆ
Yi Y Yi Y
Yˆ Y
Y Y Yˆ Y
2
i
2
2
i
i
2
2
ˆ
ˆ
Yi Yˆ
Yi ˆ Y
Y2ˆi Y
Y R
Yi Y Yi 2 Y Yi e2i
Yi Y Yi Y
Yˆi Y ei Yˆi Y
2
ˆ
Yi Y eiYˆi Y ei
2
ˆ
Yi Y Yˆi ei 0
e
i
0
Разложим выражение. Последние два члена равны нулю.
44

45.

Точность расчетной модели
rY ,Yˆ
Yi Y Yˆi Y
2
2
ˆ
Yi Y Yi Y
Yˆ Y
Y Y Yˆ Y
2
i
2
2
i
i
2
2
ˆ
ˆ
Yi Yˆ
Yi ˆ Y
Y2ˆi Y
Y R
Yi Y Yi 2 Y Yi e2i
Yi Y Yi Y
Yˆi Y ei Yˆi Y
2
ˆ
Yi Y eiYˆi Y ei
2
ˆ
Yi Y
Таким образом, числитель равен сумме квадратов отклонений расчетных значений Y
от среднего значения Y.
45

46.

Точность расчетной модели
rY ,Yˆ
Yi Y Yˆi Y
2
2
ˆ
Yi Y Yi Y
2
ˆ
Yi Y
Y
i
Y
2
Yˆ Y
Y Y Yˆ Y
2
2
ˆ
Yi Y
2
Y
Y
i
i
2
2
i
i
R2
Мы имеем то же выражение под квадратным корнем в знаменателе. Следовательно,
это выражение под квадратным корнем остается в числителе.
46

47.

Точность расчетной модели
rY ,Yˆ
Yi Y Yˆi Y
2
2
ˆ
Yi Y Yi Y
2
ˆ
Yi Y
Y
i
Y
2
Yˆ Y
Y Y Yˆ Y
2
2
ˆ
Yi Y
2
Yi Y
i
2
2
i
i
R2
Таким образом, коэффициент корреляции является квадратным корнем из R2. Что и
требовалось доказать.
47