Множественная регрессия с двумя независимыми переменными

1.

МНОЖЕСТВЕННАЯ РЕГРЕССИЯ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ:
ПРИМЕР
EARNINGS = b1 + b2S + b3EXP + u
b1
EARNINGS
EXP
S
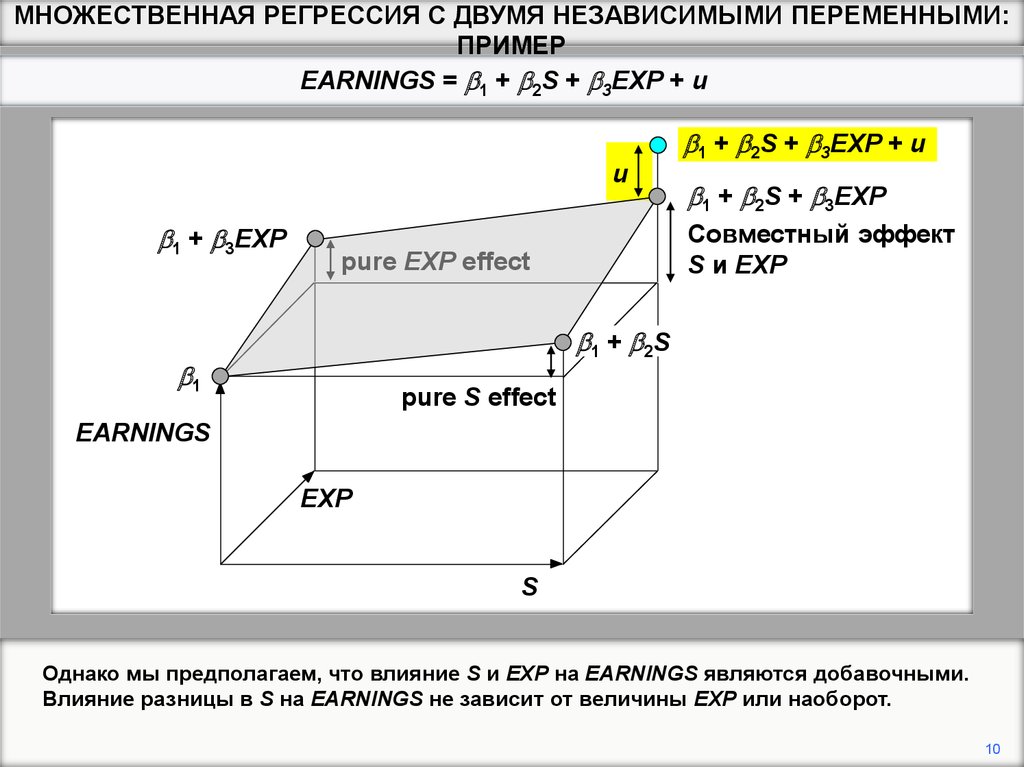
Эта последовательность обеспечивает геометрическую интерпретацию модели
множественной регрессии с двумя объясняющими переменными.
1

2.

МНОЖЕСТВЕННАЯ РЕГРЕССИЯ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ:
ПРИМЕР
EARNINGS = b1 + b2S + b3EXP + u
b1
EARNINGS
EXP
S
В частности, мы рассмотрим модель функции заработка, где почасовой заработок,
EARNINGS, зависит от количества лет обучения (наивысший оконченный класс), S, и
опыта работы в годах, EXP.
2

3.

МНОЖЕСТВЕННАЯ РЕГРЕССИЯ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ:
ПРИМЕР
EARNINGS = b1 + b2S + b3EXP + u
b1
EARNINGS
EXP
S
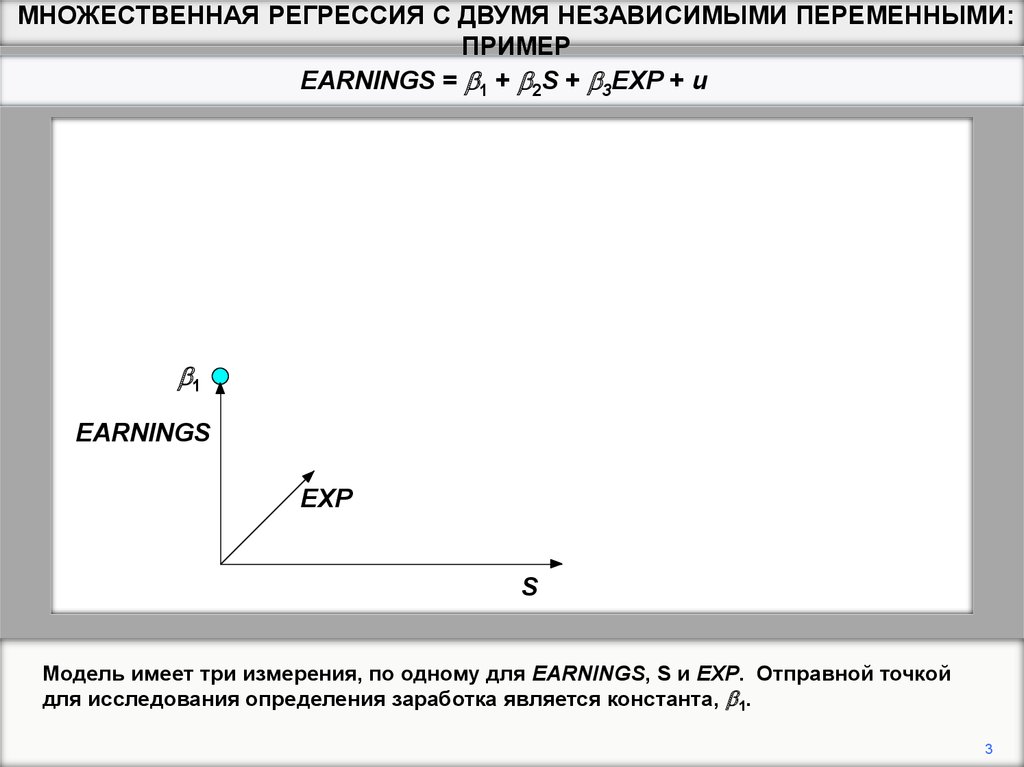
Модель имеет три измерения, по одному для EARNINGS, S и EXP. Отправной точкой
для исследования определения заработка является константа, b1.
3

4.

МНОЖЕСТВЕННАЯ РЕГРЕССИЯ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ:
ПРИМЕР
EARNINGS = b1 + b2S + b3EXP + u
b1
EARNINGS
EXP
S
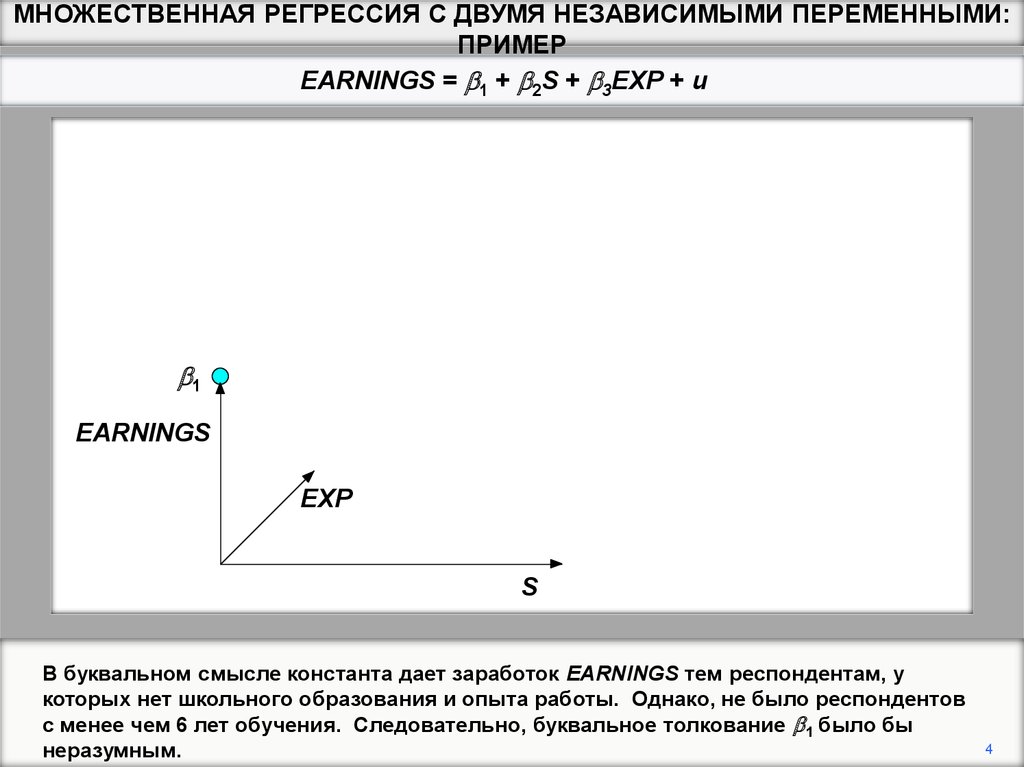
В буквальном смысле константа дает заработок EARNINGS тем респондентам, у
которых нет школьного образования и опыта работы. Однако, не было респондентов
с менее чем 6 лет обучения. Следовательно, буквальное толкование b1 было бы
неразумным.
4

5.

МНОЖЕСТВЕННАЯ РЕГРЕССИЯ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ:
ПРИМЕР
EARNINGS = b1 + b2S + b3EXP + u
b 1 + b 2S
b1
pure S effect
EARNINGS
EXP
S
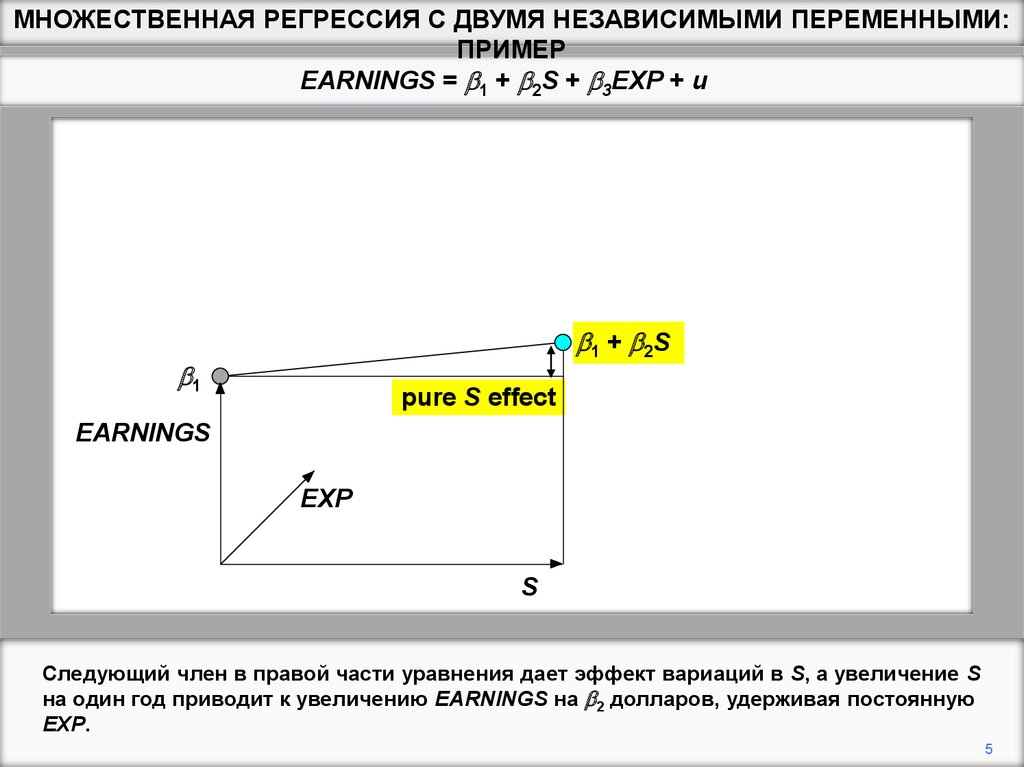
Следующий член в правой части уравнения дает эффект вариаций в S, а увеличение S
на один год приводит к увеличению EARNINGS на b2 долларов, удерживая постоянную
EXP.
5

6.

МНОЖЕСТВЕННАЯ РЕГРЕССИЯ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ:
ПРИМЕР
EARNINGS = b1 + b2S + b3EXP + u
b1 + b3EXP
pure EXP effect
b1
EARNINGS
EXP
S
Аналогичным образом, третий член дает эффект вариаций в EXP. Увеличение EXP на
один год приводит к увеличению прибыли на b3 долларов, оставляя S постоянным.
6

7.

МНОЖЕСТВЕННАЯ РЕГРЕССИЯ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ:
ПРИМЕР
EARNINGS = b1 + b2S + b3EXP + u
b1 + b2S + b3EXP
b1 + b3EXP
совместный эффект
S и EXP
pure EXP effect
b 1 + b 2S
b1
pure S effect
EARNINGS
EXP
S
Различные комбинации S и EXP увеличивают значения EARNINGS, которые лежат на
плоскости, показанной на диаграмме, определяемой уравнением EARNINGS = b1 + b2S
+ b3EXP. Это нестохастическая (неслучайная) составляющая модели.
7

8.

МНОЖЕСТВЕННАЯ РЕГРЕССИЯ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ:
ПРИМЕР
EARNINGS = b1 + b2S + b3EXP + u
b1 + b2S + b3EXP + u
u
b1 + b3EXP
b1 + b2S + b3EXP
Совместный эффект
S и EXP
pure EXP effect
b 1 + b 2S
b1
pure S effect
EARNINGS
EXP
S
Последним элементом модели является остаточный член, u. Это приводит к тому, что
фактические значения EARNINGS отклоняются от плоскости. В этом наблюдении u
имеет положительное значение.
8

9.

МНОЖЕСТВЕННАЯ РЕГРЕССИЯ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ:
ПРИМЕР
EARNINGS = b1 + b2S + b3EXP + u
b1 + b2S + b3EXP + u
u
b1 + b3EXP
b1 + b2S + b3EXP
Совместный эффект
S и EXP
pure EXP effect
b 1 + b 2S
b1
pure S effect
EARNINGS
EXP
S
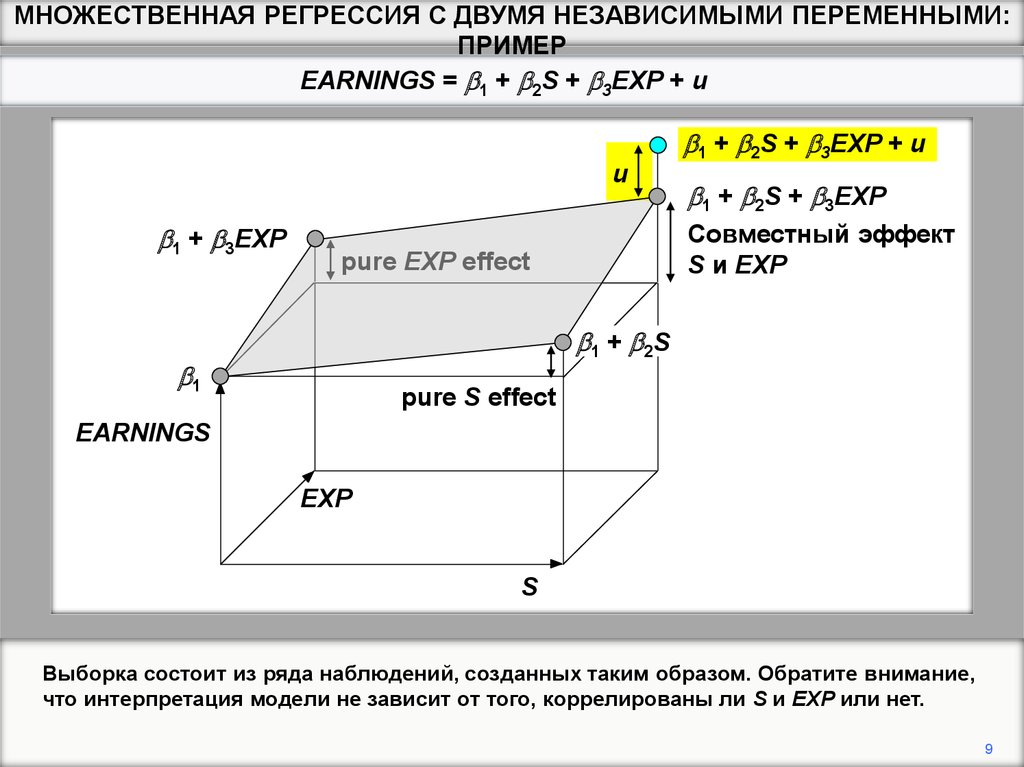
Выборка состоит из ряда наблюдений, созданных таким образом. Обратите внимание,
что интерпретация модели не зависит от того, коррелированы ли S и EXP или нет.
9

10.

МНОЖЕСТВЕННАЯ РЕГРЕССИЯ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ:
ПРИМЕР
EARNINGS = b1 + b2S + b3EXP + u
b1 + b2S + b3EXP + u
u
b1 + b3EXP
b1 + b2S + b3EXP
Совместный эффект
S и EXP
pure EXP effect
b 1 + b 2S
b1
pure S effect
EARNINGS
EXP
S
Однако мы предполагаем, что влияние S и EXP на EARNINGS являются добавочными.
Влияние разницы в S на EARNINGS не зависит от величины EXP или наоборот.
10

11.

МНОЖЕСТВЕННАЯ РЕГРЕССИЯ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ:
ПРИМЕР
Истинная модель
Подогнанная модель
Y b1 b 2 X 2 b 3 X 3 u
Yˆ b1 b2 X 2 b3 X 3
Коэффициенты регрессии рассчитываются по тому же принципу наименьших
квадратов, что и при простом регрессионном анализе. Установленное значение Y в
наблюдении i зависит от нашего выбора b1, b2, и b3.
11

12.

МНОЖЕСТВЕННАЯ РЕГРЕССИЯ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ:
ПРИМЕР
Истинная модель
Подогнанная модель
Y b1 b 2 X 2 b 3 X 3 u
Yˆ b1 b2 X 2 b3 X 3
uˆ i Yi Yˆi Yi b1 b2 X 2 i b3 X 3 i
Остаток ei в наблюдении i - это разница между фактическим и установленным
значениями Y.
12

13.

МНОЖЕСТВЕННАЯ РЕГРЕССИЯ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ:
ПРИМЕР
Истинная модель
Подогнанная модель
Y b1 b 2 X 2 b 3 X 3 u
Yˆ b1 b2 X 2 b3 X 3
uˆ i Yi Yˆi Yi b1 b2 X 2 i b3 X 3 i
RSS uˆ Yi b1 b2 X 2 i b3 X 3 i
2
i
2
Мы определяем RSS, сумму квадратов остатков, и выбираем b1, b2, и b3 , чтобы
минимизировать его.
13

14.

МНОЖЕСТВЕННАЯ РЕГРЕССИЯ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ:
ПРИМЕР
Истинная модель
Подогнанная модель
Y b1 b 2 X 2 b 3 X 3 u
Yˆ b1 b2 X 2 b3 X 3
uˆ i Yi Yˆi Yi b1 b2 X 2 i b3 X 3 i
RSS uˆ Yi b1 b2 X 2 i b3 X 3 i
2
i
2
(Yi 2 b12 b22 X 22i b32 X 32i 2b1Yi 2b2 X 2 iYi
2b3 X 3 iYi 2b1b2 X 2 i 2b1b3 X 3 i 2b2 b3 X 2 i X 3 i )
Yi 2 nb12 b22 X 22i b32 X 32i 2b1 Yi
2b2 X 2 iYi 2b3 X 3 iYi 2b1b2 X 2 i
2b1b3 X 3 i 2b2 b3 X 2 i X 3 i
Сначала мы раскладываем RSS как показано сверху.
14

15.

МНОЖЕСТВЕННАЯ РЕГРЕССИЯ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ:
ПРИМЕР
Истинная модель
Подогнанная модель
Y b1 b 2 X 2 b 3 X 3 u
Yˆ b1 b2 X 2 b3 X 3
uˆ i Yi Yˆi Yi b1 b2 X 2 i b3 X 3 i
RSS Yi 2 nb12 b22 X 22i b32 X 32i 2b1 Yi
2b2 X 2 iYi 2b3 X 3 iYi 2b1b2 X 2 i
2b1b3 X 3 i 2b2 b3 X 2 i X 3 i
RSS
0
b1
RSS
0
b2
RSS
0
b3
Затем мы используем условия первого порядка для его минимизации.
15

16.

МНОЖЕСТВЕННАЯ РЕГРЕССИЯ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ:
ПРИМЕР
Истинная модель
Подогнанная модель
Y b1 b 2 X 2 b 3 X 3 u
Yˆ bˆ1 bˆ2 X 2 bˆ3 X 3
2
X
X
Y
Y
X
X
2i 2 i 3i 3
X 3 i X 3 Yi Y X 2 i X 2 X 3 i X 3
ˆ
b2
2
2
2
X 2i X 2 X 3i X 3 X 2i X 2 X 3 i X 3
bˆ1 Y bˆ2 X 2 bˆ3 X 3
Таким образом, мы получаем три уравнения на три неизвестных. Решая эти
уравнения, получаем выражения для конкретных значений, удовлетворяющих
критерию МНК. (Выражение для bˆ совпадает с выражением для bˆ , с индексами 2 и
2
3
3, которые поменяны местами.)
16

17.

МНОЖЕСТВЕННАЯ РЕГРЕССИЯ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ:
ПРИМЕР
Истинная модель
Подогнанная модель
Y b1 b 2 X 2 b 3 X 3 u
Yˆ bˆ1 bˆ2 X 2 bˆ3 X 3
2
X
X
Y
Y
X
X
2i 2 i 3i 3
X 3 i X 3 Yi Y X 2 i X 2 X 3 i X 3
ˆ
b2
2
2
2
X 2i X 2 X 3i X 3 X 2i X 2 X 3i X 3
bˆ1 Y bˆ2 X 2 bˆ3 X 3
Выражение для bˆ1 является прямым продолжением выражения для него в простом
регрессионном анализе.
17

18.

МНОЖЕСТВЕННАЯ РЕГРЕССИЯ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ:
ПРИМЕР
Истинная модель
Подогнанная модель
Y b1 b 2 X 2 b 3 X 3 u
Yˆ bˆ1 bˆ2 X 2 bˆ3 X 3
2
X
X
Y
Y
X
X
2i 2 i 3i 3
X 3 i X 3 Yi Y X 2 i X 2 X 3 i X 3
ˆ
b2
2
2
2
X 2i X 2 X 3i X 3 X 2i X 2 X 3i X 3
bˆ1 Y bˆ2 X 2 bˆ3 X 3
Однако выражения для коэффициентов наклона значительно сложнее, чем для
коэффициента наклона в простом регрессионном анализе.
18

19.

МНОЖЕСТВЕННАЯ РЕГРЕССИЯ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ:
ПРИМЕР
Истинная модель
Подогнанная модель
Y b1 b 2 X 2 b 3 X 3 u
Yˆ bˆ1 bˆ2 X 2 bˆ3 X 3
2
X
X
Y
Y
X
X
2i 2 i 3i 3
X 3 i X 3 Yi Y X 2 i X 2 X 3 i X 3
ˆ
b2
2
2
2
X 2i X 2 X 3i X 3 X 2i X 2 X 3i X 3
bˆ1 Y bˆ2 X 2 bˆ3 X 3
Для общего случая, когда существует много объясняющих переменных, обычная
алгебра непригодна. Необходимо перейти на матричную алгебру.
19

20.

МНОЖЕСТВЕННАЯ РЕГРЕССИЯ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ:
ПРИМЕР
. reg EARNINGS S EXP
---------------------------------------------------------------------------Source |
SS
df
MS
Number of obs =
500
-----------+-----------------------------F( 2,
497) =
35.24
Model | 8735.42401
2
4367.712
Prob > F
= 0.0000
Residual | 61593.5422
497 123.930668
R-squared
= 0.1242
-----------+-----------------------------Adj R-squared = 0.1207
Total | 70328.9662
499 140.939812
Root MSE
= 11.132
---------------------------------------------------------------------------EARNINGS |
Coef.
Std. Err.
t
P>|t|
[95% Conf. Interval]
-----------+---------------------------------------------------------------S |
1.877563
.2237434
8.39
0.000
1.437964
2.317163
EXP |
.9833436
.2098457
4.69
0.000
.5710495
1.395638
_cons | -14.66833
4.288375
-3.42
0.001
-23.09391
-6.242752
----------------------------------------------------------------------------
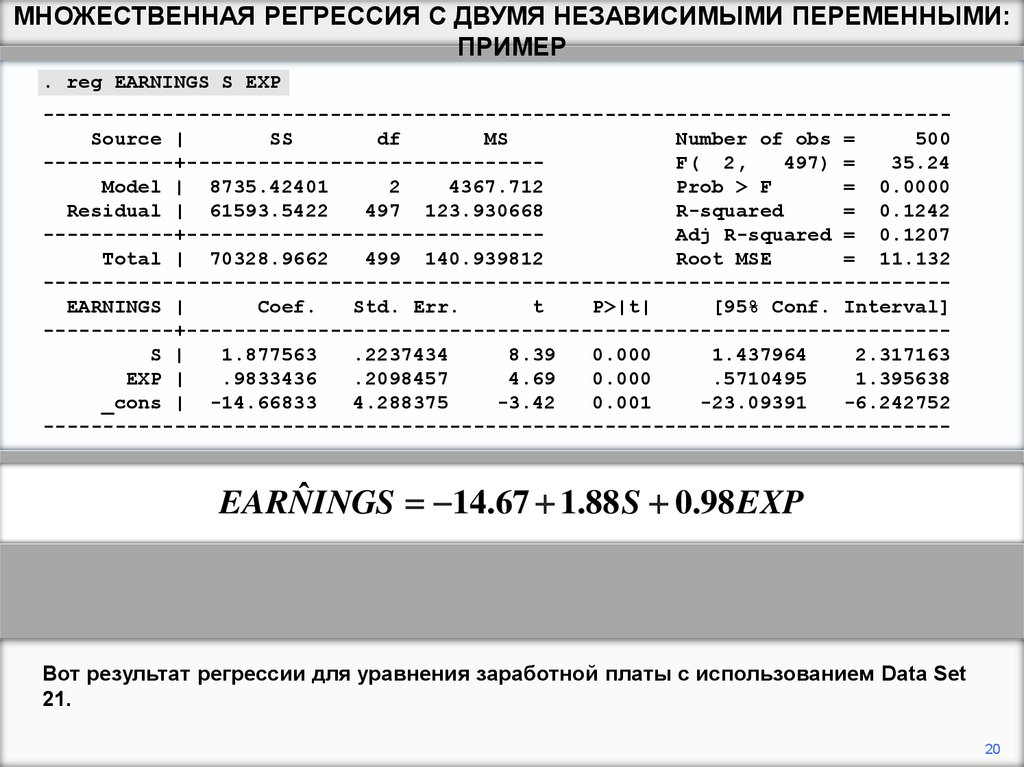
ˆ
EARNINGS
14.67 1.88 S 0.98 EXP
Вот результат регрессии для уравнения заработной платы с использованием Data Set
21.
20

21.

МНОЖЕСТВЕННАЯ РЕГРЕССИЯ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ:
ПРИМЕР
. reg EARNINGS S EXP
---------------------------------------------------------------------------Source |
SS
df
MS
Number of obs =
500
-----------+-----------------------------F( 2,
497) =
35.24
Model | 8735.42401
2
4367.712
Prob > F
= 0.0000
Residual | 61593.5422
497 123.930668
R-squared
= 0.1242
-----------+-----------------------------Adj R-squared = 0.1207
Total | 70328.9662
499 140.939812
Root MSE
= 11.132
---------------------------------------------------------------------------EARNINGS |
Coef.
Std. Err.
t
P>|t|
[95% Conf. Interval]
-----------+---------------------------------------------------------------S |
1.877563
.2237434
8.39
0.000
1.437964
2.317163
EXP |
.9833436
.2098457
4.69
0.000
.5710495
1.395638
_cons | -14.66833
4.288375
-3.42
0.001
-23.09391
-6.242752
----------------------------------------------------------------------------
ˆ
EARNINGS
14.67 1.88 S 0.98 EXP
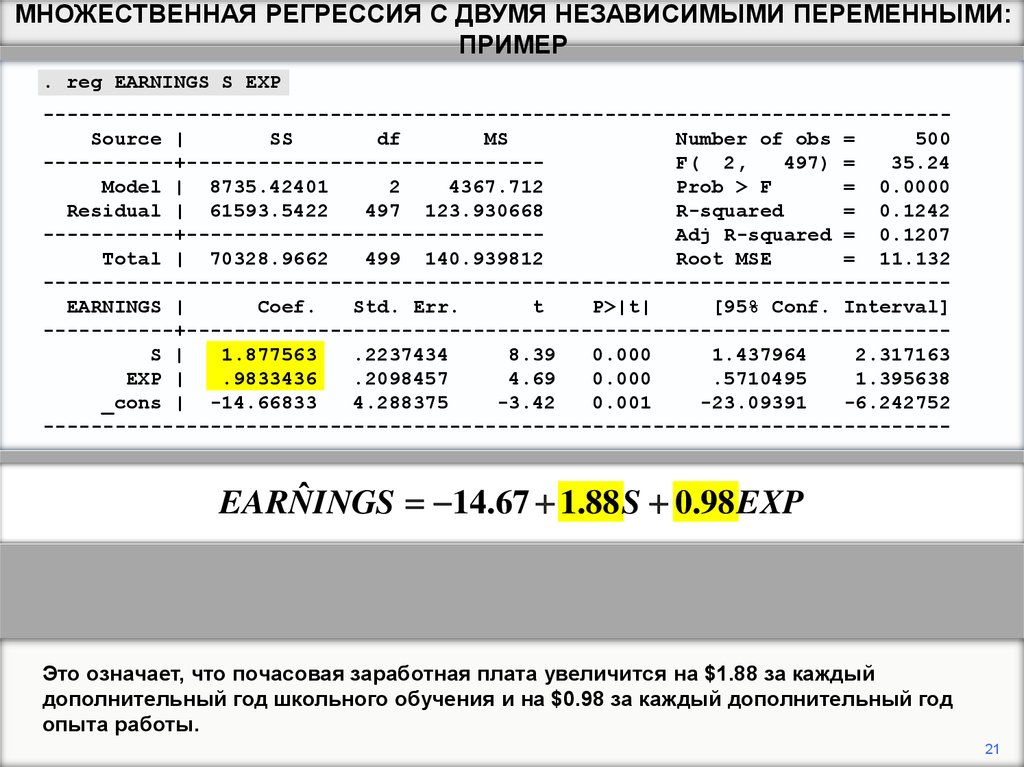
Это означает, что почасовая заработная плата увеличится на $1.88 за каждый
дополнительный год школьного обучения и на $0.98 за каждый дополнительный год
опыта работы.
21

22.

МНОЖЕСТВЕННАЯ РЕГРЕССИЯ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ:
ПРИМЕР
. reg EARNINGS S EXP
---------------------------------------------------------------------------Source |
SS
df
MS
Number of obs =
500
-----------+-----------------------------F( 2,
497) =
35.24
Model | 8735.42401
2
4367.712
Prob > F
= 0.0000
Residual | 61593.5422
497 123.930668
R-squared
= 0.1242
-----------+-----------------------------Adj R-squared = 0.1207
Total | 70328.9662
499 140.939812
Root MSE
= 11.132
---------------------------------------------------------------------------EARNINGS |
Coef.
Std. Err.
t
P>|t|
[95% Conf. Interval]
-----------+---------------------------------------------------------------S |
1.877563
.2237434
8.39
0.000
1.437964
2.317163
EXP |
.9833436
.2098457
4.69
0.000
.5710495
1.395638
_cons | -14.66833
4.288375
-3.42
0.001
-23.09391
-6.242752
----------------------------------------------------------------------------
ˆ
EARNINGS
14.67 1.88 S 0.98 EXP
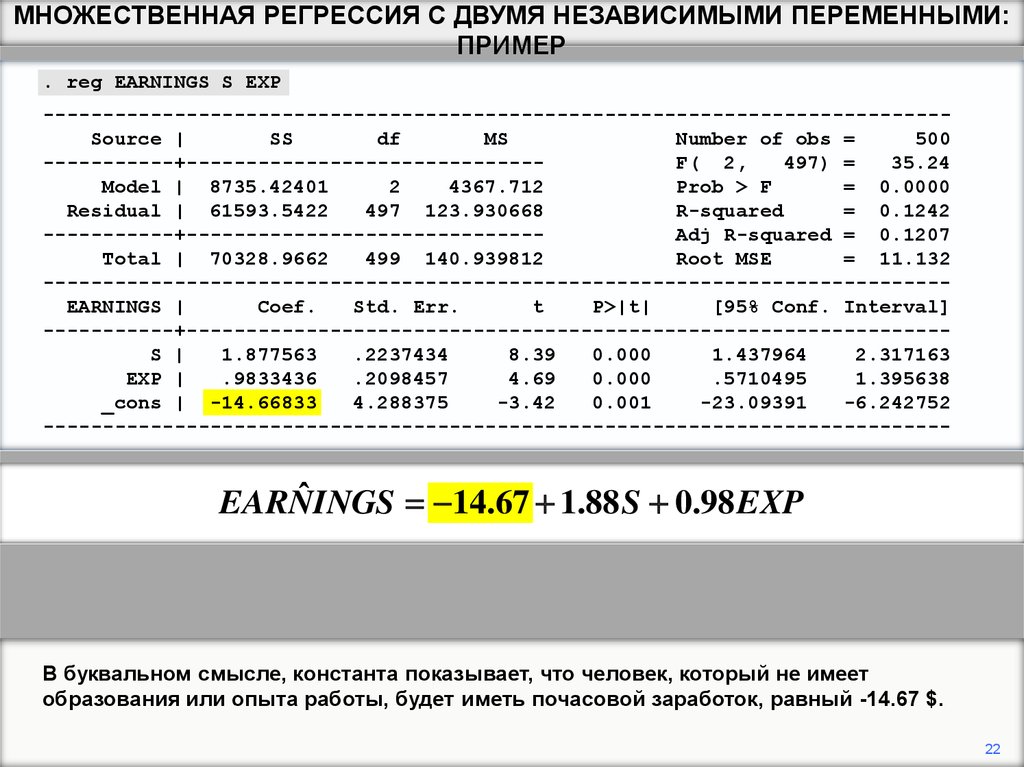
В буквальном смысле, константа показывает, что человек, который не имеет
образования или опыта работы, будет иметь почасовой заработок, равный -14.67 $.
22

23.

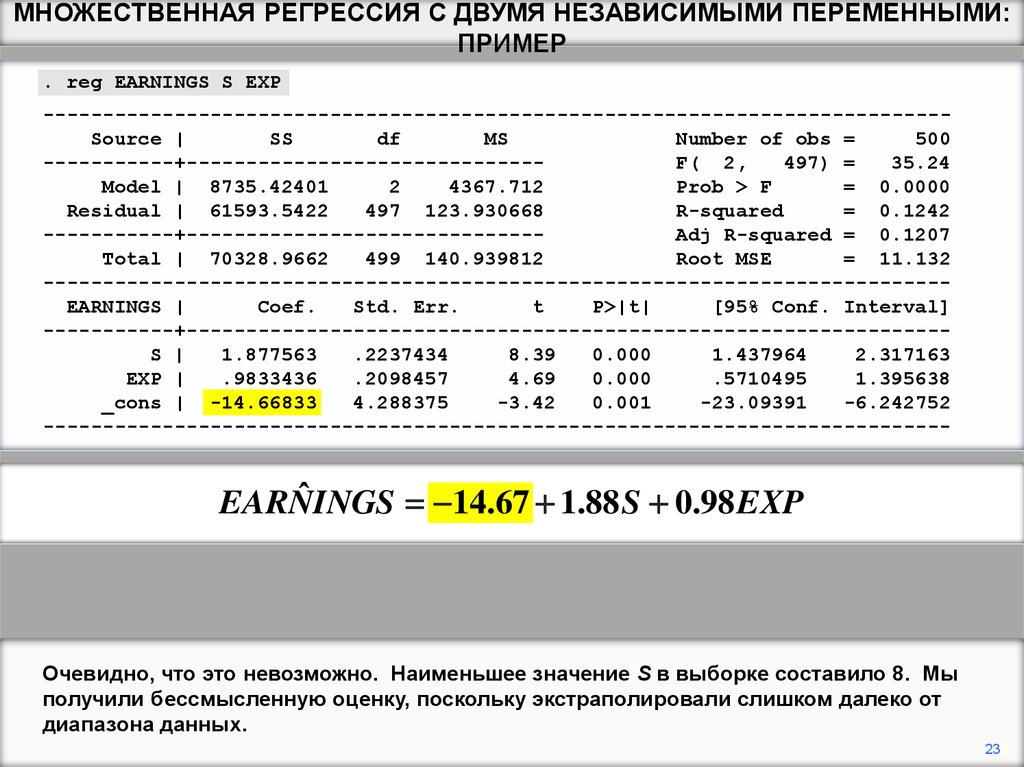
МНОЖЕСТВЕННАЯ РЕГРЕССИЯ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ:
ПРИМЕР
. reg EARNINGS S EXP
---------------------------------------------------------------------------Source |
SS
df
MS
Number of obs =
500
-----------+-----------------------------F( 2,
497) =
35.24
Model | 8735.42401
2
4367.712
Prob > F
= 0.0000
Residual | 61593.5422
497 123.930668
R-squared
= 0.1242
-----------+-----------------------------Adj R-squared = 0.1207
Total | 70328.9662
499 140.939812
Root MSE
= 11.132
---------------------------------------------------------------------------EARNINGS |
Coef.
Std. Err.
t
P>|t|
[95% Conf. Interval]
-----------+---------------------------------------------------------------S |
1.877563
.2237434
8.39
0.000
1.437964
2.317163
EXP |
.9833436
.2098457
4.69
0.000
.5710495
1.395638
_cons | -14.66833
4.288375
-3.42
0.001
-23.09391
-6.242752
----------------------------------------------------------------------------
ˆ
EARNINGS
14.67 1.88 S 0.98 EXP
Очевидно, что это невозможно. Наименьшее значение S в выборке составило 8. Мы
получили бессмысленную оценку, поскольку экстраполировали слишком далеко от
диапазона данных.
23