Планирование эксперимента. Анализ результатов. Планирование 2-го порядка

1. Планирование эксперимента. Анализ результатов. Планирование 2-го порядка.

2. Пример проведения планирования 1-го порядка. Постановка задачи

Покупатели приходят в магазин с одним продавцом.
Время между приходом покупателей и время обслуживания
подчиняются экспоненциальному закону.
Необходимо определить функциональную зависимость между
временем прихода, временем обслуживания и средним
временем нахождения покупателя в очереди:
Тср.оч.= f(Тприх, Тобсл)
-?
Предполагаем линейную зависимость.
Пусть время прихода – в пределах от 5.0 до 6.0 мин.
время обслуж. – в пределах от 3.5 до 3.8 мин.
Тогда:
-1
+1
Тприх: 5
6
Тобсл: 3.5
3.8

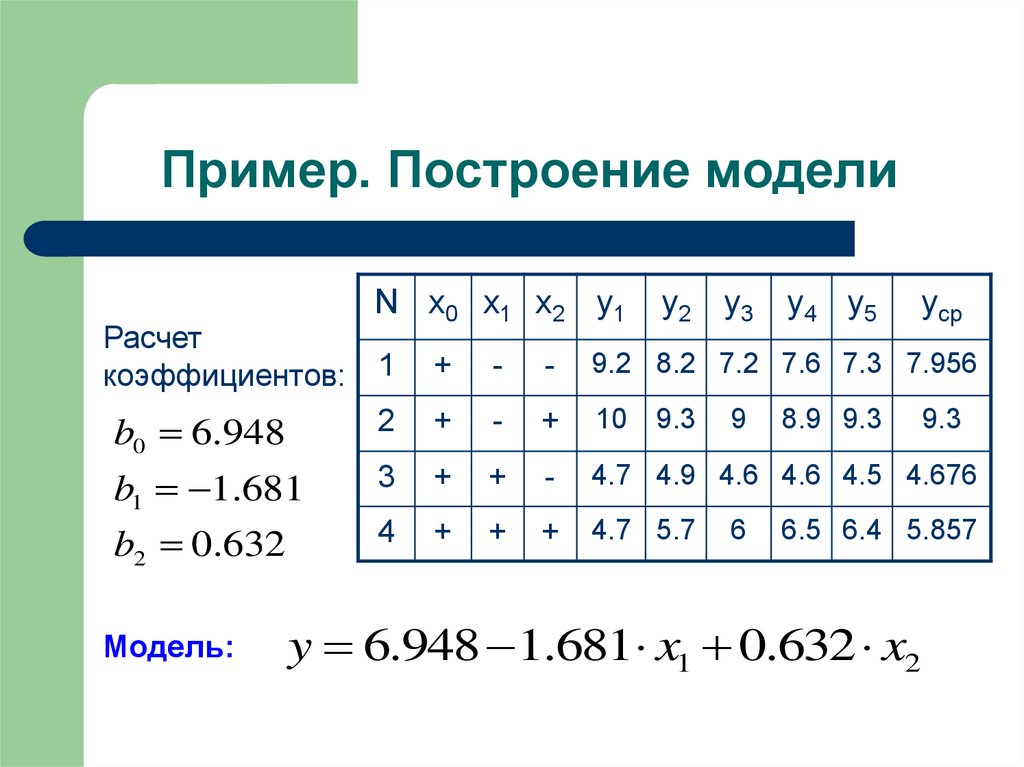
3. Пример. Построение модели

Расчет
коэффициентов:
N x0 x1 x2 y1
y2 y3 y4 y5
yср
1
+
-
-
9.2 8.2 7.2 7.6 7.3 7.956
b0 6.948
2
+
-
+
10
b1 1.681
3
+
+
-
4.7 4.9 4.6 4.6 4.5 4.676
b2 0.632
4
+
+
+
4.7 5.7
Модель:
9.3
9
6
8.9 9.3
9.3
6.5 6.4 5.857
y 6.948 1.681 x1 0.632 x2

4. Пример. Проверка адекватности

Выборочная дисперсия:
Дисперсия адекватности:
S 2 0.382
S ад2 0.034
S ад2
Критерий Фишера: F
1
2
S
Модель
адекватна

5. Пример. Проверка линейности

Опыт в центре эксперимента:
N x0 x1 x2
-1
Тприх: 5
Тобсл: 3.5
1
+1
6
3.8
0
+
…
-
-
yср
7.956
…
…
4
+
+
+
5
+
0
0
5.857

6. Пример. Проверка линейности

Опыт в центре эксперимента:
N x0 x1 x2
-1
Тприх: 5
Тобсл: 3.5
1
+1
6
3.8
Критерий Стьюдента:
t
b0 y0 N
S
2
0
5.5
3.65
+
…
-
-
yср
7.956
…
…
4
+
+
+
5.857
5
+
0
0
7.791
2.73 tтабл 2.131
Модель НЕ
линейна

7. Пример. Проверка значимости коэффициентов

Модель:
y 69.48 16.81 x1 6.32 x2
Критерий Стьюдента:
Коэффициенты:
t
bi N
S
2
t табл
t1 5.44
Значим
t 2 2.04
НЕ Значим

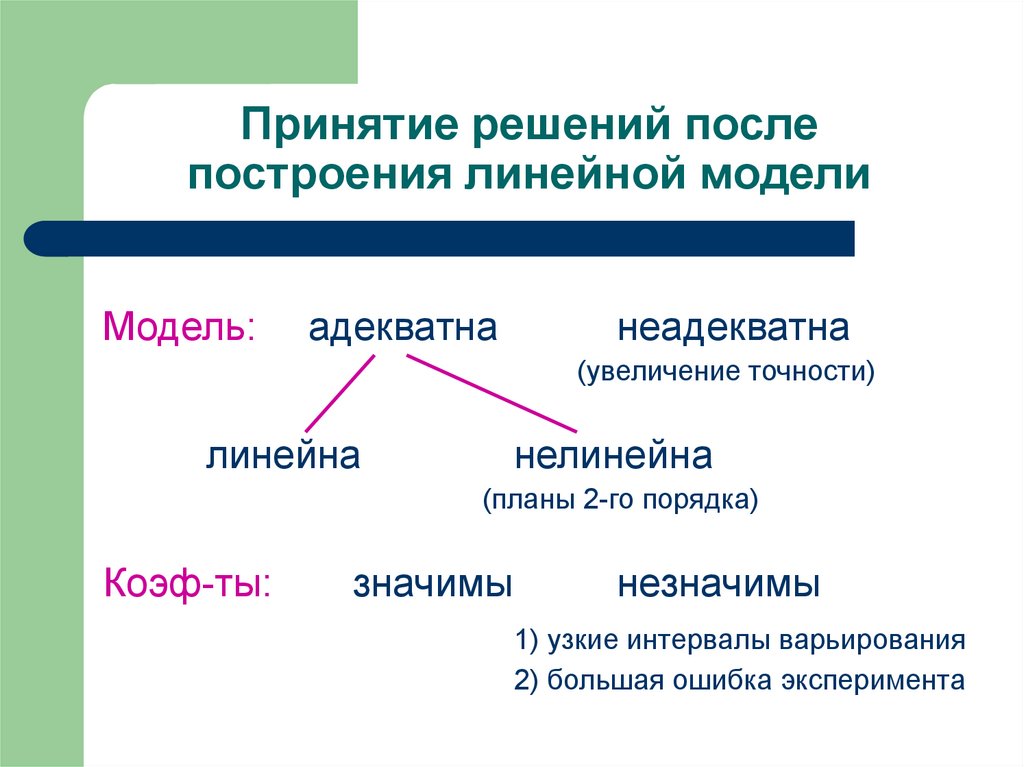
8. Принятие решений после построения линейной модели

Модель:
адекватна
неадекватна
(увеличение точности)
линейна
нелинейна
(планы 2-го порядка)
Коэф-ты:
значимы
незначимы
1) узкие интервалы варьирования
2) большая ошибка эксперимента

9. Планы второго порядка

Уравнение второго порядка
k
y b 0 bi xi
i 1
ПФЭ
N ?k
k
2
b
x
x
b
x
ij i j ii i
1 i j k
i 1

10. Планы второго порядка

Уравнение второго порядка
k
y b 0 bi xi
i 1
ПФЭ
N 3k
k
2
b
x
x
b
x
ij i j ii i
1 i j k
i 1
Центральный композиционный план
N N 0 2k n0
N0 2
k l
Опыты из планир-я
1-го порядка

11. Центральный композиционный план (ЦКП) для двух факторов

y b0 b1 x1 b2 x2 b12 x1 x2 b11 x12 b22 x22
x2
5 уровней:
α
+1
-α -1
0
+1 +α
-1
+1
-1
x1

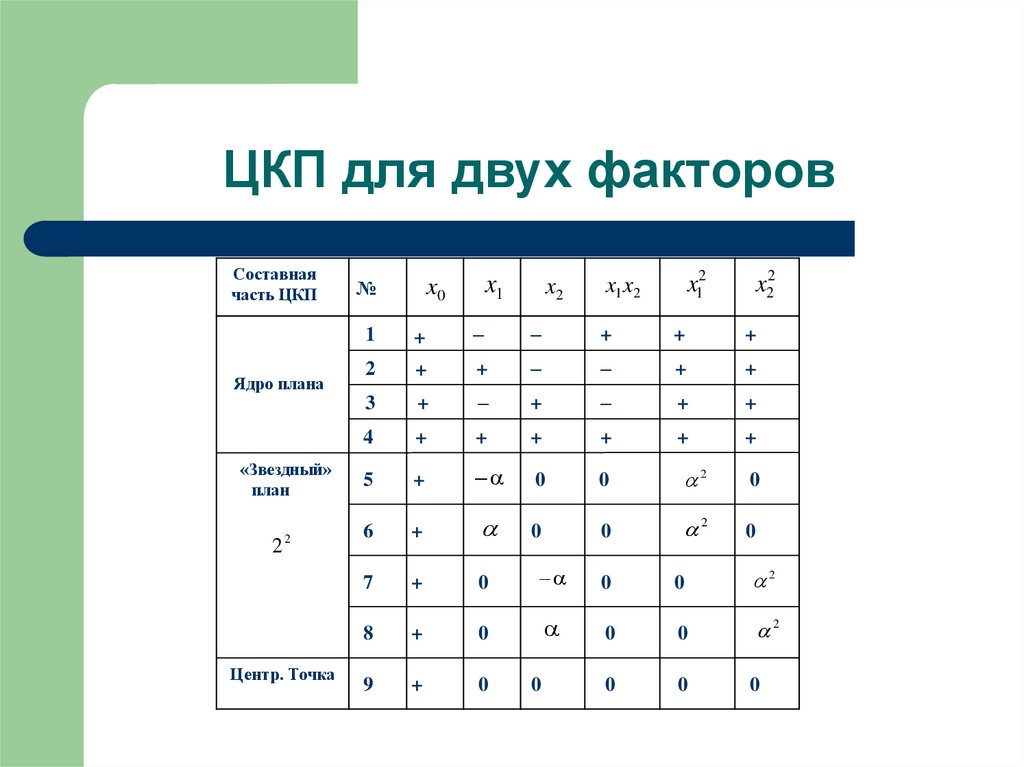
12. ЦКП для двух факторов

Составная
часть ЦКП
Ядро плана
«Звездный»
план
2
2
Центр. Точка
№
x1
x0
x2
x12
x1 x2
x22
1
+
–
–
+
+
+
2
+
+
–
–
+
+
3
+
–
+
–
+
+
4
+
+
+
+
+
+
5
+
0
0
2
0
6
+
0
0
2
0
7
+
0
0
0
2
8
+
0
0
0
2
9
+
0
0
0
0
0

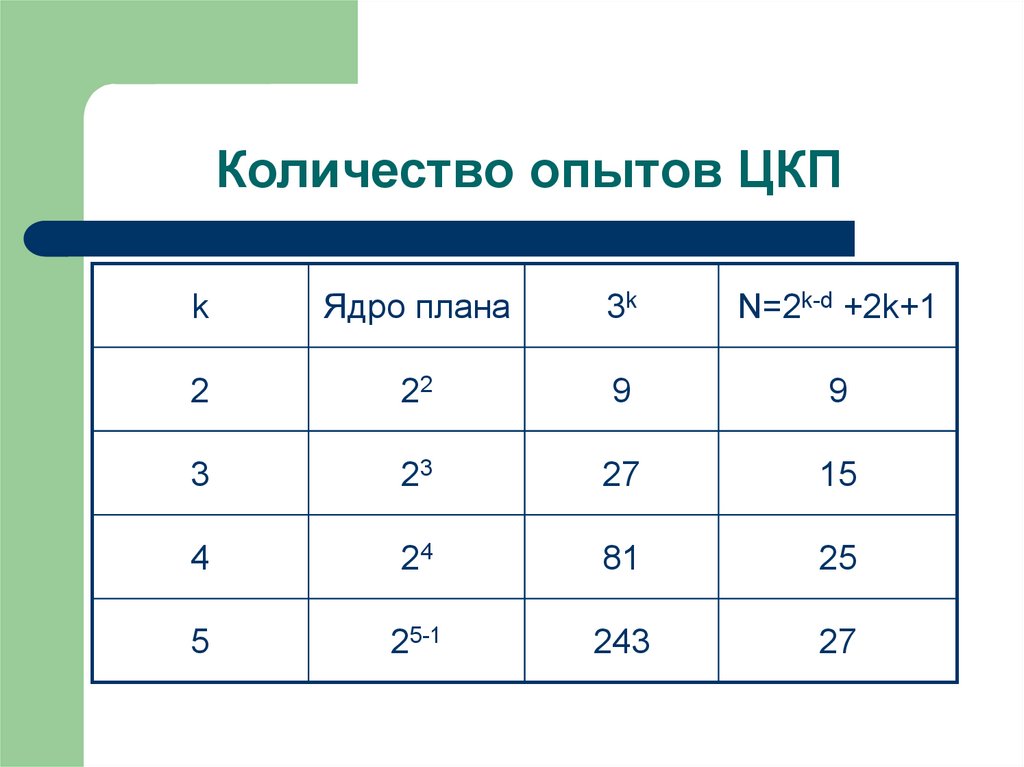
13. Количество опытов ЦКП

k
Ядро плана
3k
N=2k-d +2k+1
2
22
9
9
3
23
27
15
4
24
81
25
5
25-1
243
27

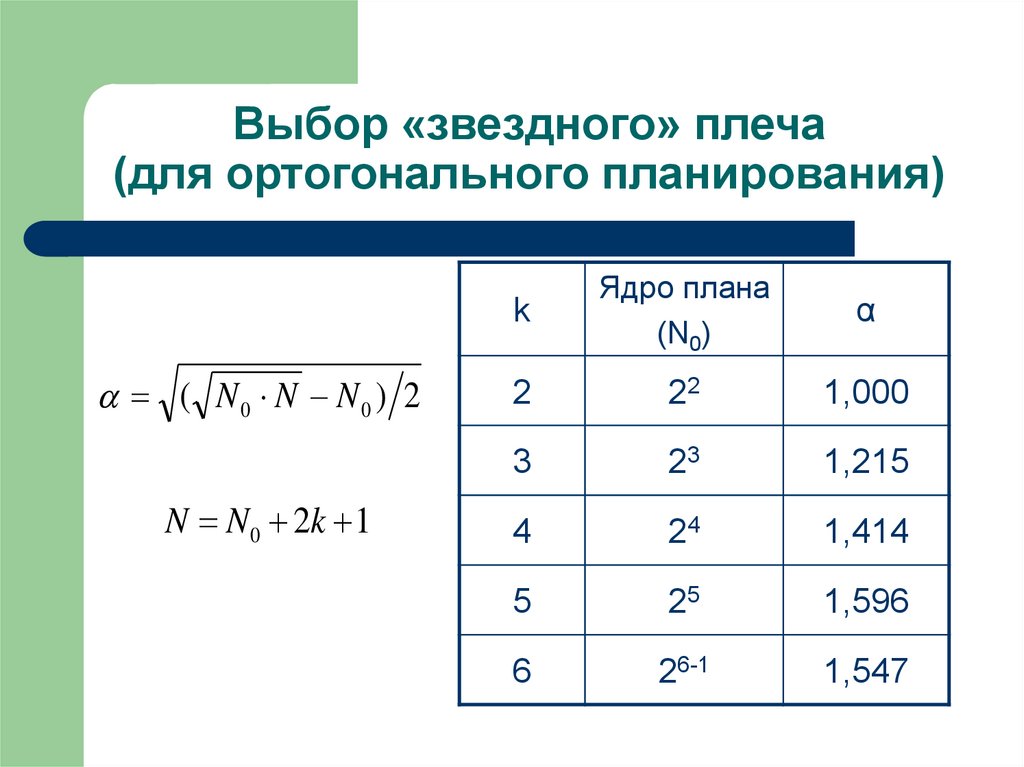
14. Выбор «звездного» плеча (для ортогонального планирования)

( N0 N N0 ) 2
N N 0 2k 1
k
Ядро плана
(N0)
α
2
22
1,000
3
23
1,215
4
24
1,414
5
25
1,596
6
26-1
1,547

15. Расчет коэффициентов

Пусть b0 b1 b2 b3 b12=b4 b13=b5 b23=b6 b11=b7 …
N
bi
x
l 1
N
il
yl
2
x
il
l 1
N
b0
y
l 1
N
l

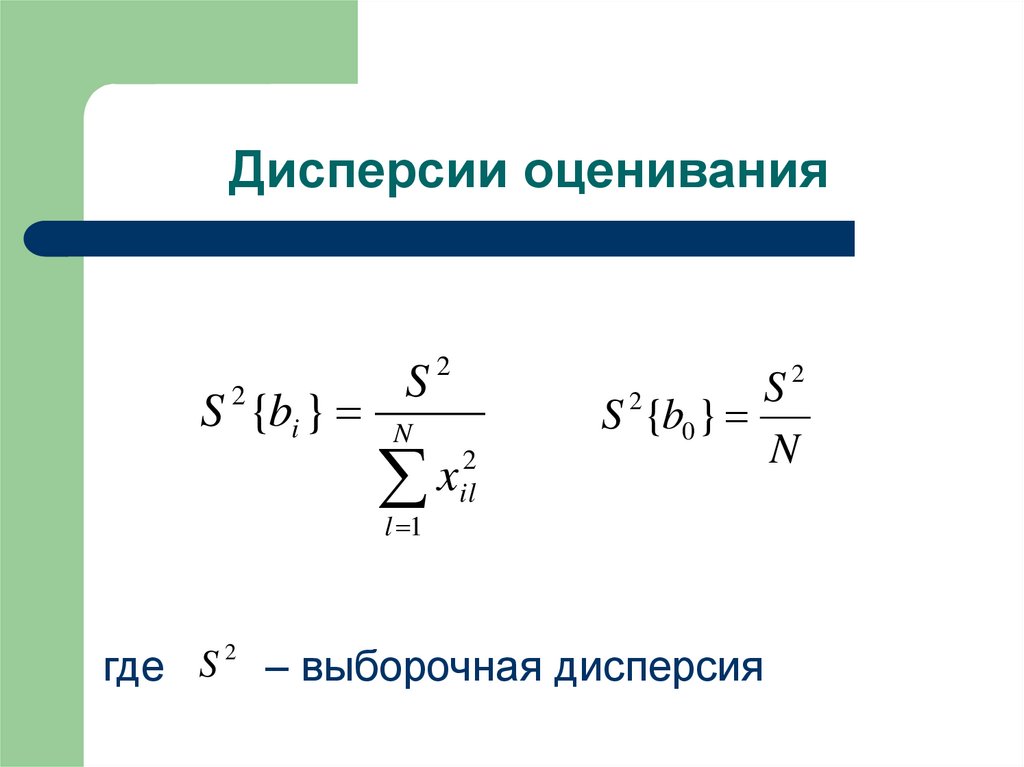
16. Дисперсии оценивания

S 2 {bi }
S
2
N
x
l 1
2
il
2
S
2
S {b0 }
N
2
S
где
– выборочная дисперсия

17. Проверка значимости коэффициентов

Критерий Стьюдента:
t расч
bi
S 2 {bi }
Коэффициент значим, если
t расч t табл ( ; f N (n 1))

18. Задача оценки точности

Задача 1: оценка точности и достоверности при заданном
методе реализации модели, при заданном объеме
выборки;
Задача 2: оценка необходимого числа реализаций при
заданных точности и достоверности результатов.
Желаемую степень точности можно задавать:
а) в виде доли стандартного отклонения;
б) в процентах от величины среднего значения;
в) в абсолютных величинах.

19. Оценивание среднего значения совокупности (задача 2)

Задача: необходимо построить такую оценку истинного
среднего значения совокупности, что
P d X d 1
где
X — выборочное среднее,
1 — вероятность того, что интервал
содержит
d
X
Необходимый для этого условия объем выборки:
n Z / 2 d 2
2
где
Z 2— двусторонняя стандартная нормальная статистика (допустимая
величина риска);
d — допустимая разность между оценкой и истинным значением
параметра;
— величина изменчивости совокупности,

20. Оценивание среднего значения совокупности (задача 1)

Задача: какой точности d мы достигнем при заданном
объеме выборки n?
P d X d 1
Достигаемая точность:
d
где
S 2 t
n
S 2 — выборочная дисперсия, полученная на выборке n;
t
— критерий Стьюдента

21. Пример. Оценка точности

- неизвестна.
Точность в долях стандартного отклонения:
d
4
Необходимый для этого условия объем выборки:
при 0.05
Z / 2
n
2
d2
Z 2 1.96
2 Z 2 2 4 2
2
16
1
.
96
61.46 62
2

22. Оценивание дисперсии совокупности

Задача: построение доверительных интервалов
P (1 d ) 2 S 2 (1 d ) 2 1
где
0 d 1 — число, характеризующее степень близости оценки S 2
к истинной дисперсии
2
.
Необходимый для этого условия объем выборки:
n 1
2 Z
d2
2
2

23. Сравнение двух распределений

Задача: проверка близости распределения отклика
модели к некоторому другому распределению.
Под желаемой точностью (d ) будем понимать максимальную
разность сравниваемых распределений во всех точках
Необходимый для этого условия объем выборки:
n
d
2
где — табличное значение функции Колмогорова.

24. Стратегическое и тактическое планирование

Стратегическое планирование (первая
составляющая планирования экспериментов с
моделями систем) ставит целью решение задачи
получения необходимой информации о системе с
помощью модели, с учетом ограничения на ресурсы.
Тактическое планирование (вторая составляющая) —
это определение способа проведения каждой серии
испытаний модели, предусмотренных планом
эксперимента.

25. Некоторые проблемы стратегического планирования

сложность построения плана
эксперимента;
наличие большого количества
факторов;
многокомпонентность функции
отклика;
ограниченность ресурсов проведения
эксперимента.

26. Этапы стратегического планирования

построение структурной модели
осуществляется исходя из того, что
должно быть сделано;
построение функциональной модели
производится исходя из того, что может
быть сделано.

27. Структурная модель

Структурная модель плана эксперимента
характеризуется числом факторов и числом уровней
для каждого фактора.
Число элементов эксперимента
где
N c q1q2 ...qk
,
k — число факторов эксперимента;
qi — число уровней i-го фактора.
Число уровней зависит от предполагаемой функциональной
зависимости между откликом и факторами.
qi q j
Если уровни равноотстоят друг от друга и если
для всех факторов, то получаем ПФЭ q-го порядка.
Nc qk

28. Функциональная модель

Функциональная модель определяет
количество необходимых элементов
структурной модели .
Модель полная, если
N ф N(ПФЭ),
c
Модель неполная, если
N ф N c (ДФЭ).

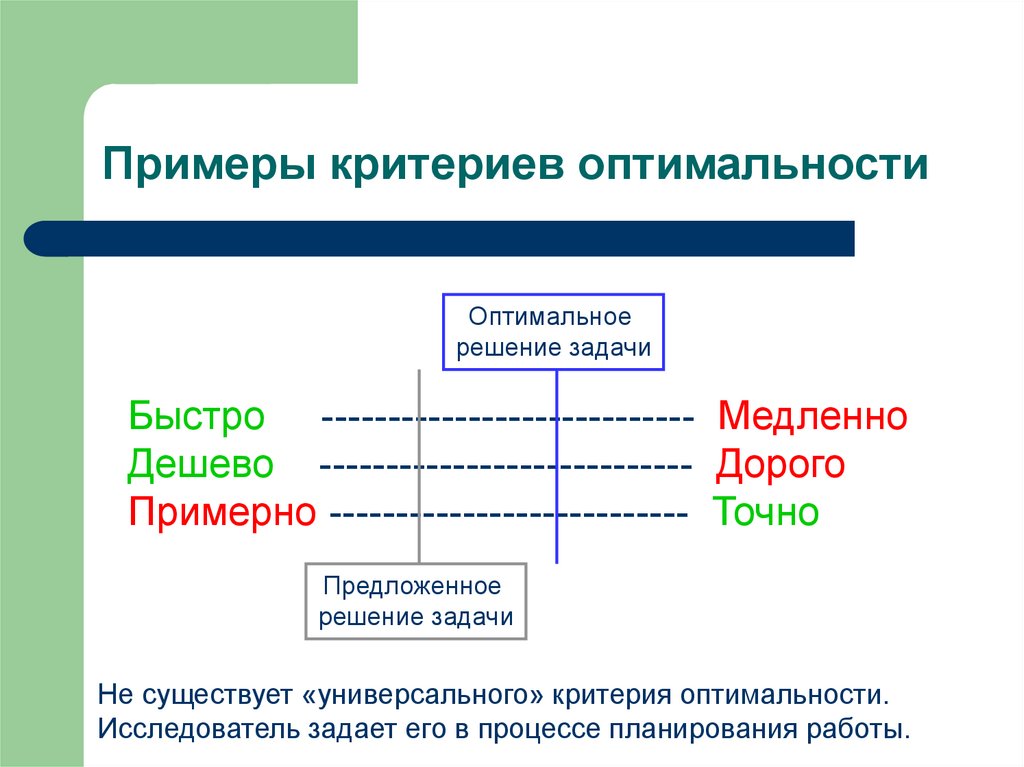
29. Примеры критериев оптимальности

Оптимальное
решение задачи
Быстро ---------------------------- Медленно
Дешево ---------------------------- Дорого
Примерно --------------------------- Точно
Предложенное
решение задачи
Не существует «универсального» критерия оптимальности.
Исследователь задает его в процессе планирования работы.

30. Выбор критерия оптимальности

Если для каждого из экспериментов,
приводящих к желаемому результату, можно
оценить величину «затрат», то задача
заключается в выборе такого эксперимента,
при котором «затраты» минимальны.
«Стоимостный» подход возможен только в
том случае, когда все эксперименты приводят
к одинаковой точности результата.

31. Подбор компонентов функциональной модели

Можно варьировать: количество факторов
k,
q ,
число уровней
количество повторений эксперимента p .
Учитываются: затраты времени на 1 опыт ,
c .
стоимость опыта
Полное число опытов при симметрично повторяемом
эксперименте:
k
N pq
Общее время, требуемое для проведение эксперимента:
T N
Общие затраты:
С с T

32. Пример. Стратегия поездки из пункта А в пункт Б

Из пункта А в пункт Б можно попасть разными путями, за
разное время, затратив разное количество денег (горючее,
амортизация а/м, штрафы, заработок за счет попутных
пассажиров). Каждый водитель формирует свой критерий
оптимальности, например:
Экономия денег (аккуратная езда, выбор оптимальной
скорости, соблюдение правил, подбор попутчиков) за счет
времени;
Экономия времени (быстрая езда) за счет денег (штрафы,
без попутчиков, повышенный износ автомашины),
безопасности, душевного спокойствия и комфорта (тряска,
рывки).
Повышение безопасности за счет времени;
Сохранение душевного спокойствия (избегание улиц с
интенсивным движением, строгое выполнение правил) за
счет времени и денег (более длинный путь).