Похожие презентации:
Обобщенная линейная модель множественной регрессии с автокоррелированными остатками. (Лекция 5)
1.
Обобщенная линейная модельмножественной регрессии с
автокоррелированными остатками
2.
Автокорреляциярегрессионных остатков – корреляционная
зависимость текущих и предыдущих значений регрессионных остатков.
Линейная модель множественной регрессии
Y X ,
для которой нарушено 5 условие
Гаусса-Маркова называется
обобщенной линейной моделью множественной регрессии (ОЛММР) с
автокоррелированными остатками, а именно:
1) х1,…,хк – детерминированные переменные;
2) ранг матрицы Х равен "к+1" – среди признаков нет линейно
зависимых;
3) M i 0 , i 1, n - нет систематических ошибок в измерении у;
4) D i M i2 2 , i 1, n
5) cov( i , j ) M ( i j ) 0 , i j , i 1, n j 1, n
T
4') M 2 0
дисперсии.
( i2 2j ), т.е. на диагонали стоят равные
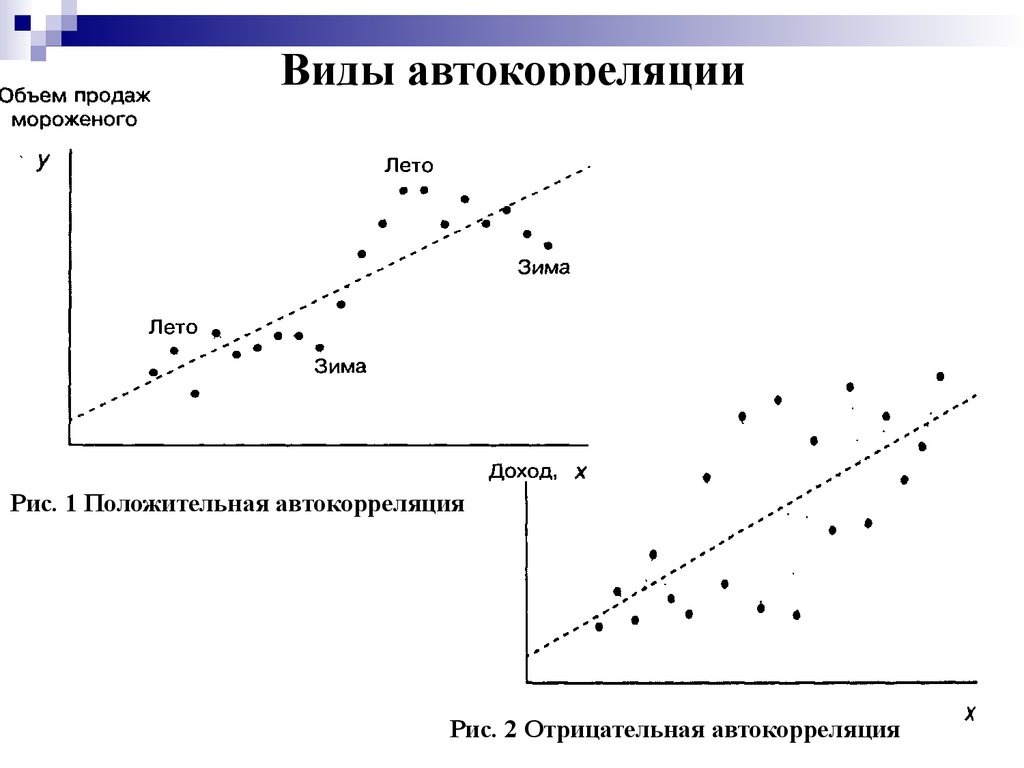
3. Виды автокорреляции
Рис. 1 Положительная автокорреляцияРис. 2 Отрицательная автокорреляция
4. Пример влияния автокорреляции на случайную выборку
Рассмотрим выборку из 50 независимыхнормально распределенных с нулевым
средним значений i.
С целью ознакомления с влиянием
автокорреляции будем вводить в нее
положительную, а затем отрицательную
автокорреляцию.
5. Пример влияния автокорреляции на случайную выборку
32
1
0
1
-1
-2
-3
ut 0.0ut 1 t
6. Пример влияния автокорреляции на случайную выборку
32
1
0
1
-1
-2
-3
ut 0.1ut 1 t
7. Пример влияния автокорреляции на случайную выборку
32
1
0
1
-1
-2
-3
ut 0.2ut 1 t
8. Пример влияния автокорреляции на случайную выборку
32
1
0
1
-1
-2
-3
ut 0.3ut 1 t
9. Пример влияния автокорреляции на случайную выборку
32
1
0
1
-1
-2
-3
ut 0.4ut 1 t
10. Пример влияния автокорреляции на случайную выборку
32
1
0
1
-1
-2
-3
ut 0.5ut 1 t
11. Пример влияния автокорреляции на случайную выборку
32
1
0
1
-1
-2
-3
ut 0.6ut 1 t
12. Пример влияния автокорреляции на случайную выборку
32
1
0
1
-1
-2
-3
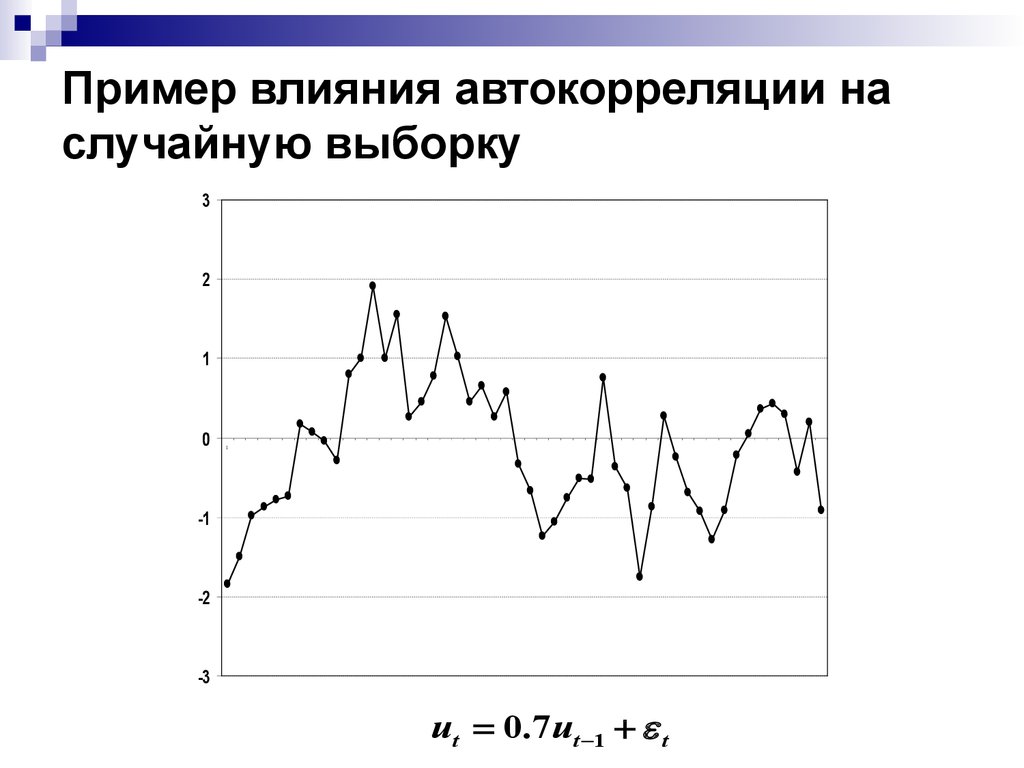
ut 0.7 ut 1 t
13. Пример влияния автокорреляции на случайную выборку
32
1
0
1
-1
-2
-3
ut 0.8ut 1 t
14. Пример влияния автокорреляции на случайную выборку
32
1
0
1
-1
-2
-3
ut 0.9ut 1 t
15. Пример влияния автокорреляции на случайную выборку
32
1
0
1
-1
-2
-3
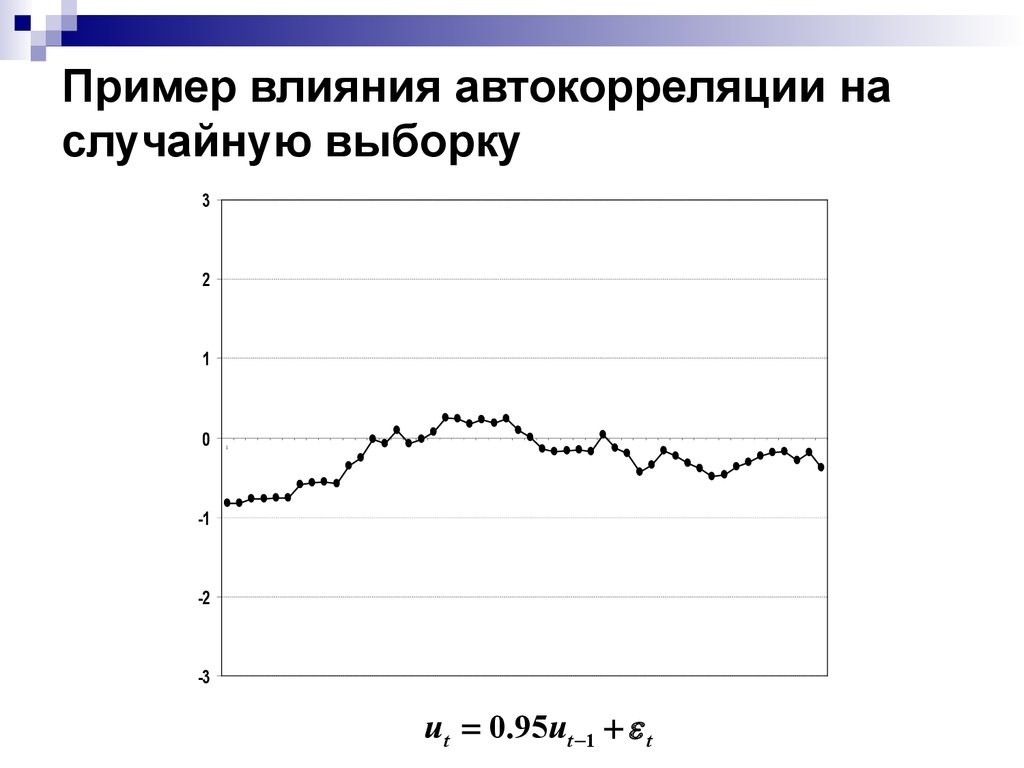
ut 0.95ut 1 t
16. Пример влияния автокорреляции на случайную выборку
32
1
0
1
-1
-2
-3
ut 0.0ut 1 t
17. Пример влияния автокорреляции на случайную выборку
32
1
0
1
-1
-2
-3
ut 0.3ut 1 t
18. Пример влияния автокорреляции на случайную выборку
32
1
0
1
-1
-2
-3
ut 0.6ut 1 t
19. Пример влияния автокорреляции на случайную выборку
32
1
0
1
-1
-2
-3
ut 0.9ut 1 t
20. Автокорреляция первого порядка
21. Автокорреляция первого порядка
12
1
2
0 2
1
2
1
...
...
...
n 1 n 2 n 3
... n 1
n 2
...
... n 3 ,
... ...
... 1
0
1
2
1
1
1
2
0
0
1
1 2
...
...
...
0
0
0
... 0
... 0
... 0
... ...
... 1
22. Обнаружение автокорреляции
1. Графический анализ статистической информации23. Обнаружение автокорреляции
2. Статистика Дарбина-УотсонаН0: 0 (нет явления автокорреляции)
Н1: 0 (есть явление автокорреляции)
n
DW
2
(
e
e
)
i i 1
i 2
n 1
.
2
e
i
i 1
Так как
n
(e e
i 2
i
i 1
n
n
n
n
i 2
i 2
) (e 2ei ei 1 e ) e 2 ei ei 1 e
2
i 2
2
i
DW
2
i 1
i 2
2
i
2 ei2 ei ei 1
2
e
i
2
i 1
2 1 r
ei ei 1
n
n
2 e 2 ei ei 1
i 2
2
i
i 2
24.
1. d в < DW <4- dв , то гипотеза об отсутствии автокорреляциипринимается.
2. d н < DW < dв или 4- dв < DW <4- d н , область неопределенности
критерия (вопрос об отвержении или принятии гипотезы остается
открытым).
3. 0< DW < d н , то принимается альтернативная гипотеза о
положительной автокорреляции.
4. 4- d н < DW <4, то принимается альтернативная гипотеза об
отрицательной автокорреляции.
25.
Примерисследования
регрессионных
остатков на автокорреляции
На основе наблюдений по десяти семьям
требуется
исследовать
зависимость
между
ежегодным потреблением бананов и годовым
семейным доходом.
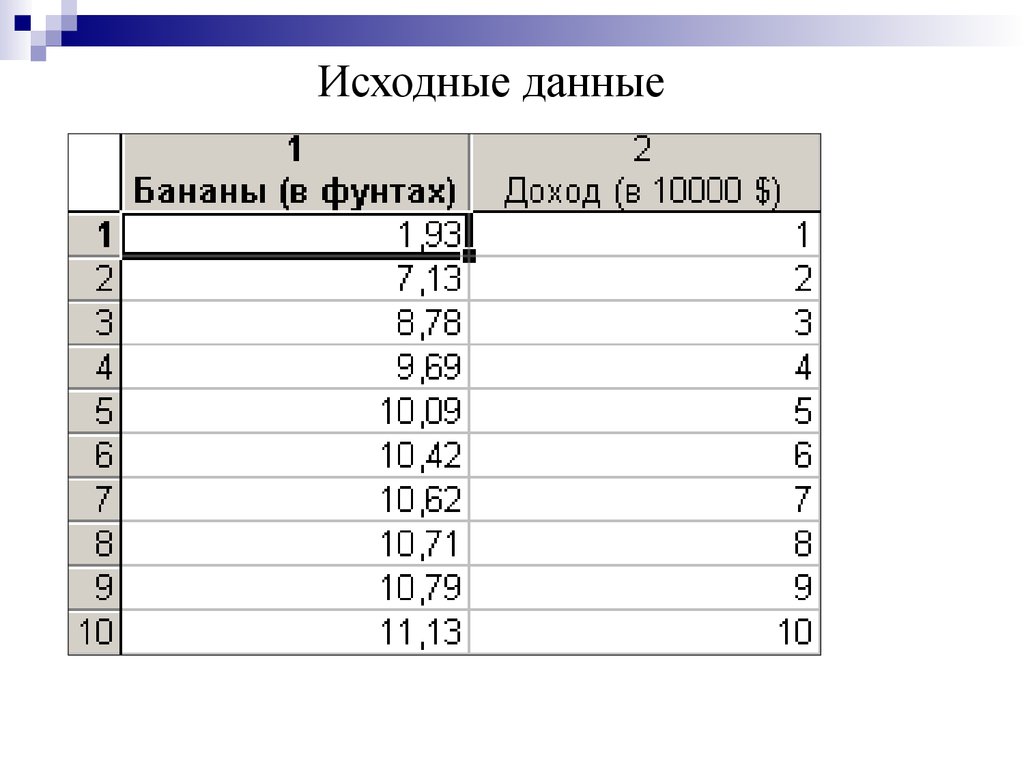
Результативный признак:
Y – Потребление бананов в год (в фунтах)
Факторный признак:
X – Семейный доход (в 10000 $)
26.
Исходные данные27.
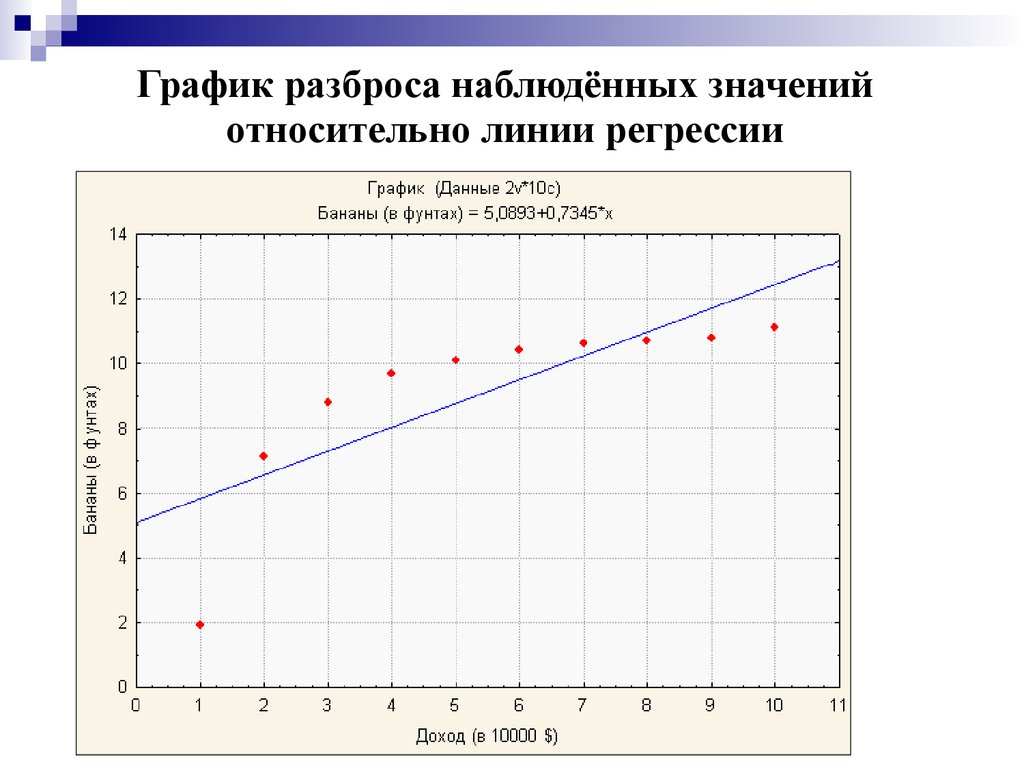
Оценка функции регрессииy 5,089 0,734 x
1, 23
Fнабл 13,786
0.198
2
R 0,637
Fkp 0,05;1;8 5,317
28.
График разброса наблюдённых значенийотносительно линии регрессии
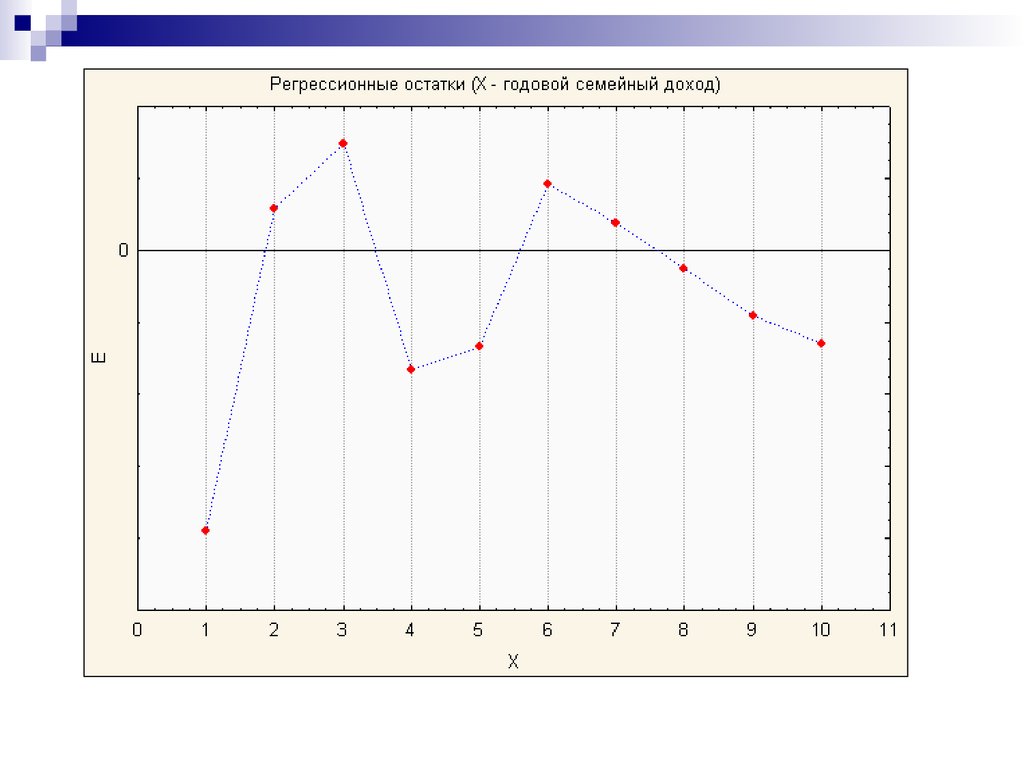
29.
30.
Вычисление статистики Дарбина-УотсонаN
D
e e
i 2
i 1
i
N
2
e
i 1
2
i
Dнабл 0,866
DL 1,08
DU 1,36
31. Рекламная пауза
Контрольная работаУ группы Р06-201 – 30 марта
У группы Р06-203-204 – 25 марта
У группы Р06-205 – 6 апреля
У группы Р06-206 – 30 марта
32. Дополнительные тесты Тест серий (Runs test [Geary test])
Серия–
последовательность
подряд
идущих
регрессионных остатков одного знака (даже единичной
длины). Длина серии – количество элементов серии.
Количество серий являтся случайной величиной со своим
математическим ожиданием (средним числом серий) и
дисперсией.
При отрицательной автокорреляции количество серий
будет велико, а при положительной – слишком мало.
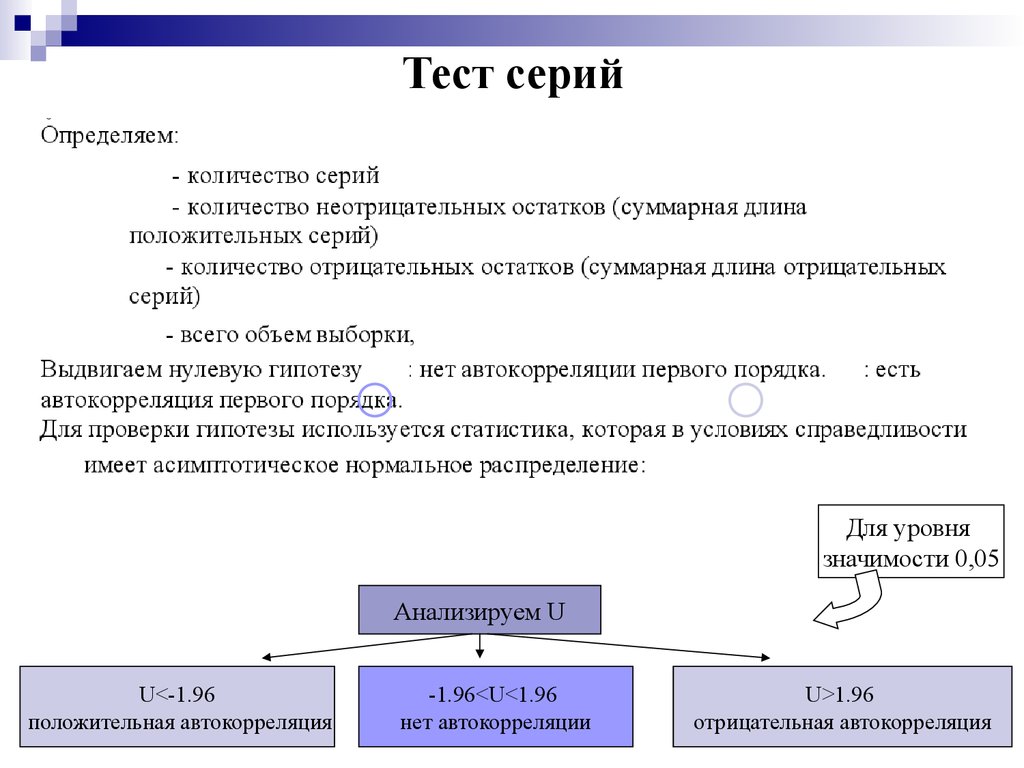
33. Тест серий
Для уровнязначимости 0,05
Анализируем U
U<-1.96
положительная автокорреляция
-1.96<U<1.96
нет автокорреляции
U>1.96
отрицательная автокорреляция
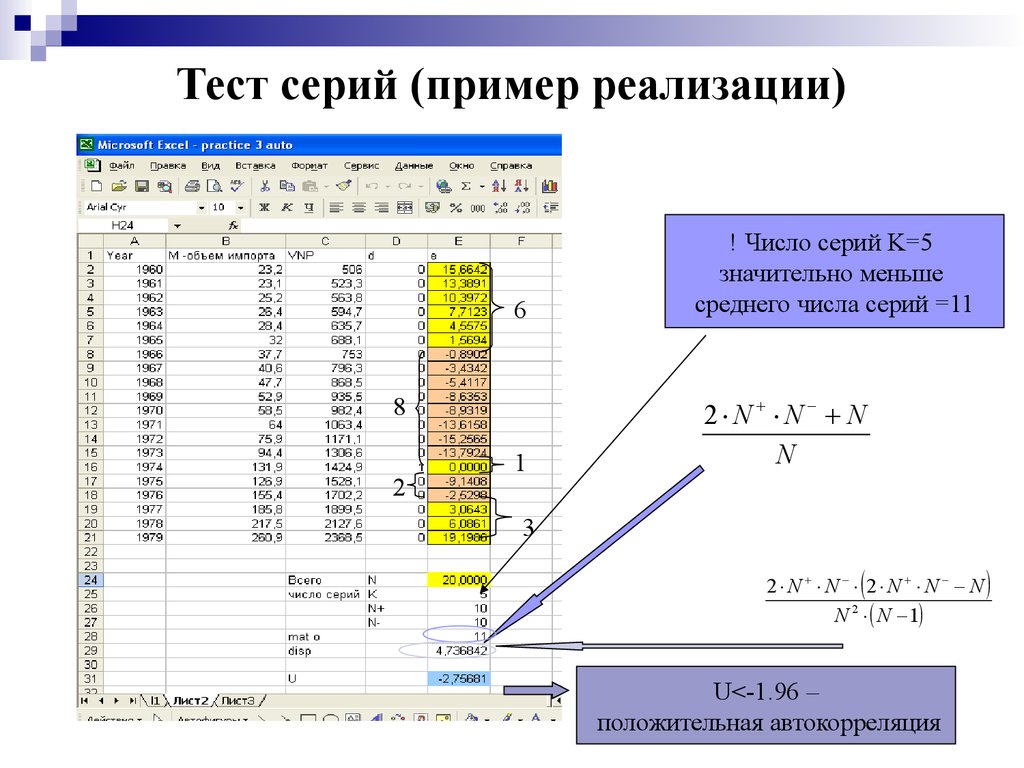
34. Тест серий (пример реализации)
68
2
1
! Число серий K=5
значительно меньше
среднего числа серий =11
2 N N N
N
3
2 N N 2 N N N
N 2 N 1
U<-1.96 –
положительная автокорреляция
35. Дополнительные тесты Общий тест Бройша-Годфри
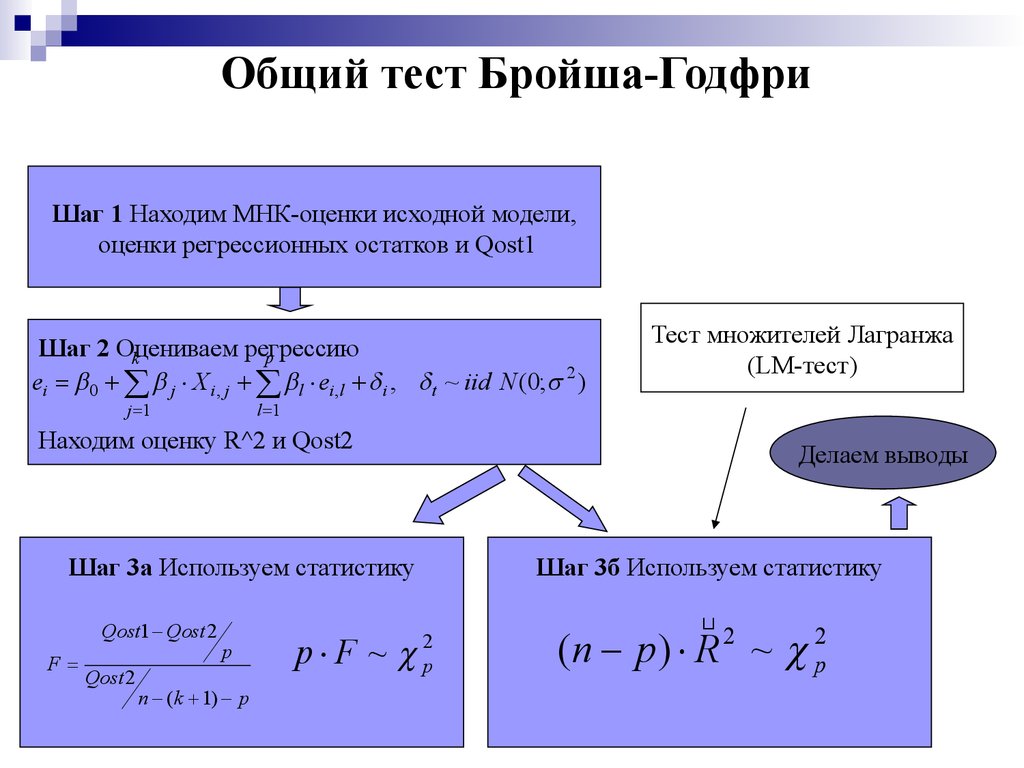
36. Общий тест Бройша-Годфри
Шаг 1 Находим МНК-оценки исходной модели,оценки регрессионных остатков и Qost1
Шаг 2 Оцениваем
регрессию
p
k
ei 0 j X i , j l ei ,l i , t ~ iid N (0; 2 )
j 1
l 1
Находим оценку R^2 и Qost2
Делаем выводы
Шаг 3а Используем статистику
Qost1 Qost 2
F
Qost 2
Тест множителей Лагранжа
(LM-тест)
p
n (k 1) p
p F ~
Шаг 3б Используем статистику
2
p
2
(n p) R ~ p2
37. Методы устранения автокорреляции
Процедура Кохрейна-Оркатта38. Методы устранения автокорреляции
автокорреляцииМетоды
устранения
одим оценку модели регрессии: Y X мнк ;
Процедура
Кохрейна-Оркатта
льзуя построенную
оценку модели
регрессии, находим оценку ве
ионных остатков:
e Y Y Y X мнк
одим оценку неизвестного параметра из оценки моде
ррелированными остатками:
еi еi 1 i , i 2,3,...n
1
е1
е2
...
е
п 1
Т
е1
е2
...
е
п 1
1
е1
е2
...
е
п 1
Т
е2
е3
...
е
п
n
е e
i
i 2
n 1
2
e
i
i 1
i 1
39. Методы устранения автокорреляции
Процедура Кохрейна-Оркатта40. Методы устранения автокорреляции
Процедура Кохрейна-Оркатта41. Методы устранения автокорреляции
Процедура Кохрейна-Оркатта1) находим оценку модели регрессии: Y X мнк ;
2) используя построенную оценку модели регрессии, находим оценку вектора
регрессионных остатков:
e Y Y Y X мнк
3) находим оценку неизвестного параметра из оценки модели с
автокоррелированными остатками:
еi еi 1 i , i 2,3,...n
1
е1 Т е1
е2 е 2
... ...
е е
п 1 п 1
1
е1
е2
...
е
п 1
Т
е2
е3
...
е
п
n
е e
i 1
i
i 2
n 1
e
i 1
2
i
42.
4) Определяем1
0
1 (1) (1) 2 ... (1) п 1
(1)
(1)
(1) п 2
1
...
..........
........
(1) п 1 (1) п 2 ... 1
5) Находим оценку
1
1
Используя вектор омнк , находим оценку e Y Y Y X oмнк
Далее рассчитывается второе приближение и т.д., пока два
соседних приближения не совпадут с определенной степенью
точности.
(1) 1
T
омнк X ( 0 ) X
1
(1) 1
X ( 0 ) Y .
T
43. Точечный прогноз для условного среднего и индивидуального значений результативного признака
44.
При работе с пространственной статистическойинформацией, наличие автокоррелированных
регрессионных остатков, как правило, обусловлено
неправильной спецификацией модели.
Поэтому в некоторых практических задачах методом
устранения автокорреляции является изменение
спецификации (вида функции) регрессионной модели
45.
Изменение спецификации модели как методустранения автокорреляции
Построим функцию регрессии в следующей форме
b1
~
y b0
x
y 12,08 10,08 z
0,05
0.12
1
zi
xi
2
R 0,998

























![Дополнительные тесты Тест серий (Runs test [Geary test]) Дополнительные тесты Тест серий (Runs test [Geary test])](https://cf.ppt-online.org/files/slide/n/nbEICVQDZkXc0xgJK59YzmLq7Hp4FBwaSPsfdM/slide-31.jpg)










 Математика
Математика Экономика
Экономика








