Похожие презентации:
Модель множественной линейной регрессии
1. МОДЕЛЬ МНОЖЕСТВЕННОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
y a1 x1 a2 x2ar 1 xr 1 ar
y – зависимая или объясняемая переменная
x1 , x2
, xr 1
- независимые или объясняющие переменные
- случайная составляющая.
Задача множественного регрессионного анализа – оценить
a1 , a2
ar
2. Пример: Множественная регрессия
Мы хотим определить связь между потреблением, доходомсемьи, финансовыми активами семьи и размером семьи.
• y – потребительские расходы.
• x1 – доход семьи
• x2 – финансовые активы семьи
• x3 – размер семьи
y a1 x1 a2 x2 a3 x3 a4
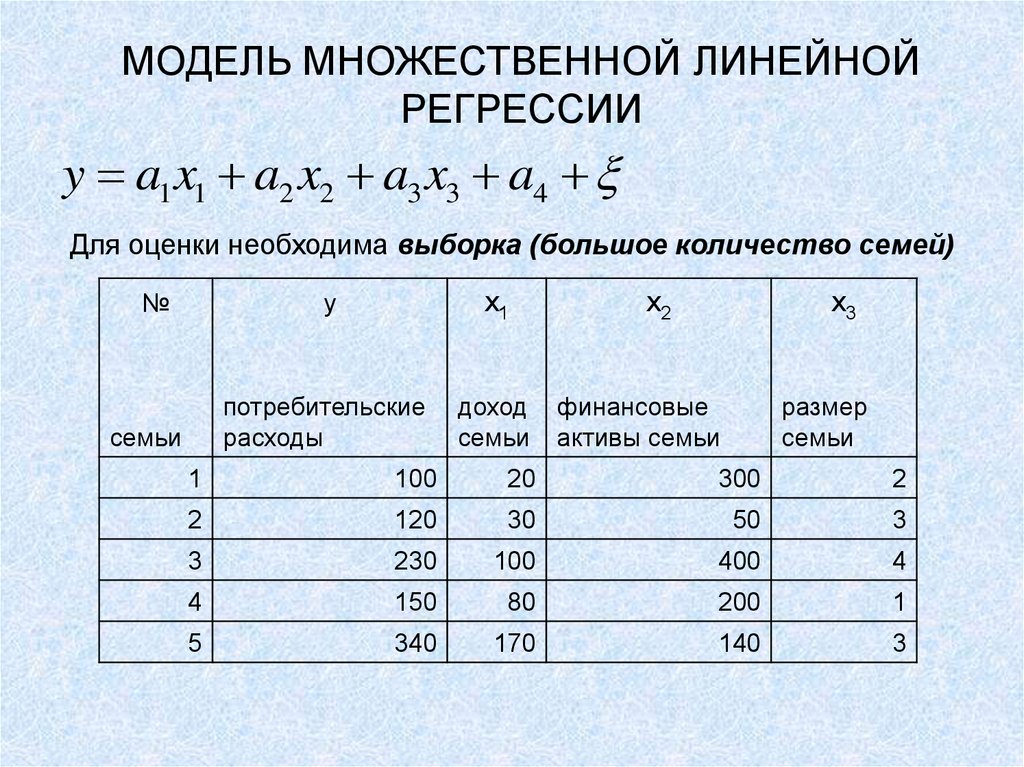
3. МОДЕЛЬ МНОЖЕСТВЕННОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
y a1 x1 a2 x2 a3 x3 a4Для оценки необходима выборка (большое количество семей)
№
семьи
y
x1
потребительские
расходы
доход
семьи
x2
x3
финансовые
активы семьи
размер
семьи
1
100
20
300
2
2
120
30
50
3
3
230
100
400
4
4
150
80
200
1
5
340
170
140
3
4.
n – объем выборкиyi
xi1
xi 2
доходы i-й семьи
xi 3
размер i-й семьи
потребительские расходы i-й семьи
доход i-й семьи
i 1 n
4
5.
Уравнение для i-й семьиyi a1 xi1 a2 xi 2 a3 xi 3 a4 i
Чтобы подобрать наилучшие a , a , a , a
1
2
3
4
n
S (a1 , a2 , a3 , a4 ) yi a1 xi1 a2 xi 2 a3 xi 3 a4
2
i 1
min S (a1 , a2
a1 , a2
ar
ar )
5
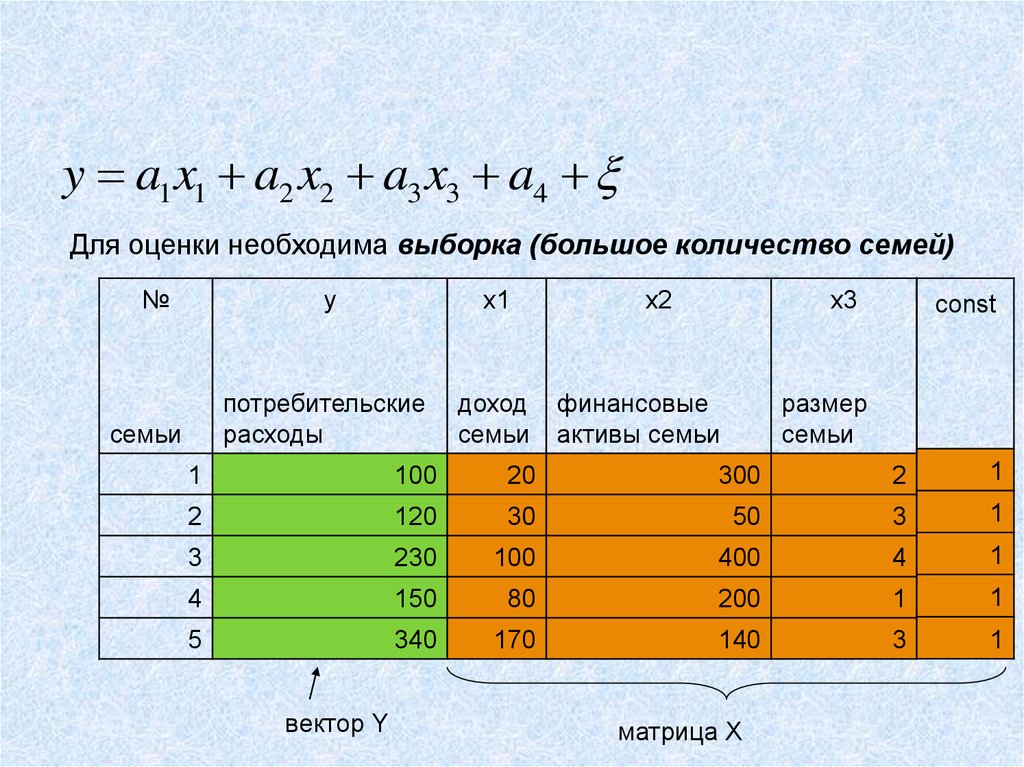
6.
y a1 x1 a2 x2 a3 x3 a4Для оценки необходима выборка (большое количество семей)
№
семьи
y
x1
потребительские
расходы
доход
семьи
x2
x3
финансовые
активы семьи
const
размер
семьи
1
100
20
300
2
1
2
120
30
50
3
1
3
230
100
400
4
1
4
150
80
200
1
1
5
340
170
140
3
1
вектор Y
матрица Х
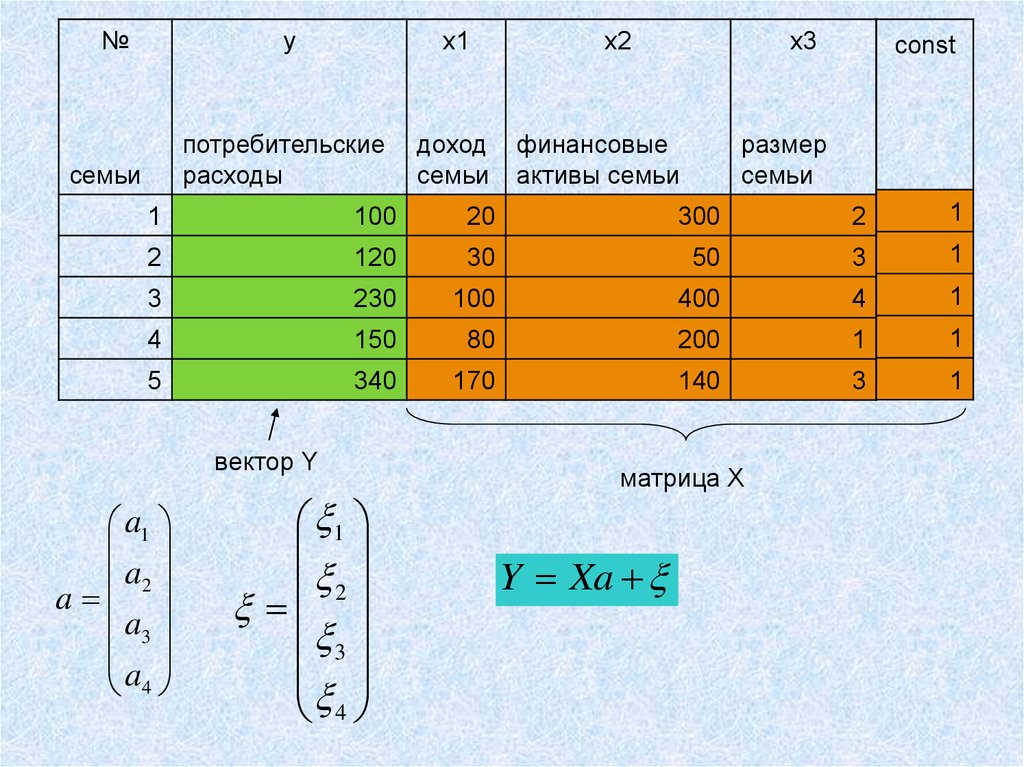
7.
№семьи
y
x1
потребительские
расходы
доход
семьи
x2
x3
финансовые
активы семьи
const
размер
семьи
1
100
20
300
2
1
2
120
30
50
3
1
3
230
100
400
4
1
4
150
80
200
1
1
5
340
170
140
3
1
вектор Y
a1
a2
a
a3
a4
1
2
3
4
матрица Х
Y Xa
8.
Оценки наименьших квадратов (ОНК) вКЛММР
n
S (a1 , a2 , a3 , a4 ) yi a1 xi1 a2 xi 2 a3 xi 3 a4
2
i 1
min S (a1 , a2
a1 , a2
ar
a X X X TY
T
ar )
1
оценка наименьших квадратов (ОНК)
параметров линейной множественной
регрессии
8
9.
№семьи
y
x1
потребительские
расходы
доход
семьи
x2
x3
финансовые
активы семьи
const
размер
семьи
1
100
20
300
2
1
2
120
30
50
3
1
3
230
100
400
4
1
4
150
80
200
1
1
5
340
170
140
3
1
вектор Y
a X X X TY
T
1
матрица Х
10. Пример оценки параметров в модели зависимости заработной платы от числа лет обучения и опыта работы
Коэффициенты
Стандартна
я ошибка
tстатист
ика
PЗначение
Y-пересечение
-26,93164811
4,523407834
-5,95384
4,73E-09
N
2,674036105
0,231999296
11,52605
1,28E-27
0,59409725
0,137923673
4,307435
1,96E-05
Nrab
Zpl = 2.67*N + 0.59*NRab -26.93
10
11.
3D Scatterplot (1 9v*541c)Function = 2,67*x + 0,59*y -26,93
40
20
0
11
12. Условия Гаусса-Маркова для модели линейной множественной регрессии
yi a1 xi1 a2 xi 2Y Xa
1. M i 0
ar 1 xir 1 ar i
i 1, n
i 1, n
На самом деле это требование несущественно,
если в модель включена константа
13.
Условия Гаусса-Маркова для моделилинейной множественной регрессии
yi a1 xi1 a2 xi 2
Y Xa
2
i 1, n
D
2.
i
ar 1 xir 1 ar i
i 1, n
условие гомоскедастичности
(постоянства дисперсии)
14.
Условия Гаусса-Маркова для моделилинейной множественной регрессии
yi a1 xi1 a2 xi 2
Y Xa
3. cov i , j 0
ar 1 xir 1 ar i
i j
i 1, n
автокорреляция
отсутствует
15.
Условия Гаусса-Маркова для моделилинейной множественной регрессии
yi a1 xi1 a2 xi 2
Y Xa
4.
Случайные ошибки
переменных x , x
1
2
ar 1 xir 1 ar i
i
, xr 1
i 1, n
не зависят от объясняющих
16.
Условия Гаусса-Маркова для моделилинейной множественной регрессии
yi a1 xi1 a2 xi 2
Y Xa
5.
ar 1 xir 1 ar i
i 1, n
n r , rangX r
– число наблюдений больше
числа оцениваемых параметров и все r столбцов матрицы
X линейно независимы.
Для обеспечения статистической надежности должно
выполняться условие: n 3r
17.
Условия Гаусса-МарковаМодель Y Xa , удовлетворяющая условиям 1-5
называется классической линейной моделью
множественной регрессии (КЛММР)
18.
Условия Гаусса-МарковаЕсли к 5-ти условиям добавляют шестое
6) Нормальность ошибок: i
N 0, 2
То модель Y Xa
называется
классической нормальной линейной моделью
множественной регрессии (КНЛММР)
19.
CВОЙСТВА ОЦЕНОК КОЭФФИЦИЕНТОВ вКЛММР (ТЕОРЕМА ГАУССА-МАРКОВА)
В КЛАССИЧЕСКОЙ ЛИНЕЙНОЙ МОДЕЛИ МНОЖЕСТВЕННОЙ
РЕГРЕССИИ (выполнены 5 условий Гаусса-Маркова) ОЦЕНКИ
НАИМЕНЬШИХ КВАДРАТОВ
a X X X Y
T
1
T
ЯВЛЯЮТСЯ НЕСМЕЩЕННЫМИ , СОСТОЯТЕЛЬНЫМИ,
ЭФФЕКТИВНЫМИ
Если модель является нормальной (выполнены 6 условий
Гаусса-Маркова), то оценки наименьших квадратов имеют
нормальное распределение. Это позволяет проверять гипотезы и
строить прогнозы с заданным уровнем надежности.
20. ИНТЕРПРЕТАЦИЯ ПАРАМЕТРОВ ЛИНЕЙНОЙ МНОЖЕСТВЕННОЙ РЕГРЕССИИ
y a1 x1 a2 x2ar 1 xr 1 ar
Интерпретация: коэффициент регрессии при переменной xi
показывает на сколько единиц изменится переменная y при
изменении переменной xi на 1 единицу, при условии
постоянства других переменных:
21. Пример оценки параметров в модели зависимости заработной платы от числа лет обучения и опыта работы
Коэффициенты
Стандартна
я ошибка
tстатист
ика
PЗначение
Y-пересечение
-26,93164811
4,523407834
-5,95384
4,73E-09
N
2,674036105
0,231999296
11,52605
1,28E-27
0,59409725
0,137923673
4,307435
1,96E-05
Nrab
Zpl = 2.67*N + 0.59*NRab -26.93
21
22. Пример оценки параметров в модели зависимости заработной платы от числа лет обучения и опыта работы
Коэффициенты
Стандартна
я ошибка
tстатист
ика
PЗначение
Y-пересечение
-26,93164811
4,523407834
-5,95384
4,73E-09
N
2,674036105
0,231999296
11,52605
1,28E-27
0,59409725
0,137923673
4,307435
1,96E-05
Nrab
Zpl = 2.67*N + 0.59*NRab -26.93
Каждый дополнительный год обучения при данном опыте работы увеличивает
часовой заработок на 2,67$
Каждый дополнительный год опыта работы при данной продолжительности
обучения увеличивает часовой заработок на 0,59$
-26,93 не имеет содержательной интерпретации.
22
23. ИНТЕРПРЕТАЦИЯ ПАРАМЕТРОВ ЛИНЕЙНОЙ МНОЖЕСТВЕННОЙ РЕГРЕССИИ
Пример y – затраты на питание (млрд. $)x1 – личный располагаемый доход (млрд. $)
x2 – индекс цен на продукты питания (%)
y 0,112 x1 0,739 x2 116,7
24. ИНТЕРПРЕТАЦИЯ ПАРАМЕТРОВ ЛИНЕЙНОЙ МНОЖЕСТВЕННОЙ РЕГРЕССИИ
Пример y – затраты на питание (млрд. $)x1 – личный располагаемый доход (млрд. $)
x2 – индекс цен на продукты питания (%)
y 0,112 x1 0,739 x2 116,7
При увеличении личного располагаемого дохода на 1 млрд. $ (при
сохранении неизменной цены) расходы на питание увеличатся на
112 млн.$
При увеличении индекса цен на 1 процентный пункт (при сохранении
постоянных доходов) расходы на питание сократятся на 739 млн.$
116,7 не интерпретируется, т.к. x1 и x2 не могут быть равными 0.
25.
Сравнение влияния на зависимую переменнуюразличных объясняющих переменных
Пример y – затраты на питание (млрд. $)
x1 – личный располагаемый доход (млрд. $)
x2 – индекс цен на продукты питания (%)
y 0,112 x1 0,739 x2 116,7
При увеличении личного располагаемого дохода на 1 млрд. $ (при
сохранении неизменной цены) расходы на питание увеличатся на
112 млн.$
При увеличении индекса цен на 1 процентный пункт (при сохранении
постоянных доходов) расходы на питание сократятся на 739 млн.$
116,7 не интерпретируется, т.к. x1 и x2 не могут быть равными 0.
Какой фактор (доход или цена) оказывают большее влияние на расходы на
питание?
26.
Сравнение влияния на зависимую переменнуюразличных объясняющих переменных
Расчет средних эластичностей
Ej aj
xj
y
Средняя эластичность j-го фактора. Показывает на сколько %
изменится среднее значение фактора y при увеличении среднего
значения фактора xj
на 1% от среднего значения
27.
Сравнение влияния на зависимую переменнуюразличных объясняющих переменных
Пример y – затраты на питание (млрд. $)
x1 – личный располагаемый доход (млрд. $)
x2 – индекс цен на продукты питания (%)
y 0,112 x1 0,739 x2 116,7
y 128 ì ëðä$ x1 780 ì ëðä$ x2 120
28.
Сравнение влияния на зависимую переменнуюразличных объясняющих переменных
Пример y – затраты на питание (млрд. $)
x1 – личный располагаемый доход (млрд. $)
x2 – индекс цен на продукты питания (%)
y 0,112 x1 0,739 x2 116,7
y 128 ì ëðä$ x1 780 ì ëðä$ x2 120
780
E1 0,112
0, 68
128
120
E2 0, 739
0, 69
128



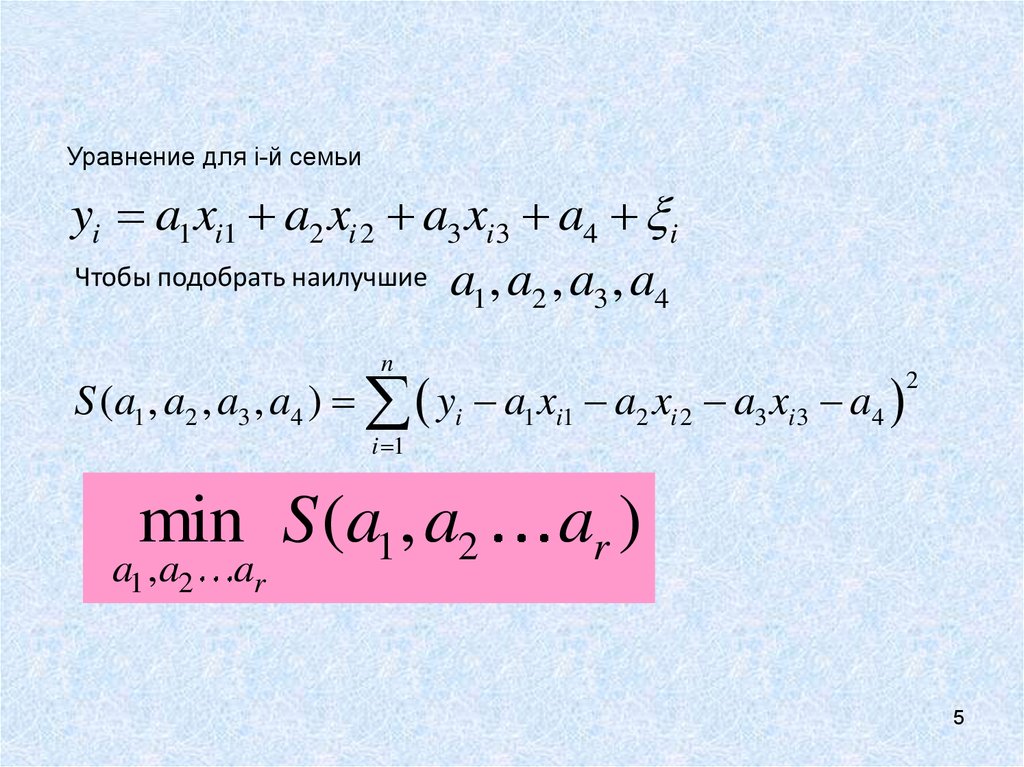





















 Математика
Математика








