Похожие презентации:
Излучение систем источников. Лекция № 8. АФУ
1.
Антенно-фидерные устройства ираспространение радиоволн
ОСНОВЫ ТЕОРИИ АНТЕНН
ЛЕКЦИЯ № 8
2.
Излучение систем источников.8.1. Решетки излучателей.
Для
формирования
остронаправленного
излучения необходимо применять антенну, размеры
которой много больше длины волны. Одной из таких
антенн является система излучателей, между которыми
распределяется подводимая от генератора мощность.
Поля излучения этих источников интерферируют в
пространстве, в одних направлениях суммарное поле
усиливается, в других ослабляется. Результирующая
ДН зависит от расположения излучателей в
пространстве, а также от амплитуд и фаз токов в этих
источниках. Различают непрерывные и дискретные
системы излучателей. Непрерывной называют систему,
в которой излучатели размещены непрерывно вдоль
линии, поверхности или в объёме.
3.
Группаизлучателей,
расположенных
на
некотором расстоянии друг от друга образуют
дискретную систему, называемую антенной решёткой.
Элементом антенной решётки могут быть как один
излучатель, например, симметричный вибратор,
щелевая антенна, диэлектрические и спиральные
антенны, так и сложные антенны, которые сами
являются антенными решётками.
Антенные решётки по способу расположения
излучателей делятся на линейные, поверхностные,
объёмные.
4.
aв
б
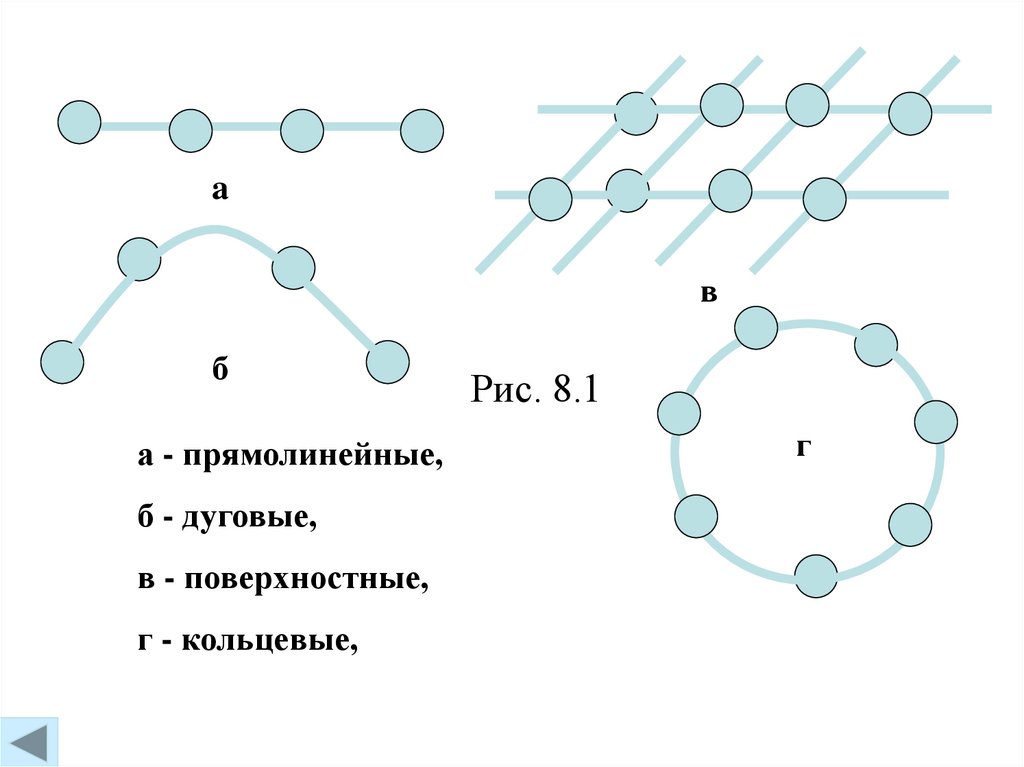
а - прямолинейные,
б - дуговые,
в - поверхностные,
г - кольцевые,
Рис. 8.1
г
5.
дд - цилиндрические,
Рис. 8.2
е
е - сферические,
6.
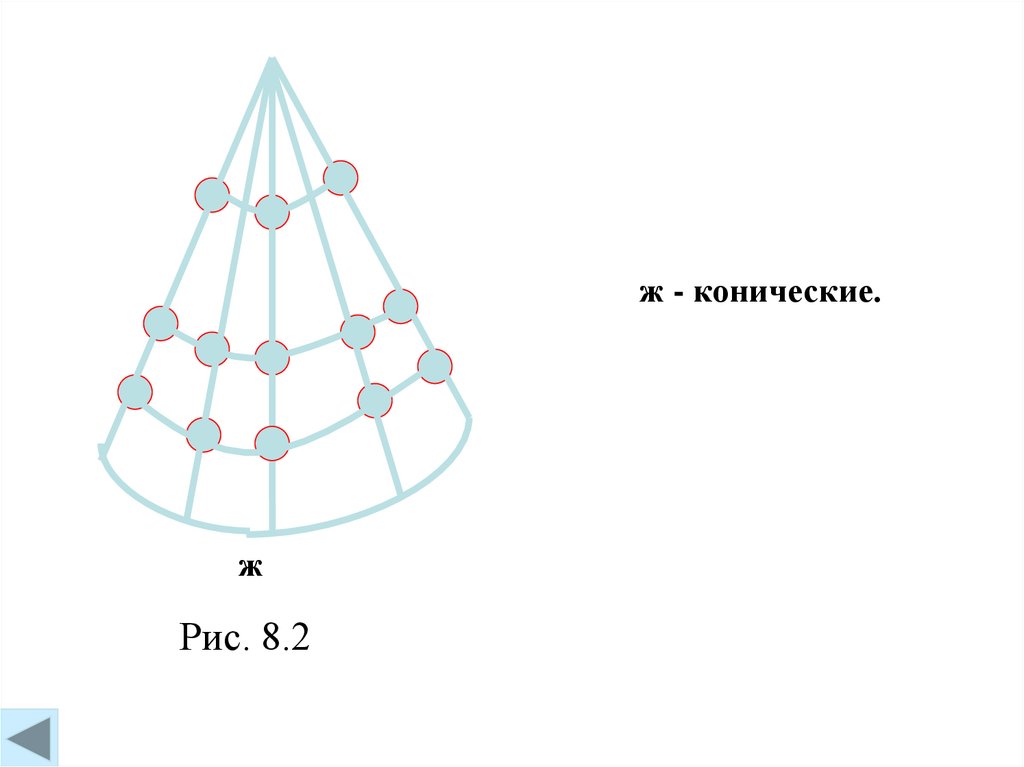
ж - конические.ж
Рис. 8.2
7.
Решётки бывают эквидистантными когдарасстояние
между
соседними
излучателями
одинаково.
Линейно-фазные решётки - это решётки, в
которых фазы токов изменяются по линейному
закону.
Если фазы токов в излучателях одинаковы, то
антенная решётка называется синфазной.
8.
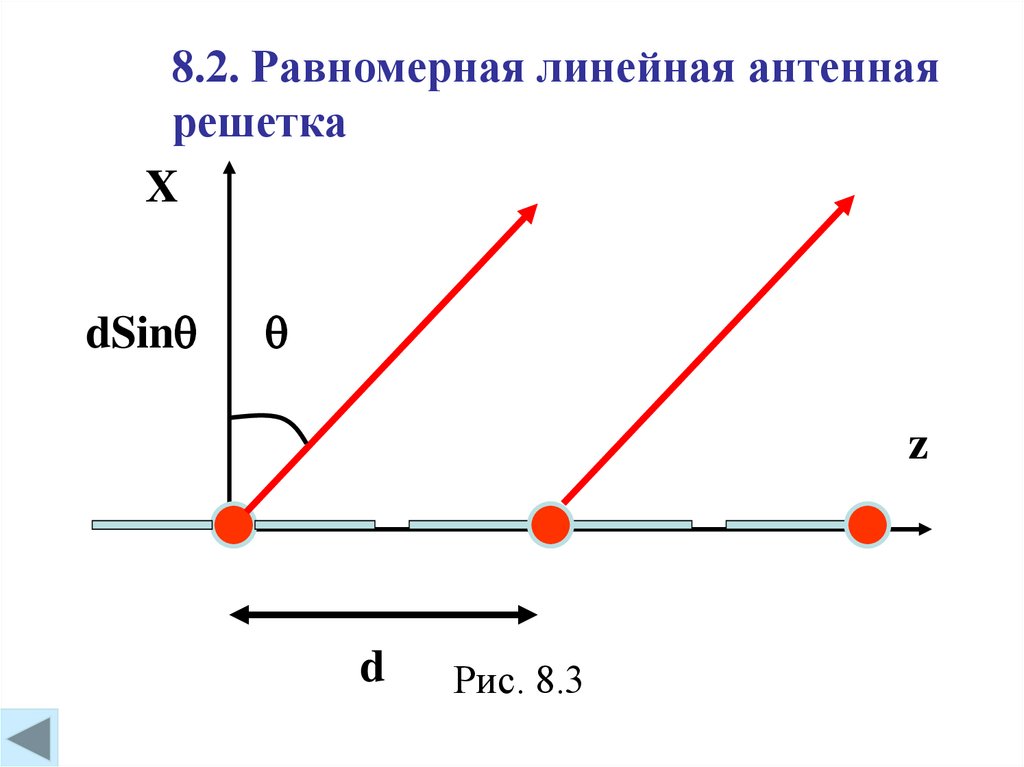
8.2. Равномерная линейная антеннаярешетка
X
dSin
z
d
Рис. 8.3
9.
Считаем:1) Излучателями являются симметричные вибраторы.
2) Токи в излучателях одинаковы по амплитуде.
3) Фаза тока в каждом последующем излучателе
отстаёт от фазы тока в предыдущем на , т. е.
изменяется по линейному закону. Т. е. имеем
равноамплитудную, линейно-фазную, прямолинейную
решётку.
4) Точка наблюдения находится на расстоянии r >> d,
тогда направления на точку наблюдения от всех
излучателей будут параллельными.
Найдём результирующее поле в дальней зоне:
10.
E2 = E1 exp [i(kdSin - )](8.1)
где - угол между нормалью к оси решетки и точкой
наблюдения;
kdSin - пространственный сдвиг фаз между полями
соседних излучателей.
Решётка состоит из n - элементов. Тогда поле n-го
элемента:
En = E1 exp [i(n-1)(kdSin - )]
11.
Поле первого излучателя:60 I n Cos(klSin ) Coskl
E1 i
*
r
Cos
(8.2)
exp(
ikr
)
*
Результирующее поле:
E=E1+E2+ ... + En=
= E1{1+ei(kdSin - )+…+ei(n-1)(kdSin - )} (8.3)
(8.3) - геометрическая прогрессия.
12.
p nE E1 exp i( p 1)( kdSin )
(8.4)
p 1
Если I1 I2 In, то:
p n
E E1
p 1
Ip
I
exp i ( p 1)( kdSin )
(8.5)
13.
Сумма геометрической прогрессии:q 1
E E1
q 1
n
in ( kdSin )
e
1
= E1 i ( kdSin )
e
1
(8.6)
14.
q - знаменатель прогрессии.Делаем преобразование:
in( kdSin ) / 2
e
E E1 i ( kdSin ) / 2 *
e
in( kdSin ) / 2
in( kdSin ) / 2
e
e
* i ( kdSin ) / 2 i ( kdSin ) / 2
e
e
(8.7)
15.
E E1ei ( n 1) u
inu
e e
iu
iu
e e
inu
(8.8)
Тогда результирующее поле в дальней зоне:
60 I n Cos(klSin ) Coskl
E i
*
r
Cos
Sin{n (kdSin )} i ( n 1)u ( ikr )
2
e
e
*
Sin{ 1 (kdSin )}
2
(8.9)
16.
Полученное соотношение запишем в виде:E=AF1( , )Fc( , )ei ( )e-ikr,
где A=60In/r - амплитудный множитель;
F1( , )
характеристика
направленности
симметричного вибратора;
Fc( , ) - множитель системы,
( ) - фазовая характеристика направленности
антенны.
Множитель
системы
характеристика
направленности линейной системы, состоящей из n
ненаправленных излучателей, расположенных и
возбуждённых также, как и реальные излучатели.
17.
Характеристикарешётки:
направленности
антенной
F1( , )Fc( , )ei ( ) = F( , )
Окончательно:
60 I n Cos(klSin ) Coskl
E i
*
r
Cos
Sin{n (kdSin )}
2
(8.10)
*
Sin{ 1 (kdSin )}
2
18.
Максимальное значение результирующее поля:Emax= nE1
Множитель системы равен:
Sin{n (kdSin )}
2
(8.11)
Fc
nSin{ 1 (kdSin )}
2
19.
F( , )-B
0
Рис. 8.4
B
20.
Вывод:1) Направление главных лепестков определяется
из условия: u = 2m , m = 0, 1, 2, … - порядок
лепестка.
2) Направление боковых лепестков u = (2m+1) /n,
m=1, 2 , 3, ...
3) Направления, в которых излучение отсутствует
(нули ДН) u = 2m /n (m = pn, p - целое число).
21.
8.3. Синфазная антенная решеткаn
Sin{ kdSin }
2
E E1
Sin{ 1 kdSin }
2
Диаграмма направленности:
(8.12)
E
Cos(klSin ) Coskl
F ( )
*
Emax
Cos
Sin{n kdSin }
2
*
nSin{ 1 (kdSin }
2
(8.13)
22.
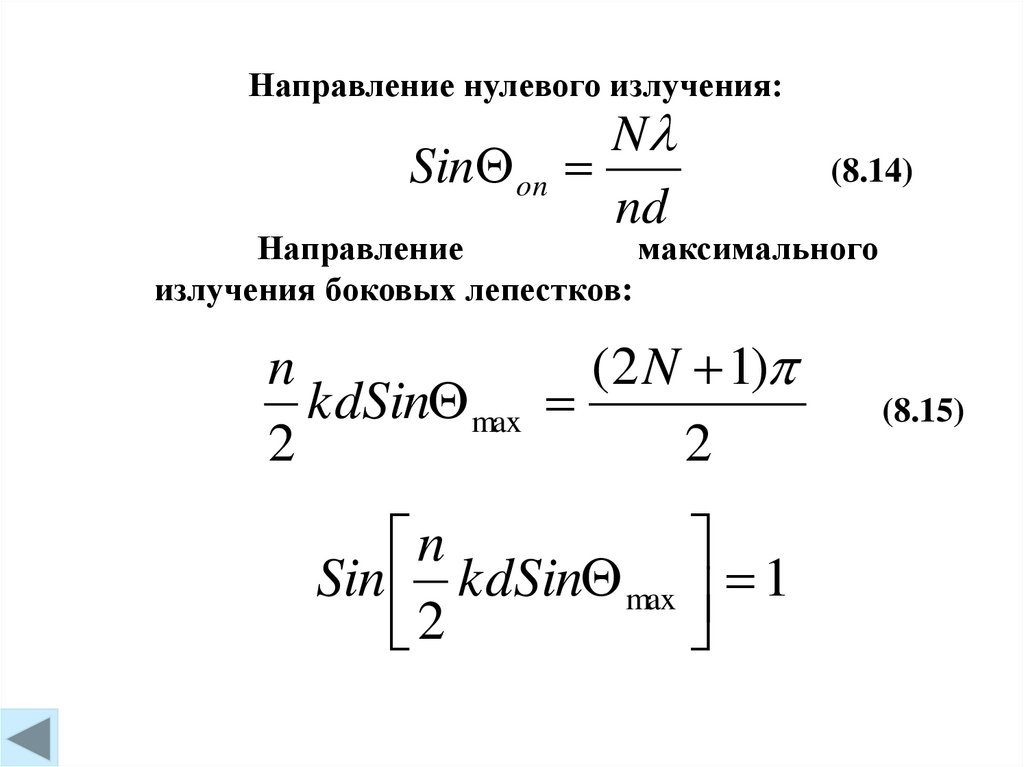
Направление нулевого излучения:N
Sin on
nd
(8.14)
Направление
максимального
излучения боковых лепестков:
n
(2 N 1)
kdSin max
2
2
n
Sin kdSin max 1
2
(8.15)
23.
Направление первого нулевого излучения:Sin 0
(8.16)
nd
d - шаг решётки.
При /nd << 1, ширина главного лепестка:
2
2 0
nd
[рад]
24.
Диаграмма направленности:0
180
Рис. 8.5
25.
Уровень боковых лепестков.Направление максимума:
Sin max N
2N 1
2 nd
Максимум излучения бокового лепестка:
Emax
E1
(2 N 1)
Sin
2
2
(8.17)
26.
Уровень бокового лепестка:1
n
2N 1
nSin (
)
n 2
1
n
(2 N 1)
При больших L/ :
D
2L
(8.18)
(8.19)











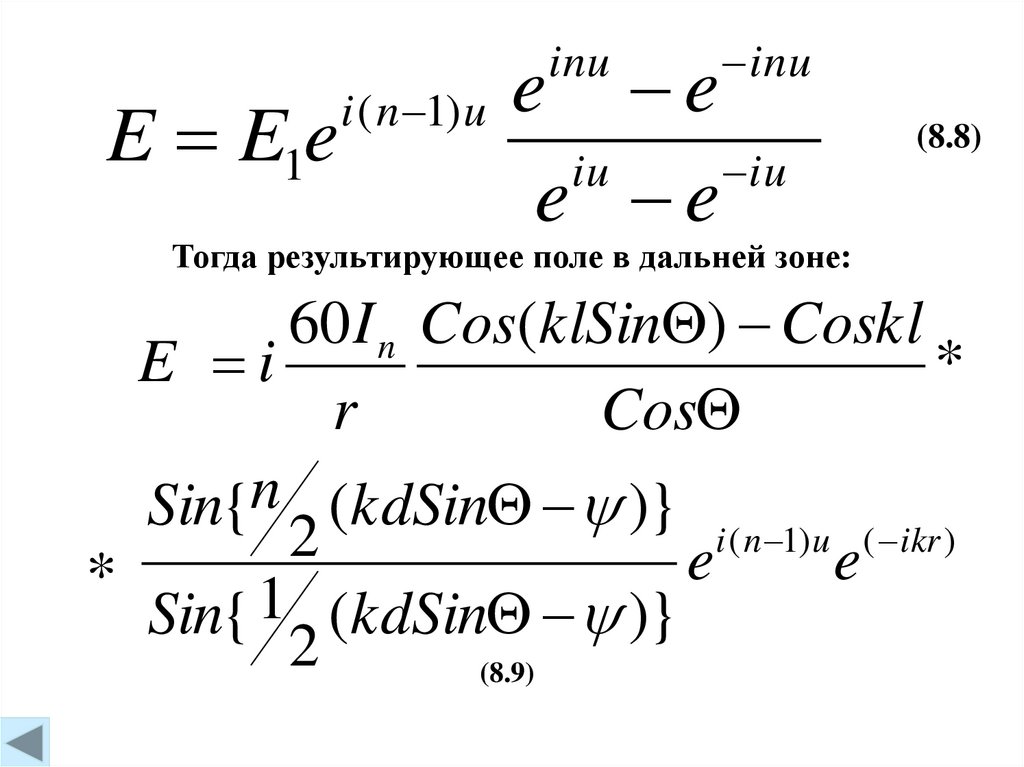














 Физика
Физика








