Обратная задача магниторазведки

1. Обратная задача магниторазведки

2.

Геологическая интерпретация геофизических данных –
извлечение геологической информации из геофизических
данных
Интерпретация магнитных аномалий подразделяется на:
•качественную
•количественную

3. Условия, определяющие адекватное решение обратной задачи

1. В классе 2D-моделей решение выполняется по
данным графика магнитной аномалии по профилю
2. Необходимо определение модели геологического
объекта по форме наблюденного графика магнитного
поля
3. Обратная задача решается для магнитного поля
изолированного тела, с допущением однородной
намагниченности объекта по всему объему

4.

Обратная задача – это вычисление элементов залегания и
физических свойств искомых геологических объектов по
значениям наблюденного магнитного поля,
удовлетворяющих имеющейся априорной информации
глубина
геометрия
магнитные свойства

5. Методы решения обратной задачи

1. Метод характерных точек
• метод касательных
• метод «полумаксимума»
2. Дифференциальные
3. Интегральные
4. Векторные
5. Подбора

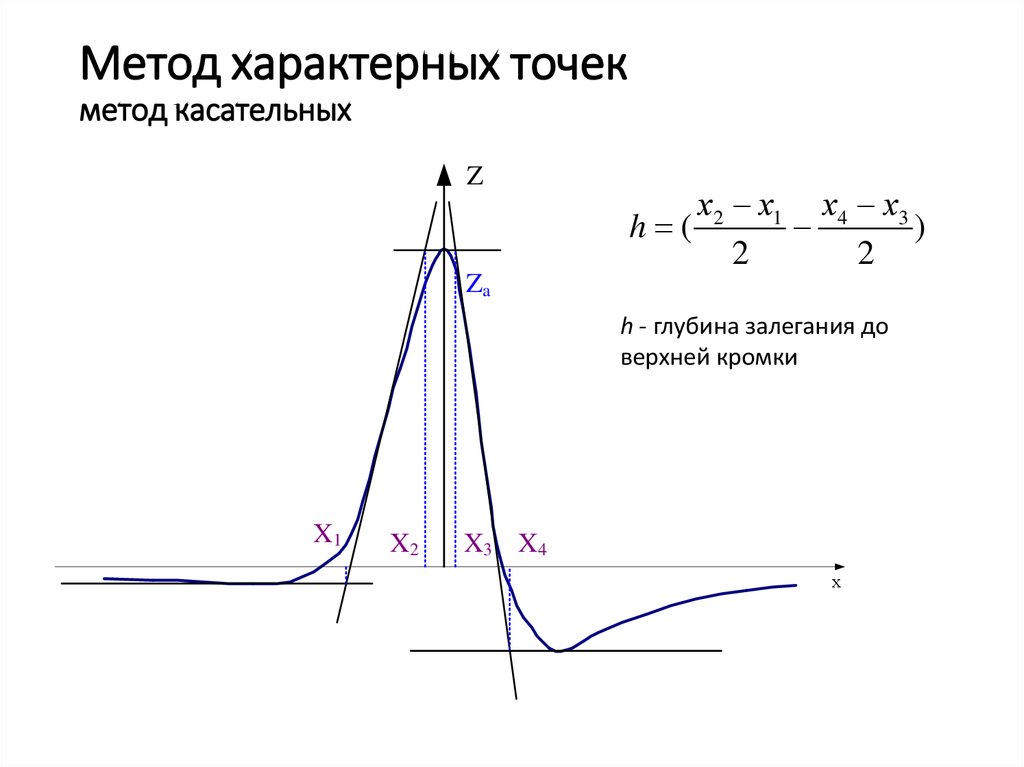
6. Метод характерных точек метод касательных

Z
h (
х2 х1 х4 х3
)
2
2
Za
h - глубина залегания до
верхней кромки
X1
X2
X3 X4
х

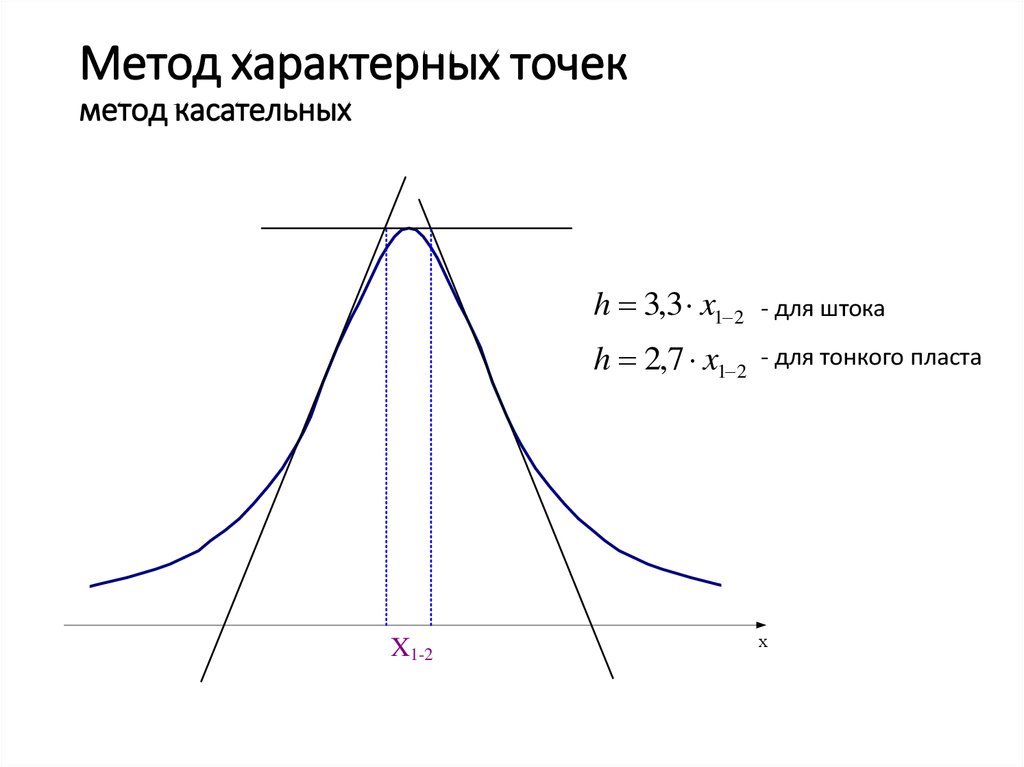
7. Метод характерных точек метод касательных

X1-2
h 3,3 x1 2
- для штока
h 2,7 x1 2
- для тонкого пласта
х

8. Метод характерных точек метод «полумаксимумов»

Za
Zп
Zmax
Xmin
X0
Xп Xmax X1/2
Zmin
x

9. Метод характерных точек метод «полумаксимумов»: обозначения

xmax
xmin
xext
xп
X0
x1/2
x1/4
расстояние по
профилю от начала
координат до
2xmax
2xmin
2xext
2x0
2x1/2
2x1/4
расстояние между
соседними точками
максимума
минимума
экстремума
перегиба
перехода через 0
полумаксимума
четверти
максимума
максимумов
минимумов
экстремумов
перехода через 0
полумаксимумов
полуминимумов

10. Метод характерных точек метод «полумаксимумов»

1. Шар (диполь)
h 0,5 xmin
1
М Z max h 3
2
h 0,707 x0
2. Горизонтальный цилиндр бесконечного простирания
h x0
h 2x1 / 2
М
1
Z max h 2
2
3. Вертикальный пласт бесконечной глубины
4.
x12/ 4 x12/ 2
h
2x1 / 2
b x12/ 2 h 2
2
xmin
x02
h
2x0
l x h
J
Z max
b
Вертикальный пласт ограниченной глубины h
4arctg
2
0
2
1
М Z max (h 2 l 2 )
2

11. Метод характерных точек метод «полумаксимумов»

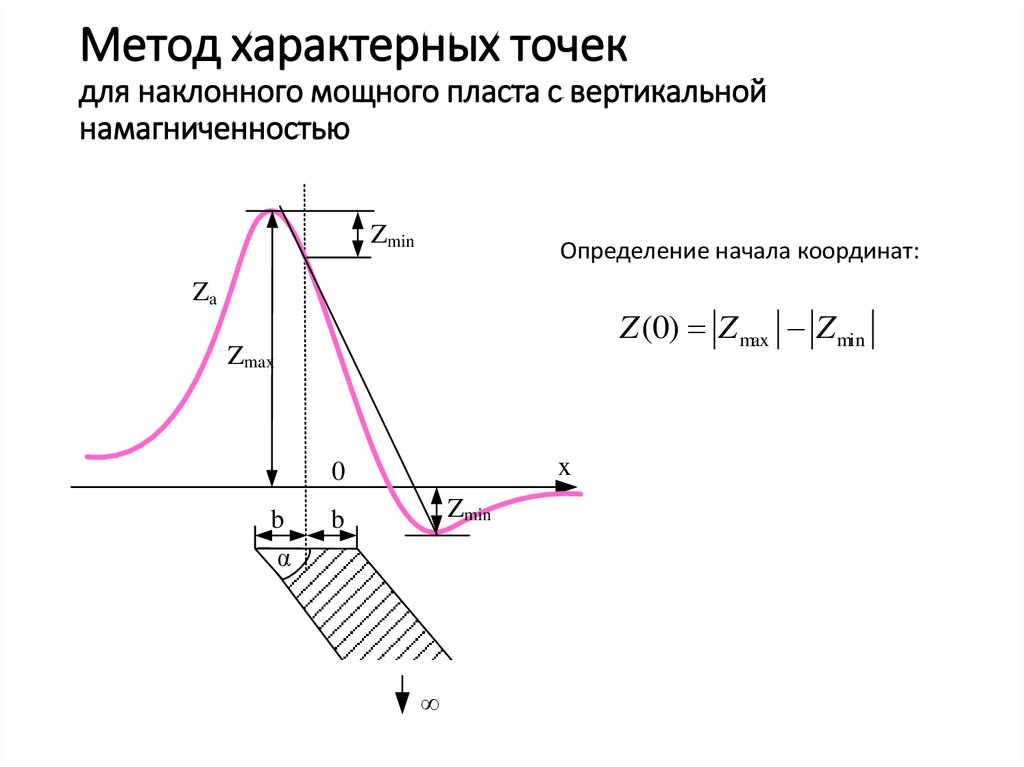
12. Метод характерных точек для наклонного мощного пласта с вертикальной намагниченностью

Zmin
Определение начала координат:
Za
Z (0) Z max Z min
Zmax
x
0
b
α
Zmin
b
∞

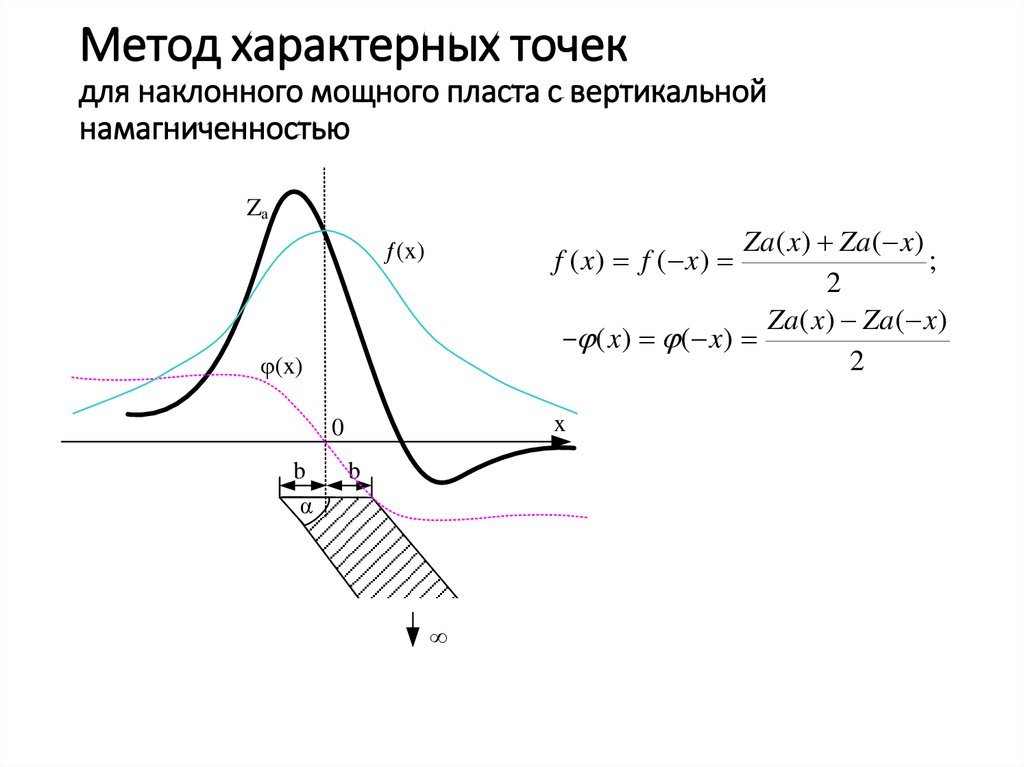
13. Метод характерных точек для наклонного мощного пласта с вертикальной намагниченностью

Za
Za ( x) Za( x)
;
2
Za( x) Za( x)
– ( x) ( x)
2
ƒ(x)
f ( x) f ( x)
φ(x)
x
0
b
α
b
∞

14. Метод характерных точек для наклонного мощного пласта с вертикальной намагниченностью

x12/ 4 x12/ 2
h
;
2 x1 / 2
b x12/ 2 h 2
2bh
arctg 2
2
2
f ( x)
x
b
h
2tg
( x)
( x b) 2 h 2
ln
x b 2 h 2
Za (0)
1
J
2
2bh sin
2arctg 2
h b2
x1 x2
cos
2 x1 x3
или
Вычисляется по четной функции
Вычисляется угол падения по полученным
данным
1
x1 x3 sin ;
2
1
h x2 x4 sin ;
2
1
h x1 x2 tg
2
h
J
f ( x) max
b
4arctg
h
x x
cos 1 2
2 x2 x4
1
b
2
x2 x1 2 h 2 csc 2
4

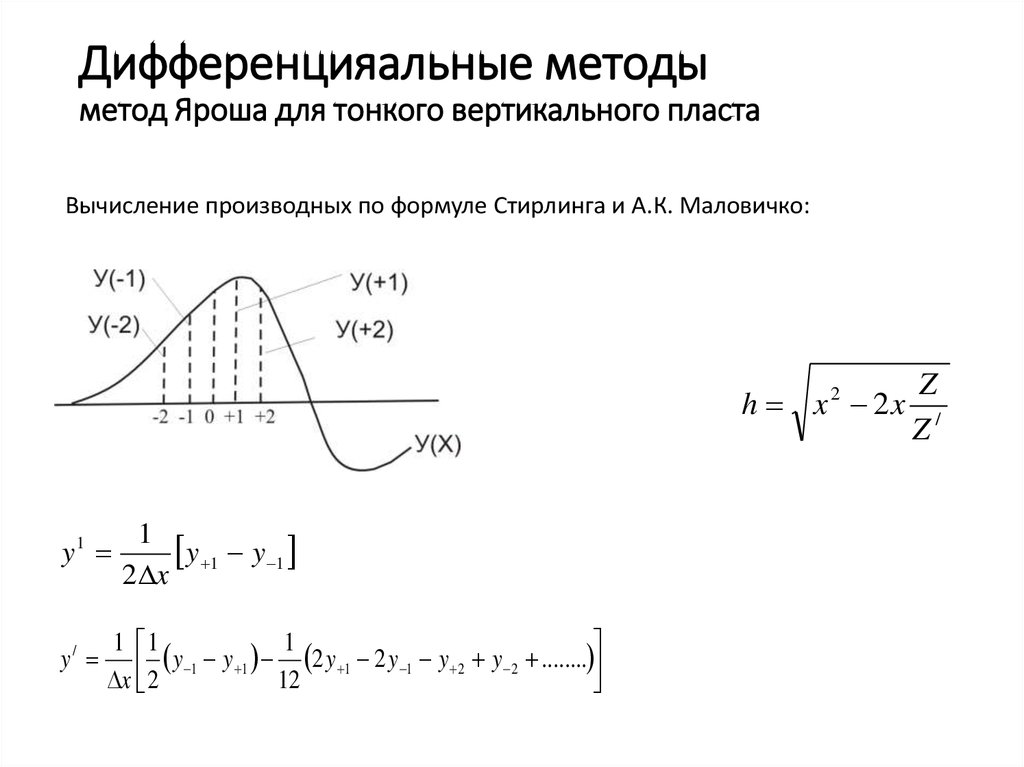
15. Дифференцияальные методы метод Яроша для тонкого вертикального пласта

Вычисление производных по формуле Стирлинга и А.К. Маловичко:
h x 2 2x
y1
y/
1
y 1 y 1
2 x
1 1
1
y
y
2
y
2
y
y
y
........
1
1
1
1
2
2
x 2
12
Z
Z/

16. Интегральные методы

Двухмерные объекты – достаточно провести расчеты по
одному профилю пересекающему тело
•бесконечной глубины
•ограниченной глубины
Трехмерные объекты – расчеты необходимо проводить по
плану изолиний

17. Интегральные методы

S
2b
2 J

18. Векторные методы

Ta
T

19. Метод подбора

Метод подбора – это подбор формы и физических свойств
возмущающего объекта (объектов) путем многократного
решения прямой задачи магниторазведки для выбранного
класса моделей
Корректность задачи предполагает:
•существование решения
•единственность решения
•устойчивость решения

20. Метод подбора корректность задачи по Тихонову

Согласно А.Н. Тихонову, задача считается корректной,
если:
1)априори известно, что ее решение существует для
некоторого класса моделей
2)решение единственно в некотором классе данных
3)бесконечно малым вариациям данных задачи, не
выводящим решение за пределы множества корректности
соответствуют бесконечно малые вариации решения

21. Метод подбора классификация моделей

1. Адекватные – модельное поле с высокой точностью
соответствует наблюденному полю, распределение
физических свойств в изучаемом объеме среды с высокой
точностью соответствует априорным данным
2. Эквивалентные – модельное поле с высокой точностью
соответствует наблюденному полю, распределение
физических свойств в изучаемом объеме среды заведомо
не обеспечивает нужной точности аппроксимации
3. Смешанные – смешанная модель обеспечивает требуемую
близость наблюденного и модельного полей и
аппроксимацию распределения физических свойств части
объема геологической среды, позволяющую решить
целевую задачу интерпретации.

22. Метод подбора среднеквадратичная погрешность подбора

n
2
Z
Z
набл m
i 1
n
где n – количество пунктов наблюдения, Zнабл i – наблюденное поле в iой точке, Zм i – модельное поле в i-ой точке
Точность подбора не должна быть меньше точности съемки!
Высокая точность – ε < 5 нТл
Средняя точность – ε = (5-15) нТл