Что такое эконометрика. Модель парной регрессии

1. ЭКОНОМЕТРИКА ЛИТЕРАТУРА К КУРСУ:

Основная
К.Доугерти
«Введение в эконометрику» , М.: Инфра-М
(пер. под ред. Замкова)
(желательно последнее издание 2007г!!!)

2. ЧТО ТАКОЕ ЭКОНОМЕТРИКА

Экономическая теория
Экономическая статистика
Эконометрика
Микроэкономика
Теория Вероятностей и
математическая статистика
Макроэкономика

3.

Эконометрика
1. Формулирует экономические модели,
основываясь на экономической теории
(микро и макроэкономике)
2. Оценивает неизвестные параметры модели
на базе реальных статистических данных
3. Использует построенные модели для
объяснения поведения исследуемых
экономических показателей,
прогнозирования, а также для
осмысленного проведения экономической
политики.

4. МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ

y – зависимая (объясняемая) переменная
х – независимая (объясняющая) переменная

5. МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ

y – зависимая (объясняемая) переменная
х – независимая (объясняющая) переменная
1. Вычисляем средние значения
1 n
y yi
n i 1
1 n
x xi
n i 1
СРЗНАЧ(диапазон данных)

6. МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ

y – зависимая (объясняемая) переменная
х – независимая (объясняющая) переменная
2. Вычисляем дисперсии
n
1
sx2 ( xi x) 2
n i 1
n
1
s y2 ( yi y ) 2
n i 1
ДИСПР(диапазон данных)

7. МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ

y – зависимая (объясняемая) переменная
х – независимая (объясняющая) переменная
3. Вычисляем ковариацию
1 n
cov( x, y ) ( xi x)( yi y )
n i 1
КОВАР(диапазон данных х, диапазон данных y)

8. МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ

y – зависимая (объясняемая) переменная
х – независимая (объясняющая) переменная
4. Вычисляем корреляцию
co r ( x, y )
cov( x, y )
s s
2
x
2
y
КОРРЕЛ(диапазон данных х, диапазон данных y)

9. МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ

y – зависимая (объясняемая) переменная
х – независимая (объясняющая) переменная
4. Анализируем коэффициент корреляции
Коэффициент корреляции принимает значения от -1 до 1.
Значения близкие к 1 – есть тесная прямая связь между х и у
Значения близкие к -1 – есть тесная обратная связь между х и у
Значения близкие к 0 – связь между х и у отсутствует

10. ПАРНАЯ РЕГРЕССИЯ

Диаграмма рассеяния
350
300
250
y
200
150
100
50
0
-50
-20
0
20
40
60
80
100
120
x
Коэффициент корреляции близок к 1
140
160

11.

Scatterplot (образец графика индикаторов в лог шкале 10v*110c)
y = 2,8502-1,983*x
-10
-12
-14
y
-16
-18
-20
-22
-24
6
7
8
9
10
11
x
Коэффициент корреляции близок к -1
12
13

12.

7
6
y
5
4
3
2
1
-1
0
1
2
3
4
5
6
x
Коэффициент корреляции близок к 0
7

13. МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ

y – зависимая (объясняемая) переменная
х – независимая (объясняющая) переменная
6. Если коэффициент корреляции не близок к 0 строим модель парной
линейной регрессии
y ax b

14. МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ

y ax b
Предположим, что необходимо получить функцию
спроса на некоторый товар в зависимости от
дохода.
Проводится опрос домохозяйств.
1. Среднедушевой доход домохозяйства?
2. Сколько единиц товара приобрело домохозяйство
за месяц?

15. МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ

№
домохозяйства
Среднедушевой доход
домохозяйства, д.е.
Объем спроса, ед.
1
100
24
2
200
42
3
150
35
4
80
24
5
160
39

16. МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ

Спрос (y),ед.
Нанесем точки на график
x
45
40
35
30
25
20
15
10
5
0
0
30
60
90
120
Доход (x), д.е.
150
180
210
y
100
24
200
42
150
35
80
24
160
39

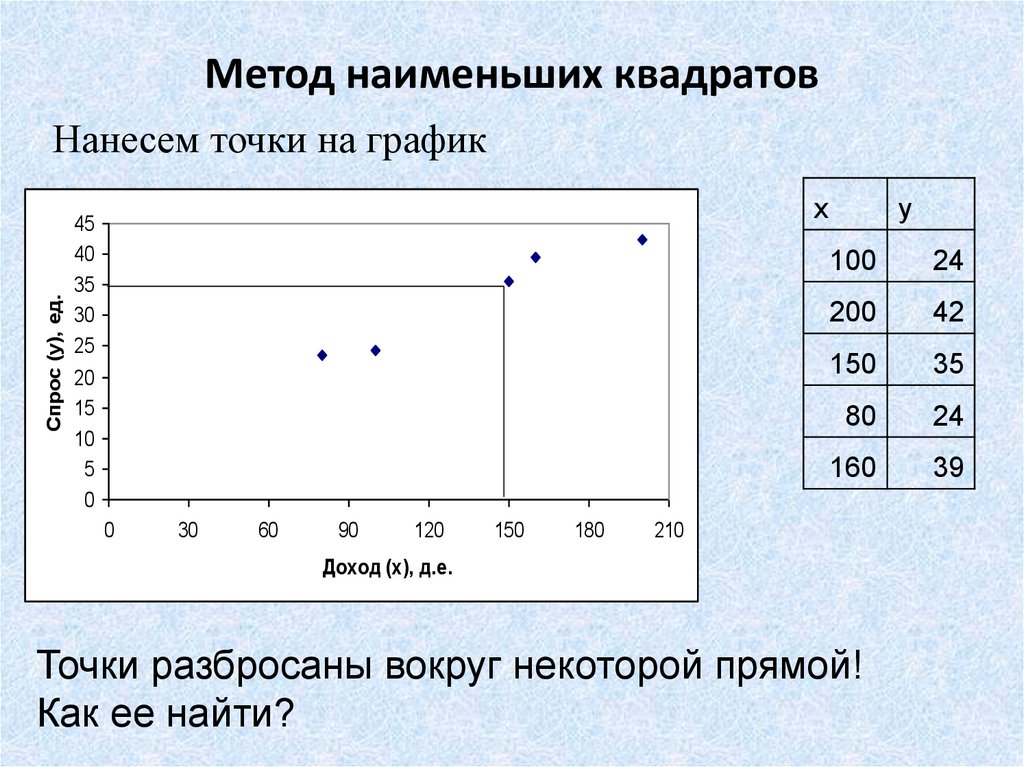
17. Метод наименьших квадратов

Спрос (y), ед.
Нанесем точки на график
x
45
40
35
30
25
20
15
10
5
0
0
30
60
90
120
150
180
y
100
24
200
42
150
35
80
24
160
39
210
Доход (x), д.е.
Точки разбросаны вокруг некоторой прямой!
Как ее найти?

18. Метод наименьших квадратов

Спрос (y), ед.
Нанесем точки на график
x
45
40
35
30
25
20
15
10
5
0
0
30
60
90
120
150
180
y
100
24
200
42
150
35
80
24
160
39
210
Доход (x), д.е.
Расстояние от каждой точки до прямой должно
быть как можно меньше!

19. Метод наименьших квадратов

Спрос (y), ед.
Нанесем точки на график
x
45
40
35
30
25
20
15
10
5
0
0
30
90
60
120
Доход (x), д.е.
Плохая прямая!
150
180
210
y
100
24
200
42
150
35
80
24
160
39

20. Метод наименьших квадратов

Спрос (y), ед.
Нанесем точки на график
x
45
40
35
30
25
20
15
10
5
0
0
30
60
90
120
150
180
y
100
24
200
42
150
35
80
24
160
39
210
Доход (x), д.е.
Хорошая прямая! Но может быть есть еще лучше?

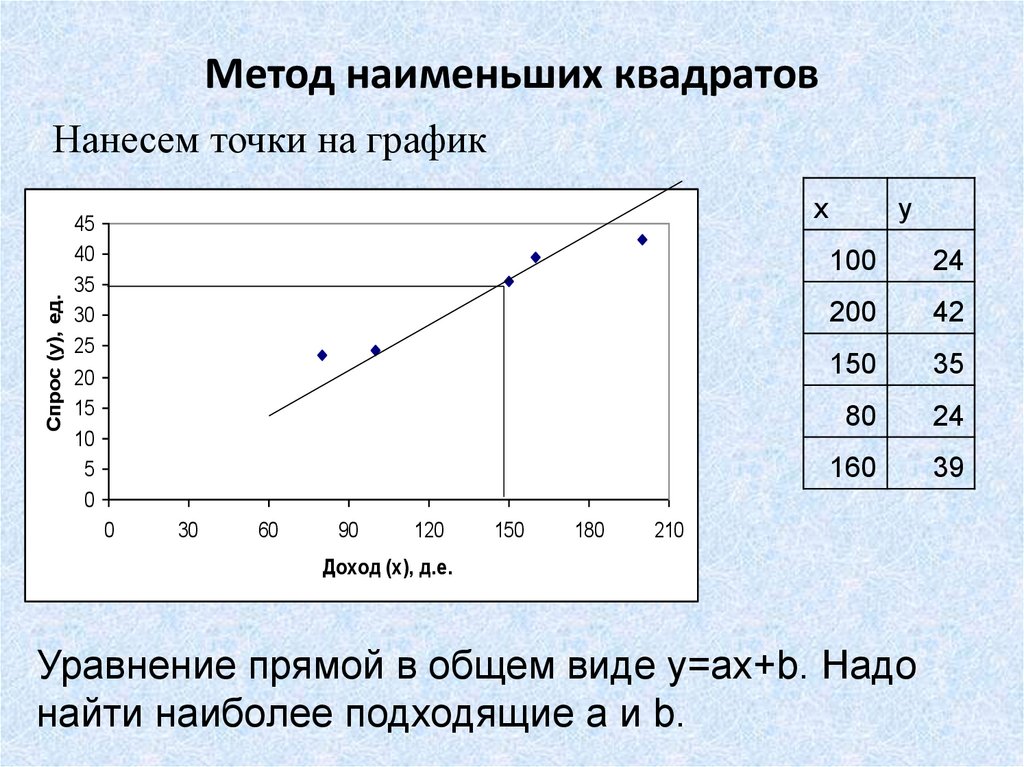
21. Метод наименьших квадратов

Спрос (y), ед.
Нанесем точки на график
x
45
40
35
30
25
20
15
10
5
0
0
30
60
90
120
150
180
y
100
24
200
42
150
35
80
24
160
39
210
Доход (x), д.е.
Уравнение прямой в общем виде y=ax+b. Надо
найти наиболее подходящие a и b.

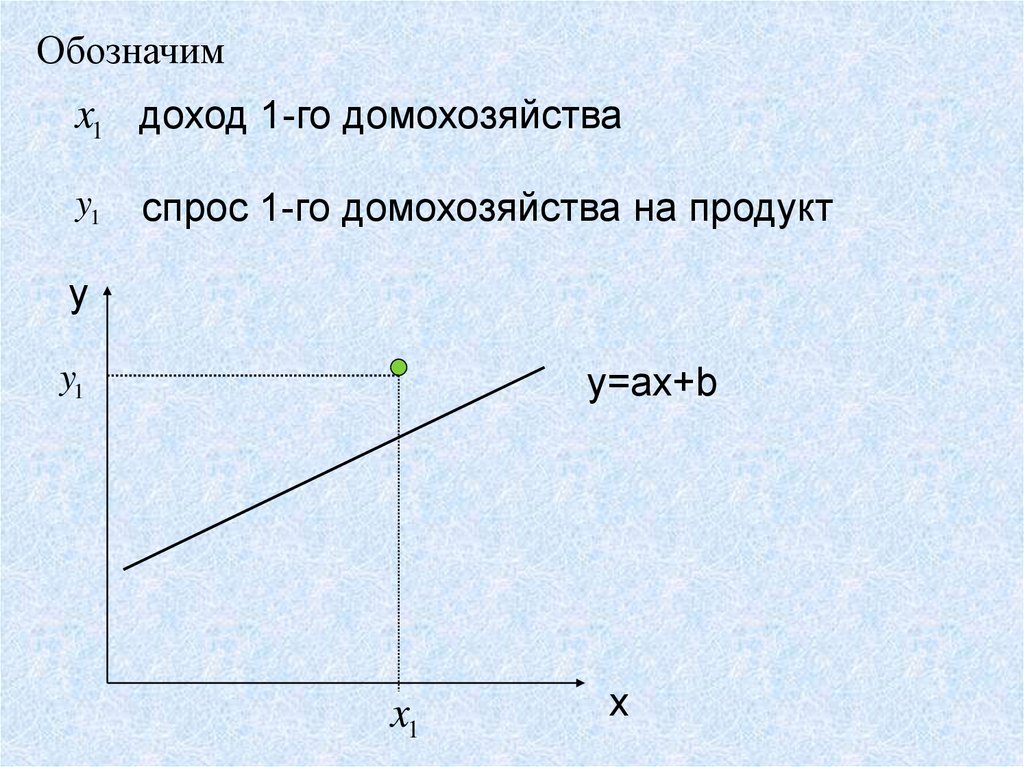
22.

Обозначим
x1 доход 1-го домохозяйства
y1
спрос 1-го домохозяйства на продукт
y
y1
y=ax+b
x1
x

23.

Обозначим
x1 доход 1-го домохозяйства
y1
спрос 1-го домохозяйства на продукт
y
y1
y=ax+b
Отклонение точки
от прямой. Должно быть
как можно меньше!
x1
x

24.

Обозначим
x1 доход 1-го домохозяйства
y1
спрос 1-го домохозяйства на продукт
y
y1
y=ax+b
ax1 b
Отклонение точки
от прямой. Должно быть
как можно меньше!
x1
x
d1 y1 (ax1 b)

25.

А если точка лежит ниже прямой?
Тогда отклонение d (ax b) y
1
1
1
y
y=ax+b
ax1 b
y1
Отклонение точки
от прямой. Должно быть
как можно меньше!
x1
x

26.

Как учесть сразу оба случая?
Квадрат отклонения d 2 ( y (ax b)) 2
1
1
1
должен быть как можно меньше.
y
y=ax+b
ax1 b
y1
Отклонение точки
от прямой. Должно быть
как можно меньше!
x1
x

27.

Квадрат отклонения до второй точки тоже должен
быть как можно меньше.
d 22 ( y2 (ax2 b)) 2 min

28.

Квадрат отклонения до второй точки тоже должен
быть как можно меньше.
d 22 ( y2 (ax2 b)) 2 min
И для третьей точки
d ( y3 (ax3 b)) min
2
3
2

29.

Предположим, что у нас n точек.
Тогда и для последней точки
d n2 ( yn (axn b)) 2 min

30.

Как учесть все точки сразу?
d12 d 22 d32
d n2 min
Сумма квадратов расстояний от точек до прямой
должна быть как можно меньше.

31.

Как учесть все точки сразу?
d12 d 22 d32
d n2 min
Сумма квадратов расстояний от точек до прямой
должна быть как можно меньше.
d d d
2
1
2
2
2
3
n
d d
2
n
i 1
2
i
обозначение

32.

Как учесть все точки сразу?
n
2
d
i min
i 1
n
2
(
y
(
ax
b
))
min
i
i
i 1
n
S (a, b) ( yi axi b)
2
i 1
Получили функцию двух переменных, для которой надо найти минимум,
т.е. надо исследовать на экстремум.

33.

n
S (a, b) ( yi axi b) 2
i 1
xi и yi
это просто числа, нам известные
cov( x, y )
a
2
sx
b y ax

34.

Спрос (y), ед.
Вернемся к примеру
45
40
35
30
25
x
20
15
10
5
0
0
30
60
90
120
Доход (x), д.е.
Надо найти
x, y, sx2 ,cov( x, y)
150
180
210
y
100
24
200
42
150
35
80
24
160
39

35.

Спрос (y), ед.
Вернемся к примеру
45
40
35
30
25
20
15
10
5
0
x
0
30
60
90
120
150
180
210
Доход (x), д.е.
x 138, y 33, sx2 1856,cov( x, y) 315.6
y
100
24
200
42
150
35
80
24
160
39

36.

x 138, y 33, sx2 1856,cov( x, y) 315.6
315.6
a
0.17
1856
b y ax
a=0,17, b=9,33
y=0,17x+9,33 - уравнение прямой, которая
проходит ближе всего к точкам.

37.

Спрос (y), ед.
50
45
40
35
30
25
20
15
10
5
0
y = 0,17x +9,33
0
30
60
90
120
150
180
210
Доход (x), д.е.
y=0,17x+9,33 - функция спроса в зависимости
от дохода.
Интерпретация коэффициента а: при увеличении х на 1 ед. y увеличится на
а единиц.

38.

Коэффицие Стандарт
нты
ная ошибка
tстатисти
ка
P-Значение
Y-пересечение
9,334052
3,296116
2,831833
0,06609
Переменная X 1
0,170043
0,0228
7,458124
0,004991
y=0,17x+9,33 - функция спроса в зависимости
от дохода.

39.

Коэффицие Стандарт
нты
ная ошибка
tстатисти
ка
P-Значение
Y-пересечение
9,334052
3,296116
2,831833
0,06609
Переменная X 1
0,170043
0,0228
7,458124
0,004991
y=0,17x+9,33 - функция спроса в зависимости
от дохода.
С ростом дохода на 1 ден.ед. спрос на товар
растет на 0,17 ед.

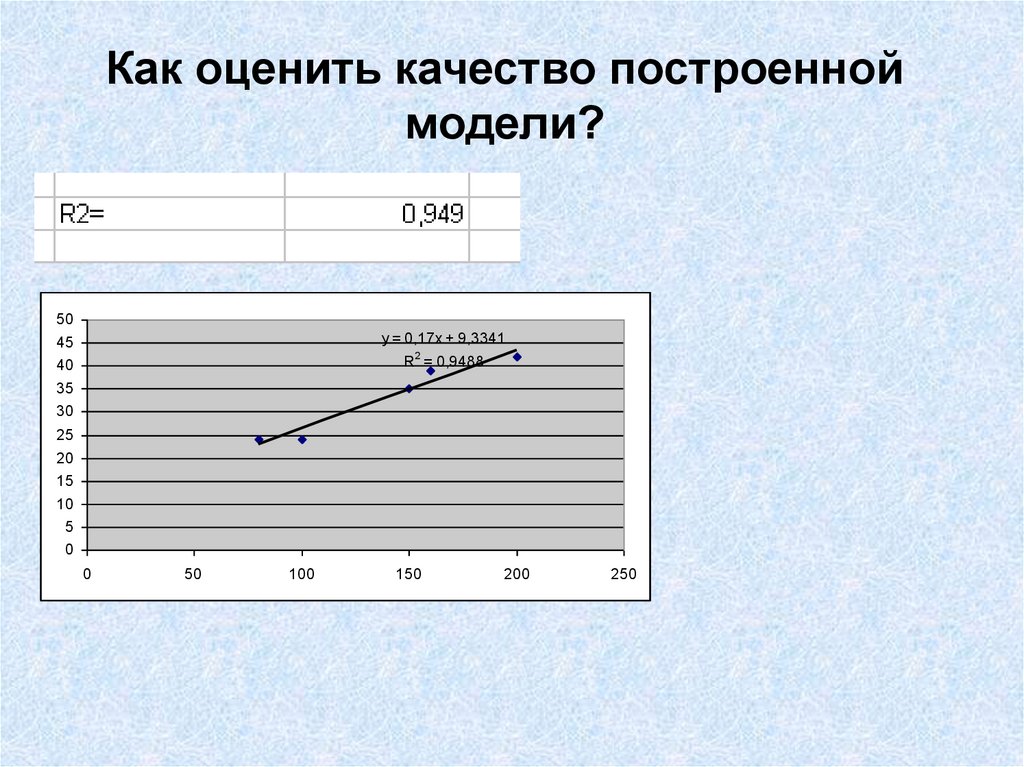
40. Как оценить качество построенной модели?

Построим прогноз по модели по формуле
y 0,17x+9,33

41. Как оценить качество построенной модели?

Вычисляем остатки
e y y

42. Как оценить качество построенной модели?

Находим относительную ошибку аппроксимации
A
y y
y
Процентный формат

43. Как оценить качество построенной модели?

Находим среднюю относительную ошибку аппроксимации
среднее по столбцу
В среднем прогноз отличается от наблюдаемого значения на 4,83%

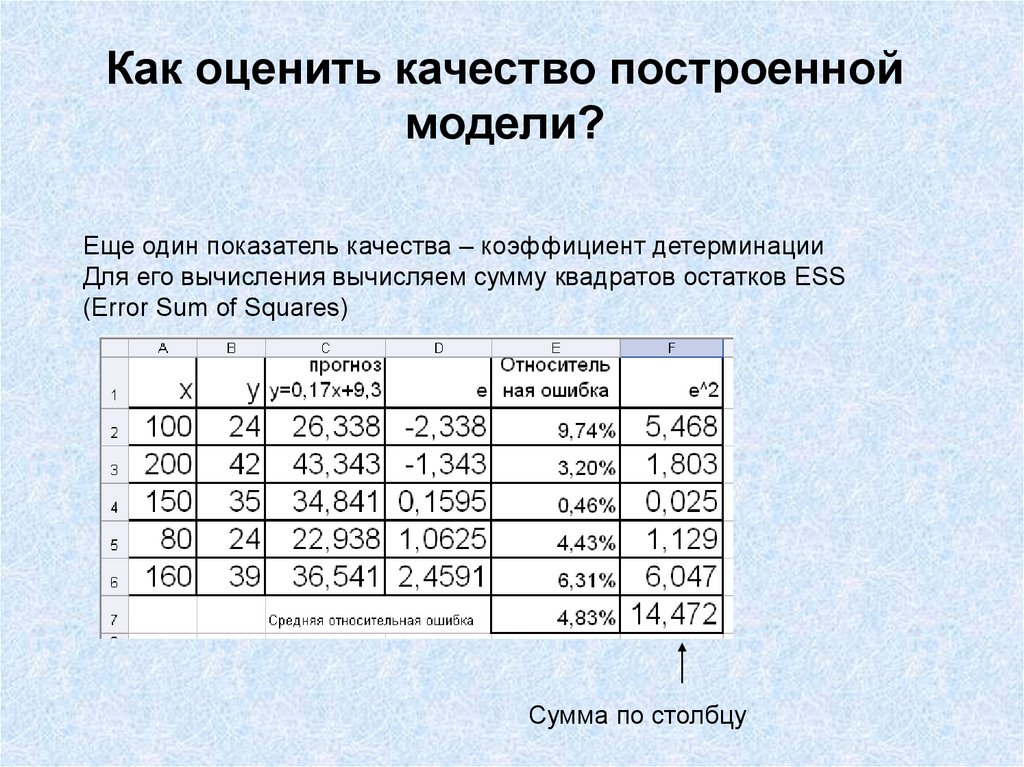
44. Как оценить качество построенной модели?

Еще один показатель качества – коэффициент детерминации
Для его вычисления вычисляем сумму квадратов остатков ESS
(Error Sum of Squares)
Сумма по столбцу

45. Как оценить качество построенной модели?

коэффициент детерминации
ESS
R 1
2
n sy
2

46. Как оценить качество построенной модели?

коэффициент детерминации
ESS
R 1
2
n sy
2
показывает долю вариации зависимой переменной, объясненную
регрессией. Изменяется от 0 до 1
Чем ближе этот показатель к 1, тем лучше качество регрессии

47. Как оценить качество построенной модели?

94,9% вариации спроса на продукт объясняется доходом и остальные 5,1%
прочими факторами, не включенными в модель

48. Как оценить качество построенной модели?

50
y = 0,17x + 9,3341
45
R2 = 0,9488
40
35
30
25
20
15
10
5
0
0
50
100
150
200
250

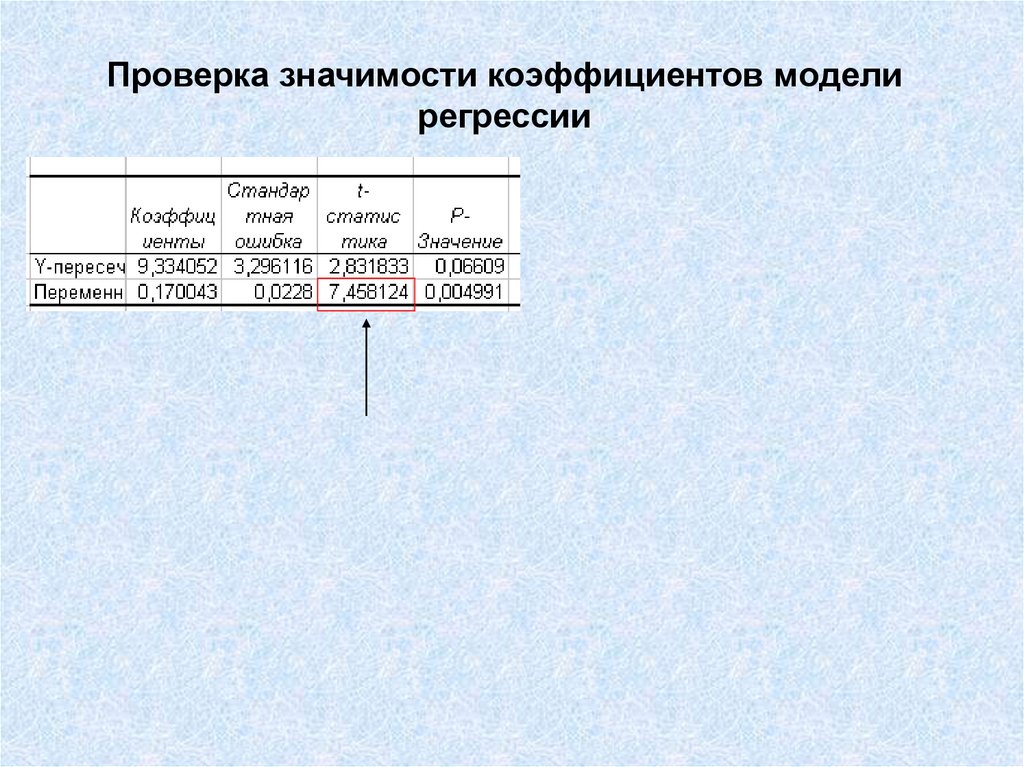
49. Проверка значимости коэффициентов модели регрессии

Построено уравнение
y ax b
Даже если в реальности y не зависит от х, уравнение можно построить.
Но пользоваться им для прогноза нельзя.
В связи с этим проверяют значимость коэффициента a, т.е. насколько
существенно а отличается от 0. Если коэффициент незначим, то переменная
y не зависит от переменной х и моделью нельзя пользоваться

50. Проверка значимости коэффициентов модели регрессии

Построено уравнение
y ax b
Даже если в реальности y не зависит от х, уравнение можно построить.
Но пользоваться им для прогноза нельзя.
В связи с этим проверяют значимость коэффициента a, т.е. насколько
существенно а отличается от 0. Если коэффициент незначим, то переменная
y не зависит от переменной х и моделью нельзя пользоваться
Для проверки значимости коэффициента a рассчитывается величина
a
Ta
sa
s
где,
- стандартная ошибка коэффициента а.
a
Рассчитывается по специальным формулам

51. Проверка значимости коэффициентов модели регрессии

52. Проверка значимости коэффициентов модели регрессии

На основе t-статистики рассчитывают Р-значение
Р-значение - это вероятность того, что переменная х не значима. При Рзначении меньще 0,05 обычно считают, что соответствующая переменная
значима, т.е. y зависит от х
В этом примере переменная х значима, т.е. влияет на переменную y

53.

y=0,17x+9,33 - функция спроса в зависимости
от дохода.
1)Выполнить прогноз потребления продукта
домохозяйством с доходом 200 д.е.
2) Найти среднюю эластичность спроса по
доходу
x
E a
y

54.

y=0,17x+9,33 - функция спроса в зависимости
от дохода.
1)Выполнить прогноз потребления продукта
домохозяйством с доходом 200 д.е.
2) Найти среднюю эластичность спроса по
доходу
x
E a
y

55.

Модели парной нелинейной регрессии

56.

№
домохозяйства
Среднедушевой
доход
Объем спроса, кг в
домохозяйства, месяц
тыс. д.е.
1
1
1,71
2
2
6,88
3
3
8,25
4
4
9,52
5
5
9,81
6
6
11,43
7
7
11,09
8
8
10,87
9
9
12,15
10
10
10,94

57.

14
x
Спрос (y), кг
12
y
10
1
1,71
8
2
6,88
3
8,25
2
4
9,52
0
5
9,81
6
11,43
7
11,09
8
10,87
9
12,15
10
10,94
6
4
0
Доход (x),тыс. д.е.
Зависимость нелинейная!

58.

14
y = 0,8448x + 4,6187
Спрос (y), кг
12
x
y
10
1
1,71
8
2
6,88
3
8,25
2
4
9,52
0
5
9,81
6
11,43
7
11,09
8
10,87
9
12,15
10
10,94
6
4
0
Доход (x),тыс. д.е.
Попытка провести прямую

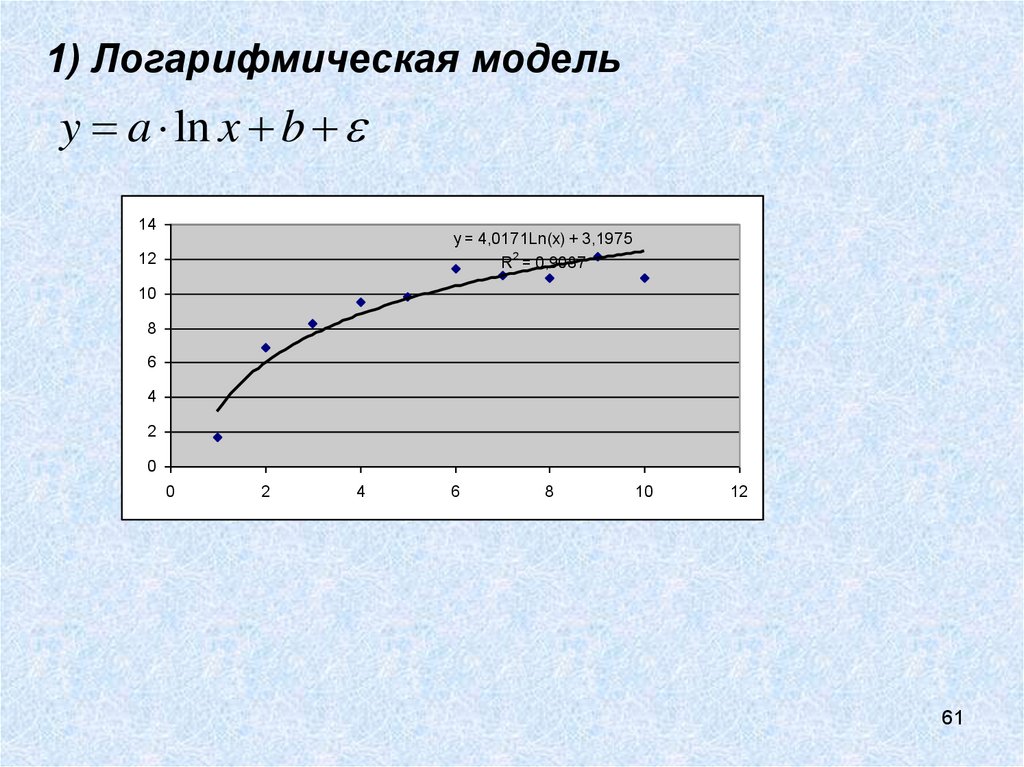
59. 1) Логарифмическая модель

y a ln x b
Для оценки такой зависимости создаем столбец с ln(x)
59

60. 1) Логарифмическая модель

y a ln x b
Используя сервис Анализ данных построим модель линейной регрессии,
используя в качестве зависимой переменной y, а в качестве независимой ln(x).
Y=4.017ln(x)+3.197
60

61. 1) Логарифмическая модель

y a ln x b
14
y = 4,0171Ln(x) + 3,1975
12
2
R = 0,9087
10
8
6
4
2
0
0
2
4
6
8
10
12
61

62. 1) Логарифмическая модель

y a ln x b
Интерпретация коэффициента а: при увеличении х на 1% y увеличится на
а/100 единиц.
Y=4.017ln(x)+3.197
При увеличении дохода на 1% спрос на товар увеличится на
0,0417 единиц.
62

63. 1) Логарифмическая модель

Также как в линейной модели рассчитывается средняя относительная ошибка
аппроксимации
Y=4.017ln(x)+3.197
63

64. Степенная модель

y bx
a
Интерпретация коэффициента a – эластичность
зависимой переменной по объясняющей переменной
a показывает, на сколько процентов возрастает y при
возрастании x на 1%.
64

65. Степенная модель

y bx
a
Сводится к линейной модели логарифмированием
ln y ln b a ln x
65

66. Степенная модель

Создаем столбцы с логарифмами
66

67.

Используя сервис Анализ данных построим модель линейной регрессии,
используя в качестве зависимой переменной ln(y), а в качестве независимой ln(x).
ln(Y)=0.701ln(x)+1.063
67

68.

Используя сервис Анализ данных построим модель линейной регрессии,
используя в качестве зависимой переменной ln(y), а в качестве независимой ln(x).
ln(Y)=0.701ln(x)+1.063
ln y a ln x ln b
ln b 1.063 b exp(1.063) 2.9
68

69.

Используя сервис Анализ данных построим модель линейной регрессии,
используя в качестве зависимой переменной ln(y), а в качестве независимой ln(x).
ln(Y)=0.701ln(x)+1.063
y bx
a
b exp(1.063) 2.9
y 2.9 x
0.701
69

70.

16
y = 2,897x0,7014
14
R = 0,7779
2
12
10
8
6
4
2
0
0
2
y 2.9 x
4
6
8
10
12
0.701
70

71.

Также как в линейной модели рассчитывается средняя относительная ошибка
аппроксимации
y 2.9 x
0.701
71