Эконометрика. Основные типы моделей и данных

1. Эконометрика

Понятие эконометрики.
Основные типы моделей и данных

2. Понятие эконометрики

Эконометрика как наука сформировалась на
основе таких математических дисциплин,
как теория вероятностей и статистика, и
экономической теории.

3. В рамках эконометрики

Экономические связи и зависимости приобретают
строгую математическую форму.
Эконометрические модели предназначены для
качественного анализа экономических ситуаций,
выявления силы влияния отдельных факторов
модели на результирующую характеристику.
При помощи эконометрических методов можно
выявлять новые, ранее не известные связи,
уточнять или отвергать гипотезы о
существовании определенных связей между
экономическими показателями,
предполагаемыми экономической теорией.

4. Эконометрика

– это наука, которая формулирует
экономические модели,
основываясь на экономической теории и
экспериментальных данных,
оценивает параметры этих моделей,
делает прогнозы с некоторой степенью
точности,
которую также можно оценить в рамках
данной науки,
и дает рекомендации по экономической
политике.
Эконометрика как наука связанна с
эмпирическим выводом экономических
законов.

5. Эконометрика

основывается на базовых статистических
разработках и методиках.
Следовательно, математические предпосылки
эконометрических моделей те же, что и в
статистике.
Для обеспечения наивысшей точности
эконометрических прогнозов, эти модели
требуют большого объема статистической
информации.
Кроме того, качество этих моделей зависит от
правильного подхода к формированию модели в
неразрывной связи с ее экономической
интерпретацией.

6. При формировании эконометрических моделей

Требуется четко выделить те факторы, которые
будут в нее включены;
Следует избегать включения в модель
несущественных для данной эконометрической
зависимости факторов, но и опасаться
недооценки влияния некоторых частных
показателей;
Выбор вида связи также оказывает очень
существенное воздействие на эконометрическую
модель, неправильная интерпретация связи
может привести к существенным ошибкам при
прогнозировании.

7. Рассмотрим процесс потребления

Пусть C – потребление некоторого пищевого продукта на
душу населения в некотором году,
Y – реальный доход на душу населения в этом году, а P –
индекс цен на этот продукт, скорректированный
(дефлированный) на общий индекс стоимости жизни.
0, 1, 2 – константы.
Поведение потребителя по отношению к покупке данного
пищевого продукта можно продемонстрировать при
помощи следующей функции:
C= 0+ 1Y+ 2P+
или lnC= 0+ 1lnY+ 2lnP+ ,
С(t)
С(t)

8. Классы эконометрических моделей

Модели временных рядов, которые, в свою очередь
бывают:
◦ Моделями тренда y(t)=T(t)+ t, где T(t) - временной ряд,
t – случайная составляющая.
◦ Моделями сезонности y(t)=S(t)+ t, где S(t) – сезонная
(периодическая) компонента, t – случайная
составляющая.
◦ Моделями тренда и сезонности y(t)=T(t)+S(t)+ t
(аддитивная) или y(t)=T(t)∙S(t)+ t (мультипликативная)
форма модели.
◦ Модели адаптивного прогноза, авторегрессии и
скользящего среднего, общей чертой которых является
то, что они объясняют поведение временного ряда,
исходя из его предыдущих значений.

9. Классы эконометрических моделей

Модели регрессии предполагают задание набора
факторов модели, оказывающих влияние на результат.
Поиск неизвестных параметров этих моделей
осуществляется на базе аппарата регрессионного анализа
математической статистики.
В общем виде, регрессионная модель может быть задана в
следующей форме:
f(x, )=f(x1,…,xk, 1,…, p)+ ,
где x1,…,xk – факторы модели, , 1,…, p – неизвестные
параметры, – случайная составляющая.

10. Классы эконометрических моделей

Системы одновременных уравнений заданы системой
регрессионных уравнений в едином временном интервале
и тождеств.
Примером может служить модель спроса и предложения на
товар широкого потребления:
Q1tD= 1+ 2Pt+ 3Yt+ut (спрос),
Q2tS= 1+ 2Pt+ 3Pt–1+ t (предложение),
Q1tD=Q2tS (тождество, характеризующее равновесие между
спросом и предложением),
где Pt – цена товара в момент времени t, Pt–1 –цена в
предшествующий момент времени, Yt – совокупный доход
населения, ut и t – случайные составляющие функции
предложения и функции спроса.

11. Типы данных в эконометрике

Пространственные данные (объемы
производства, количество работников,
доход в регионе и т. п.);
Временные данные (спрос, инвестиции и
т. п. в привязке ко времени).

12. Обозначения в эконометрике

Модель связи выражается непосредственно функцией,
зависящей от заданных факторов модели и неизвестных
параметров регрессии без учета случайной погрешности. В
случае парной линейной регрессии модель связи можно
записать в следующей форме:
y= + x.
Модель экспериментальных данных или модель
наблюдений позволяет найти значение результирующей
переменной в заданной точке. В случае парной линейной
регрессии модель данных можно записать в следующей
форме
yi= + xi+ i.

13. Эконометрика

Парная линейная функция регрессии.

14. Парная линейная регрессия

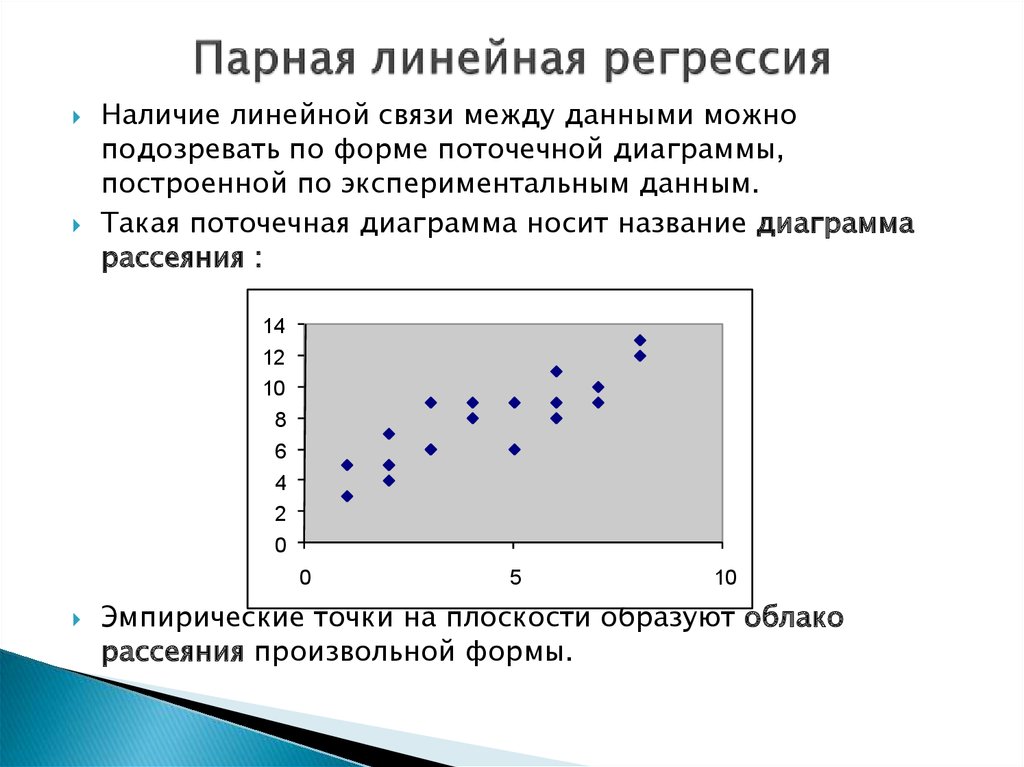
Наличие линейной связи между данными можно
подозревать по форме поточечной диаграммы,
построенной по экспериментальным данным.
Такая поточечная диаграмма носит название диаграмма
рассеяния :
14
12
10
8
6
4
2
0
0
5
10
Эмпирические точки на плоскости образуют облако
рассеяния произвольной формы.

15. Вид парной линейной зависимости

Если облако рассеяния имеет вытянутую в некотором
направлении форму, то это позволяет предполагать
наличие линейной зависимости между фактор-признаком
и результатом.
В случае парной зависимости вытянутая форма облака
рассеяния позволяет предполагать наличие линейной связи
y= + x.
Соотношение между результирующим фактором и факторпризнаком приобретает следующий вид yi= + xi+ i.
При этом i представляет собой отклонение реально
наблюдаемых результатов от значений результирующего
признака, предсказываемого гипотетической линейной
моделью связи y= + x. При этом отклонения i=yi–( + xi).

16. Экономический смысл парной линейной модели

На основе данных о размерах располагаемого дохода xi и
расходов на личное потребление Ci для семейных
хозяйств можно построить парную линейную модель связи
между располагаемым доходом и расходами на личное
потребление:
С= + x,
где – некоторая постоянная величина (0< <1),
характеризующая в данном круге семейных хозяйств их
склонность к потреблению, связанную с традициями и
привычками,
а – коэффициент автономного потребления.

17. Степень выраженности линейной связи показывает

Выборочный коэффициент корреляции:
n
( x x)( y
Cov( x, y)
rxy
Var ( x) Var ( y)
i 1
i
n
( xi x)
2
i 1
i
y)
n
2
(
y
y
)
i
i 1
Величина стоящая в числителе, определяется соотношением:
1 n
Cov ( x , y )
( x i x )( y i y )
n 1 i 1
называется выборочной ковариацией переменных и , при
этом,
n
n
Cov( x, x) Var ( x)
1
1
2
2
(
x
x
)
,
Cov
(
y
,
y
)
Var
(
y
)
(
y
y
)
.
i
i
n 1 i 1
n 1 i 1
n
n 1
Var ( x)
n
2
x
( x x)
i 1
i
n
2
Var ( y )
n 1
n
2y

18. Выраженность линейной связи

Если тенденция линейной связи выражена на диаграмме
рассеяния довольно ясно, то значени rxy по абсолютной
величине близки к единице (т. е. значения близки к +1 или
к –1).
Если
же
наличие
линейной
тенденции
связи
обнаруживается на диаграмме рассеяния с трудом, то
тогда значения rxy близки к нулю.
Значения rxy не зависят от выбора шкал измерения
переменных x и y (если, конечно, эти шкалы линейны).
Близость коэффициента корреляции к +1 означает
наличие прямой линейной связи, а к –1 – обратной.

19. Метод наименьших квадратов

Определение неизвестных параметров функции регрессии
в эконометрике осуществляется на основе стандартного
метода наименьших квадратов (МНК), метода, основанного
на принципе наименьших квадратов.
Принцип наименьших квадратов утверждает, что выбор
параметров функции регрессии является оптимальным в
случае, когда сумма квадратов отклонений эмпирических
значений результирующей переменной от теоретических
значений этой переменной, рассчитанной по функции
регрессии, является минимальной. Математически принцип
наименьших квадратов можно записать следующим
образом:
2
Q( , ) yi yi ( , ) min
i 1
где: yi – расчетное значение тренда, yi – фактическое
значение тренда из ретроспективного ряда, n –число
n
наблюдений.

20. МНК применяется в следующих предпосылках

1.
2.
3.
4.
5.
6.
Случайные ошибки имеют нулевую среднюю (отсутствуют
систематические ошибки), конечные дисперсию и
ковариацию;
Каждое измерение случайной погрешности характеризуется
нулевым средним, не зависящим от значений наблюдаемых
переменных;
Дисперсии каждой случайной ошибки одинаковы, а их
величины независимы от значений наблюдаемых
переменных (гомоскедастичность);
Отсутствует автокорреляция ошибок, то есть значения
ошибок различных наблюдений независимы друг от друга;
Случайные погрешности имеют нормальное распределение;
Значение тренда (внутренней переменной) свободны от
ошибок измерения и имеют конечные средние значения и
дисперсии.

21. Невыполнение этих предпосылок

Может сделать применение
метода некорректным или
привести к чрезмерным ошибкам
прогноза!

22. В соответствии с принципом Лагранжа

n
Q( , ) yi ( x) min
2
i 1
Q
0
Q
0
Эту систему линейных уравнений можно решить
относительно неизвестных и .

23. Возьмем производные

2
2
(
y
(
x
))
Q
i
( yi ( xi )) i
i 1
i 1
n
Q
n
2
2 yi ( xi ) ( 1) 0
(
y
(
x
))
i
i
i 1
i 1
n
n
( yi ( xi )) 2
i 1
n
n
2 yi ( xi ) ( xi ) 0
i 1
Умножим каждое уравнение на ½.

24. Раскроем суммы

n
n
n
yi xi 0
i 1
i 1
i 1
n
n
n
yi xi xi xi 2 0
i 1
i 1
i 1
n xi yi
i 1
i 1
n
n
n
2
xi xi yi xi
i 1
i 1
i 1
n
n
n
1 (1 ... 1) n
n
n
i 1
i 1
1 n
n
n yi n xi
i 1
i 1
n
n
n
2
xi xi yi xi
i 1
i 1
i 1
1 n
n
yi xi
n i 1
n i 1
1 n
n
n
n
n
2
yi xi xi xi yi xi
n i 1
n i 1 i 1
i 1
i 1

25. Получим 

n
n
n 2 1 n 2 n
1
xi xi yi xi yi xi
i 1
i 1
n
i 1
n i 1 i 1
1 n n
yi xi yi xi
n i 1 i 1
i 1
2
n
n
1
2
xi xi
n i 1
i 1
n

26. Решение:

Решение этой системы уравнений дает оценки параметров
линейной функции регрессии по МНК (крышечка означает
МНК-оценку). Оценка равна:
n
1
n
1
y
i n
i 1
n
x
i 1
i
y x.
x , y лежит на прямой y x .
При этом точка
Подстановка выражения для во второе уравнение системы
дает:
2
n
n
2
1
1
y
x
i
i
n
n xi xi yi xi ,
i 1
i 1 i 1
i 1
i 1
n
откуда:
n
n
n n
yi xi yi xi
i 1 i 1
i 1
2
n
n
2
1
x
x
i
n i
i 1
i 1
n
1
n
n
y x nyx
i 1
n
i i
2
2
x
n
x
i
i 1

27. Для доказательства проведем преобразование:

Рассмотрим:
n
2
x
x
i
i 1
n
2
n
2
1
n
2
2
2
xi 2 x xi nx xi 2 xi n x
n n i 1 nn
i 1
i 1
n
i 1
2
2
2
2
n
x
x
1
x
(
1
...
1
)
n
x
2
2
2
2
n
n
n
xi2 2n x n x xi nx ,
i 1
i 1
i 1
i 1
n n
n n
yi y xi x yi xi y xi n x yi n nyx
i 1
i 1
i 1
i 1
n
n
n
n
i 1
i 1
yi xi nyx nyx nyx yi xi nyx .
Последние соотношения позволяют получить более
употребительную форму записи выражения для (в отклонениях
от средних значений):
n
y
i 1
i
n
y xi x
2
x
x
i
i 1
,

28. Решение системы уравнений парной линейной регрессии будет:

y x
n
y
i 1
i
y xi x
n
x
i 1
i
x
,
2
Такое решение может существовать только, если:
n
2
x
x
0,
i
i 1
что равносильно отличию от нуля определителя системы.

29. Действительно этот определитель равен:

n
n xi2 xi n xi2 nx 2
i 1
i 1
i 1
n
n
2
n
n xi x .
2
i 1
Последнее условие называется условием
идентифицируемости модели наблюдений
yi xi i , i 1, , n , и означает попросту, что не
все значения x1 , , x n совпадают между собой. При
нарушении этого условия все точки xi , yi , i 1, , n , лежат
на одной вертикальной прямой x x .
Вспоминая определения ковариации и вариации, видим, что:
Cov( x, y )
.
Var( x )
Отсюда видно, что значения близки к нулю, если
ковариация между наблюдаемыми значениями переменных
x и y близка к нулю, кроме того, знак совпадает со
знаком ковариации Cov x, y , поскольку
Var x 0 .

30. Эконометрика

Коэффициент детерминации.

31. Чтобы ввести коэффициент детерминации

Введем для любой точки xi , yi на диаграмме рассеяния
разложение:
yi y yi y i y i y ,
где y i xi . Возведя обе части последнего представления
в квадрат и просуммировав левые и правые части
полученных для каждого i равенств, получаем:
2
2
n
n
yi y yi y yi yi 2 yi yi yi y .
i 1
i 1
i 1
i 1
n
2
n
Входящая в правую часть сумма называется остаточной
суммой квадратов:
2
n
2
y i y i ei
i 1
i 1
n

32. Докажем, что третья сумма равно нулю

Раскроем третье слагаемое:
n
n
n
n
n
yi y i xi y ei yi y i y i y ei
y
y
y
y
=
i
i
i 1
i 1
i =1
i 1
i 1
n
n
n
ei ( yi yi ) xi y ei 0
i 1
i 1
yi y i ei ,
i 1
n
e
i 1
i
0
Тем самым, останется:
2
y
y
y
y
i
i
n
n
i 1
i 1
2
2
yi y i ,
i 1
n
Слева – полная сумма квадратов, справа – сумма квадратов,
объясненная моделью регрессии и остаточная сумма
квадратов.

33. Исходя из теории

Тенденция линейной связи между x и y выражена в
n
2
максимальной степени, если
e
i 0.
i 1
Тенденция линейной связи между переменными x и y не
обнаруживается вовсе, если
n
n
e yi y .
i 1
2
i
i 1
Таким образом, в качестве «меры выраженности» линейной
связи между переменными можно использовать величину:
2
y
y
i
i
,
R 2 1 i 1n
2
yi y
n
i 1
называемую коэффициентом детерминации. Этот
коэффициент изменяется в пределах
0 R2 1 .
2

34. Исходя из разложения полной суммы квадратов,

Коэффициент детерминации можно представить в форме:
2
yi y i
=
R 2 1 i 1n
2
yi y
n
i 1
2
yi y yi y i
=
i 1
i 1
n
2
yi y
n
n
2
i 1
2
yi y
,
i 1
n
2
yi y
n
i 1
поэтому вторая форма коэффициента детерминации будет:
2
yi y
,
R 2 i n1
2
yi y
n
i 1
то есть отношение суммы квадратов, объясненной моделью
регрессии к полной сумме квадратов.
Таким образом, значение R2 тем выше, чем больше доля
объясненной моделью суммы квадратов по отношению к полной
сумме квадратов. Вследствие этого, привлечение информации о
значениях переменной не дает ничего нового для объяснения
изменений значений y от наблюдения к наблюдению.

35. Коэффициент детерминации

Оценивается следующими способами:
2
y
y
i
i
,
R 2 1 i 1n
2
y
y
i
n
i 1
2
y
y
i
,
R 2 i n1
2
y
y
i
n
i 1
rxy2 R 2 .

36. Степень изменчивости результирующей переменной

характеризуется значением выборочной дисперсии:
1 n
2
Var ( y )
y
y
i
n 1 i 1
При этом вариацию можно разложить на объясненную
регрессией и остаточную вариацию:
2
yi y
yi y
i
1
i 1
= Var ( y ) ,
n 1
n 1
где y – переменная,
принимающая в i–м наблюдении
значение y i . (Здесь мы использовали тот факт, что
n
2
n
e
0
,
y
y
так что i
i
i 0,
i 1
i 1
n
n
и
y y
n
n
y y
i 1
i
i 1
i

37. Тем самым,

2
n
n
2
2
y
y
e
e
e
i
i
i
i
i 1
i 1
i 1
= Var(e) ,
n 1
n 1
n 1
где – переменная, принимающая в i–м наблюдении
значение ei .
В итоге, мы получаем разложение:
n
e
Var( y ) Var( y ) Var(e)
показывающее, что изменчивость переменной (степень
которой характеризуется значением Var ( y) ) частично
объясняется изменчивостью переменной
y
(степень которой характеризуется значением Var( y ) )

38. Не объясненная

y часть изменчивости переменной y соответствует
изменчивости переменной e (степень которой выражается
Var ( e) ).
Таким образом, вспомогательная переменная y берет на
себя объяснение некоторой части изменчивости значений
переменной y, и эта объясненная часть будет тем больше,
чем выше значение коэффициента детерминации R 2 ,
который мы теперь можем записать также в виде:
Var( y )
Var(e)
1
Var( y )
Var ( y )
Поскольку переменная yполучается линейным
преобразованием
переменной х, то изменчивость y однозначно связана с
изменчивостью х, так что, в конечном счете, построенная модель
объясняет часть изменчивости переменной y изменчивостью
переменной x. Поэтому, y называют объясняемой переменной, а
x – объясняющей переменной.
R2

39. Эконометрика

СВОЙСТВА ВЫБОРОЧНЫХ ДИСПЕРСИИ, КОВАРИАЦИИ,
КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ И ПАРАМЕТРА
РЕГРЕССИИ.

40. Рассмотрим свойства выборочной функции ковариации

Пусть а – некоторая постоянная, а xi , yi , z i – переменные, в
i–м наблюдении, i 1, , n (n – количество наблюдений).
Тогда а можно рассматривать как переменную, значения
которой в i-м наблюдении равно а. Можно выделить ряд
свойств ковариации. Итак,
1.
Cov(x,a)
n
1
n 1
(x
i 1
i
x )(ai a )
так что Cov( x, a) 0
2. Cov( x, y) Cov( y, x)
3. Cov ( ax , y )
так что
n
1
n 1
( ax
i
n
1
n 1
x x a a ,
i 1
i
.
Cov( x, x) Var ( x) .
ax )( yi y ) a
i 1
Cov( ax, y) a Cov( x, y) .
n
1
n 1
x
i 1
i
x yi y ,

41. Свойства ковариации

4.
Cov( x, y z )
x x ( y
n
1
n 1
i 1
i
i
поэтому:
n
1
n 1
( x x )( y
i
i 1
i
zi ( y z ))
y ) ( zi z )
n
1
n 1
x x y
i 1
i
n
i
y + n1-1 xi x zi z ,
i 1
Cov( x, y z) Cov( x, y) Cov( x, z) .

42. Свойства выборочной вариации

1.
2.
Постоянная не обладает изменчивостью: Var ( a) 0
При изменений единицы измерения переменной в а раз,
во столько же раз изменяется и величина стандартного
отклонения этой переменной:
Var (ax) a 2Var ( x),
3.
4.
т.е.
Сдвиг начала отсчета не влияет на изменчивость
переменной: Var( x a ) Var( x )
Дисперсия суммы двух переменных отличается от суммы
дисперсий этих переменных на величину, равную
удвоенному значению ковариации между этими
переменными:
Var ( x y ) Cov( x y, x y )
Cov( x, x) Cov( x, y ) Cov( y, x) Cov( y, y ) ,
Var ( x y) Var ( x) Var ( y) 2Cov( x, y)

43. Свойства выборочного коэффициента корреляции

При изменении начала отсчета и единицы измерения
коэффициента корреляции rxy
он остается инвариантен относительно изменения системы
координат (выбора единиц изменения и начала отсчета
переменных х и y).
Если изменяется начало переменной х и вместо переменных
x1 , , x n будут значения:
x~i a bxi , i 1, , n,
Тогда:
(b 0) , т.е. ~
x a bx
Cov( ~
x , y)
Cov(a bx, y )
r~x y
~
Var ( x ) Var ( y )
Var ( a bx) Var ( y )
Cov(bx, y )
bCov( x, y )
rxy .
2
Var (bx) Var ( y )
b Var ( x) Var ( y )

44. Свойства параметра регрессии

Оценка
x параметра регрессии в модели наблюдений
yi xi i , i 1, , n.
инвариантна относительно изменения системы координат не
будет .
~
Если перейти к новой системе координат , так что x a bx
,
Cov( ~
x , y ) Cov(a bx, y ) bCov( x, y ) 1
2
x .
~
x
то
~
Var ( x )
Var (a bx)
b Var ( x)
b
Таким образом, изменяя единицу измерения переменной x (или
переменной
y), мы можем получать существенно различные
значения от сколь угодно малых, до сколь угодно больших.
(Желательно выбирать единицы измерения таким образом, чтобы
сравниваемые переменные
имели одинаковый порядок.).
Близость значений к нулю всегда должна интерпретироваться
с оглядкой на используемые единицы измерения переменных x и
y.

45. Коэффициент корреляции наблюдаемого значения результата и оценки по МНК-методу

r
Рассмотрим теперь коэффициент корреляции y y
y
y
между переменными и , где y x , а и оценки
параметров регрессии и .
Замечая, что y y e (т.к. ei y i y i по определению),
находим:
r
yy
Cov( y , y )
Var ( y ) Var ( yˆ )
Cov( y e, y )
Var ( y ) Var ( y )
Cov( y , y ) Cov(e, y )
Var ( y ) Var ( y )
.

46. Но ранее было доказано, что

Соотношение y i y i y i y 0 , а с учетом того, что
i 1
n
yi y i 0
i 1
n
n
1
приходим к утверждению:
yi y i y i 0 Cov(e, y ) Cov( y y, y ) 0
n 1 i 1
Следовательно: r
yy
так что r 2 Var( y ) R 2 .
yy
Var ( y )
Var ( y ) Var ( y )
Var ( y )
,
Var ( y )
Var( y )
Следовательно, коэффициент детерминации равен квадрату коэффициента
корреляции между переменными y и y . При достаточно сильно
выраженной линейной связи между переменными x и y , что соответствует
значению R2, близкому к 1, r тоже стремится к 1. r называют
yy
yy
множественным коэффициентом корреляции и обозначают символом R.
y
Отметим также, что переменная измеряется в тех же единицах, что и
переменная y, и при изменении масштаба измерения переменной y значение
r не изменяется. Отсюда вытекает, что коэффициент детерминации
yy
R2 инвариантен относительно изменения масштаба и начала отсчета
переменных x и y.

47. В результате получим

Множественный коэффициент корреляции в виде:
r
Cov( y , y )
yy
Cov( y , x )
Var ( y ) 2Var ( x )
Var ( y ) Var ( x )
Var ( y ) Var ( y )
Cov( y , x )
sign ( ) Cov( y , x )
Var ( y ) Var ( x )
.
(здесь sign(z)=–1 для z<0, sign(z)=0 для z=0, sign(z)=1 для
z>0)
Cov( x, y )
, то sign( ) sign (Cov( x, y )) , и
Поскольку же:
Var ( x )
r
yy
2
sign (Cov( x, y )) rxy ,
r R2 ,
2
xy
Т.е.
yy
и мы можем установить значение R2 еще до построения
модели линейной связи.
r

48. В заключении

Коэффициент детерминации необходимо оценивать тремя
различными способами:
2
y
y
i
i
,
R 2 1 i 1n
2
y
y
i
n
i 1
2
y
y
i
,
R 2 i n1
2
y
y
i
n
i 1
r 2 rxy2 R 2 .
yy