Похожие презентации:
Двулучепреломление
1. Двулучепреломление.
Оптическая ось.
Двулучепреломление.
Двулучепреломление в одноосном
кристалле.
Линейно поляризованная волна в
одноосном кристалле.
Эллиптичность волны
Случай изотропной среды
2. Магнитооптические материалы.
• Магнитооптическая добротность• Пленки ферритов-гранатов.
Выращивание
Магнитооптические свойства
Эффект Фарадея в двухподрешеточном
ферримагнетике
• Ортоферриты
• Борат железа
3. Магнитооптическая добротность
I – интенсивность света, прошедшегочерез пластинку толщиной z,
Io – интенсивность падающего света,
α – коэффициент поглощения,
φ – угол «падения».
I I o e z cos 2
I I o e z cos 2 I o e z cos 2 2 I o e z sin 2 2 F z
2
θF – удельное фарадеевское вращения.
4. Выберем оптимальную толщину образца, чтобы интенсивность свет, проходящего через него, была максимальной.
II o e z sin 2 2 F z 2 sin 2 F z cos 2 F z 2 F e z
z
I
0
z
sin 2 F z 4 F cos 2 F z 0
1
4 F
z
arctg
2 F
2 F
- оптимальная толщина образца
- магнитооптическая добротность
град см
град
см
5. Вычислим интенсивность света, прошедшего через образец при оптимальной толщине образца.
I I oeI oe
I oe
4 F
arctg
2 F
1
4 F
arctg
2 F
4 F
arctg
2 F
1
4 F
sin 2 F
arctg
2 F
2
4 F
sin arctg
4 F
2
2 F
f
2
4 F
1
Эта интенсивность – функция добротности
6. Прозрачные ферромагнетики: ферриты-гранаты, ортоферриты и борат железа.
Нельсон и Дирборн [Neilson J.W., Dearborn E.F. PhysicsChem. Solids, 5, 202 (1958)] вырастили монокристаллы
непроводящего железоиттриевого граната Y3Fe5O12.
Примерно в то же время были выращены кристаллы
ортоферрита иттрия YFeO3.
Борат железа FeBO3 известен с 1963 г. Свойства
исследованы в 1975.
Эти материалы прозрачные в видимой и ИК области
спектра и обладают большим удельным фарадеевским
вращением.
7. Ферриты-гранаты Технология изготовления ЦМД чипа
Выращивание кристаллов немагнитных гранатовдля подложек
Изготовление самих подложек из массивных
кристаллов
Выращивание магнитных цмд пленок на
подложках
Обработка цмд пленок (например, ионная
имплантация для подавления жестких цмд)
Создание управляющих структур на цмд пленке
Разрезание полученных пластин на одиночные
приборные чипы.
8. Выращивание подложек
(немагнитная и монокристаллическая, твердая, плоская, гладкая,бездефектная, обладать малой электропроводностью и большой
теплоемкостью, постоянная решетки подложки должна быть близка
к постоянной решетки пленки)
Выращивание монокристаллов гранатов по методу Чохральского
Скорость роста 0,8 – 1,5 см/ч,
температура раствора-расплава 1700 С,
скорость вращения 20-25 об/мин.
9.
Ян Чохра́льский(1885 — 1953) —
польский химик,
изобретатель широко
известного в настоящее
время метода
выращивания
монокристаллов из
расплава путём
вытягивания их вверх от
свободной поверхности,
названного впоследствии
его именем.
10. Подготовка подложки.
Для получения из монокристаллической булизаконченной подложки необходимо
выполнить операции:
С помощью оптического контроля определить
ориентацию
Разрезать булю на пластинки
Отполировать их поверхность: сначала
механически, а потом химически (горячей
фосфористой кислотой). При полировке
снимается около 120 мкм.
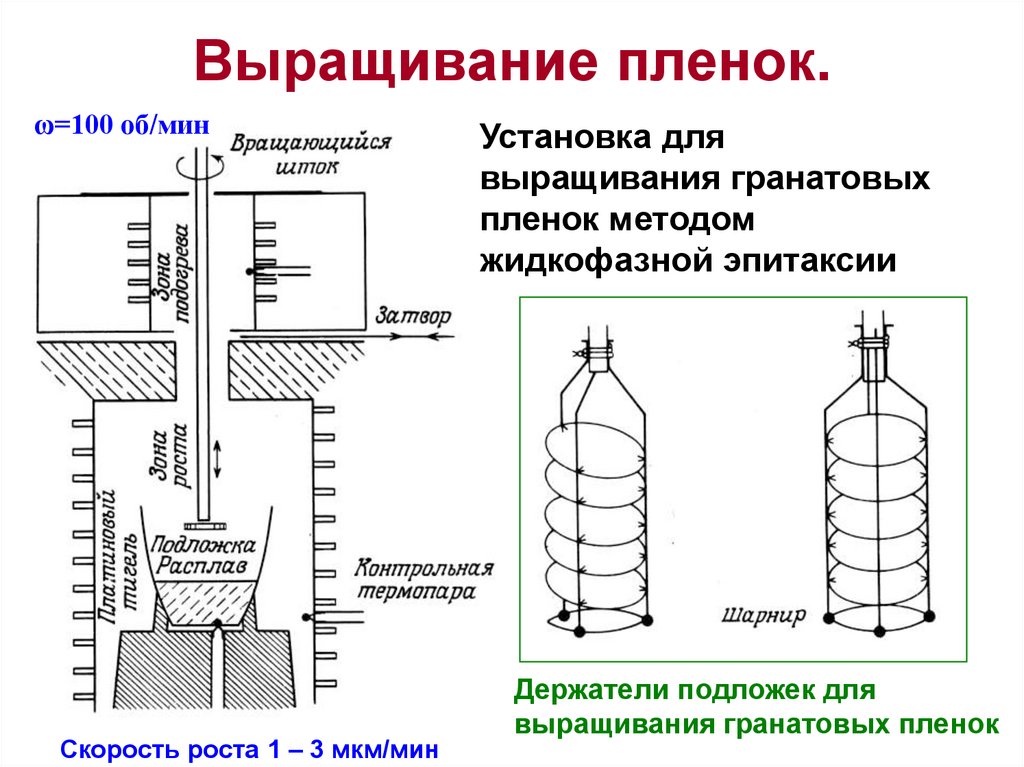
11. Выращивание пленок.
ω=100 об/минСкорость роста 1 – 3 мкм/мин
Установка для
выращивания гранатовых
пленок методом
жидкофазной эпитаксии
Держатели подложек для
выращивания гранатовых пленок
12. Установка по выращиванию монокристаллов по методу Чохральского (НПО «Карат», Львов, Украина)
Кристаллическаябуля
Cd3Ga5O12:Nd
направление
выращивания
[111]
13.
Станок прецизионной резкимонокристаллических
материалов
Технологическая линия
шлифовальнополировальных станков
Лазерный интерферометр
для контроля качества
обработки рабочих
поверхностей
монокристаллических
оптических элементов
14. Установка для выращивания монокристаллических слоев методом жидкофазной эпитаксии
Эпитаксиальныепленки на
подложке из
гадилинийгаллиевого
граната
15. Ферриты-гранаты
{M33+}(Fe33+)[Fe23+]O12; {} – додекаэдрическая, () –тетраэдрическая и [] – октаэдрическая подрешетки.
Ферриты-гранаты M3Fe5O12, M – трехвалентный ион Y, Cd, Dy,
Ho, Er, Tm, Lu, Yb, Sm, Er, Tb. Кристаллическая структура
изоморфна структуре граната Сa3Al2(SiO4)3. В элементарной
ячейке граната содержится 8 формульных единиц.
16. Ферриты-гранаты.
• Сильновзаимодействующиеподрешетки железа можно
считать единой подрешеткой.
Следовательно в первом
приближении магнитную
структуру граната можно считать
двухподрешеточной.
• Точка Нееля редкоземельных
ферритов-гранатов практически
не зависит от входящих в них
редкоземельных ионов
(TN=563±15o К).
Размер доменов от 0,1 до 103 мкм;
Намагниченность насыщения до 2∙103 Гс;
Константа одноосной анизотропии от 10-3 до 105 эрг/см3;
Параметр затухания Гильберта от 10-4 до 1.
17.
Температурная зависимостьпарциальных и результирующей
намагниченностей в случае, когда
существует температура компенсации.
18.
Температурная зависимость намагниченностейнекоторых редкоземельных ферритов-гранатов.
19. Основные механизмы вращения плоскости поляризации света в ферритах-гранатах. (R3Fe5O12)
• Гиромагнитный, связан с ферромагнитным иобменным резонансами, собственные частоты
которых лежат в далекой ИК области;
• Гироэлектрический обменный, связан с обменным
расщеплением энергетических уровней
редкоземельных ионов;
• Гироэлектрический спин-орбитальный, связан со
спин-орбитальным расщеплением энергетических
уровней ионов железа;
• Гироэлектрический, связан с интенсивными
электронными переходами в редкоземельный ионах,
собственные частоты которых расположены в УФ
области спектра.
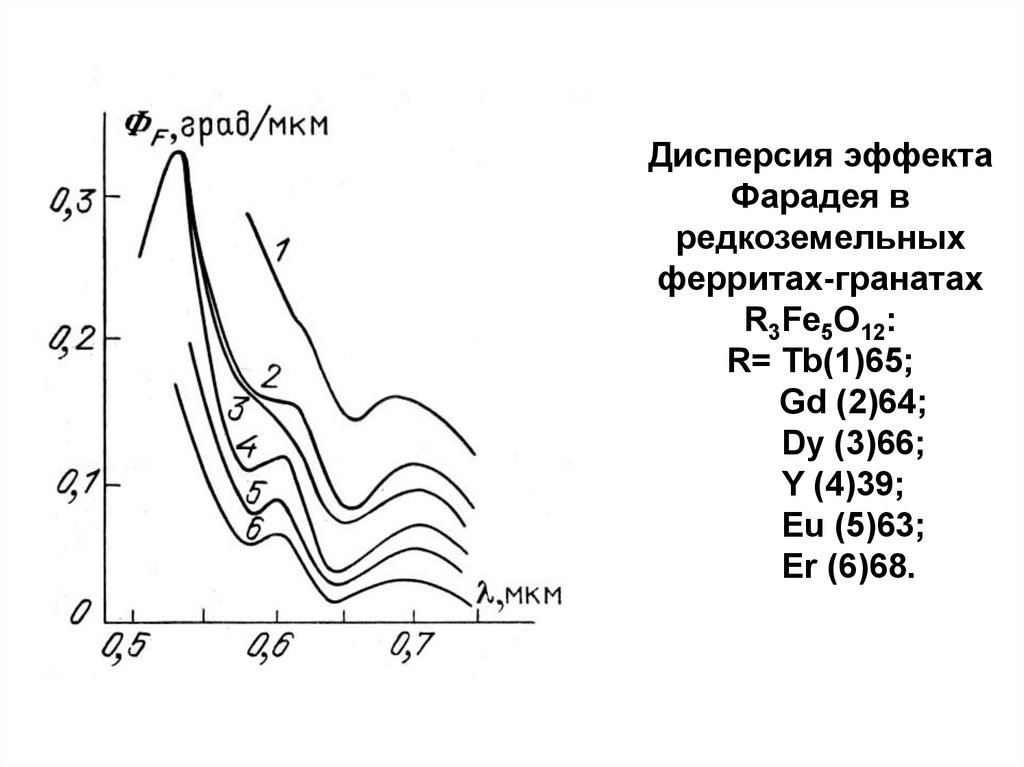
20. Дисперсия эффекта Фарадея в редкоземельных ферритах-гранатах R3Fe5O12: R= Tb(1)65; Gd (2)64; Dy (3)66; Y (4)39; Eu (5)63; Er
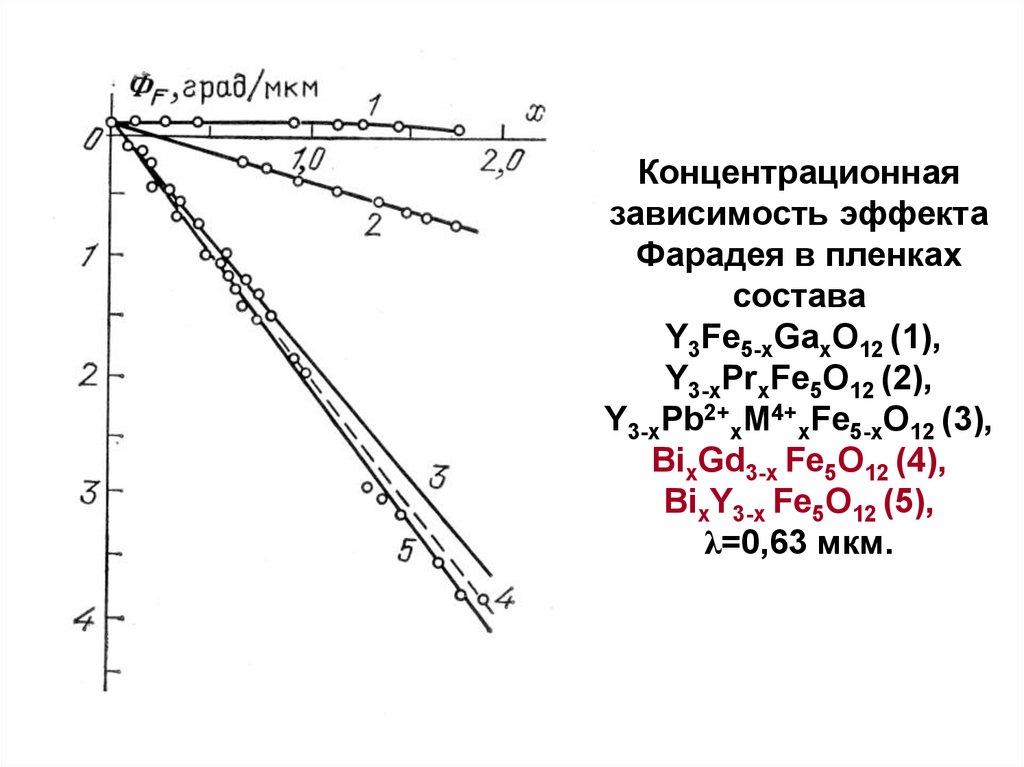
(6)68.21. Концентрационная зависимость эффекта Фарадея в пленках состава Y3Fe5-хGaхO12 (1), Y3-хPrхFe5O12 (2), Y3-хPb2+хM4+xFe5-xO12 (3),
BixGd3-x Fe5O12 (4),BixY3-x Fe5O12 (5),
λ=0,63 мкм.
22. Спектры удельного фарадеевского вращения системы R3-xBixFe5O12 с различным содержанием висмута.
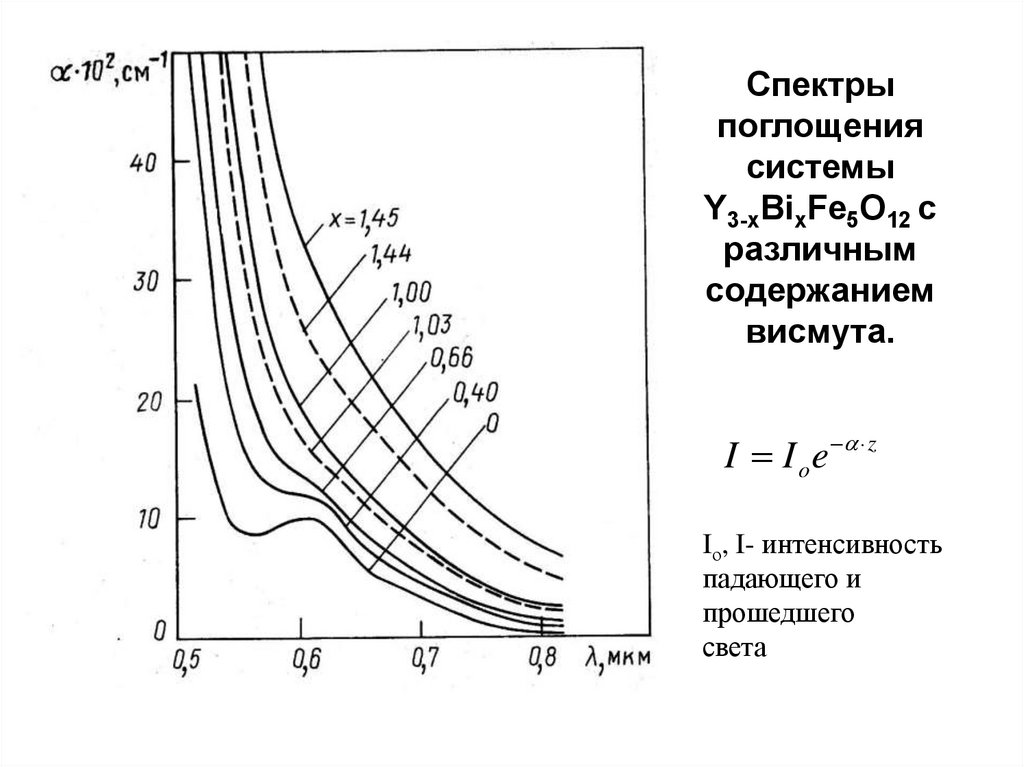
23. Спектры поглощения системы Y3-xBixFe5O12 с различным содержанием висмута.
I I o e zIо, I- интенсивность
падающего и
прошедшего
света
24. Ферриты-гранаты
• В первом приближении магнитнуюструктуру граната можно считать
двухподрешеточной.
• Магнитные свойства изменяются в
широком диапазоне.
• Материалы удобные для
магнитооптических исследований.
25. Эффект Фарадея в двухподрешеточном ферримагнетике
d M1обм
1 ( H H1 ) M 1
dt
d M 2
( H H обм ) M
2
2
2
dt
обм
11 M 1 12 M 2
обм
21 M 1 22 M 2
H1
H2
0
0
В состоянии равновесия М1 и М2
ориентированы антипараллельно,
и вектор намагниченности
M M1 M 2
при насыщении направлен
параллельно магнитному полю Н
обменные константы
26.
С учетом вида тензора νH1
обм
M 2
обм
M1
H2
Уравнения Ландау-Лифшица имеют вид:
Эти уравнения описывают
прецессию векторов М1 и М2,
связанных друг с другом
обменным взаимодействием,
которое характеризуется
константой обменного поля ν.
Найдем собственные
частоты этой системы, т.е.
частоты, с которыми вектора
М1 и М2 могут совершать
когерентное прецессионное
движение вокруг положения
равновесия.
d M1
обм
1 H M 1 1 H1 M 1
dt
d M 2
H обм M
H
M
2
2
2
2
dt
2
d M1
1 H M 1 1 M 2 M 1
dt
d M 2
dt 2 H M 2 2 M 1 M 2
27.
Разложим М1 и М2 на статические и динамические составляющиеМ 1, 2 M 1o, 2 m1, 2
При этом
M
o
1, 2
m1, 2
m1, 2 ei t
и
M 1o, 2
Если ось z параллельна полю H и
, то из-за симметрии
системы относительно этой оси, обе динамические составляющие
должны обладать круговой поляризацией в плоскости ху. Поэтому
для них справедливы соотношения:
m(1, 2) x m(1, 2) ei t
m(1, 2) y im(1, 2) x im(1, 2)ei t
Направления вращения
определяются знаком ω.
векторов
m1
и
m2
одинаковы
Подставляя векторы М1 и М2 в виде сумм динамических и
статических слагаемых, проектируя уравнения на оси
координат, получим уравнения для амплитуд
и
28. Запишем уравнения системы
m1ei ti
d
im1ei t 1 0
dt
M 1o
m1ei t
j
0
im1ei t
k
i
H 1 m2ei t
M 1o
m1ei t
m2ei t
i
d
im2ei t 2 0
dt
M 2o
m2ei t
j
0
im2ei t
k
i
H 2 m1ei t
M 2o
m2ei t
j
im2ei t
im1ei t
j
im1ei t
im2ei t
k
M 2o
M 1o
k
M 1o
M 2o
Уравнение для х компонент первого и второго уравнений:
im He im M
i m1ei t 1 im1He i t 1 im2 M1o ei t im1M 2o ei t
i m2ei t
i t
2
2
2
1
o i t
2
e
im2 M1o ei t
29.
Сгруппируем по m1 и m2:o
o
m1 1 H 1 M 2 1 M 1 m2 0
o
o
M
m
m
H
M
2
2
2
1 0
2 2 1
Где
M1o, 2 M1, 2
M1, 2 M1, 2 и M1>M2
Однородная система уравнений имеет решение, если
ее определитель равен нулю.
1H 1 M 2 2 H 2 M1 1 2 2 M1M 2 0
2 H 1 2 2 M 1 1M 2 1 2 H 2
H 1 2 M 1 M 2 0
30.
1, 21
Н 1 2 2 M 1 1M 2
2
0
H 2 1 2 H 1 2 1M 2 2 M 1 1M 2 2 M 1
2
2
2
2 0,5
Обменные поля составляют порядка 105 – 107 Э и, следовательно,
как правило H << M 1 M 2
Преобразуем
для
выражения
1, 2
Пренебрежем первым слагаемым под корнем и разложим в ря
1, 2
1
H 1 2 1M 2 2 M 1
Н 1 2 2 M 1 1M 2 1 1
2
2
2 M 1 1M 2
Рассмотрим «высокую» и «низкую» частоты
31.
«Высокая» частота0
0
1
H 1 2 1M 2 2 M 1
1 Н 1 2 2 M 1 1M 2 2
2
2
1M 2 2 M 1
Пренебрежем слагаемыми с Н
1
1
2 2 M 1 1M 2 2 M 1 1M 2
2
Эта частота определяется эффективным обменным
полем – частота обменного резонанса.
1 обм
Лежит в далекой ИК области.
32. «Низкая» частота
H 1 2 1M 2 2 M 11
2 Н 1 2 2 M 1 1M 2
2
2
2 M 1 1M 2
H
2
2 1 2 M 1 2 1 2 M 2 2 H 1 2
2
2 M 1 1M 2
M1 M 2
H
эфф H r
M1 M 2
1
эфф
2
M1 M 2
M1 M 2
1
2
M1 M 2
2 M 1 1M 2
Частота ωr не зависит от константы
молекулярного поля и совпадает с
обычной резонансной частотой
ферромагнетика с гиромагнитным
отношением γэфф.
Величина γэфф характеризует гиромагнитные свойства
вещества как единой системы и имеет смысл только в том
случае, когда вектора М1 и М2 параллельны. В случае, когда
γ1=γ2, ωr – это частота ферромагнитного резонанса.
Эта частота находится в СВЧ области.
33. Типы прецессий в ферримагнетике с двумя подрешетками M1>M2.
Типы прецессий в ферримагнетике с двумяподрешетками M1>M2.
Частоты ωr и ωобм
имеют
противоположные
знаки, следовательно,
соответствующие им
прецессии происходят
в противоположных
направлениях.
Т.о. ферримагнетик с двумя подрешетками имеет две различные
собственные частоты. Одна из них совпадает с резонансной
частотой ферромагнетика, а вторая является прямым следствием
наличия подрешеток.
34. Если в уравнение Ландау-Лифшица добавить член, учитывающий высокочастотное поле, и решить его аналогично случаю ферромагнетика,
то можно получить выражения для компонент тензоравосприимчивости.
M o
Удельное фарадеевское вращение
F
в ферромагнетике:
c
Аналогичный расчет для двухподрешеточного ферримагнетика
при ω >> ωr, ωобм
F
1M 1 2 M 2
c
Переписывая
эту формулу в виде
M M1 M 2
эфф
M1 M 2
M1 M 2
1
2
эфф M 1M 2 1 2 2
F
эфф M
c
1 2 M
видно, что θF определяется вкладом как
ферромагнитного (первое слагаемое), так и
обменного резонансов.
35.
Эффект Фарадея в ферритах-гранатах иттрия (Y), эрбия (Er) игольмия (Ho) в инфракрасной области спектра при Т=290оК и
в феррите-гранате иттрия при Т=77оК
Частотно-независимый эффект Фарадея – следствие
магнитной восприимчивости на оптических частотах.
36. Магнитооптические материалы.
• Магнитооптическая добротность• Пленки ферритов-гранатов.
Выращивание
Магнитооптические свойства
Эффект Фарадея в двухподрешеточном
ферримагнетике
• Ортоферриты
• Борат железа
































 Физика
Физика








