Похожие презентации:
Продольные и поперечные магнитооптические эффекты. Распространение электромагнитной волны в среде. Уравнения Максвелла
1. Уравнение Ландау-Лифшица. Тензор магнитной проницаемости и восприимчивости.
Из каких соображений было получено уравнение
Ландау-Лифшица?
Что описывает это уравнение?
Что мы получили с помощью этого уравнения?
Зачем уравнение Ландау-Лифшица вводят
релаксационный член?
Что такое ферромагнитный резонанс?
Какова структура тензора магнитной
восприимчивости?
Как зависят от частоты действительная и мнимая
компоненты тензора магнитной восприимчивости?
Какова величина диагональной компоненты
тензора μ на оптических частотах?
2. Продольные и поперечные магнитооптические эффекты.
• Распространение электромагнитной волныв среде. Уравнения Максвелла
• Показатель преломления при продольном
распространении волны
Гироэлектрическая, гиромагнитная и
бигиротропная среды
Частотно независимый эффект Фарадея
• Показатель преломления при поперечном
распространении волны
3. Тензор магнитной проницаемости
o M o1 4 2
2
o
i M o
4 2 2
o
0
i M o
4 2
2
o
o M o
1 4 2
2
o
0
0
0
1
o M o
4 107 1010 103
7
4 2
10
10 28
o 2
Поправка к 1 в
диагональной компоненте
M o
4 107 1014 103
3
4 2
10
10 28
o 2
Недиагональная
компонента
4. Уравнения Максвелла
1 Drot H
c t
D E
div D 0
1 B
rot E
c t
B H
div B 0
i Q
i Q
0
0
0
0
o
i Q'
i Q'
0
0
0
0
o
5.
Электромагнитная волнаE Eo e
i ( t
x y z
c
n)
H H oe
i ( t
x y z
c
;
α, β и γ – направляющие косинусы
электромагнитной волны.
1
2
2
2
n – комплексный показатель преломления.
n)
6. Вектор
DE Eo e
i Q
D E i Q
0
0
i ( E x E y i Q )
D
i ( E x i Q E y )
t
i E z o
0
Ex
i ( t
x y z
c
E x E y i Q
0 E y E x i Q E y
o Ez
E z o
n)
7. Вектор
Bi Q '
B H i Q '
0
0
i ( H x H y i Q ' )
B
i ( H xi Q ' H y )
t
i H z o
0
Hx
H x H y i Q '
0 H y H xi Q ' H y
o H z
H z o
8.
rot Hi
rot H
x
Hx
j
y
Hy
H z H y
i
z
y
k
z
Hz
H x H z H y H x
j
k
x x
y
z
9. Компоненты
rot HH H oe
i ( t
x y z
c
n)
H z
i n
Hz
y
c
H x
i n
Hx
z
c
H y
H y
H z
i n
Hz
x
c
H x
i n
Hx
y
c
i n
Hy
z
c
i n
Hy
x
c
i n
i n
rot H i
H z
H y
c
c
i n
i n i n
i n
j
H x
H z k
H y
H x
c
c
c
c
10. Имеем уравнения
ii
nH z nH y Ex i QE y
c
c
i
i
nH x nH z i QE x E y
c
c
i
i
nH y nH x o Ez
c
c
11.
rot Ei
rot E
x
Ex
j
y
Ey
k
z
Ez
Ez E y Ex Ez E y Ex
j
i
k
z z
x x
y
y
12. Компоненты
rot EE Eo e
i ( t
x y z
c
n)
Ez
i n
Ez
y
c
Ex
i n
Ex
z
c
E y
E y
E z
i n
Ez
x
c
Ex
i n
Ex
y
c
i n
Ey
z
c
i n
Ey
x
c
i n
i n
rot E i
Ez
E y
c
c
i n
i n i n
i n
j
Ex
Ez k
Ey
Ex
c
c
c
c
13. Имеем уравнения
ii
nEz nE y H x i Q' H y
c
c
i
i
nEx nEz i Q' H x H y
c
c
i
i
nE y nEx o H z
c
c
14. Система уравнений для компонент векторов и
Система уравнений для компонентвекторов E и H
nH z nH y E x i QE y
nH nH i QE E
x
z
x
y
nH y nH x o E z
nE nE H i Q ' H
z
y
x
y
nE x nE z i Q ' H x H y
nE y nE x o H z
15. Расположим компоненты векторов и по порядку
Расположим компоненты векторовE
и H по порядку
E x i QE y nH y nH z 0
i QE E nH nH 0
x
y
x
z
o E z nH x nH y 0
nE nE H i Q ' H 0
y
z
x
y
nE x nE z i Q' H x H y 0
nE x nE y o H z 0
16. Однородная система имеет решение, если ее определитель равен нулю
i Qi Q
0
0
n
n
n
0
0
0
0
n
n
n
0
n
i Q'
0
0
o
n
n
n
n
i Q'
n
0
0
0
o
0
0
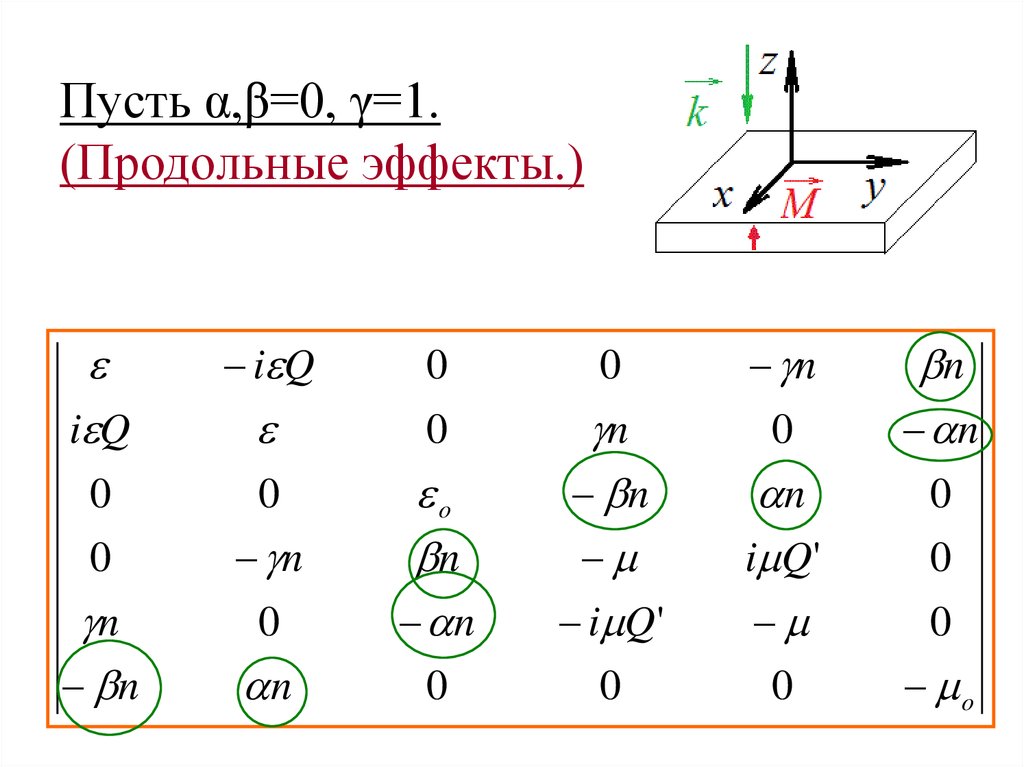
17. Пусть α,β=0, γ=1. (Продольные эффекты.)
i Qi Q
0
0
n
0
0
0
0
n
n
n
0
n
i Q'
0
0
o
n
n
n
n
i Q'
n
0
0
0
o
n
n
0
0
18. Пусть α,β=0, γ=1. (Продольные эффекты.)
i Qi Q
0
0
n
0
0
n
0
0
0
0
o
0
0
0
0
n
0
i Q '
0
n
0
0
i Q'
0
0
0
0
0
0
o
По шестой строке и шестому столбцу
19.
i Qi Q
o
0
0
n
0
n
0
0
0
o
0
0
0
n
0
i Q'
n
0
0
i Q'
По третьей строке и третьему столбцу
20.
o oi Q
i Q
0
n
n
0
0
n
i Q'
n
0
i Q'
По первой строке
21.
n0
i Q
n
0
o o n
i Q' i Q 0
i Q'
0 i Q'
n i Q'
i Q
n 0
n
n o o 2 2Q'2 n 2
0 i Q'
n
i Q i 2 Q i n 2Q' i 2 QQ '2 n QQ' n n n3
o o n 4 n 2 QQ ' QQ ' 2 2 2 2Q'2
2 2Q 2 2 2Q 2Q'2 0
22. Имеем биквадратное уравнение относительно n
n 4 n 2 2 2 QQ' 2 2 1 Q'2 Q 2 Q 2Q'2 0n 4 2n 2 1 QQ' 2 2 1 Q'2 Q 2 Q 2Q'2 0
D 4 1 QQ ' 4 2 2 1 Q'2 Q 2 Q 2Q'2
2
2
2
4 2 2 1 2QQ ' Q 2Q'2 1 Q'2 Q 2 Q 2Q'2
4 Q Q'
2
2
2
0
2 (1 QQ ' ) 2 (Q' Q) 2
n1, 2
(1 QQ ' (Q' Q))
2
2
2
n1, 2 (1 (Q' Q))
2
23. Поворот плоскости поляризации
d dn1 n2 d n
t d
c
c c
V1 V2
d – толщина пластинки, n – показатель преломления
n1, 2 (1 (Q' Q))
2
Учтем, что
Q' Q 1
n1, 2 (1 (Q' Q)) 1 (Q' Q)
0, 5
1 0,5(Q' Q)
24. Поворот плоскости поляризации
d nc
d
c
d
c
d
c
d
c
Q' Q
1 0,5(Q' Q) 1 0,5(Q' Q)
Для бигиротропной среды
Q
Для гироэлектрической среды
Q'
Для гиромагнитной среды
Напомним, что
xy 4
i M o
i M o
4
o 2 2
2 o 2
25. Вращение плоскости поляризации в гиромагнитной среде
dc
Q'
i M o
i M o
xy 4 2
4 2
i Q '
2
2
o
o
Учитывая, что
4 M o
Q'
2 o 2
следовательно
Q'
4 M o
2
d
c
При ω>>ωo
4 M o
d 4 M o 4 d M o
Q'
c
с
Вращение
плоскости
поляризации в
гиромагнитной
среде не зависит
от длины волны
26.
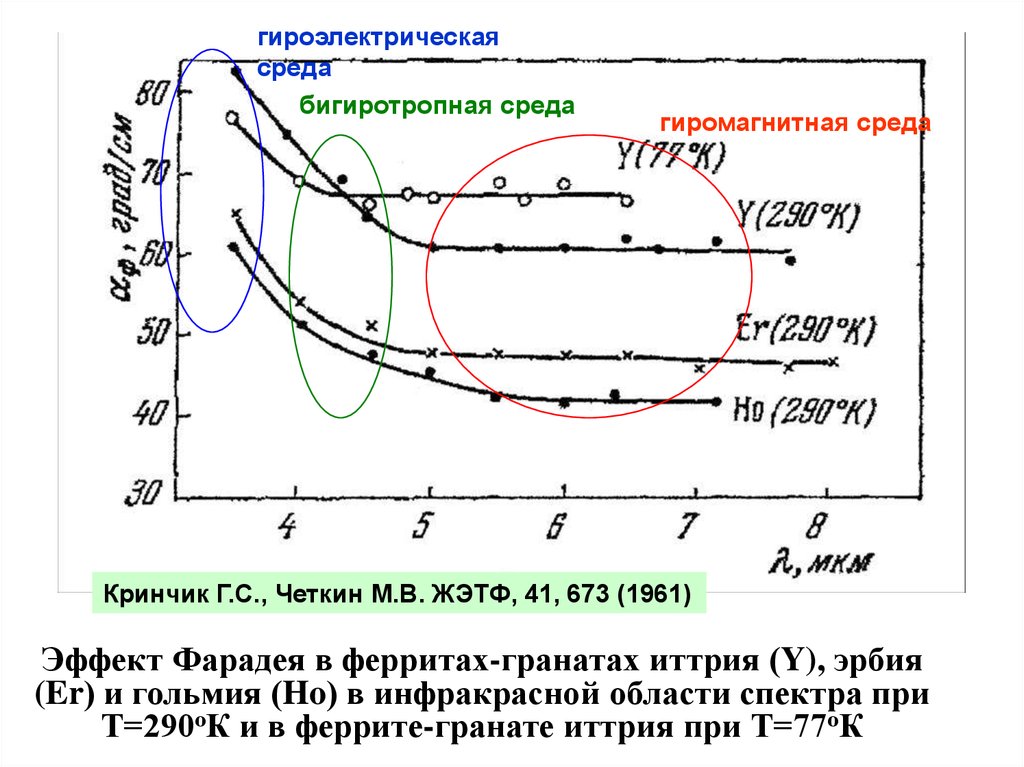
гироэлектрическаясреда
бигиротропная среда
гиромагнитная среда
Кринчик Г.С., Четкин М.В. ЖЭТФ, 41, 673 (1961)
Эффект Фарадея в ферритах-гранатах иттрия (Y), эрбия
(Er) и гольмия (Ho) в инфракрасной области спектра при
Т=290оК и в феррите-гранате иттрия при Т=77оК
27. Продольные эффекты.
n1, 2 (1 (Q' Q))2
Нельзя разделить вклады тензоров [ε] и [μ]
28. Однородная система имеет решение, если ее определитель равен нулю
i Qi Q
0
0
n
0
0
0
0
n
n
n
0
n
i Q'
0
0
o
n
n
n
n
i Q'
n
0
0
0
o
n
n
0
0
29. Пусть α,β≠0, γ=0. (Поперечные эффекты.)
i Qi Q
0
0
n
n
n
0
0
0
0
n
n
n
0
n
i Q'
0
0
o
n
n
n
n
i Q '
n
0
0
0
o
0
0
0
30. α,β≠0, γ=0. (Поперечные эффекты.)
i Qi Q
0
0
0
0
0
0
0
0
0
0
0
0
n
n
o
n
n
n
i Q'
n i Q '
0
0
0
n
n
0
0
0
o
0
31.
22
1 получим уравнение:
Учитывая, что
n 4 n 2 o (1 Q'2 ) o (Q 2 1) o o (Q 2 1)(1 Q'2 ) 0
n1, 2
2
o (1 Q'2 ) o (1 Q 2 ) o (1 Q'2 ) o (1 Q 2 )
2
2
2
(
1
Q
'
)
2
2
o
n1 ns
o (1 Q'2 )
2
n2 n p
2
2 o (1 Q )
2
o (1 Q )
2
2
2
S – волна
(Hz=0, Hx, Hy≠0);
вектор Е ┴ плоскости
падения света
P – волна
(Hz≠0, Hx, Hy=0),
Е ║ плоскости
падения света
32. Вектор Е в s- и p- волне
33. Показатели преломления
Для продольных эффектовn1, 2 (1 (Q' Q))
2
Для поперечных эффектов
ns o (1 Q' )
2
2
n p o (1 Q )
2
2
34.
Магнитооптические эффектысуществует только при
совместном влиянии обменного и
спин-орбитального
взаимодействия
35. Продольные и поперечные магнитооптические эффекты.
• Распространение электромагнитной волныв среде. Уравнения Максвелла
• Показатель преломления при продольном
распространении волны
Гироэлектрическая, гиромагнитная и
бигиротропная среды
Частотно независимый эффект Фарадея
• Показатель преломления при поперечном
распространении волны



















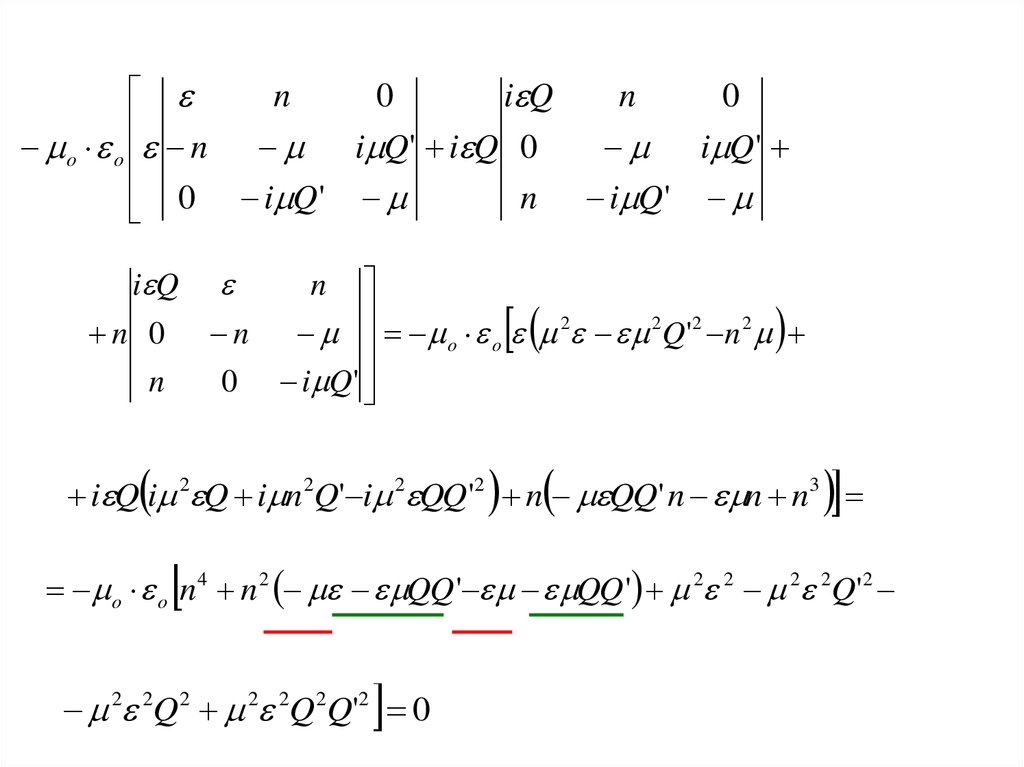













 Физика
Физика








