Цифровые фильтры

1. Тема: Цифровые фильтры.

Кафедра Радиоэлектроники.
Преподаватель:
Лазаренко
Сергей Валерьевич.
Радиотехнические цепи и сигналы. Лекция 24.

2.

Учебные вопросы:
1. Трансверсальный цифровой
фильтр.
2. Рекурсивный цифровой фильтр.
Радиотехнические цепи и сигналы. Лекция 24.

3.

1. Трансверсальный цифровой фильтр.
Физически осуществимые цифровые фильтры, которые работают в реальном
масштабе времени, для формирования выходного сигнала в i-тый дискретный
момент времени могут использовать следующие данные:
1) значение xi входного сигнала в момент i-того отсчета, а также некоторое число
"прошлых" входных отсчетов xi-1, xi-2, ..., xi-m;
2) некоторое число предшествующих отсчетов выходного сигнала yi-1, yi-2, ..., yi-n.
Так принято называть фильтры, не использующие для формирования выходного
сигнала в i-тый момент времени его предыдущие отсчеты, т.е. фильтры,
работающие в соответствии с алгоритмом:
y i a0 xi a1 xi 1 a 2 xi 2 ... a m xi m
(1)
где a0, a1,…, am- последовательность коэффициентов.
Применив Z-преобразование к обеим частям выражения (1), получим
Y ( z ) (a0 a1 z 1 a2 z 2 ... am z m ) X ( z )
Радиотехнические цепи и сигналы. Лекция 24.

4.

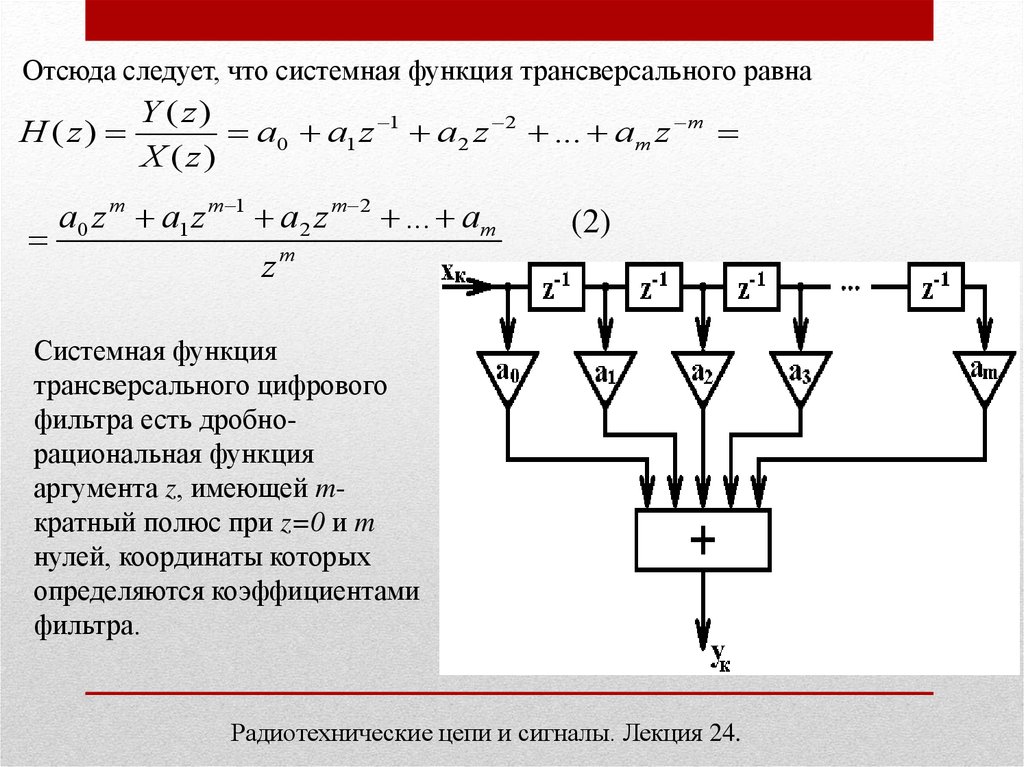
Отсюда следует, что системная функция трансверсального равна
Y ( z)
H ( z)
a0 a1 z 1 a2 z 2 ... am z m
X ( z)
a0 z m a1 z m 1 a2 z m 2 ... am
zm
(2)
Системная функция
трансверсального цифрового
фильтра есть дробнорациональная функция
аргумента z, имеющей mкратный полюс при z=0 и m
нулей, координаты которых
определяются коэффициентами
фильтра.
Радиотехнические цепи и сигналы. Лекция 24.

5.

Комплексный коэффициент передачи цифрового фильтра получается из
системной функции заменой аргумента z на ejɷ∆. Следовательно, получим:
K ( ) a0 a1e j a2 e 2 j ... a m z mj
На основе задания комплексного коэффициента передачи может быть реализован
один из алгоритмов цифровой фильтрации непрерывного сигнала:
1) производится дискретизация непрерывного входного сигнала;
2) определяется дискретное преобразование Фурье (в том числе с
использованием алгоритма быстрого преобразования);
3) перемножением комплексных коэффициентов дискретного ряда Фурье
входного сигнала и значений комплексного коэффициента передачи цифрового
фильтра определяется дискретное преобразование выходного сигнала;
4) путем использования обратного дискретного преобразования Фурье
определяется выходная последовательность, которая затем может быть
преобразована в непрерывный сигнал.
Прямая подстановка системной функции трансверсального цифрового фильтра
(2) в выражение (3) с учетом соотношений (4)...(6) дает следующий результат:
hk (a0 , a1 , a2 , ..., am )
Радиотехнические цепи и сигналы. Лекция 24.

6.

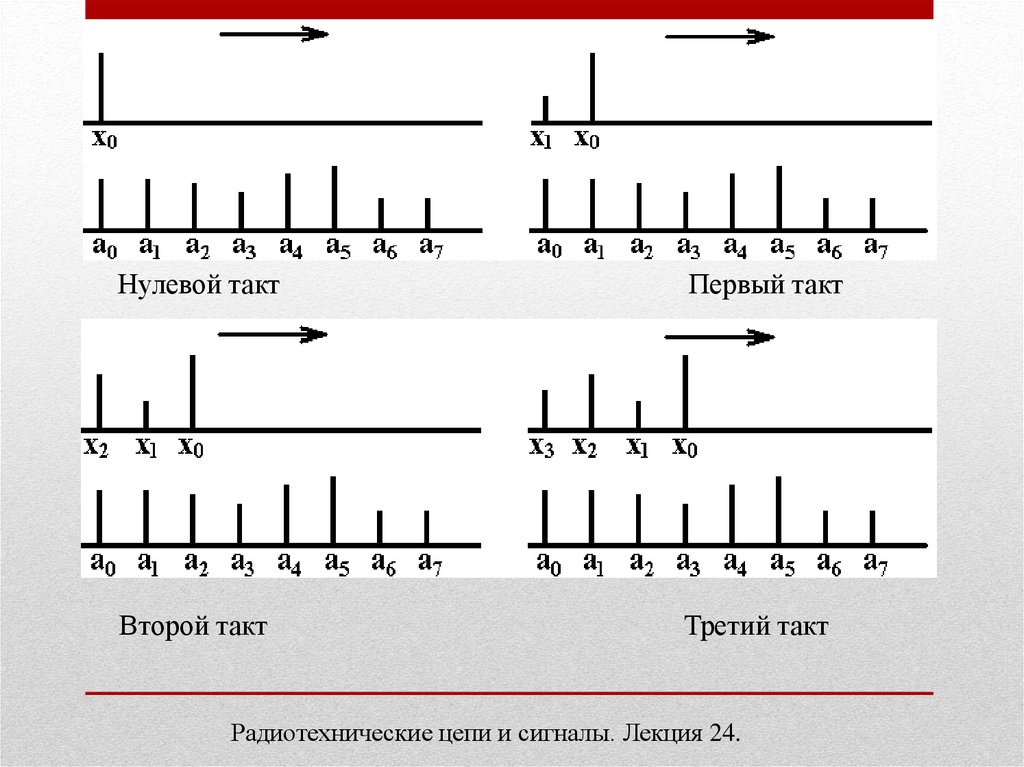
Нулевой такт
Первый такт
Второй такт
Третий такт
Радиотехнические цепи и сигналы. Лекция 24.

7.

Из рассмотрения рисунков видно, что
y 0 x0 a 0
y1 x0 a1 x1 a0
y 2, x0 a2 x1 a1 x2 a0
y 2 x0 a3 x1 a2 x2 a1 x3 a0 и т.д.
В общем случае
m
y m x0 am x1 am 1 x2 a m 2 ... xm a0 xk a m k
k 0
Трансверсальный фильтр первого порядка
Входная последовательность фильтра
определяется выражением
y m a 0 x m a1 x m 1
Следовательно, импульсная характеристика
равна
hk (a0 , a1 )
Системная функция такого фильтра
H ( z ) a0 a1 z 1
Радиотехнические цепи и сигналы. Лекция 24.
(4)

8.

Kомплексный коэффициент передачи
K ( ) a0 a1e j
Очень просто найти выражение для АЧХ фильтра.
K ( ) K ( ) a0 a1 cos ja1 sin a02 a12 2a0 a1 cos
При a0=a1=1 получаем
K ( ) 2 2 cos 2 cos
2
На частоте ɷ=П/∆ АЧХ обращается в нуль, и данный фильтр может выступать в
качестве режекторного.
При a0=1,a1=-1 имеем
K ( ) 2 2 cos 2 sin
2
и фильтр становится полосовым, средняя частота которого равна ɷ=П/∆ .
Радиотехнические цепи и сигналы. Лекция 24.

9.

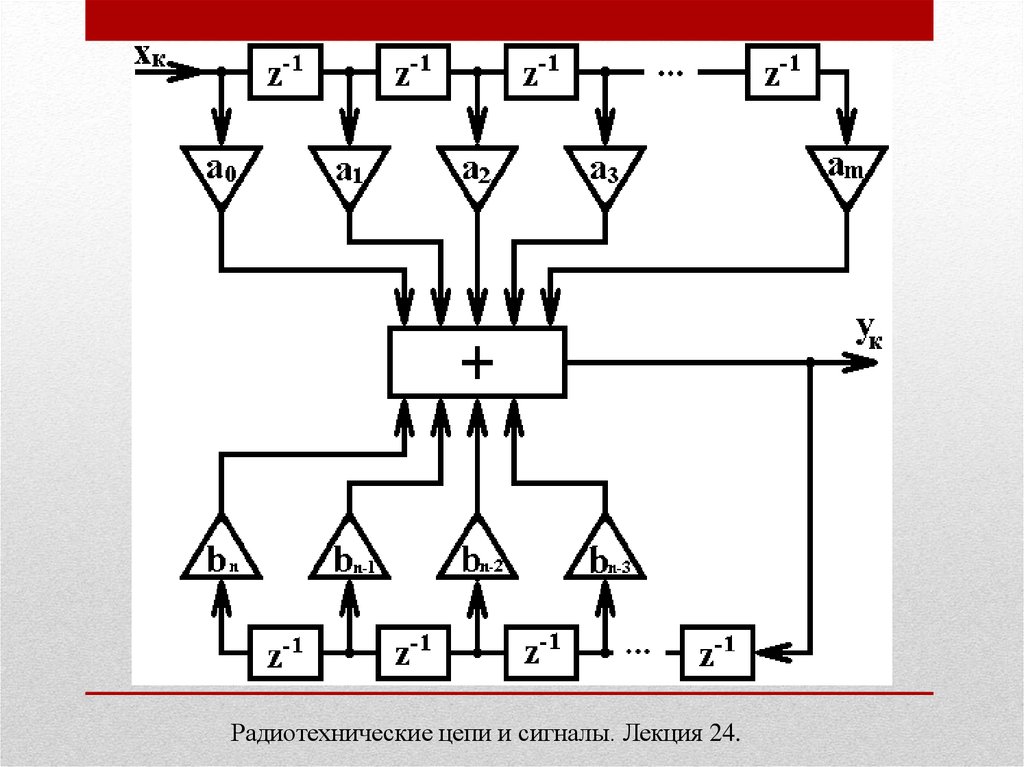
2. Рекурсивный цифровой фильтр.
Рекурсивный цифровой фильтр характерен тем, что для формирования k-того
выходного отсчета используются предыдущие значения не только входного, но и
выходного сигнала:
yk a0 xk a1 xk 1 ... am xk m b1 yk 1 b2 yk 2 ... bn yk n
(5)
Преобразуем уравнение (5), сгруппировав отсчеты выходного сигнала слева,
входного - справа:
y k b1 y k 1 b2 y k 2 ... bn y k n a0 xk a1 xk 1 ... am xk m
(6)
Найдем z-преобразование от обеих частей уравнения
Y ( z )(1 b1 z 1 ... bn z n ) X ( z )( a0 a1 z 1 ... a m z m )
(7)
и получим выражение для системной функции рекурсивного цифрового фильтра
Y ( z ) a0 a1 z 1 ... a m z m a0 z n a1 z n 1 ... a m z n m
H ( z)
1
n
X ( z)
1 b1 z ... bn z
z n b1 z n 1 ... bn
Радиотехнические цепи и сигналы. Лекция 24.
(8)

10.

Радиотехнические цепи и сигналы. Лекция 24.

11.

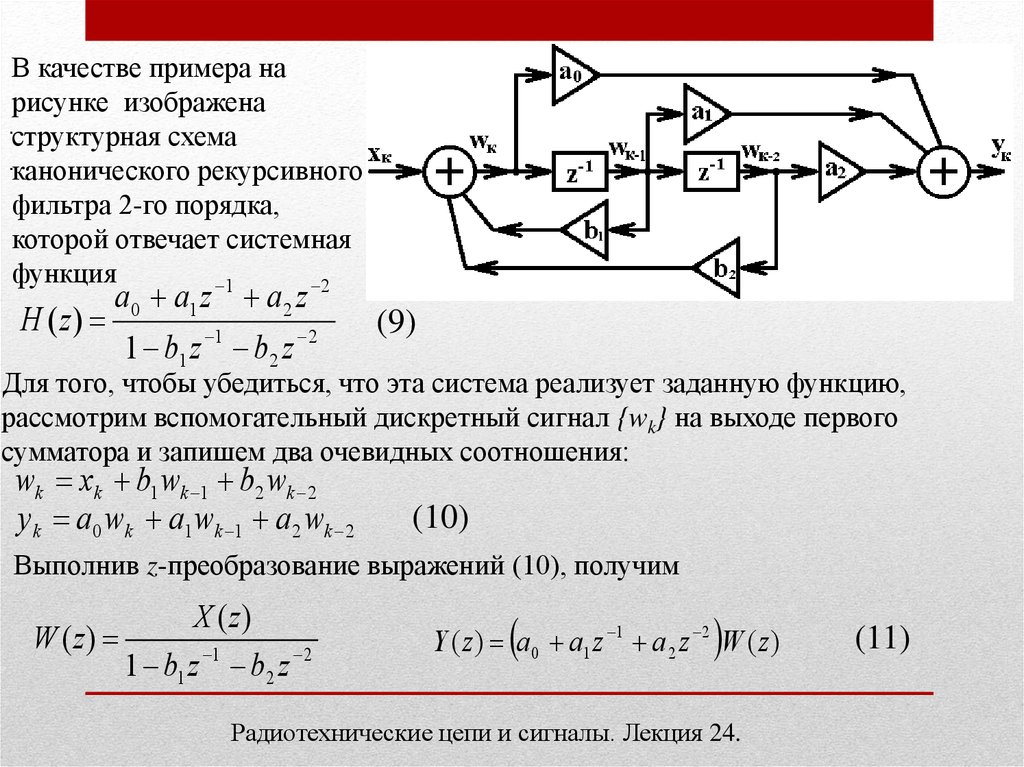
В качестве примера на
рисунке изображена
.
структурная схема
.канонического рекурсивного
фильтра 2-го порядка,
которой отвечает системная
функция
1
2
a 0 a1 z a 2 z
H ( z)
1 b1 z 1 b2 z 2
(9)
Для того, чтобы убедиться, что эта система реализует заданную функцию,
рассмотрим вспомогательный дискретный сигнал {wk} на выходе первого
сумматора и запишем два очевидных соотношения:
wk xk b1 wk 1 b2 wk 2
y k a0 wk a1 wk 1 a 2 wk 2
(10)
Выполнив z-преобразование выражений (10), получим
W ( z)
X ( z)
1 b1 z 1 b2 z 2
Y ( z ) a 0 a1 z 1 a 2 z 2 W ( z )
Радиотехнические цепи и сигналы. Лекция 24.
(11)

12.

Характерная черта, отличающая рекурсивный цифровой фильтр, состоит в том,
что из-за наличия обратной связи его импульсная характеристика имеет вид
неограниченно-протяженной последовательности. Покажем это на примере
простейшего фильтра первого порядка, системная функция которого описывается
выражением
H ( z)
az
a
1 b z 1 z b
Импульсная характеристика, как известно, есть обратное z - преобразование от
системной функции, поэтому можно записать
a z m 1
1
1 a zm
gm
z dz
dz
2 j z b
2 j z b
Вначале найдем g0:
g0
1
a
dz
2 j z b
Произведя замену z-b=y, получим
1 a
g0
dy a
2 j y
Радиотехнические цепи и сигналы. Лекция 24.

13.

Аналогично найдем g1
az
1
1 a ( y b)
g1
dz
dz ab
2 j z b
2 j
y
Не трудно убедиться в том, что g2=ab2, g3=ab2 и т.д. Искомая
импульсная характеристика представляет собой геометрическую
прогрессию. Очевидно, что для того, чтобы прогрессия была
убывающей (чтобы фильтр был устойчивым), необходимо
выполнения условия b<1.
Комплексный коэффициент передачи рекурсивного цифрового
фильтра первого порядка получим на основе системной функции
путем замены z на ejɷ∆:
a
K ( )
1 b e j
Отсюда не трудно найти АЧХ
a
a
K ( )
1 b cos j sin
1 b 2 2b cos
Радиотехнические цепи и сигналы. Лекция 24.