Пирамида. Элементы пирамиды

1.

ПИРАМИДА

2.

Определение: многогранник, составленный из n
-угольника A1A2…An и n треугольников
называется пирамидой.
Обозначение: РA1A2…An – называется n-угольной
пирамидой.

3.

Элементы пирамиды
Многоугольник
A1A2…An
называется
основанием
пирамиды.
Треугольники A1PA2 , A2PA3 , … ,
AnPA1 – боковыми гранями
пирамиды.
Точка P называется вершиной пирамиды.
Отрезки PA1, PA2, …, PAn - её боковыми ребрами.

4.

Определение:
перпендикуляр,
проведенный из вершины
пирамиды к плоскости
основания, называется
высотой пирамиды.
PH ( A1 A2 A3 )

5.

Правильная пирамида
Определение: пирамида
называется правильной,
если её основание –
правильный
многоугольник, а отрезок,
соединяющий вершину
пирамиды с центром
основания, является её
высотой.

6.

Определение: высота боковой грани правильной
пирамиды, проведенная из её вершины
называется апофемой.
P
P
N
K
M
M
O
N
РМ, PN, РК - апофемы
O
K
L
PL, PK, PN, PM - апофемы

7.

Свойства правильной пирамиды
1. Все боковые ребра правильной
пирамиды равны.
2. Боковые грани
правильной
пирамиды являются равными
равнобедренными
треугольниками.
3. Все
апофемы
правильной
пирамиды равны друг другу.

8.

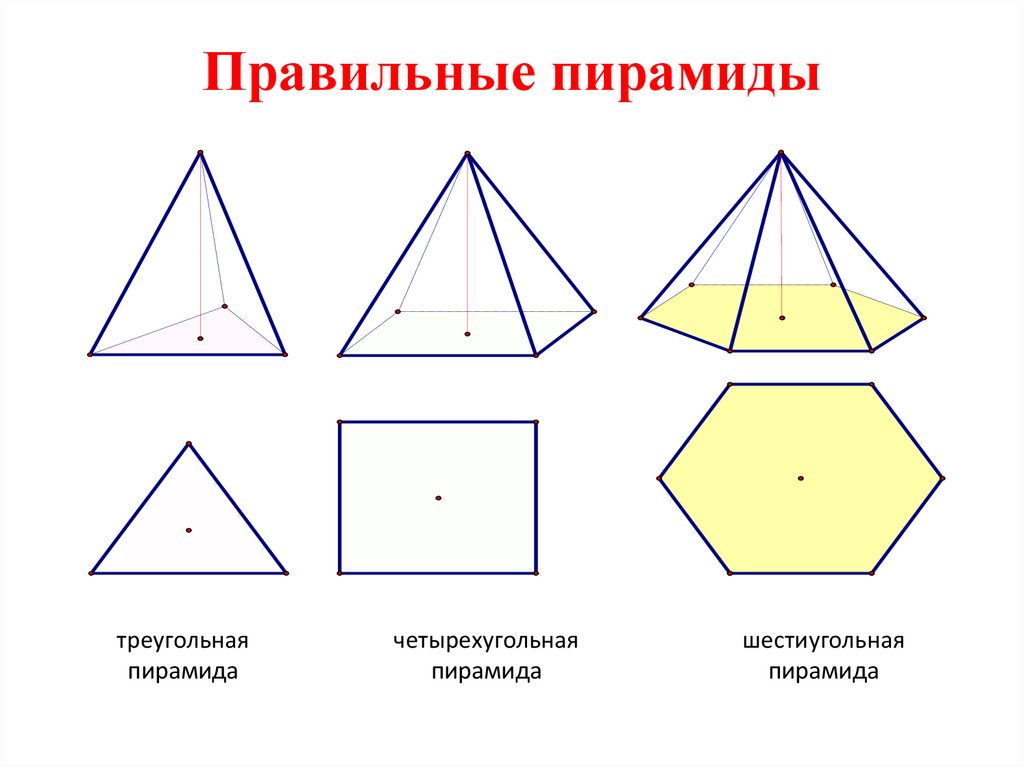
Правильные пирамиды
треугольная
пирамида
четырехугольная
пирамида
шестиугольная
пирамида

9.

Площадь поверхности пирамиды
Площадью полной поверхности (Sполн ) пирамиды
называется сумма площадей всех её граней.
Площадью боковой поверхности ( Sбок ) пирамиды
называется сумма площадей её боковых граней.
Sполн Sбок Sосн

10.

Теорема о площади боковой поверхности
правильной пирамиды
Теорема.
Площадь боковой
поверхности
правильной
пирамиды
равна
половине
произведения
периметра
основания
на
апофему.
1
Sбок Pосн d
2

11.

Усеченная пирамида
Основания усеченной пирамиды
Вn
А1А2А3…Аn, В1В2В3…Вn
В1
В2
В3
Боковые грани усеченной пирамиды
А1В1В2А2, А2В2В3А3,…, А1В1ВnАn
Аn
Боковые ребра усеченной
пирамиды
А1
А1В1, А2В2, А3В3, …, АnВn
А2
А3

12.

Определение:
перпендикуляр,
проведенный из какойнибудь точки одного
основания к плоскости
другого основания,
называется высотой
усеченной пирамиды.
В5
В1
В4
С
В2
В3
А5
А4
Н
А1
А2
А3
Отрезок СН является
высотой усеченной
пирамиды.

13.

Все боковые грани усеченной
пирамиды - трапеции

14.

Определение: усеченная пирамида называется
правильной, если она получена сечением
правильной пирамиды плоскостью, параллельной
основанию.

15.

Площадь поверхности усеченной
пирамиды
Площадью полной поверхности ( Sполн ) усеченной
пирамиды называется сумма площадей всех её
граней.
Площадью боковой поверхности ( Sбок ) усеченной
пирамиды называется сумма площадей её боковых
граней.
Sполн Sбок Sосн1 Sосн 2

16.

Теорема о площади боковой поверхности
правильной усеченной пирамиды
Теорема:
площадь
боковой
поверхности
правильной
усеченной
пирамиды
равна
произведению полусуммы периметров оснований
на апофему.
1
Sбок Pосн1 Pосн 2 d
2

17.

Объем пирамиды
Теорема: объем пирамиды
равен одной трети
произведения площади
основания на высоту:
1
V Sосн h
3

18.

Объем усеченной пирамиды
Теорема: объем усеченной
пирамиды, высота которой
равна h, а площади оснований
равны S1 и S2, вычисляются по
формуле:
1
V h S1 S2 S1 S2
3

19.

СПАСИБО ЗА ВНИМАНИЕ!