Похожие презентации:
Пространственные фигуры. Площадь, объем
1. Пространственные фигуры
Площадь, объем.2.
3.
D1C1
А1
B1
С
D
А
В
4.
Геометрическое тело или многогранник,состоящий из трёх пар равных параллелограммов лежащих в параллельных плоскостях, называется параллелепипедом
(Назвать вершины, рёбра, грани и их количество.)
5.
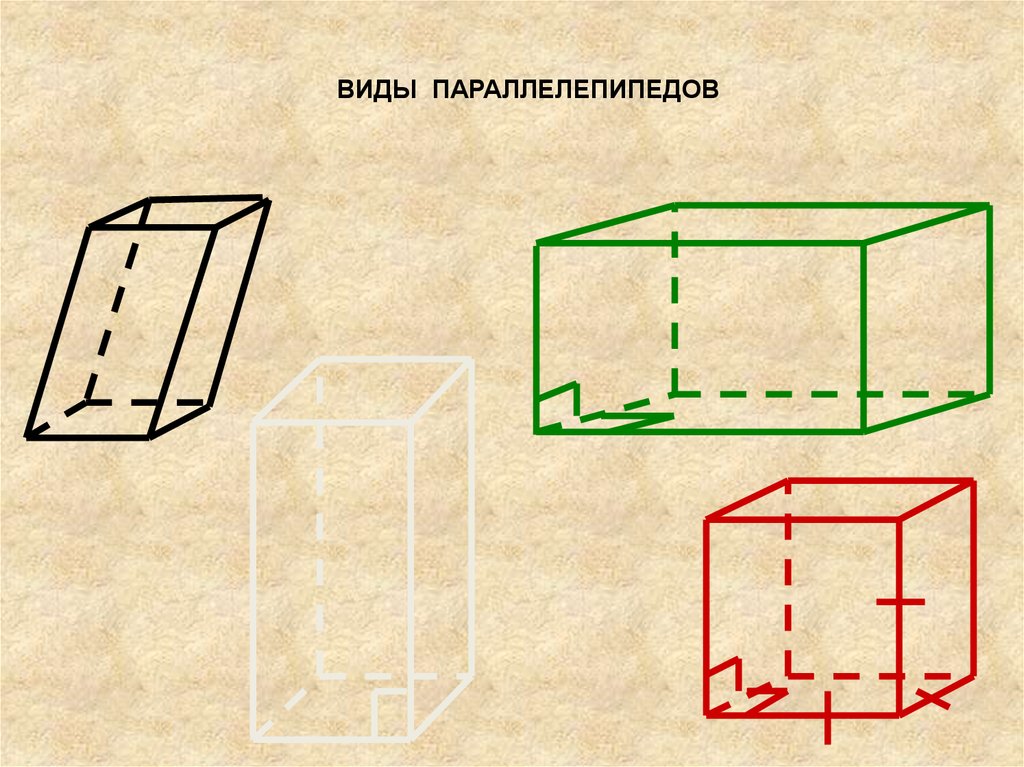
ВИДЫ ПАРАЛЛЕЛЕПИПЕДОВ6.
ПРЯМОЙ ПАРАЛЛЕЛЕПИПЕДПараллелепипед,
у которого боковые
стороны перпендикулярны основанию,
называется прямым.
7.
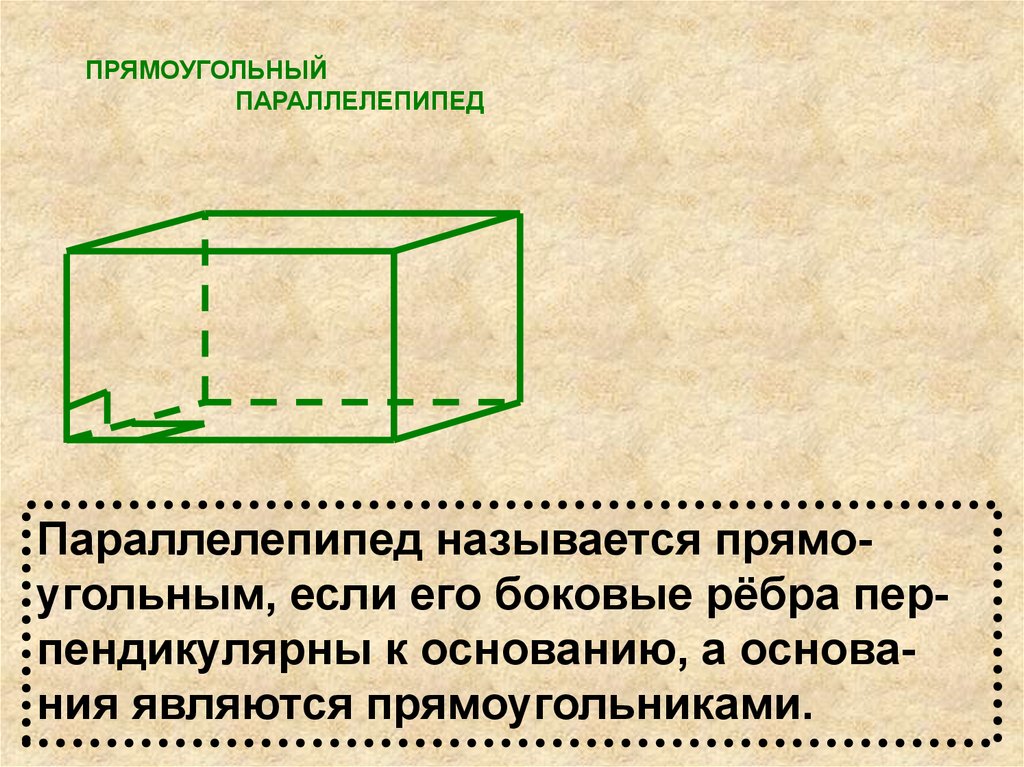
ПРЯМОУГОЛЬНЫЙПАРАЛЛЕЛЕПИПЕД
Параллелепипед называется прямоугольным, если его боковые рёбра перпендикулярны к основанию, а основания являются прямоугольниками.
8.
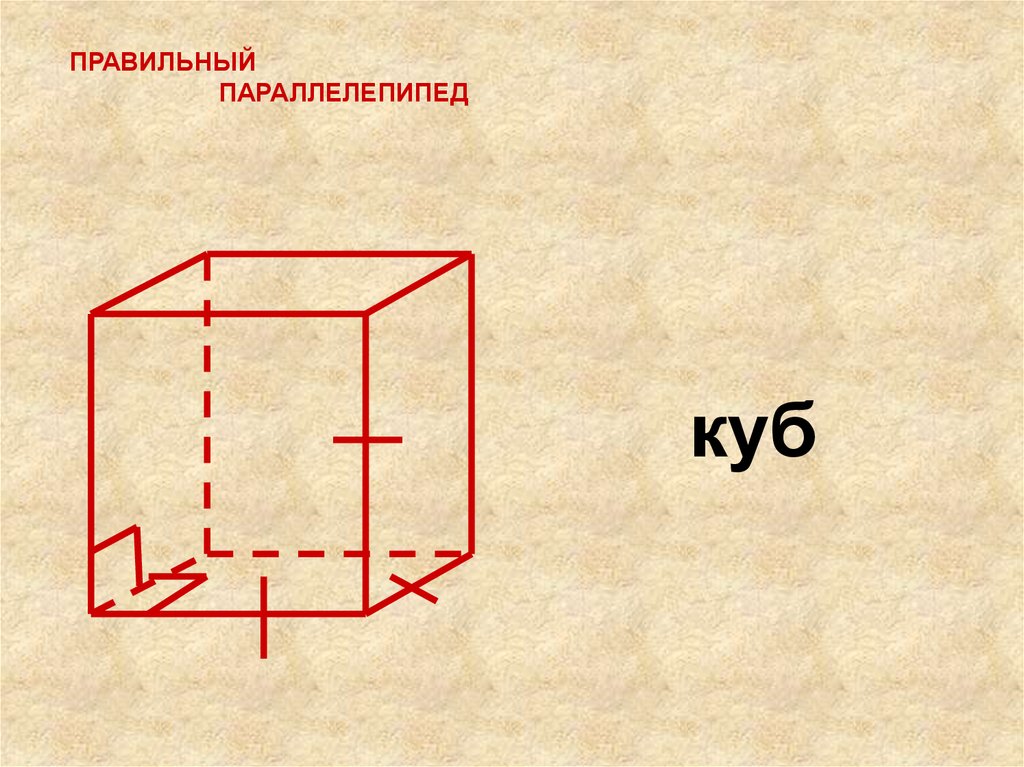
ПРАВИЛЬНЫЙПАРАЛЛЕЛЕПИПЕД
куб
9.
C1D1
B1
A1
D
А
С
В
1. В прямоугольном параллелепипеде
все шесть граней – прямоугольники.
2. Все двугранные углы прямоугольного параллелепипеда – прямые.
10.
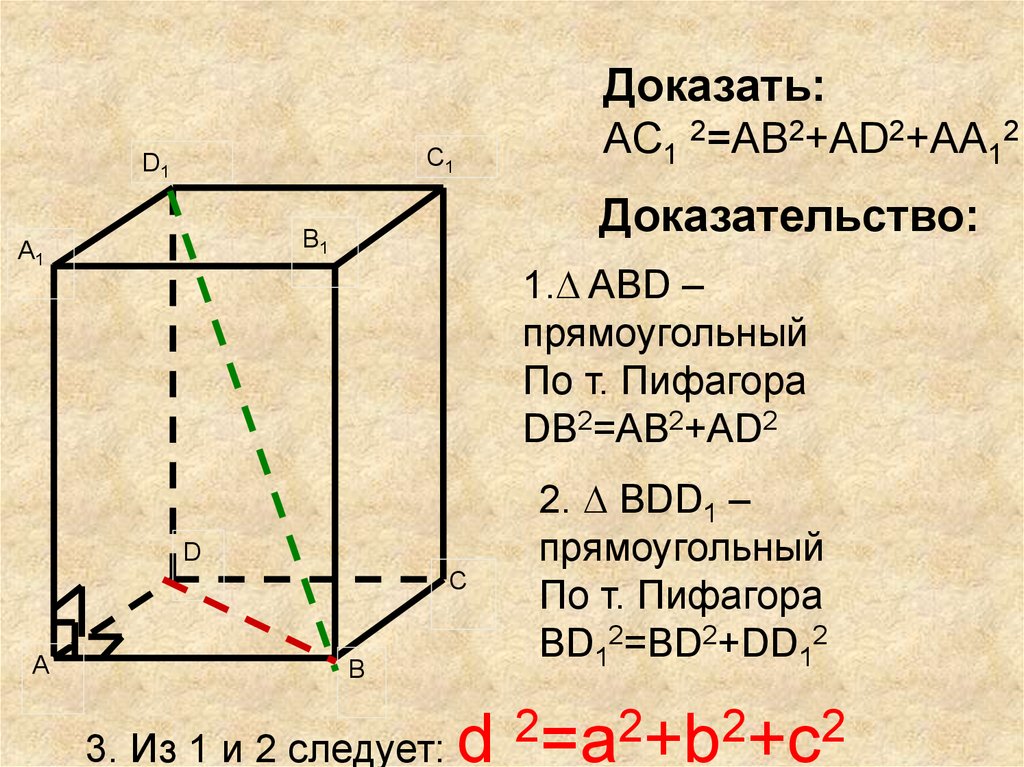
Доказать:AC1 2=AB2+AD2+AA12
C1
D1
Доказательство:
B1
A1
1. ABD –
прямоугольный
По т. Пифагора
DB2=AB2+AD2
D
С
А
В
3. Из 1 и 2 следует:
2. BDD1 –
прямоугольный
По т. Пифагора
BD12=BD2+DD12
d 2=a2+b2+c2
11. Площадь поверхности и объем
12. Призма
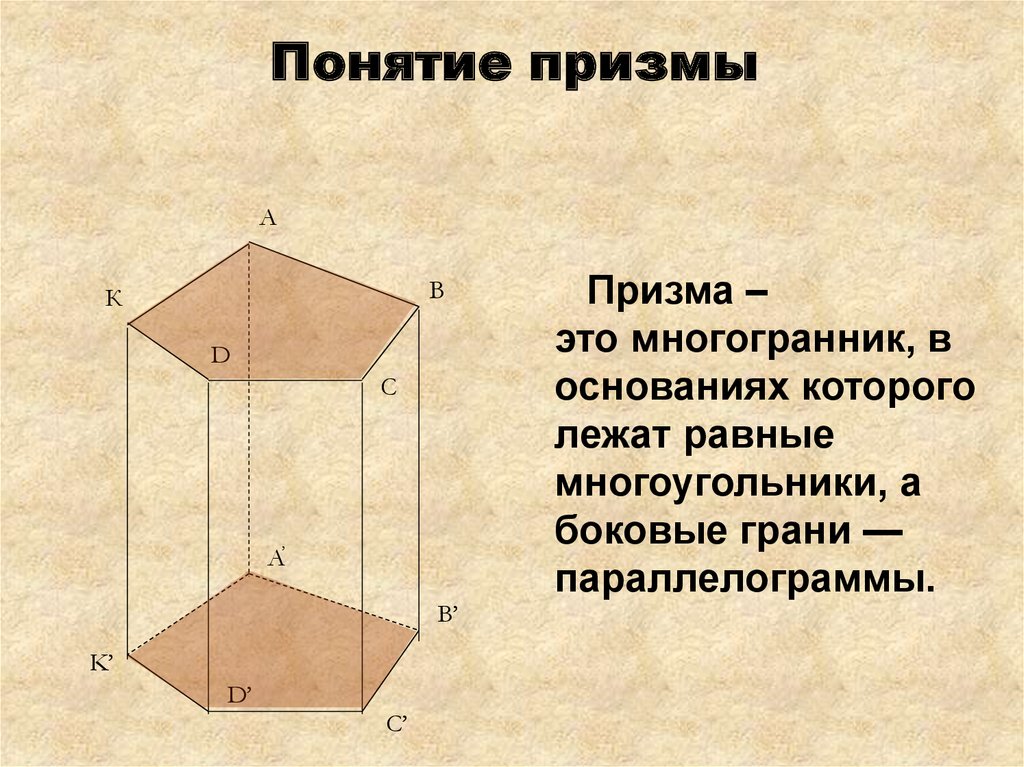
13. Понятие призмы
АВ
К
D
С
A’
B’
K’
D’
C’
Призма –
это многогранник, в
основаниях которого
лежат равные
многоугольники, а
боковые грани —
параллелограммы.
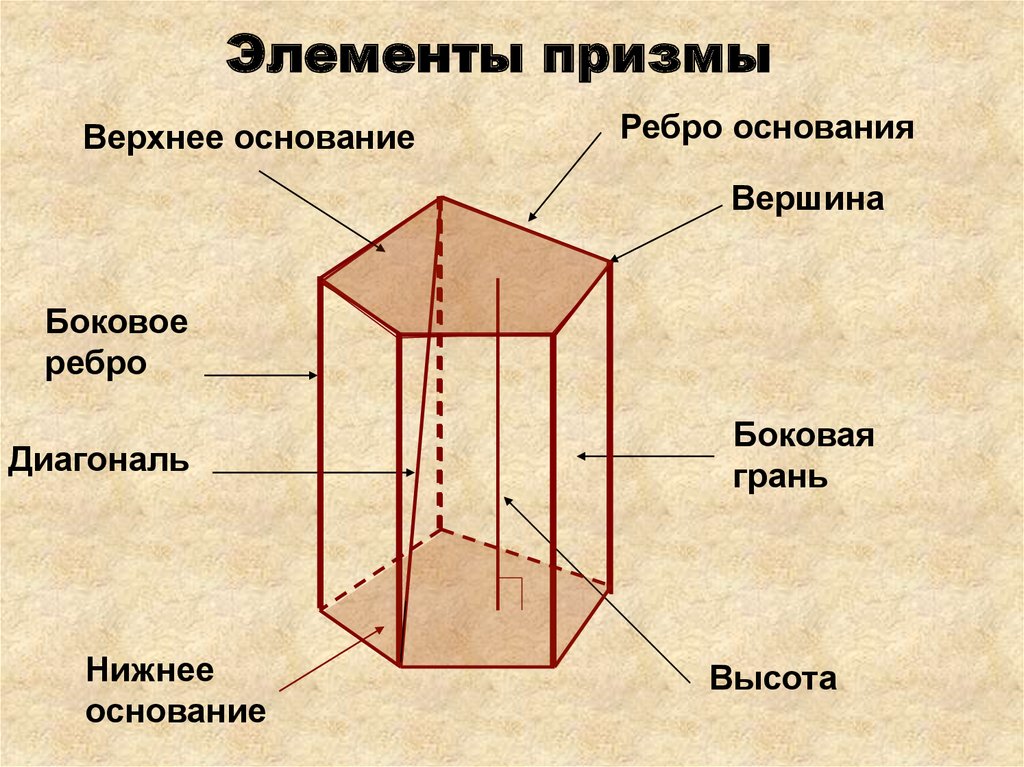
14. Элементы призмы
Верхнее основаниеРебро основания
Вершина
Боковое
ребро
Диагональ
Нижнее
основание
Боковая
грань
Высота
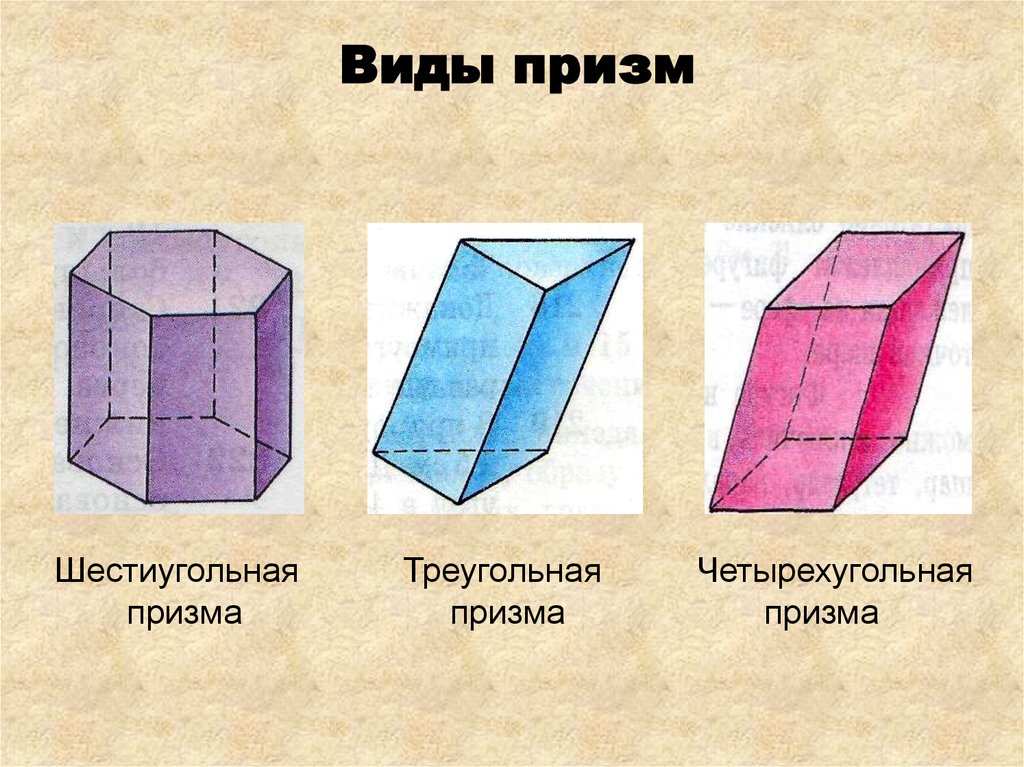
15. Виды призм
Шестиугольнаяпризма
Треугольная
призма
Четырехугольная
призма
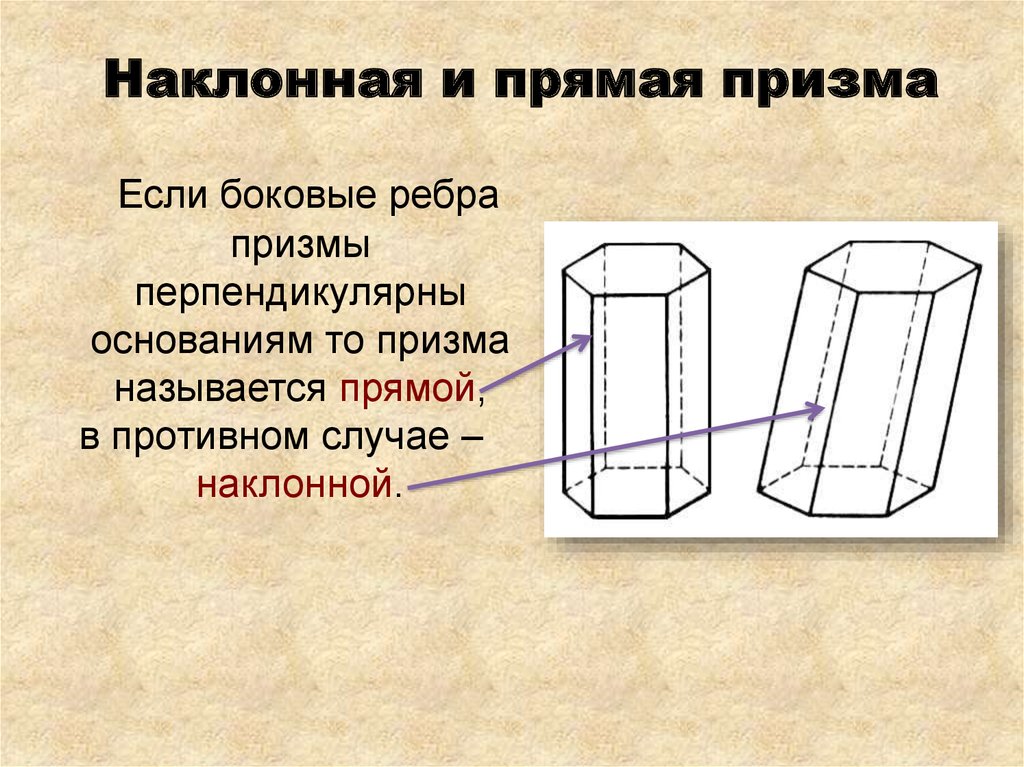
16. Наклонная и прямая призма
Если боковые ребрапризмы
перпендикулярны
основаниям то призма
называется прямой,
в противном случае –
наклонной.
17. Правильная призма
Призма называетсяправильной, если она
прямая и ее основания правильные
многоугольники.
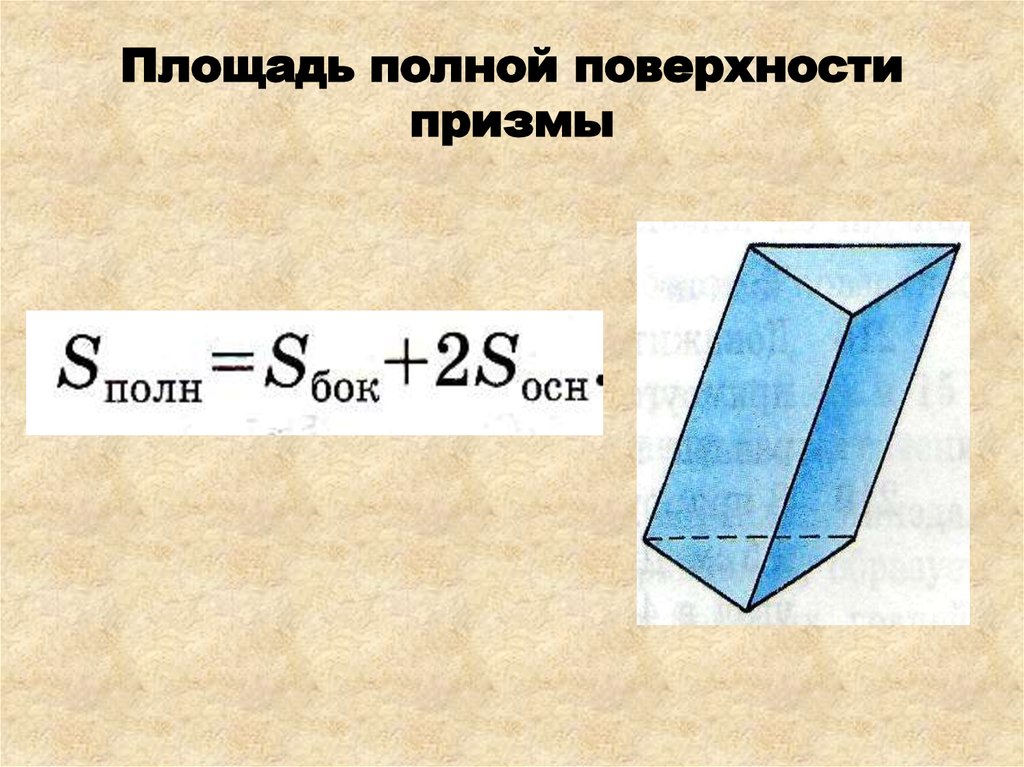
18. Площадь полной поверхности призмы
19. Площадь боковой поверхности призмы
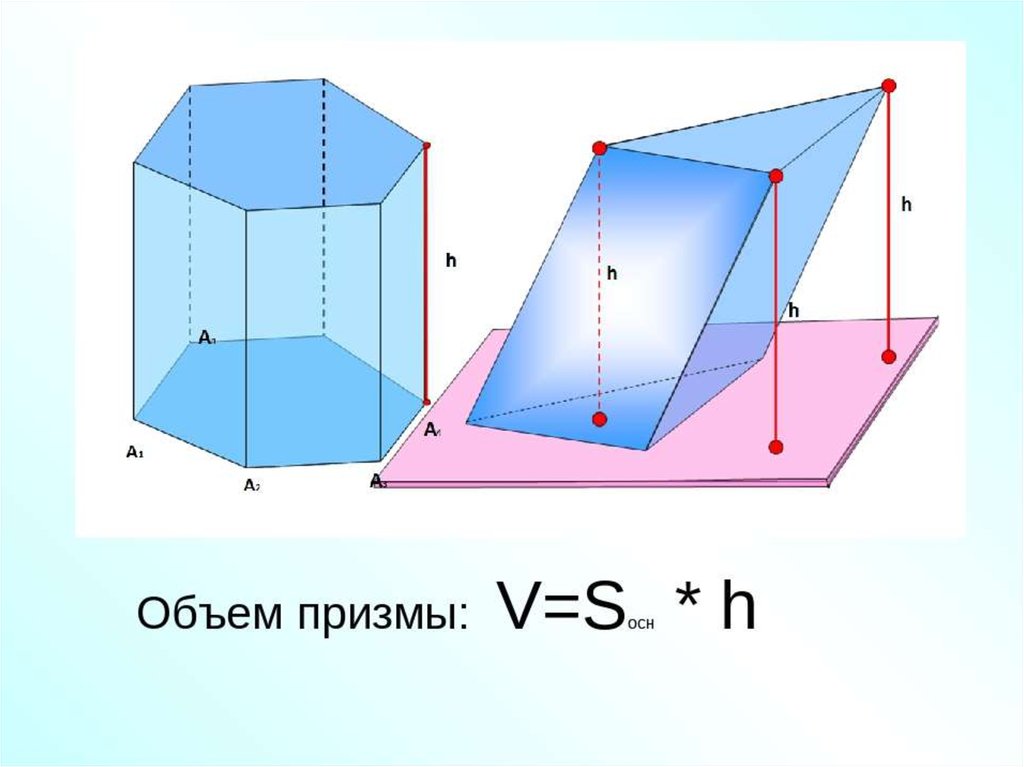
20. Объем призмы
21. Общие свойства призмы
1. Основания призмы равны2. Основания призмы лежат в
параллельных плоскостях
3. У призмы боковые рёбра параллельны и
равны
4. Любая боковая грань является
параллелограммом
22. Особые сечения призмы
Диагональное сечение– это сечение
проходящее через два
боковых ребра, не
принадлежащих одной
грани.
Перпендикулярное
сечение – это сечение,
проходящее
перпендикулярно
боковым ребрам.
23.
24.
Пирамида25.
Большая пирамида Хеопса26.
Пирамиды, созданныеприродой
27.
Современные здания28.
Опятьпирамида
29.
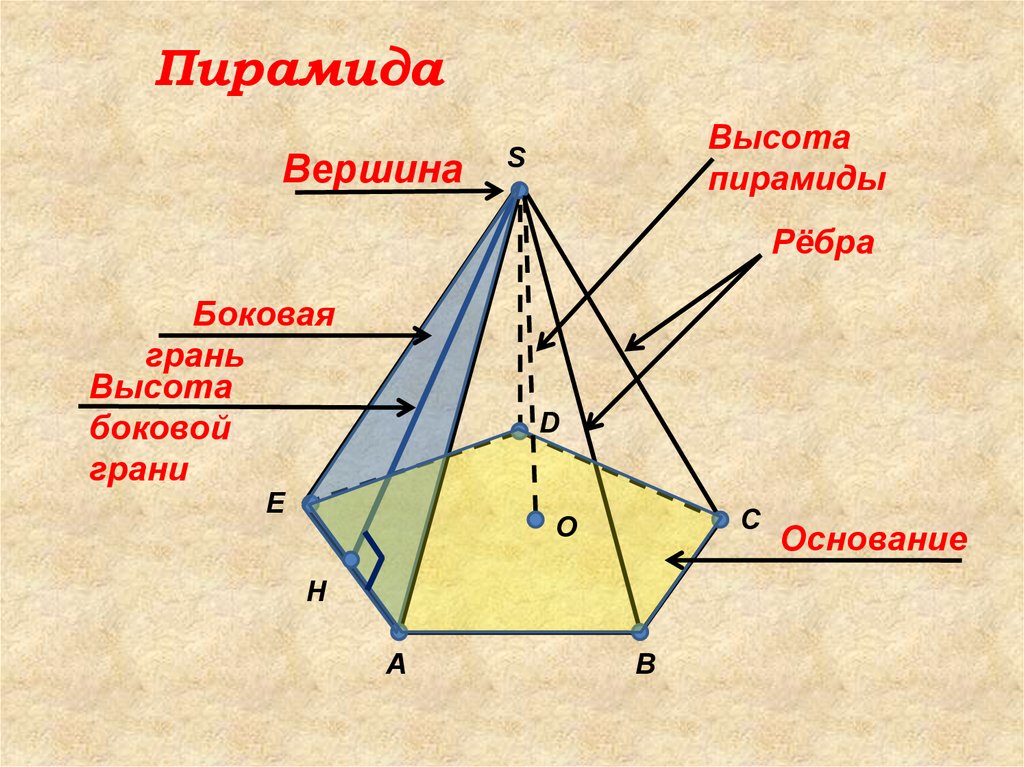
ПирамидаВершина
Высота
пирамиды
S
Рёбра
Боковая
грань
Высота
боковой
грани
D
E
C
O
H
A
B
Основание
30.
Виды пирамидM
S
Боковая
поверхность
B
C
D
A
C
A
B
Треугольная
пирамида
Четырёхугольная пирамида
31.
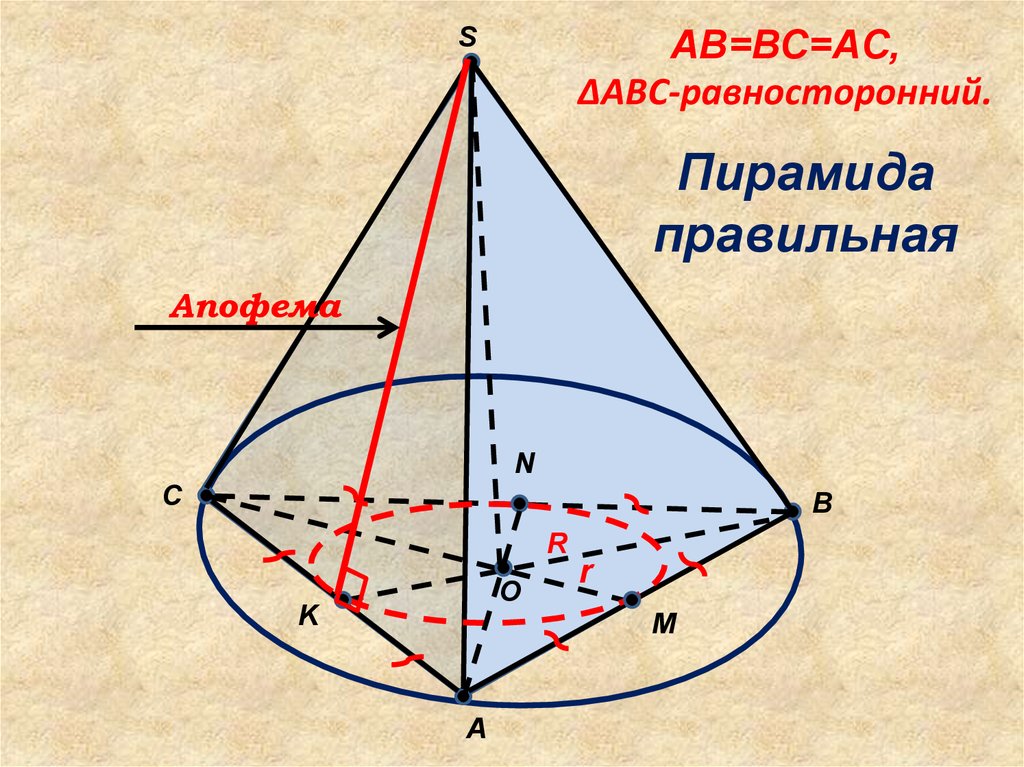
SAB=BC=AC,
∆ABC-равносторонний.
Пирамида
правильная
Апофема
N
C
B
R
O
K
r
M
A
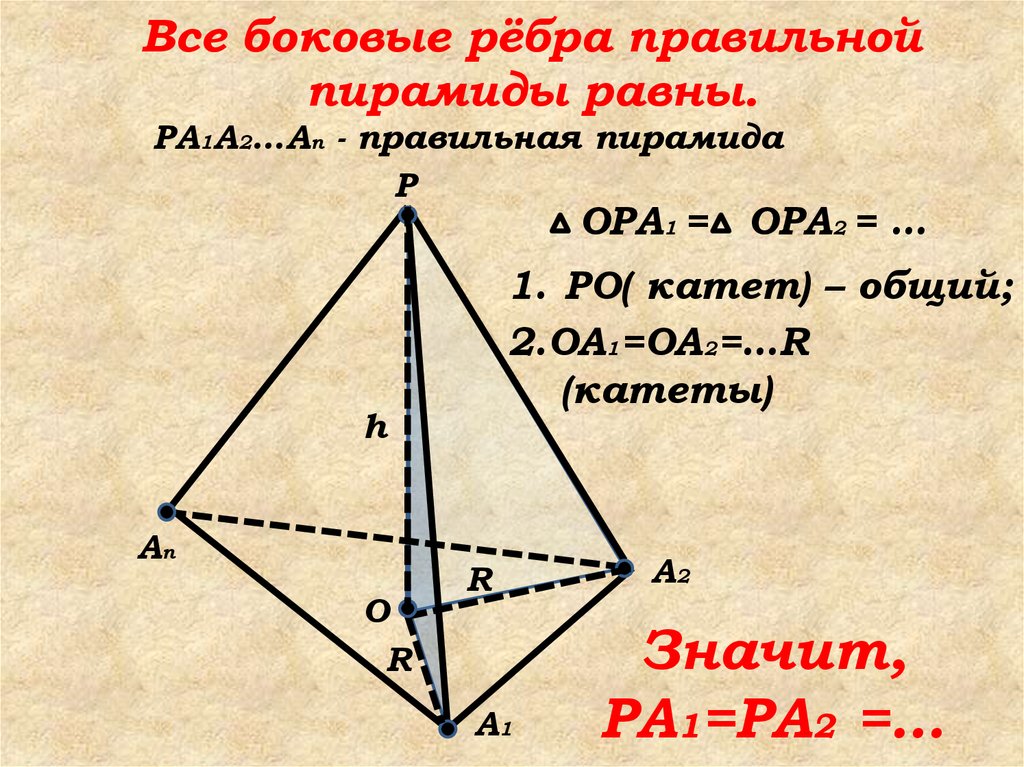
32. Все боковые рёбра правильной пирамиды равны.
PA1A2…An - правильная пирамидаP
OPA1 = OPA2 = …
1. PO( катет) – общий;
2.OA1=OA2=…R
(катеты)
h
An
O
R
R
A1
A2
Значит,
PA1=PA2 =…
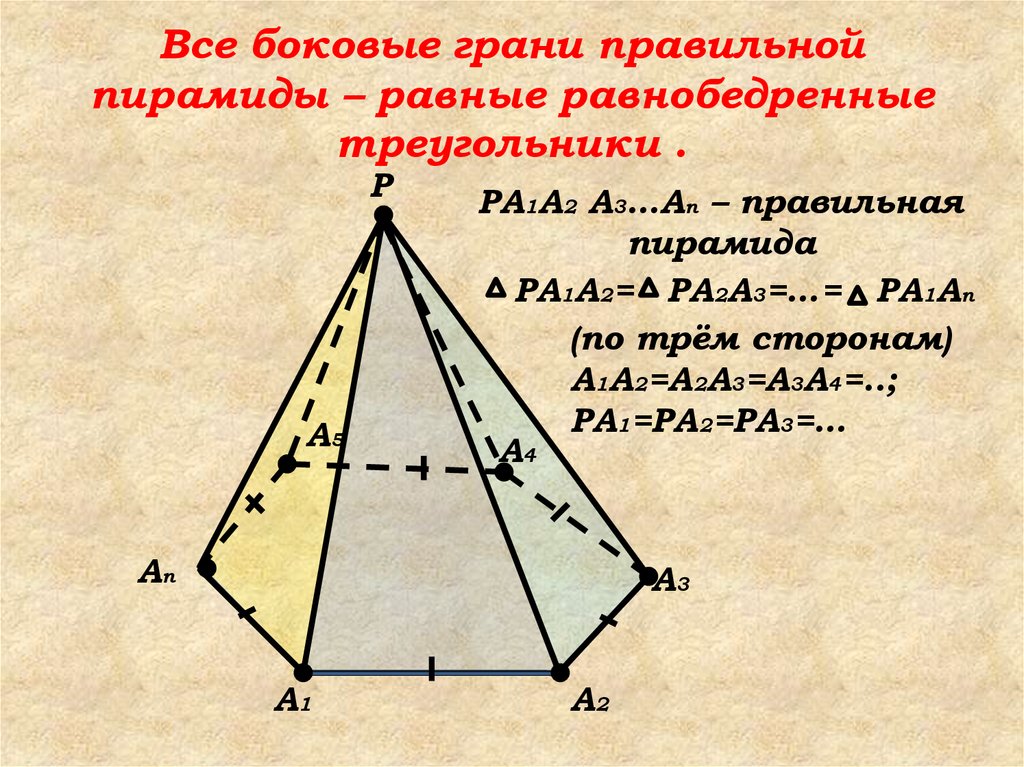
33. Все боковые грани правильной пирамиды – равные равнобедренные треугольники .
PA5
PA1A2 A3…An – правильная
пирамида
PA1A2= PA2A3=…= PA1An
(по трём сторонам)
A1A2=A2A3=A3A4=..;
PA1=PA2=PA3=…
A4
An
A3
A1
A2
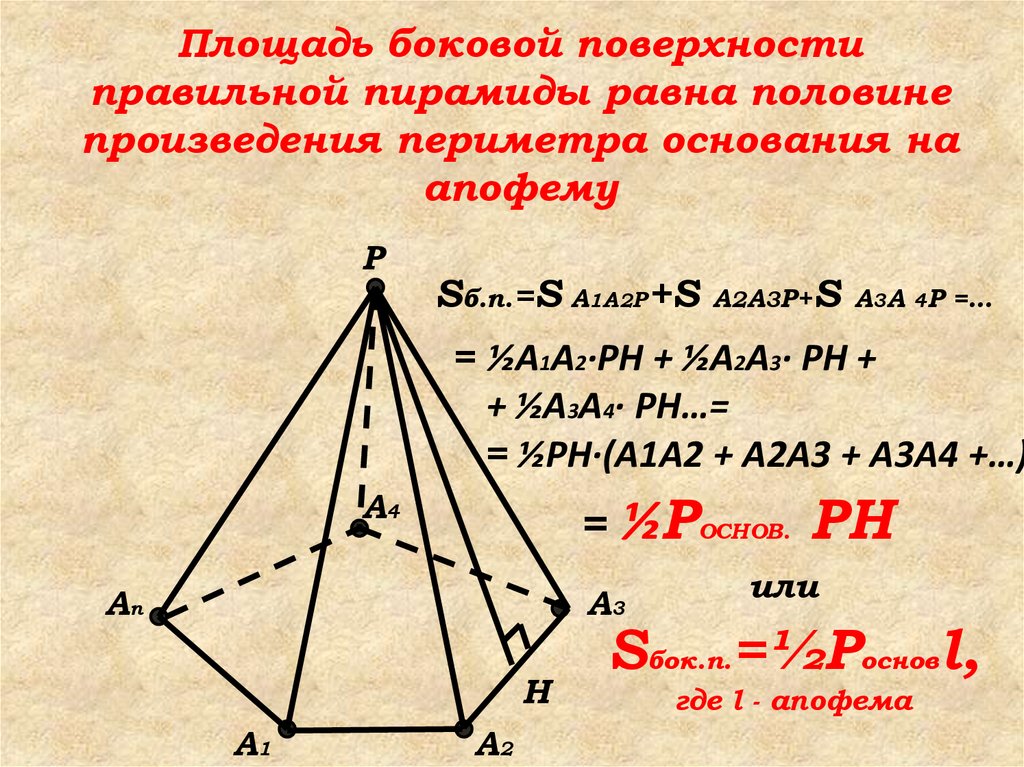
34. Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему
PSб.п.=S A1A2P+S
A2A3P+S A3A 4P =…
= ½A1A2·PH + ½A2A3· PH +
+ ½A3A4· PH…=
= ½PH·(A1A2 + A2A3 + A3A4 +…)
A4
=
An
½P
ОСНОВ.
A3
H
A1
A2
PH
или
Sбок.п.=½Pосновl,
где l - апофема
35.
36.
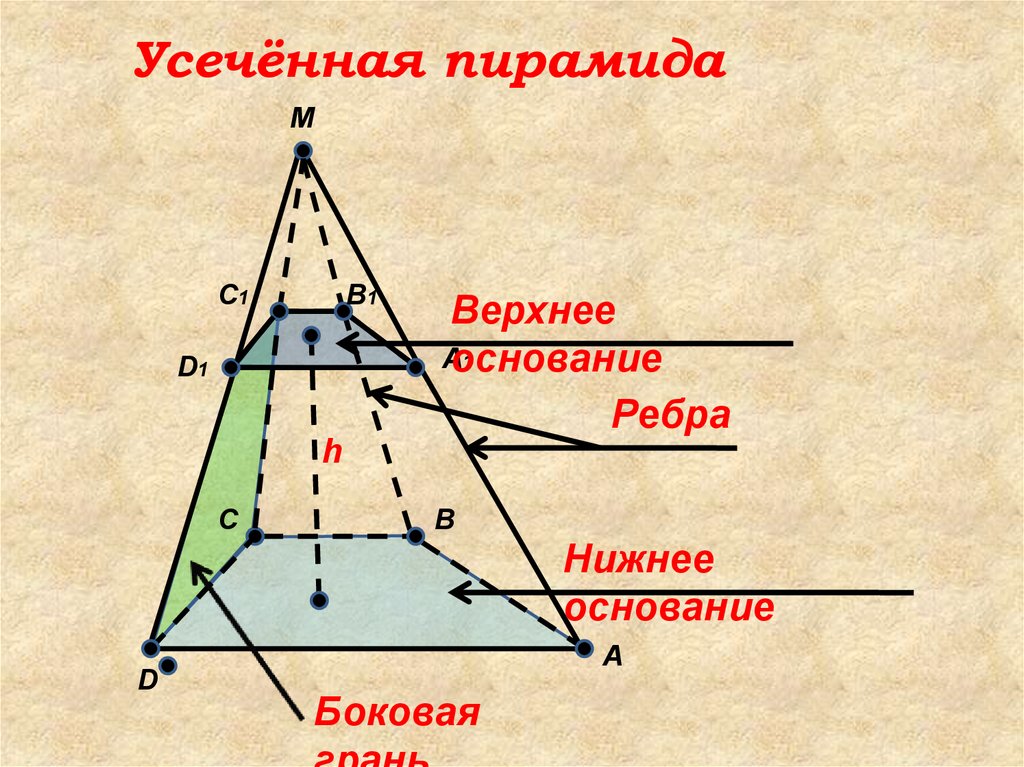
Усечённая пирамидаM
C1
B1
D1
Верхнее
Aоснование
1
Ребра
h
C
B
Нижнее
основание
D
A
Боковая




















 Математика
Математика








