Похожие презентации:
Решение тригонометрических уравнений
1. Решение тригонометрических уравнений
2. Содержание
Простейшиетригонометрические
уравнения
Простейшие
тригонометрические
неравенства
3. Простейшие тригонометрические уравнения
Определение арксинусаУравнение sin t = a
Определение арккосинуса
Уравнение cos t = a
Определение арктангенса
Уравнение tg t = a
Определение арккотангенса
Уравнение ctg t = a
Примеры
4. Определение арксинуса
Арксинусом числа а называетсятакой угол из промежутка [− 0,5π; 0,5π],
синус которого равен а, где lаl ≤ 1.
arcsin a = t , sin t = a
где t [− 0,5π; 0,5π]
а [− 1; 1]
аrcsin(- a) = -arcsina, а [− 1; 1]
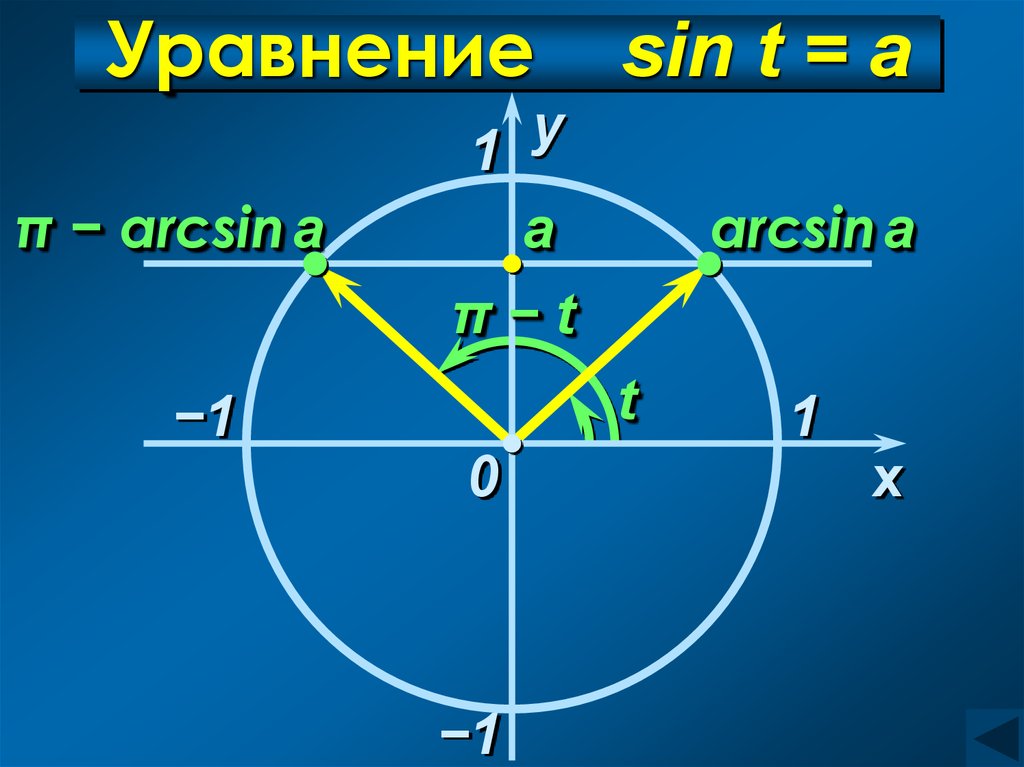
5. Уравнение sin t = а
Уравнениеπ − arcsin a
sin t = а
у
1
а
arcsin a
π−t
−1
t
0
−1
1
x
6.
Уравнениеsin t = а
C учетом периодичности:
t = arcsin a + 2πn, n Z
t = π − arcsin a + 2πn, n Z
Объединив в одну формулу:
t = (−1)n arcsin a + πn, n Z
Пример
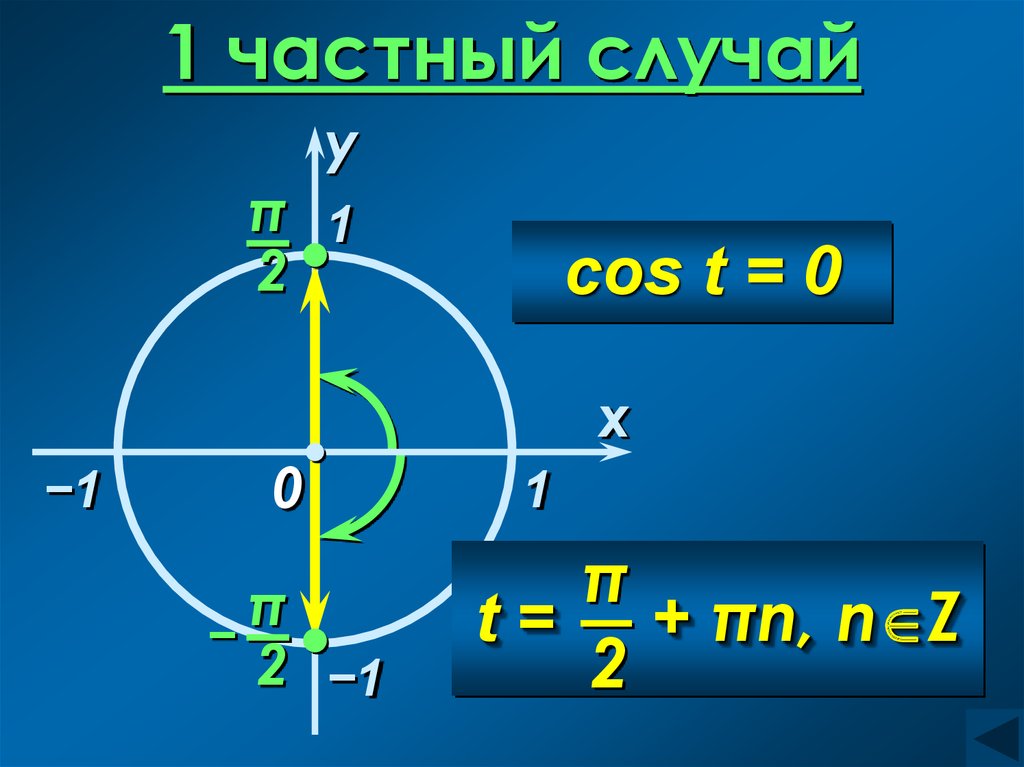
7.
1 частный случайy
1
−1
π
sin t = 0
1
0
x
0
t = πn, n Z
−1
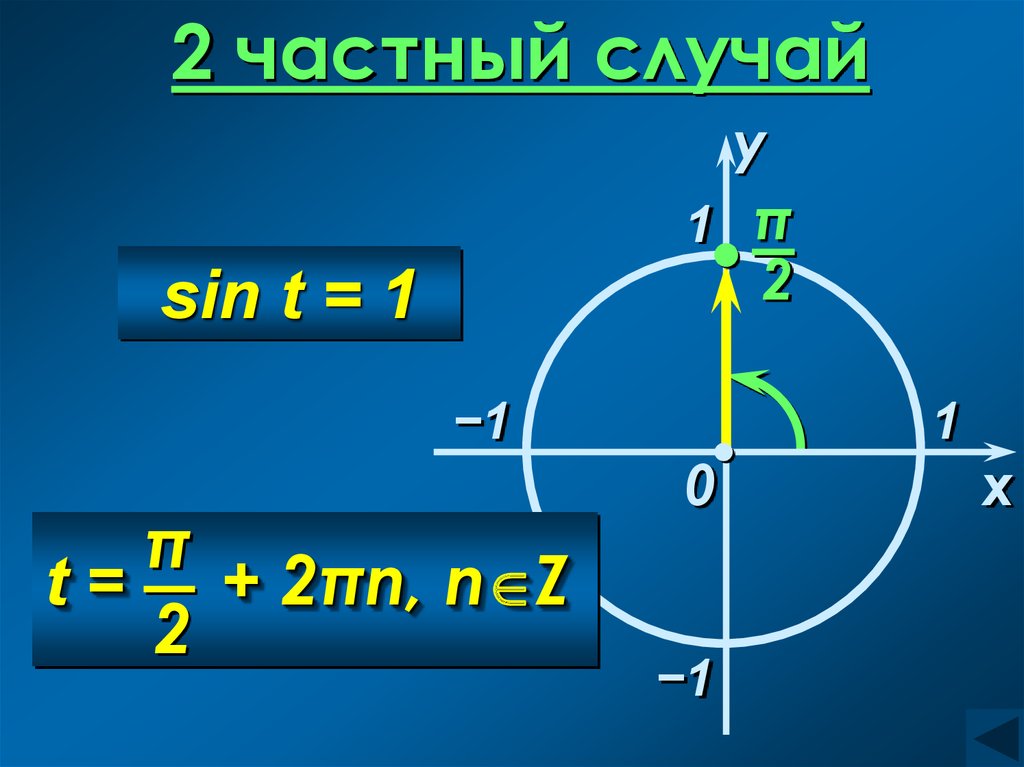
8.
2 частный случайy
1 π
2
sin t = 1
−1
π
t = + 2πn, n Z
2
0
−1
1
x
9.
3 частный случайy
1
sin t = − 1
−1
0
π
t = − + 2πn, n Z
−1 2
−1
π
−
2 −1
1
x
10. Определение арккосинуса
Арккосинусом числа а называетсятакой угол из промежутка [ 0; π],
косинус которого равен а, где lаl ≤ 1.
arccos a = t , cos t = a
где t [ 0; π]
а [− 1; 1]
arccos(- a) = п-arccosa, a [-1; 1]
11. Уравнение cos t = а
у1
arccos a
t
−1
0
−t
а
1 x
− arccos a
−1
12.
Уравнениеcos t = а
C учетом периодичности:
t = arccos a + 2πn, n Z
t = − arccos a + 2πn, n Z
Объединив в одну формулу:
t=+
arccos
a
+
2πn,
n Z
−
Пример
13.
1 частный случайy
π 1
2
cos t = 0
x
−1
0
π
−
2 −1
1
π
t = + πn, n Z
2
14.
2 частный случайy
cos t = 1
−1
1
0
t = 2πn, n Z
−1
0
1
x
15.
3 частный случайy
1
π
−1
cos t = − 1
x
0
1
t = π + 2πn, n Z
−1
16. Определение арктангенса
Арктангенсом числа а называетсятакой угол из промежутка (− 0,5π; 0,5π),
тангенс которого равен а.
arctg a = t , tg t = a
где t (− 0,5π; 0,5π)
arctg (−a) = − arctg a
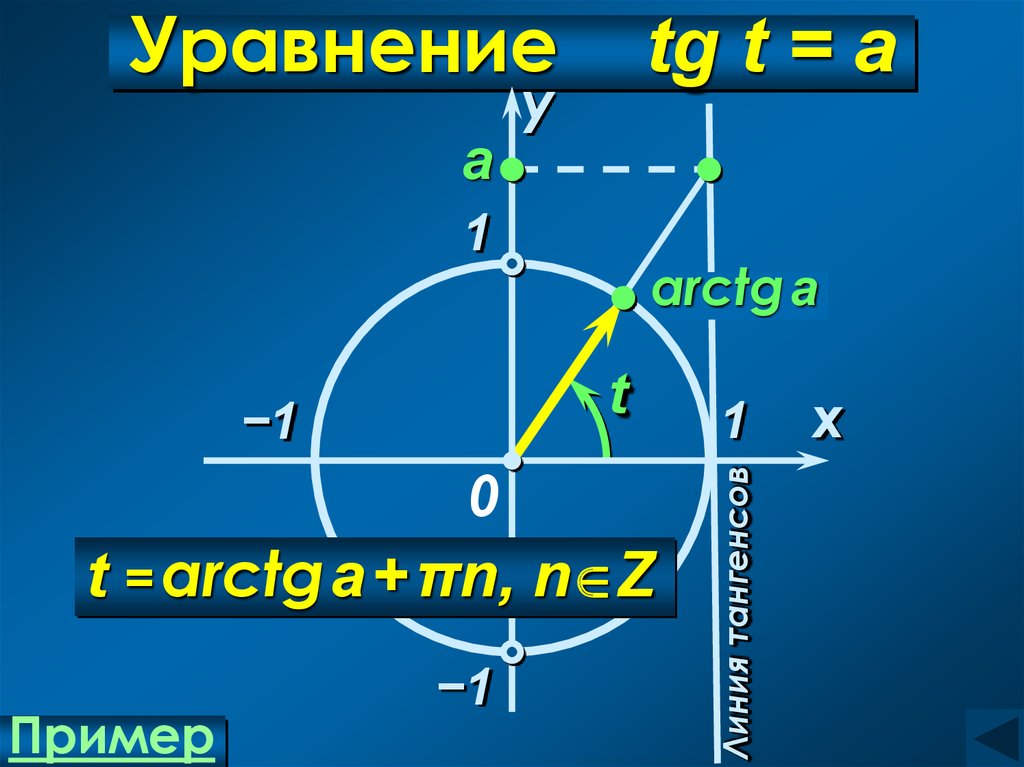
17. Уравнение tg t = а
Уравнениеу
1
arctg a
t
−1
0
t = arctga + πn, n Z
Пример
−1
1
Линия тангенсов
а
tg t = а
x
18. Определение арккотангенса
Арккотангенсом числа а называетсятакой угол из промежутка (0; π),
котангенс которого равен а.
arcсtg a = t , сtg t = a
где t (0; π)
arсctg (−a) = π − arcсtg a
19. Уравнение сtg t = а
у1
Линия котангенсов
arcсtg a
−1
t
0
x
1
а
t = arcсtg a + πn, n Z
Пример
−1
20. Примеры
Пример 3.√3
sin x = −
2
1
cos x =
2
tg x = − 1
Пример 4.
ctg x = √3
Пример 1.
Пример 2.
21.
√3Пример 1 sin t = 2
√3
t=
arcsin
+ πn, n Z
2
π
n
t = (−1)
+ πn, n Z
3
π
n
Ответ: (−1)
+ πn, n Z
3
(−1)n
22.
1Пример 2 cos x =
2
x =+
−
x=+
−
1
arccos 2 + 2πn, n Z
π
+ 2πn, n Z
3
Ответ:
π
+ + 2πn, n Z
−3
23. Пример tg x = − 1
x = arctg (− 1) + πn, n Zπ
x = − + πn, n Z
4
π
Ответ: − 4 + πn, n Z
24. Пример сtg x =
√3x = arсctg √3 + πn, n Z
π
x = + πn, n Z
6
Ответ:
π
+
πn,
n Z
6
25. Простейшие тригонометрические неравенства
Неравенство sin x ≥ aНеравенство cos x < a
Неравенство tg x > a
Неравенство ctg x ≤ a
Примеры
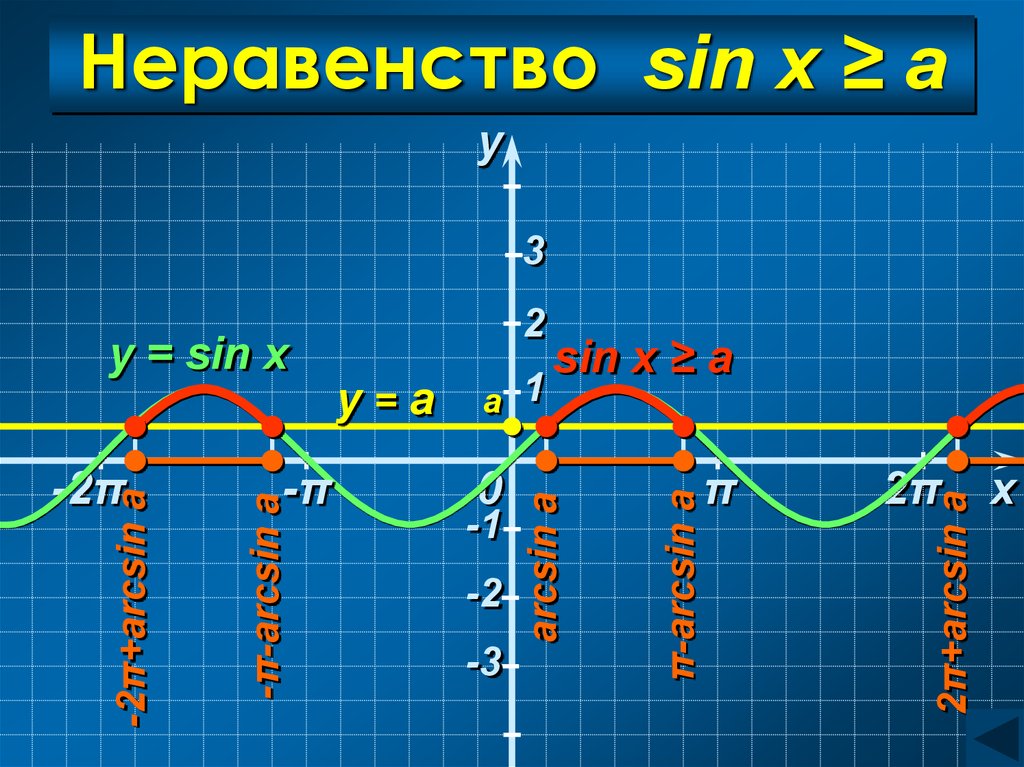
26. Неравенство sin x ≥ a
y3
0
-1
-2
-3
π
2π
2π+arcsin a
a 1
π-arcsin a
-π
-π-arcsin a
-2π+arcsin a
-2π
y=а
sin x ≥ a
arcsin a
y = sin x
2
x
27.
Неравенство sin x ≥ aarcsin a ≤ x ≤ π − arcsin a
C учетом периодичности:
arcsin a + 2πn ≤ x ≤ π − arcsin a +
+ 2πn, n Z
Ответ:
[arcsin a + 2πn; π − arcsin a + 2πn], n Z
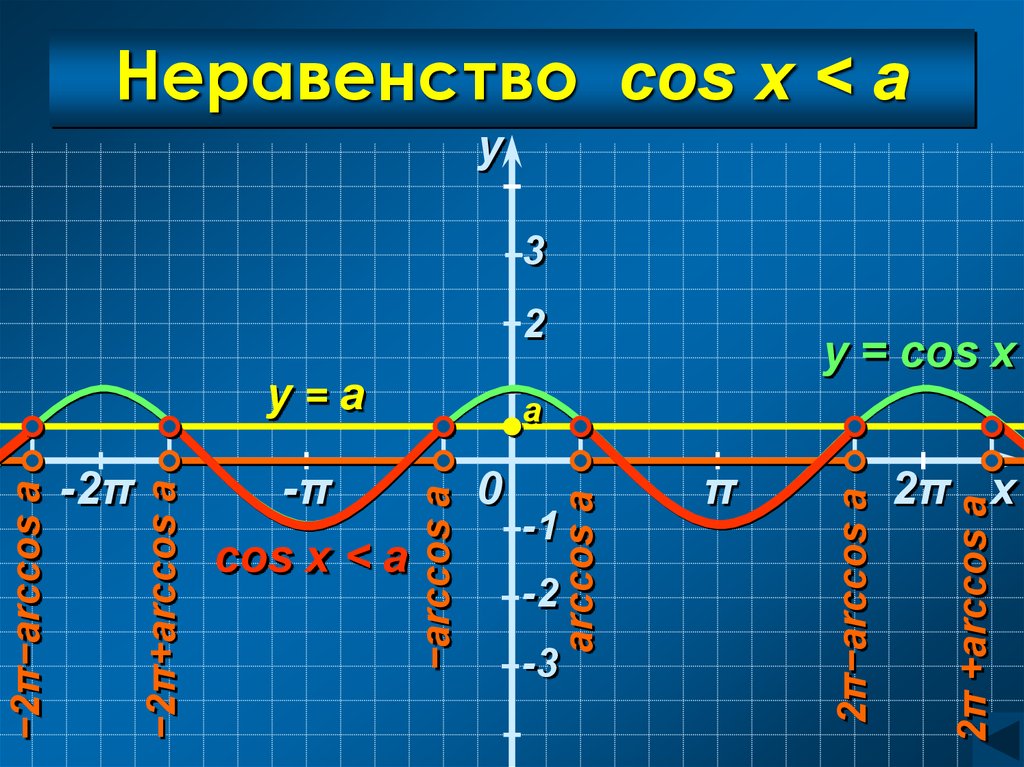
28. Неравенство cos x < a
−2π−arccos a-2π
−2π+arccos a
-π
cos x < a
−arccos a
0
-1
-2
-3
π
2π x
2π +arccos a
2
2π−arccos a
y=а
arccos a
Неравенство cos x < a
y
3
y = cos x
a
29.
Неравенство cos x < aarccos a < x < 2π − arccos a
C учетом периодичности:
arccos a + 2πn < x < 2π − arccos a +
+ 2πn, n Z
Ответ:
(arccos a + 2πn; 2π − arccos a + 2πn), n Z
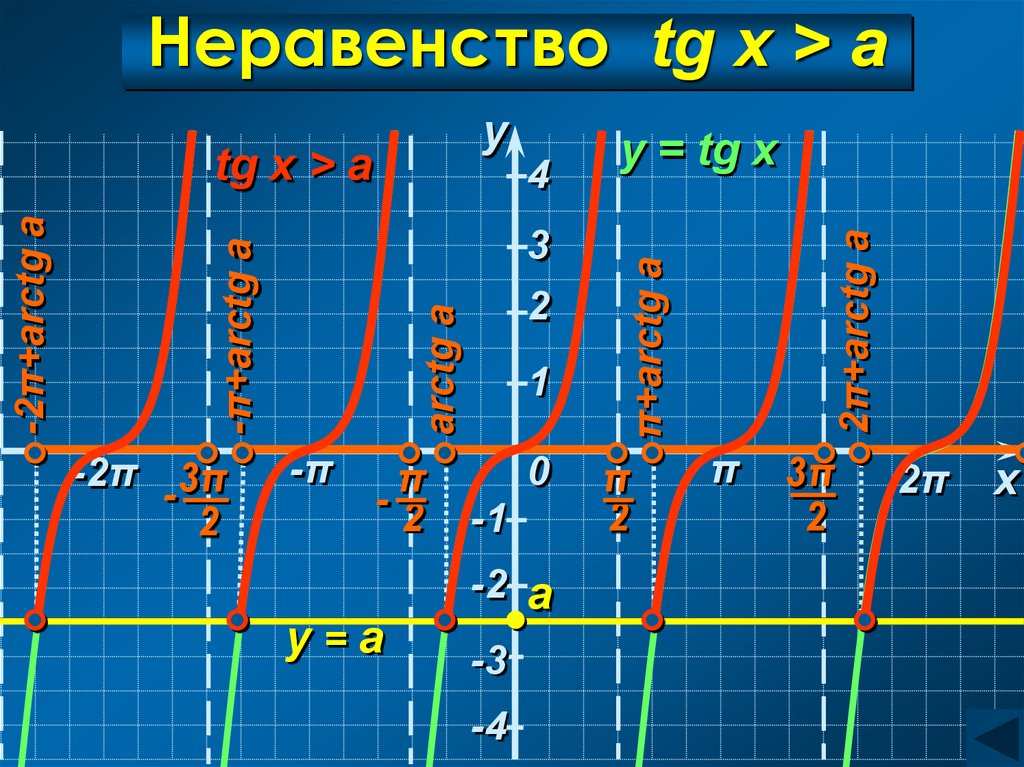
30. Неравенство tg x > a
Неравенство tg x > a3
-2π
- 3π
2
arctg a
2
-π
π
-2
y=а
1
0
-1
-2 a
-3
-4
y = tg x
2π+arctg a
4
-π+arctg a
-2π+arctg a
tg x > a
π+arctg a
y
π
2
π
3π
2
2π
x
31.
Неравенство tg x > aπ
arctg a < x <
2
C учетом периодичности:
π
arctg a + πn < x < 2 + πn, n Z
Ответ:
π
(arctg a + πn;
+ πn), n Z
2
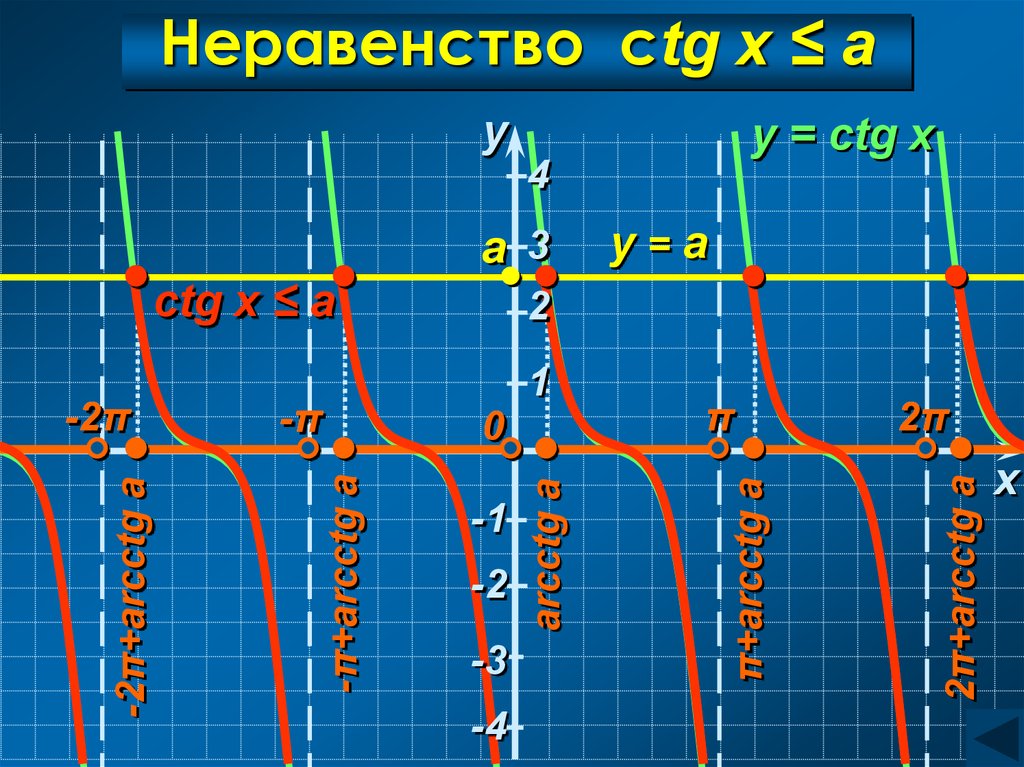
32. Неравенство ctg x ≤ a
yy = ctg x
4
a 3
ctg x ≤ a
2
-1
-2
-3
-4
arcctg a
0
π
2π
2π+arcctg a
-π
π+arcctg a
1
-π+arcctg a
-2π+arcctg a
-2π
y=а
x
33.
Неравенство ctg x ≤ aarcctg a ≤ x < π
C учетом периодичности:
arcctg a + πn < x < π + πn, n Z
Ответ:
[arctg a + πn; π+ πn), n Z
34. Примеры
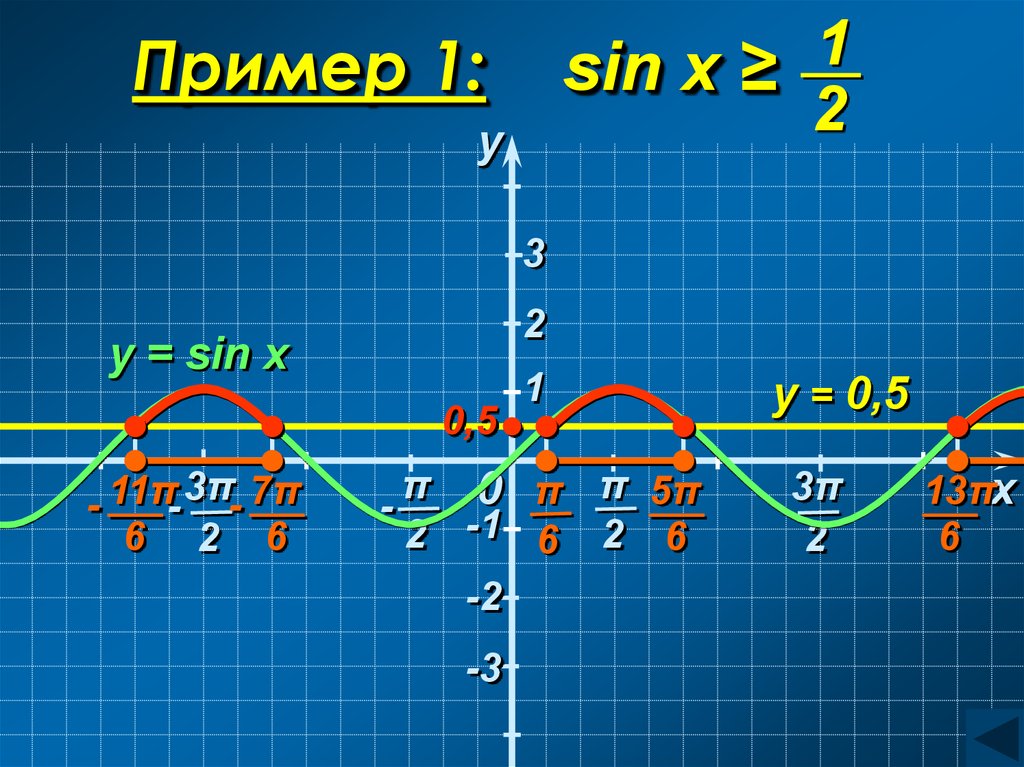
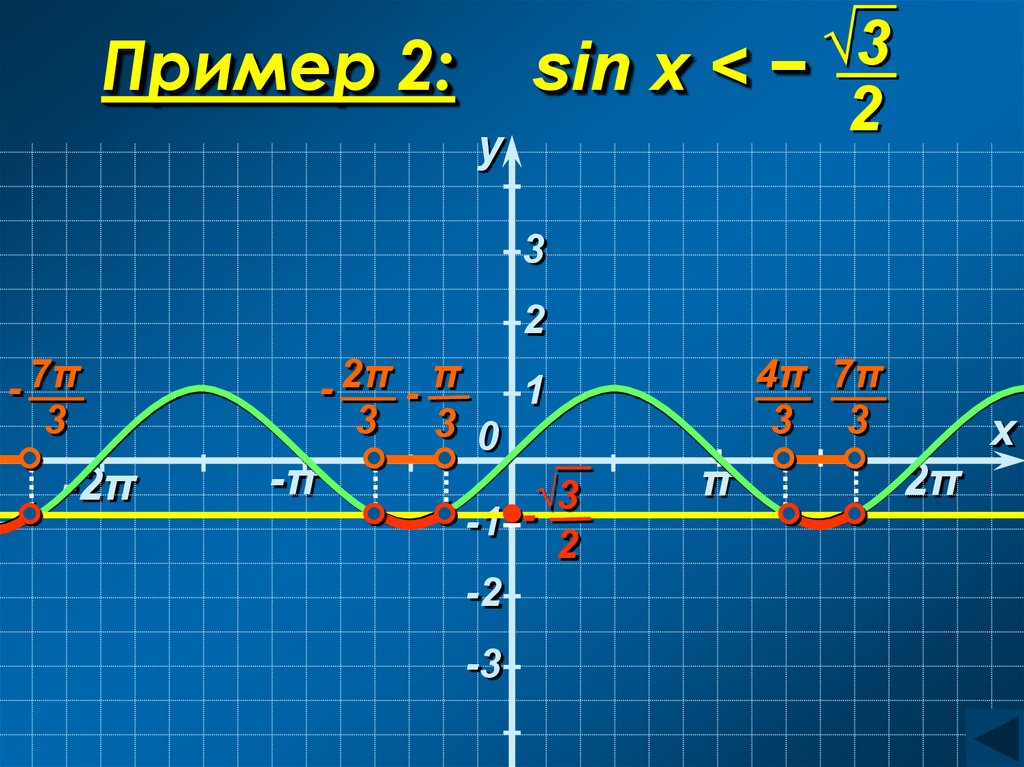
Пример 1.Пример 2.
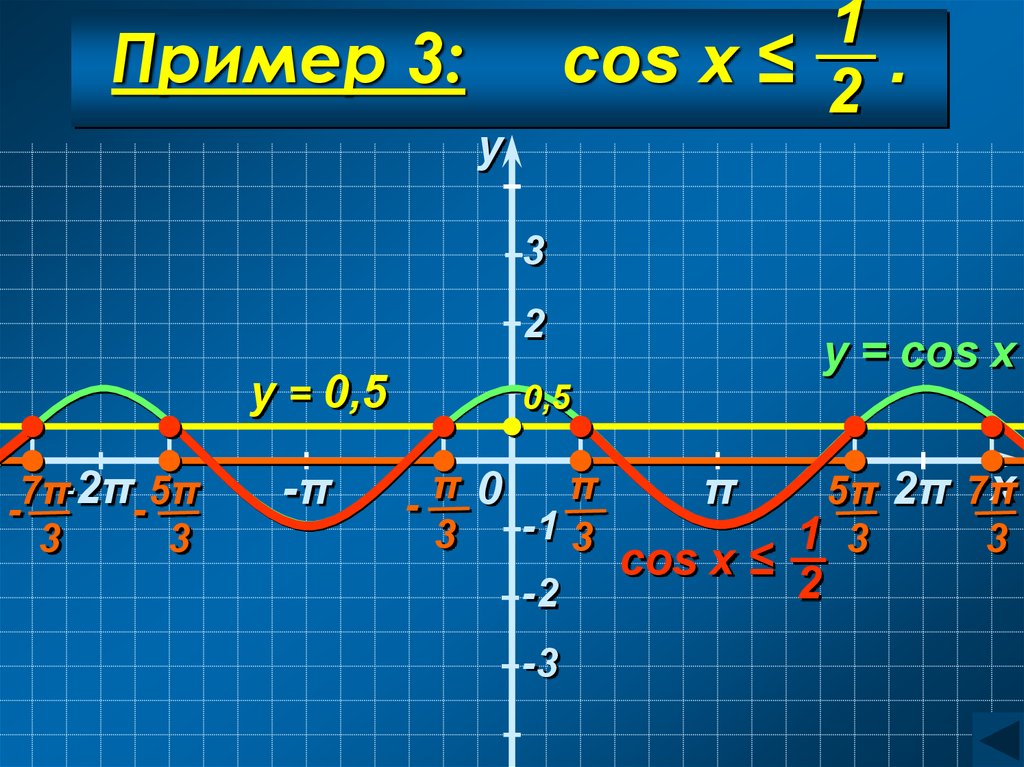
Пример 3.
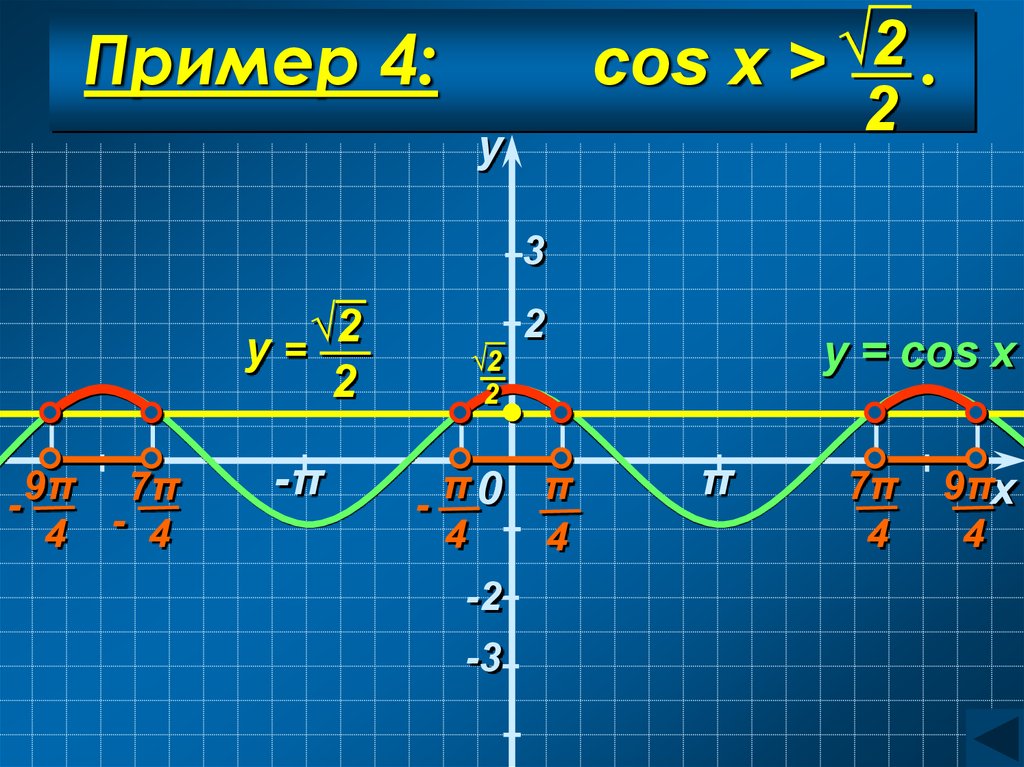
Пример 4.
1
sin x ≥
2
√3
sin x < −
2
1
cos x ≤
2
√2
cos x >
2
35.
1sin x ≥
2
Пример 1:
y
3
2
y = sin x
0,5
3π
11π
- - 7π
6 2 6
1
π 0 π π 5π
2 -1 6 2 6
-2
-3
y = 0,5
3π
2
13πx
6
36.
1Пример 1: sin x ≥ .
2
π
5π
≤
x
≤
6
6
C учетом периодичности:
π
5π
+ 2πn ≤ x ≤
+ 2πn, n Z
6
6
Ответ:
5π
π
+ 2πn; 6 + 2πn , n Z
6
37. Пример 2: sin x < −
Пример 2:y
√3
sin x < −
2
3
2
- 7π
3
-2π
- 2π - π
1
3 3 0
-π
√3
-1
2
-2
-3
4π 7π
3 3
π
x
2π
38.
√3Пример 2: sin x < − .
2
π
2π
−
<x<−
3
3
C учетом периодичности:
π
2π
− 3 + 2πn < x < − 3 + 2πn, n Z
Ответ:
π
2π
− + 2πn; − + 2πn , n Z
3
3
39. Пример 3: cos x ≤ .
1cos x ≤ 2 .
Пример 3:
y
3
2
y = 0,5
-7π-2π- 5π
3
3
-π
y = cos x
0,5
π
π
x
0
π
2π
5π
7π
-1 3
3
1 3
3
cos x ≤
2
-2
-3
40.
1Пример 3: cos x ≤ 2 .
π
5π
≤
x
≤
3
3
C учетом периодичности:
π
5π
+
2πn
≤
x
≤
+
2πn,
n Z
3
3
Ответ:
5π
π
+ 2πn; 3 + 2πn , n Z
3
41. Пример 4: cos x > .
√2cos x > .
2
Пример 4:
y
3
√2
y=
2
9π
7π
4 - 4
-π
√2
2
π
- 0
4
-2
-3
2
π
4
y = cos x
π
7π
4
9πx
4
42.
√2Пример 4: cos x >
.
2
π
π
− 4 <x< 4
C учетом периодичности:
π
π
− + 2πn < x <
+ 2πn, n Z
4
4
Ответ:
π
π
− + 2πn;
+ 2πn , n Z
4
4






























 Математика
Математика








