Похожие презентации:
Тригонометрические уравнения
1.
2. Тригонометрические уравнения
http://aida.ucoz.ru3. Девиз : « Не делай никогда того, чего не знаешь , но научись всему, что следует знать» Пифагор
4. С помощью тригонометрической окружности найти все значения из промежутка [-2π; 2π] для следующих выражений
arcsin 0,arcsin
5. Верно ли равенство
1а ) arccos ;
2 3
3 11
г ) arcsin
;
2
6
2
б ) arcsin(
) ;
2
4
2
3
д) arccos(
)
.
2
4
3
в ) arccos(
) ;
2
6
е)arctg 3
3
.
6. Имеет ли смысл выражение:
7. Определение.
•Уравнения вида f(x) = а, где а – данноечисло, а f(x) – одна из тригонометрических
функций,
называются
простейшими
тригонометрическими уравнениями.
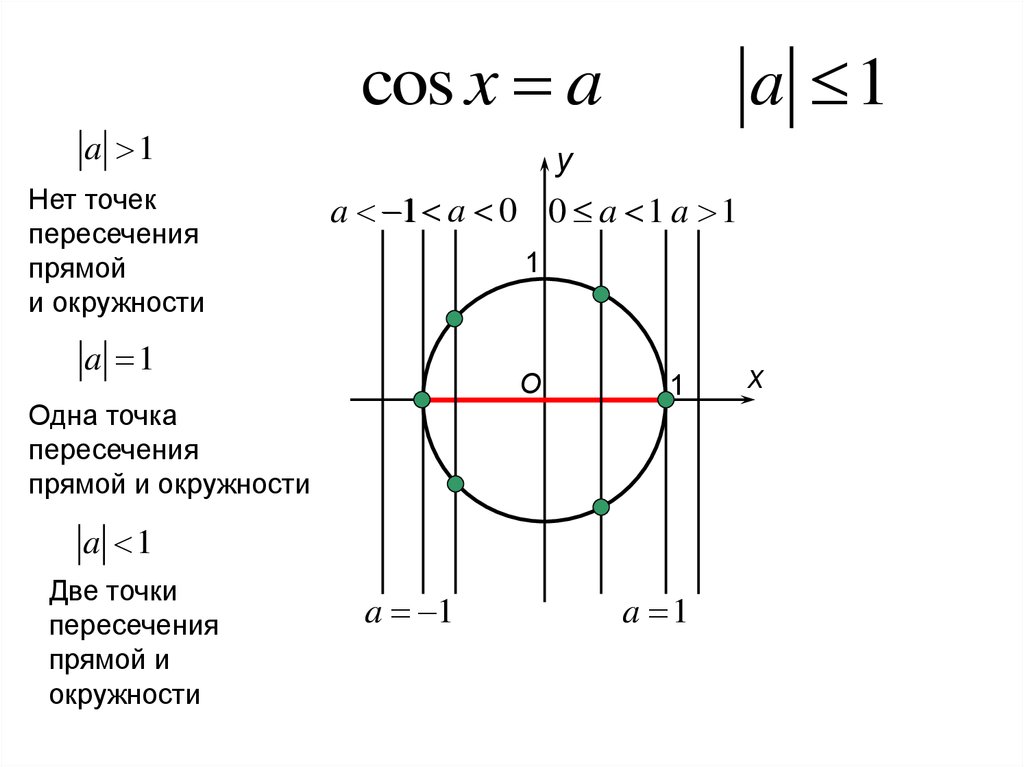
8. Решение уравнения cos x = a
9.
cos x aa 1
Нет точек
пересечения
прямой
и окружности
a 1
y
a 1 a 0 0 a 1 a 1
1
a 1
O
Одна точка
пересечения
прямой и окружности
1
a 1
Две точки
пересечения
прямой и
окружности
a 1
a 1
x
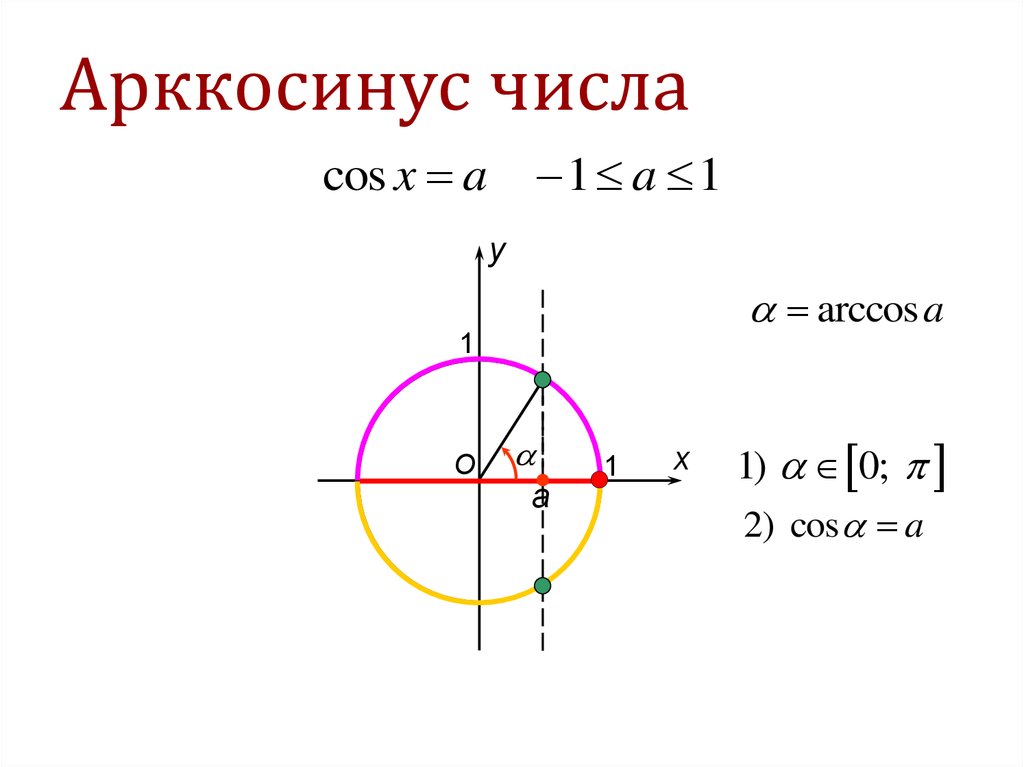
10. Арккосинус числа
cos x a1 a 1
y
arccosa
1
O
a
1
x
1) 0;
2) cos a
11. Решение уравнения
cos x ay
1
arccosa
a 1
x
O
arccosa
x arccos a 2 n, n
x arccos a 2 n, n
x arccos a 2 n, n
12. Уравнение cos t = a
•в) при x = -1 имеет одну сериюyрешений
1
x = π + 2πn, n ϵ Z ;
-1
a 1
O
x
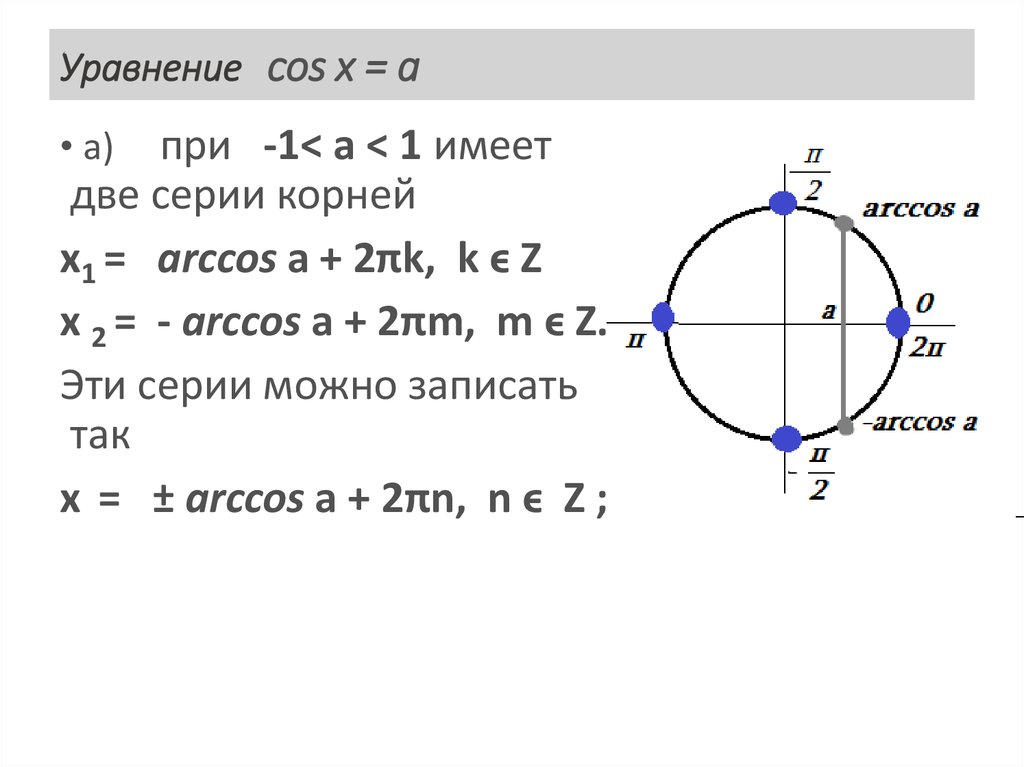
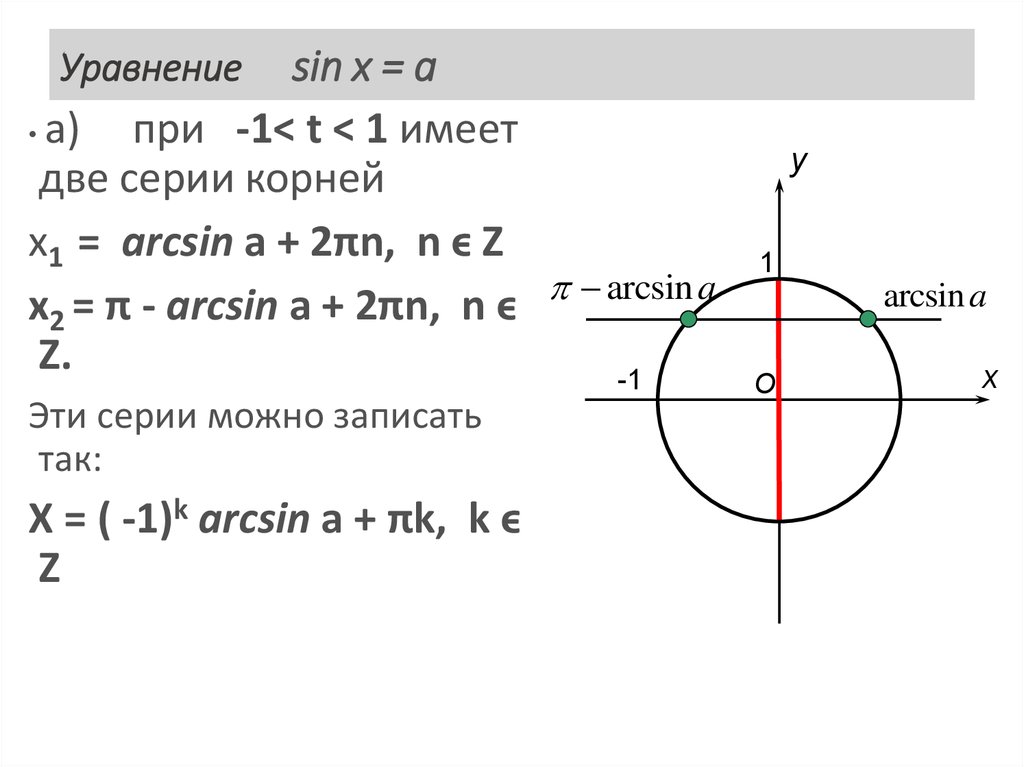
13. Уравнение cos x = a
• a)при -1< a < 1 имеет
две серии корней
x1 = arсcos a + 2πk, k ϵ Z
x 2 = - arсcos a + 2πm, m ϵ Z.
Эти серии можно записать
так
x = ± arсcos a + 2πn, n ϵ Z ;
14. Уравнение cos x = a
•б) при а = 1 имеет одну сериюyрешений
1
x = 2πn, n ϵ Z ;
O
1
a 1
x
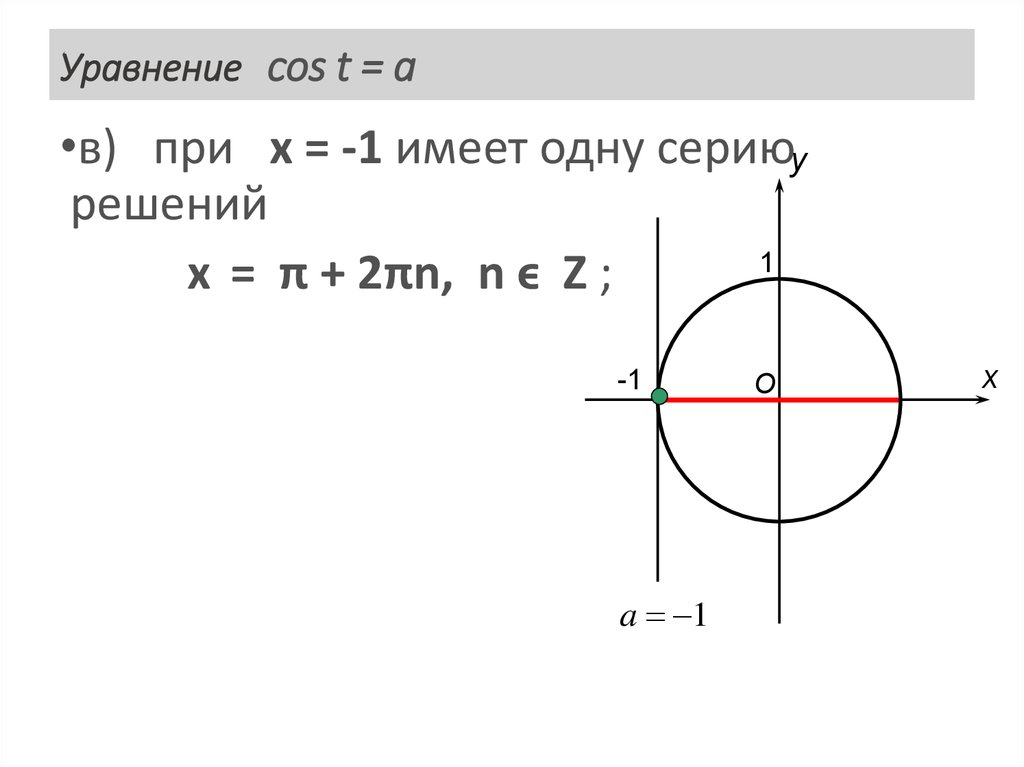
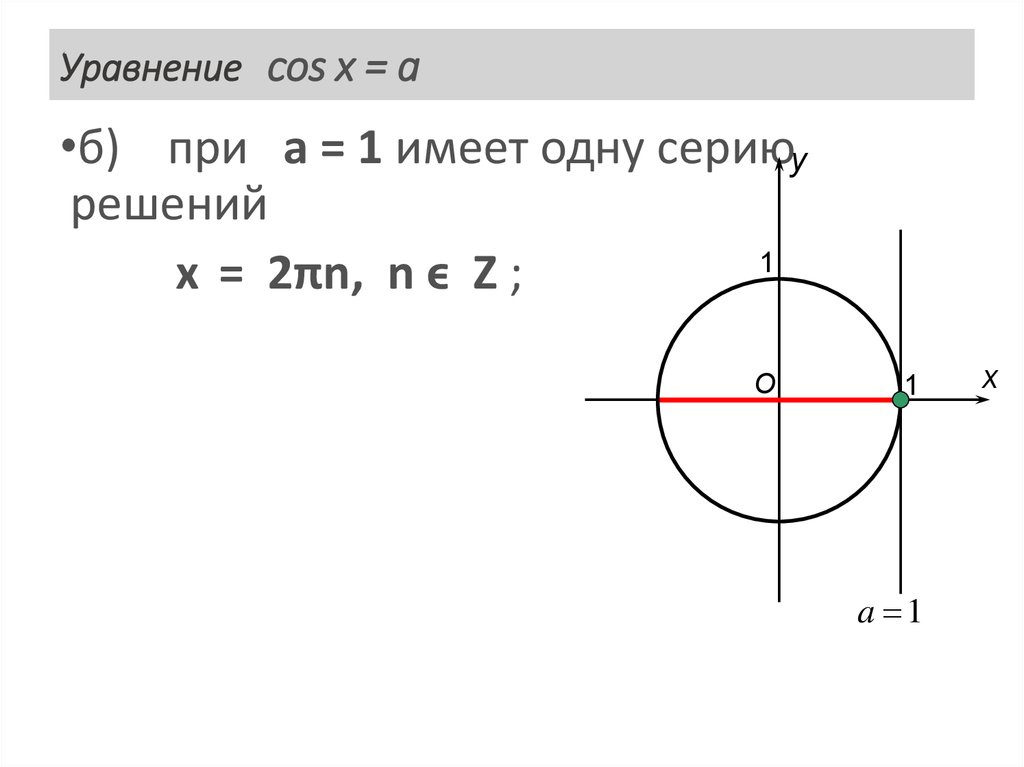
15. Уравнение cos x = a
•в) при а = -1 имеет одну сериюyрешений
1
x = π + 2πn, n ϵ Z ;
-1
a 1
O
x
16. Уравнение cos x = a
y1
-1
O
x
17. Уравнение cos x = a
д) при а > 1 и a < -1уравнение не имеет
корней.
y
1
-1
O
1
x
18. Решите уравнение
1)1
cos х =2
2) cos х =
1
-2
19. Решите уравнение
3) cos 4x = 14x = 2πn, n ϵ
Z
4)
20. Решите уравнение
.Решите уравнение
5)
21. Решите уравнение и укажите корни, принадлежащие промежутку [-π;-2π].
Решите уравнениепринадлежащие
а)
и укажите корни,
промежутку [-π;-2π].
22. б) сделаем выборку корней, принадлежащих промежутку [-2π; -π].
1) с помощью окружности4
2) с помощью графика
2
A
-10
-5
5
-2
Ответ : а)
б)
-4
1
23. Задание 1. Найти корни уравнения:
1) a) cos x =1 б) cos x = - 1 в) cos x = 0г) cos x =1,2
д) cos x = 0,2
2) а)
б)
в)
г)
24.
y asin x a
a 1
Нет точек
пересечения
прямой
и окружности
a 1
Одна точка
пересечения
прямой и окружности
a 1
Две точки
пересечения прямой
и окружности
a 1
y
1
O
1
y a
y a
y a
a 1
a 1
0 a 1
y a
1 a 0
a 1
a 1
x
y a
y a
25. Арксинус числа
sin x ay
1
1 a 1
2
arcsin a
a
O
2
1
x
1) ;
2 2
2) sin a
26. Решение уравнения
sin x ay
arcsin a
1
a
arcsin a
1
x
O
x arcsin a 2 k , k
x arcsin a 2 k , k
x arcsin a 2k 1 , k
x arcsin a 2k , k
x 1 arcsin a n, n
n
27. Уравнение sin x = a
sin x = a• a)
при -1< t < 1 имеет
две серии корней
x1 = arсsin a + 2πn, n ϵ Z
arcsin a
x2 = π - arсsin a + 2πn, n ϵ
Z.
-1
Уравнение
Эти серии можно записать
так:
X = ( -1)k arсsin a + πk, k ϵ
Z
y
1
arcsin a
O
x
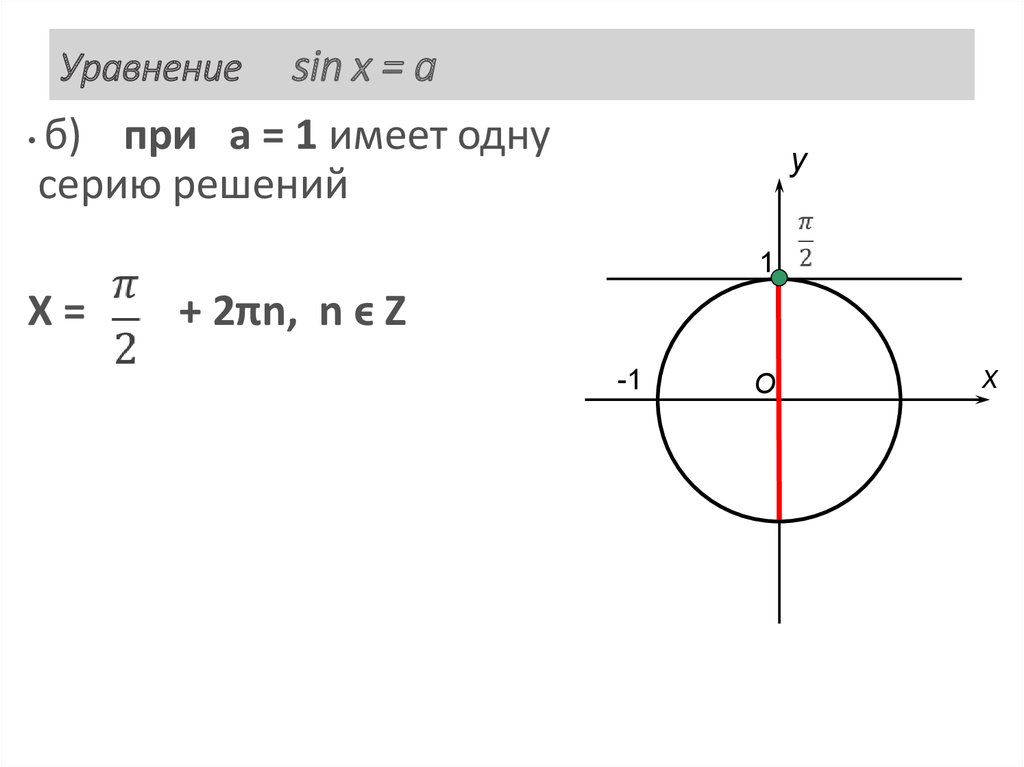
28. Уравнение sin x = a
sin x = a• б)
при а = 1 имеет одну
серию решений
Уравнение
y
1
X=
+ 2πn, n ϵ Z
-1
O
x
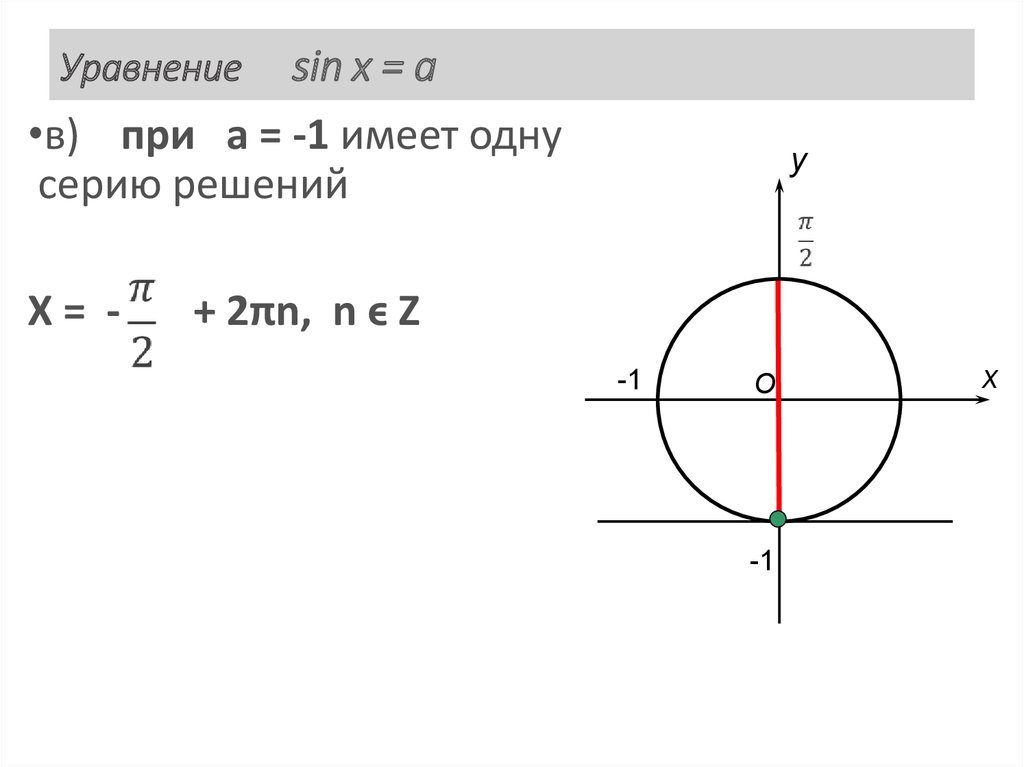
29. Уравнение sin x = a
sin x = a•в) при а = -1 имеет одну
серию решений
Уравнение
X= -
y
+ 2πn, n ϵ Z
-1
O
-1
x
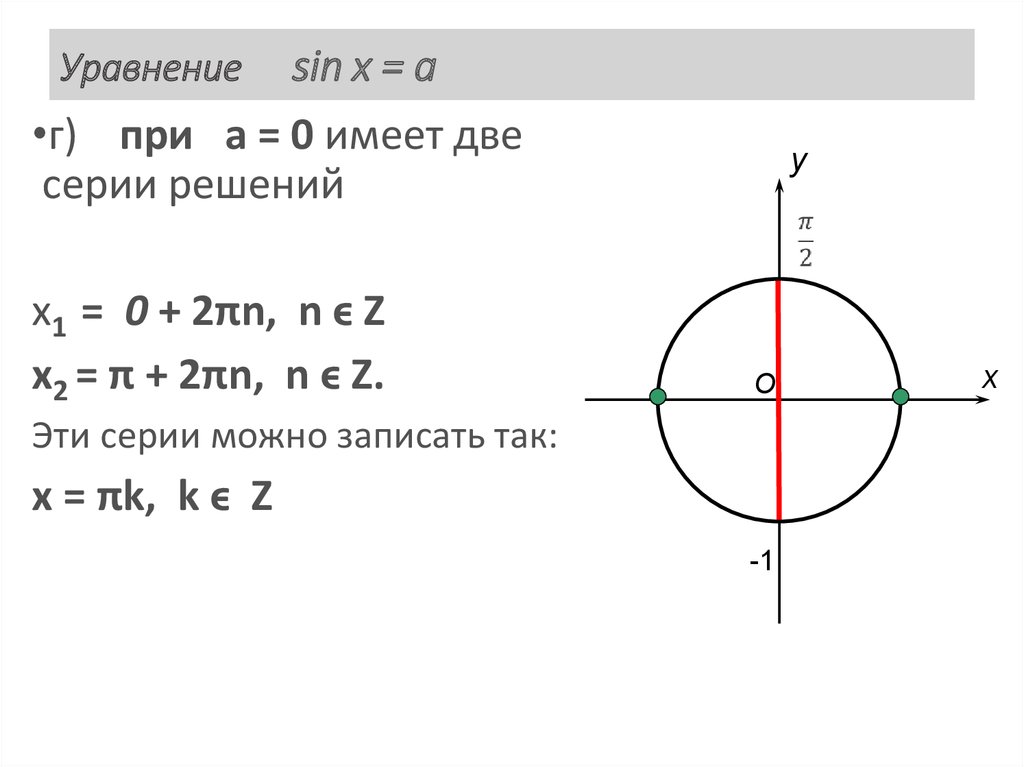
30. Уравнение sin x = a
sin x = a•г) при а = 0 имеет две
серии решений
Уравнение
x1 = 0 + 2πn, n ϵ Z
x2 = π + 2πn, n ϵ Z.
y
O
Эти серии можно записать так:
x = πk, k ϵ Z
-1
x
31. Решите уравнение
,,Решите уравнение
1) sin х =
x = ( -1)k
+ πk,
kϵ Z.
32. Решите уравнение
(;,,;
Решите
уравнение
2) sin х = - 2
2
x = ( -1)k ( -
+ πk, k ϵ Z
33. Задание 2. Найти корни уравнения:
Задание 2. Найти корни уравнения:1) a) sin x =1 б) sin x = - 1 в) sin x = 0
г) sin x =1,2
2) а)
в)
д) sin x = 0,7
б)
г)
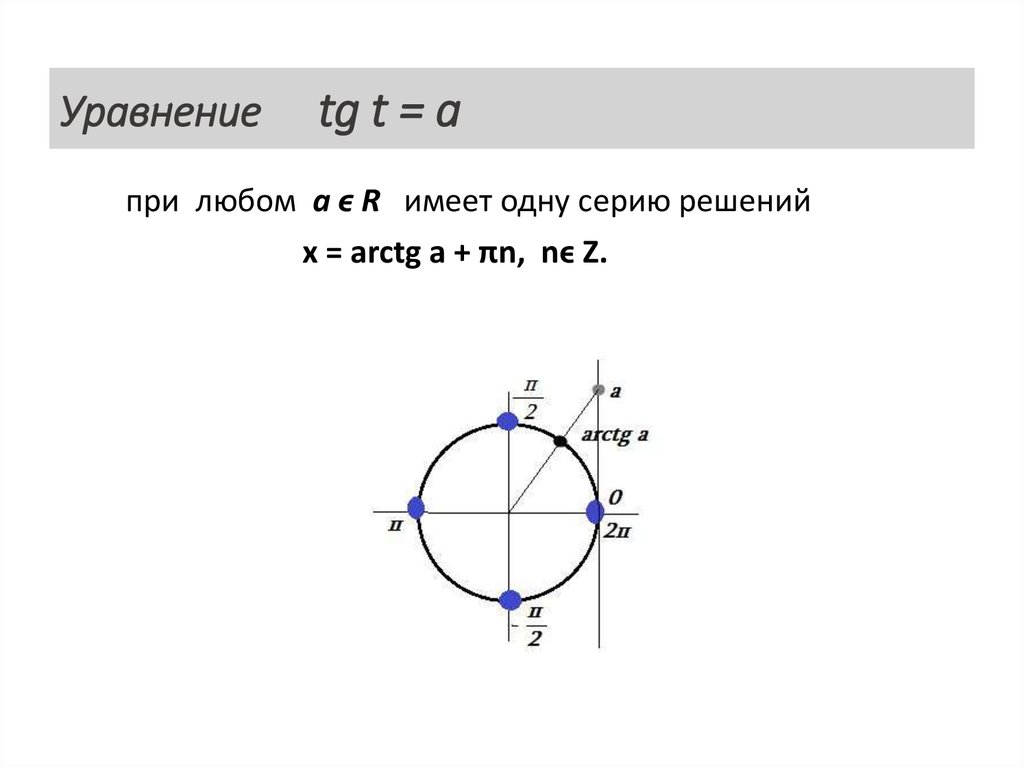
34. Уравнение tg t = a
при любом а ϵ R имеет одну серию решенийх = аrctg a + πn, nϵ Z.
35. Решите уравнение
2) x= tg (-1) x= tg
х = аrctg
+ πn, nϵ
x=
х = аrctg(x=-
Z.
+ πn, nϵ Z.
)
) + πn, nϵ Z,
+ πn, nϵ Z.
36. Уравнение ctg t = a
при любом а ϵ R имеет одну серию решенийх = аrcctg a + πn, nϵ Z.
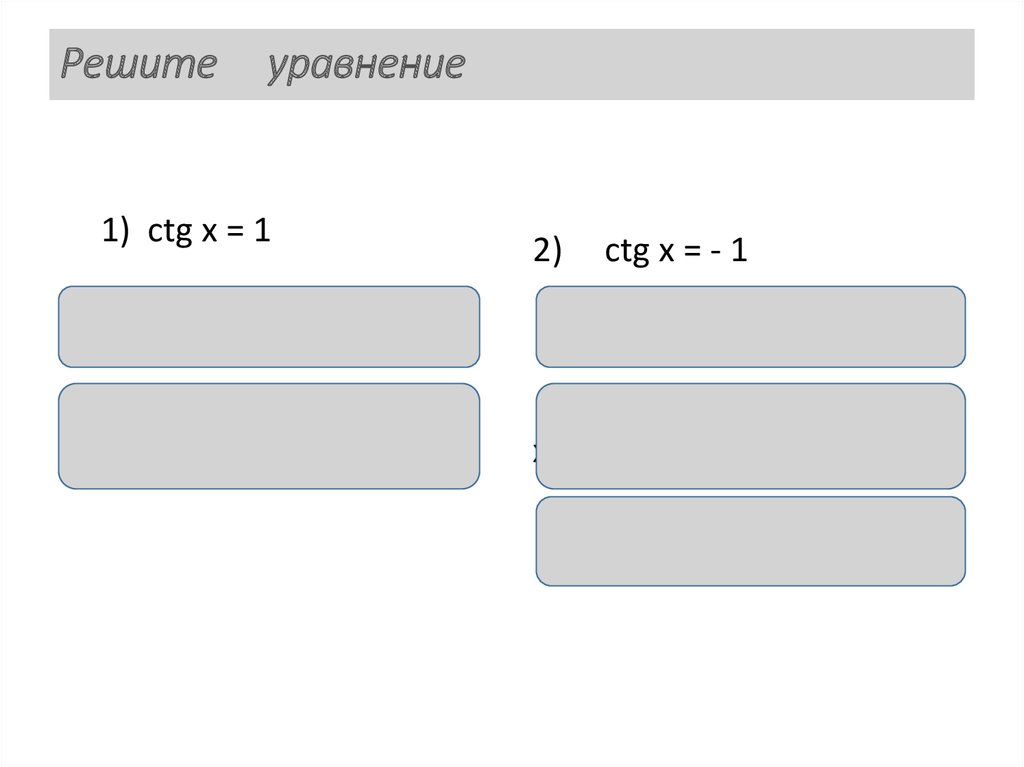
37. Решите уравнение
1) ctg x = 12)
ctg x = - 1
х = аrcctg 1 + πn, nϵ Z,
х = аrcctg ( -1) + πn, nϵ Z
х=
х = π - аrcctg 1 + πn, nϵ Z
+ πn, nϵ Z.
х=
+ πn, nϵ Z.



![С помощью тригонометрической окружности найти все значения из промежутка [-2π; 2π] для следующих выражений С помощью тригонометрической окружности найти все значения из промежутка [-2π; 2π] для следующих выражений](https://cf2.ppt-online.org/files2/slide/m/MKSJHVnfvqW6aZPylmpIUcgeChd4Nwu0FtzxrLXOTG/slide-3.jpg)











![Решите уравнение и укажите корни, принадлежащие промежутку [-π;-2π]. Решите уравнение и укажите корни, принадлежащие промежутку [-π;-2π].](https://cf2.ppt-online.org/files2/slide/m/MKSJHVnfvqW6aZPylmpIUcgeChd4Nwu0FtzxrLXOTG/slide-20.jpg)
![б) сделаем выборку корней, принадлежащих промежутку [-2π; -π]. б) сделаем выборку корней, принадлежащих промежутку [-2π; -π].](https://cf2.ppt-online.org/files2/slide/m/MKSJHVnfvqW6aZPylmpIUcgeChd4Nwu0FtzxrLXOTG/slide-21.jpg)









 Математика
Математика








