Система автоматического регулирования возбуждения генератора (САР)

1. ИССЛЕДОВАНИЕ САР ВОЗБУЖДЕНИЯ ГЕНЕРАТОРА

2.

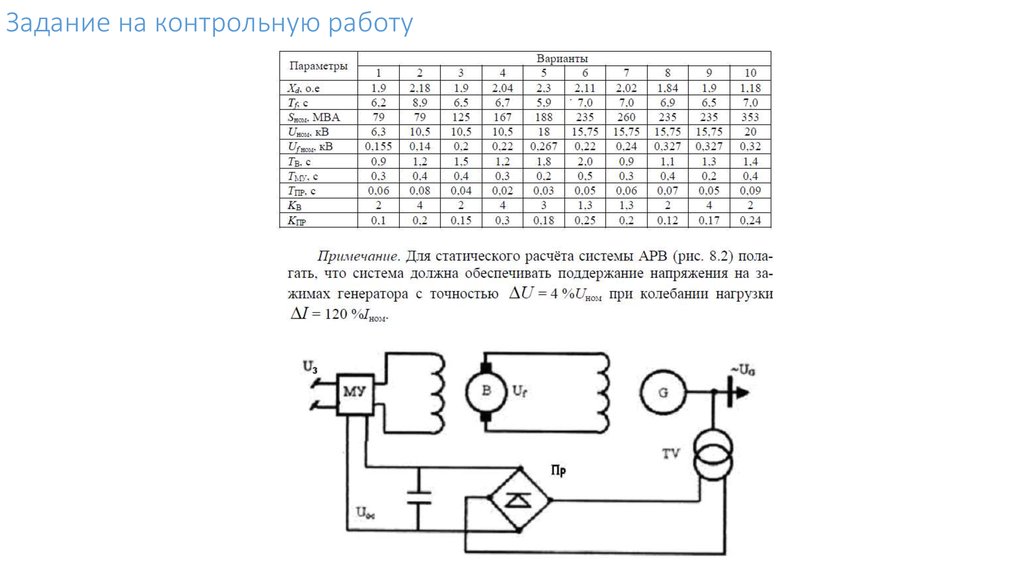
Задание на контрольную работу

3.

1. Статический расчет системы
Целью статического расчета замкнутой системы является определение коэффициентов усиления системы или одного
из ее элементов из условия точности поддержания выходного сигнала (напряжения генератора) при заданной
величине возмущающего воздействия (колебания тока нагрузки) или при заданной зоне нечувствительности
астатического элемента.
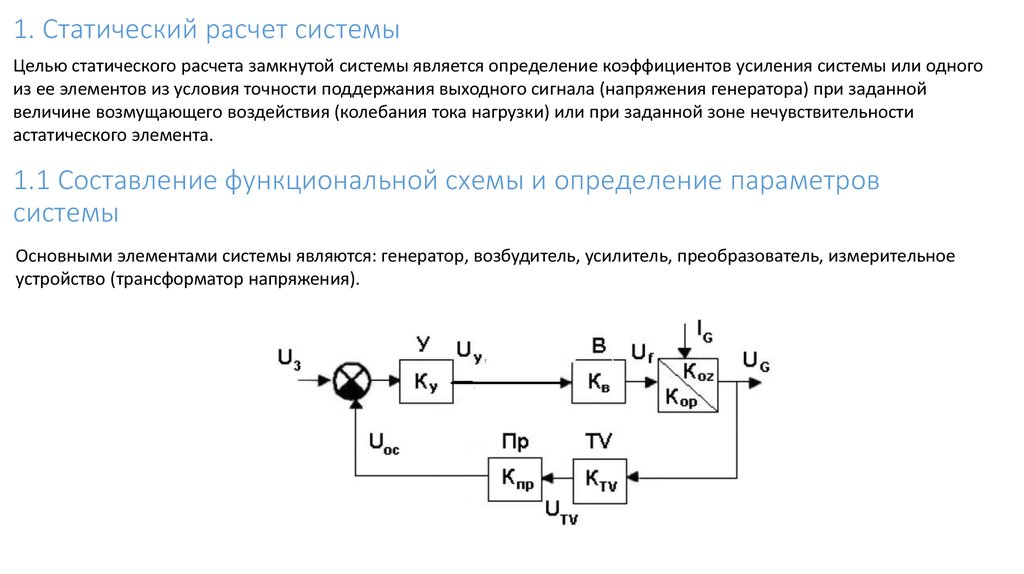
1.1 Составление функциональной схемы и определение параметров
системы
Основными элементами системы являются: генератор, возбудитель, усилитель, преобразователь, измерительное
устройство (трансформатор напряжения).

4.

Каждый элемент схемы является преобразователем информации, поступающей на вход. Количественное
соотношение входного и выходного сигналов оценивается передаточным коэффициентом К.
При наличии нескольких входных сигналов элемент описывается уравнением с несколькими передаточными
коэффициентами. Например, генератор, являющийся объектом регулирования в системе, имеет два входных сигнала
– управляющее воздействие Uf и возмущающее воздействие IG

5.

Передаточные коэффициенты генератора как объекта регулирования определяют следующим образом:
где ЕGном – номинальная ЭДС генератора, кВ
Приближенно её можно определить как
где Xd – внутреннее сопротивление генератора, Ом (полная синхронная реактивность по продольной оси),
IGном– номинальный ток генератора, кА.
Если сопротивление в исходных данных выражено в относительных единицах, то необходимо перевести его в Омы
по формуле
где SGном – номинальная мощность генератора, МВА.

6.

Далее определяем коэффициент объекта по возмущению, Ом:
Для трансформатора напряжения, стандартное напряжение которого на выходе – 0.1 кВ, передаточный коэффициент
определяется по формуле

7.

1.2 Описание системы в установившемся режиме
Система описывается функциональной схемой или уравнениями:
Осуществляя взаимоподстановку, исключая промежуточные переменные, а также применяя искусственный
прием умножения и деления слагаемого, содержащее U, на коэффициенты обратной связи и полагая, что
получим уравнение статической ошибки:

8.

При настройке стабилизирующей системы на номинальное значение напряжение генератора при номинальном токе
выражение для ошибки примет вид:
где Кр.с. – коэффициент передачи разомкнутой системы, т.е. произведение всех коэффициентов передачи по основному
контуру
Из выражения статической ошибки можно определить любой недостающий параметр, например, коэффициент Ky:
Где ∆IG=120%*IG ном ; ∆UG=4%*UG ном

9.

На основании приведенных выражений осуществляется построение статических характеристик (зависимости Ug от Ig)
системы АРВ для замкнутой и разомкнутой системы (когда Ктv * Кпр = 0)

10.

2. Анализ устойчивости системы
2.1 Математическое описание системы в динамическом режиме
Исследование устойчивости системы проводится по нескольким критериям на основе функциональной схемы в
динамическом режиме. При таком описании схемы следует иметь в виду, что к апериодическим звеньям первого
порядка относятся звенья, для которых заданы передаточный коэффициент К и постоянная времени Т. Звенья, для
который указан только коэффициент К считаются безынерционными. Поскольку устойчивость линейных систем
определяется параметрами самих систем и не зависит от возмущающих воздействий, то величину возмущения можно
считать равной нулю. Соответственно, структурная схема системы примет вид:

11.

Передаточная функция разомкнутой системы:
Передаточная функция замкнутой системы определяется как:
Где Wохв – передаточная функция, охватываемая обратной связью

12.

2.2 Оценка устойчивости системы АРВ
2.2.1 Оценка устойчивости по критерию Гурвица
Оценка устойчивости по критерию Гурвица осуществляется построением главного определителя Гурвица. По главной
диагонали слева направо выставляются все коэффициенты характеристического уравнения. Столбцы вверх от главной
диагонали заполняются коэффициентами с последовательно возрастающими индексами, а столбцы вниз – с
последовательно убывающими. На место коэффициентов с индексами больше n и меньше нуля ставятся нули.
Отчеркивая в главном определителе диагональные миноры, получаем определители Гурвица низшего порядка
Для того, чтобы система считалась устойчивой, необходимо и достаточно, чтобы все определители Гурвица и имели
одинаковый знак с коэффициентом а0, т.е. при а0>0 были положительными.

13.

2.2.1 Оценка устойчивости по критерию Михайлова
Оценка устойчивости по критерию Михайлова производится на основе характеристического многочлена, полученного из
знаменателя передаточной функции замкнутой системы и записанного в частотной форме:
где F(jw) – вектор Михайлова, U(w) – вещественная часть выражения, jV(w) – мнимая часть выражения.
Кривая зависимости вещественной и мнимой части, построенная в комплексной плоскости при изменении частоты w от
0 до ∞, называется годографом Михайлова. Для устойчивой системы управления n-го порядка необходимо и
достаточно, чтобы годограф Михайлова, начиная с вещественной положительной полуоси, проходил против часовой
стрелки последовательно через n – квадрантов.

14.

2.2.3 Построение области устойчивости (D-разбиения)
Область D-разбиения в пространстве одного из параметров системы, например Ку, строится на основании
характеристического многочлена передаточной функции. Коэффициент а4 этого многочлена содержит все s
коэффициентов системы, в том числе и Ку
где
- произведение остальных передаточных коэффициентов элементов разомкнутой системы
Данное выражение можно подставить в характеристическое уравнение системы в комплексной форме и выразить из
него коэффициент Ку :
На комплексной плоскости строится кривая зависимости вещественной и мнимой части при изменении частоты от -∞ до
∞.

15.

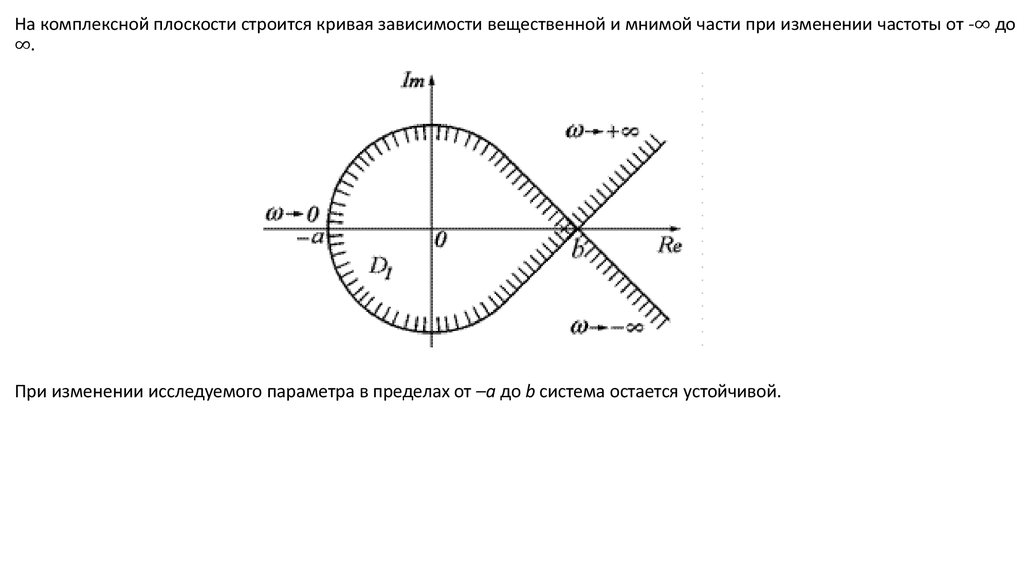
На комплексной плоскости строится кривая зависимости вещественной и мнимой части при изменении частоты от -∞ до
∞.
При изменении исследуемого параметра в пределах от –а до b система остается устойчивой.

16.

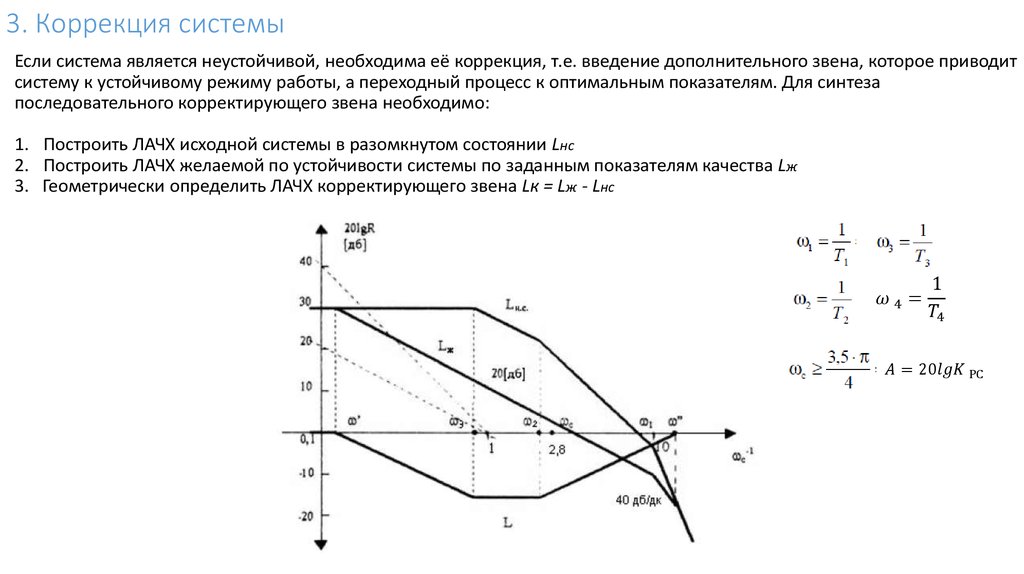
3. Коррекция системы
Если система является неустойчивой, необходима её коррекция, т.е. введение дополнительного звена, которое приводит
систему к устойчивому режиму работы, а переходный процесс к оптимальным показателям. Для синтеза
последовательного корректирующего звена необходимо:
1. Построить ЛАЧХ исходной системы в разомкнутом состоянии Lнс
2. Построить ЛАЧХ желаемой по устойчивости системы по заданным показателям качества Lж
3. Геометрически определить ЛАЧХ корректирующего звена Lк = Lж - Lнс