Понятие логарифма. Свойства логарифма. Десятичные и натуральные логарифмы

1. Понятие логарифма. Свойства логарифма. Десятичные и натуральные логарифмы.

2. Основные вопросы:

1. Понятие логарифма. Свойства
логарифма.
2. Формула перехода к другому
основанию.
3. Десятичные и натуральные
логарифмы.

3. Немного истории

Потому-то, словно пена
Опадают наши рифмы
И величие степенно
Отступает в логарифмы.
Борис Слуцкий
Первый изобретатель
логарифмов —
шотландский барон Джон
Непер (1550—1617)

4. Решите уравнение.

1)
Мы искали
х показатель степени,
Решить
а надо
в, где
а 0основание
и а 1, b0,5 ,0
0,5х =32,уравнение
в который
возвести
х = - 5.
чтобы получить 32.
значит, найти показательстепени,
2)
в который надоМы
возвести
основание
a,
искали показатель
степени,
в который надо возвести основание
чтобы получить
число b
чтобы получить 27.
1
,
3
3)
Показатель
степени – это и есть логарифм
4х+1+4х = 320 , Мы искали показатель степени,
условиях).
4х(4+1) (при
= 320 ,определенных
в который надо возвести
основание 4,
4х = 64 ,
чтобы получить 64.
х = 3.

5.

Слово ЛОГАРИФМ
происходит от греческих слов
- число и отношение
• Первые таблицы логарифмов назывались
• «Описание удивительной таблицы
логарифмов»
(1614 г.) и
• «Устройство удивительной таблицы
логарифмов»
(1619 г.)
5

6. Определение логарифма

Логарифмом числа b>0 по основанию
a>0, a ≠ 1 , называется показатель степени,
в которую надо возвести число a, чтобы
получить число b.
Логарифм числа b по основанию a
обозначается
logab

7. ПРИМЕРЫ

1) log232, здесь b = 32, a = 2, c = 5.
log232 = 5 , т. к. 25 = 32 .
2) log50,04 ,
здесь b = 0,04, a = 5, c = - 2.
log50,04 = - 2, т. к. 5-2 = 1/25 = 0,04 .
3) Найти х, такое, что log8х = 1/3.
По определению логарифма
х = 81/3 = 2.

8.

c
a
= b logab = c
Откуда получаем основное
логарифмическое тождество
(b > 0, a > 0, a 1)
a
loga b
b

9. ПРИМЕРЫ

1) 0,5
2)
5
5
2log5 3
log5 3
log0,5 6
6 .
(( 5 ) )
3.
2 log5 3

10. Свойства логарифма

1. Логарифм единицы
log
1
0
a
2. Логарифм основания
log a 1
a

11. Свойства логарифма

3. Логарифм произведения равен
сумме логарифмов множителей:
log xy log x log y
a
a
a

12. Свойства логарифма

4. Логарифм частного равен
логарифмов делимого без логарифма
делителя:
x
log
log x log y
a y
a
a

13. Свойства логарифма

5.1. Логарифм степени равен
произведению показателя степени на
логарифм ее основания:
5.1) log x
a
p
p log a x.

14. Свойства логарифма

5.2. При возведении основания в
некоторую (не нулевую) степень логарифм
делится на этот показатель степени:
1
5.2) log p b log a b.
a
p

15. Свойства логарифма

6. Логарифм корня равен отношению
логарифма подкоренного выражения и
показателя корня:
log
b
m
a
log а b
m

16. Свойства логарифма

7. Переход от одного основания к
другому
log b
c
log b
a
log a
c

17. Следствия

1
1) log b
a
log a
b
3) log
2) log
b
log
a
am
a
n
b
b
n
log a b.
m

18.

Свойства логарифмов: ПРИМЕРЫ
• 1. Вычислить: log612 + log63
Решение:
log612 +log63 = log6(12*3) = log636 = log662 = 2
Ответ: 2.
• 2. Вычислить: log5250 – log52.
Решение:
log5250 – log52 = log5(250/2) = log5125 = 3
Ответ: 3.
• 3. Вычислить: 27 log3 2
Решение:
3 log3 2
log3 8
log3 2
=
3
3
8
27
Ответ: 8.
18

19. Натуральный и десятичный логарифмы.

Десятичным называется логарифм,
основание которого равно 10.
Обозначается lg b, т.е. lg b=log10 b.
Натуральным называется логарифм,
основание которого равно e.
Обозначается ln b, т.е. ln b=loge b.

20. Свойства натуральных логарифмов

Чтобы по известному десятичному логарифму числа х найти
его натуральный логарифм, нужно разделить десятичный
логарифм числа х на десятичный логарифм числа е:
lg x
lg x
ln x
2.30259 lg x
lg e 0.43429
Чтобы по известному натуральному логарифму числа х
найти его десятичный логарифм, нужно умножить
натуральный логарифм числа х на десятичный логарифм
числа е:
lg x lg e ln x 0.43429 ln x
Число lg e=0.43429 называется модулем
десятичных логарифмов и обозначается через М.

21. Решение упражнений

22.

1) log 5 16 log 2 25
Воспользуемся сначала свойством log a b n n log a b
log 5 2 log 2 5 4 log 5 2 2 log 2 5
4
2
Теперь перейдем к основанию 2
1
8
log 2 5 8
log 2 5
log a b
1
log c a

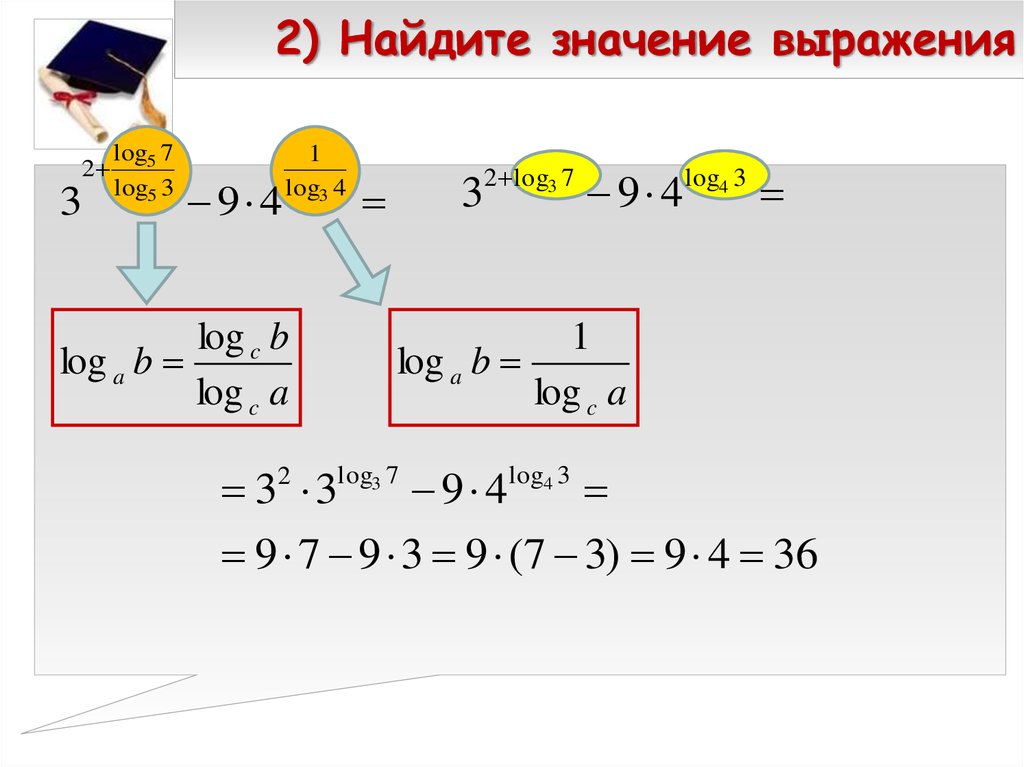
23. 2) Найдите значение выражения

2
3
log5 7
log5 3
9 4
1
log3 4
log c b
log a b
log c a
2 log3 7
3
9 4
log4 3
1
log a b
log c a
3 3
9 4
9 7 9 3 9 (7 3) 9 4 36
2
log3 7
log4 3

24. 3)Найдите значение выражения , если

Решение:
log a (a b ) log a a log a b
5
2
5
2
1
7
5 2
5 2 12
log b a
2
Ответ: 12
1
log a b
log c a