Понятие логарифма. Логарифм и его свойства

1. ПОНЯТИЕ ЛОГАРИФМА

Восточно-Казахстанский технологический колледж
ПОНЯТИЕ ЛОГАРИФМА
Логарифм и его
свойства
СРС
Подготовил: Муратов
Ерсин,13ОП
Семей 2017

2. Для чего были придуманы логарифмы? Кто является изобретателем логарифмов?

Конечно же, для ускорения и упрощения
вычислений.
Изобретатель первых логарифмических
таблиц шотландский математик
Джон Непер

3. Джон Непер

«Я старался,
насколько мог и умел,
отделаться от
трудности и скуки
вычислений,
докучность которых
отпугивает весьма
многих от изучения
математики»

4. Определение логарифма

Логарифмом числа в>0 по основанию а,
где а>0 и а 1, называется показатель
степени х, в которую нужно возвести
число а, чтобы получить число в.
log a b x, a b
x

5. Запомни

log а а 1 log 1 а 1
а
1
log а 1 0 log а 1
а

6. Вычислить:

log 2 8 3
log 1 9 2
3
1
log 4 2
16
2 8
3
2
1
9
3
2
4 16

7. Основное логарифмическое тождество

а
log а в
в
Например,
5
log5 25
25

8. Свойства логарифмов

Логарифм произведения положительных
чисел равен сумме логарифмов
сомножителей:
log a ( x1 * x2 ) log a x1 log a x2
log 12 2 log 12 72 log 12 144

9. Свойства логарифмов

Логарифм частного положительных чисел
равен разности логарифмов делимого и
делителя:
x1
log a log a x1 log a x2
x2
log 5 35 log 5 7 log 5 5

10. Свойства логарифмов

Логарифм степени положительного
основания равен произведению
показателя степени на логарифм
основания степени:
log a x n * log a x
n

11. Свойства монотонности логарифмов

Если a>1 и
Сравнить:
x1 x2 ,
то log a x1 log a x2
log 3 5и log 3 15

12. Свойства монотонности логарифмов

Если 0 < а <1 и
x1 x2 ,
то log a x1 log a x2
Сравнить:
log 1 2и log 1 10
3
3

13. Формула перехода от логарифмов по одному основанию к логарифмам по другому основанию

log b c
log a c
log b a
log 2 2
log 32 2
log 2 32

14. Формула перехода от логарифмов по одному основанию к логарифмам по другому основанию

1
log a в
log в a
1
log 32 2
log 2 32

15. Десятичные логарифмы

Если основание логарифма равно 10, то
логарифм называется десятичным:
log10 в lg в

16. Десятичные логарифмы

чисел, выраженных единицей с
последующими нулями:
lg10 1
101 10
lg100 2
102 100
lg1000 3
103 1000
lg10000 4
104 10000

17. Десятичные логарифмы

чисел, выраженных единицей с
предшествующими нулями
lg 0,1 1
lg 0, 01 2
1
10 0,1
2
10 0, 01
lg 0, 001 3
10 0, 001
lg 0, 0001 4
10 4 0, 0001
3

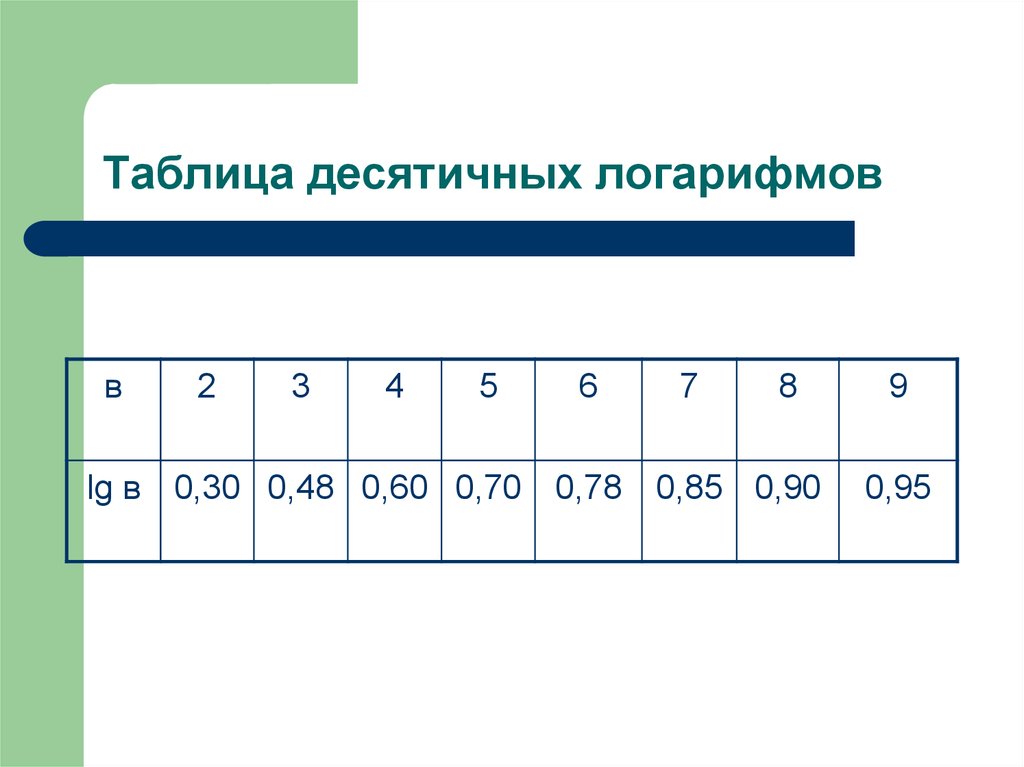
18. Таблица десятичных логарифмов

в
2
3
4
5
6
7
8
lg в 0,30 0,48 0,60 0,70 0,78 0,85 0,90
9
0,95

19. Натуральные логарифмы

Если основание логарифма е 2,7, то
логарифм называется натуральным:
log e в log 2,7 в ln в

20. Натуральные логарифмы

ln 2, 7 1
2, 7 2, 7
ln 7, 29 2
2, 7 2 7, 29
ln19, 683 3
2, 73 19, 683
ln 53,1441 4
2, 7 53,1441
1
4

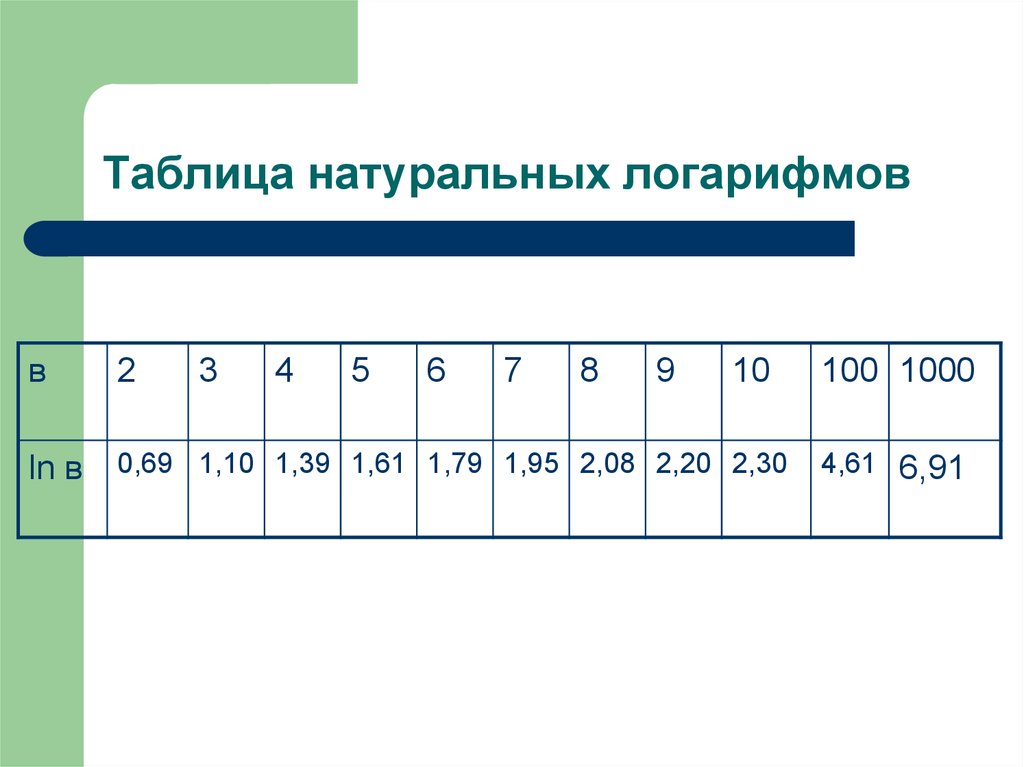
21. Таблица натуральных логарифмов

в
2
ln в
0,69 1,10 1,39 1,61 1,79 1,95 2,08 2,20 2,30
3
4
5
6
7
8
9
10
100 1000
4,61 6,91

22. Логарифмирование алгебраических выражений

Если число х представлено
алгебраическим выражением, то
логарифм любого выражения можно
выразить через логарифмы
составляющих его чисел.
(на основании свойств логарифмов)

23. Прологарифмировать алгебраическое выражение:

Пример:
а *в
х
2
с
3
a *в
lg x lg(
)
2
с
3
2
lg x lg( a * в ) lg c
3
lg x lg a lg в lg c
3
2
lg x lg a 3 lg в 2 lg c

24. Потенцирование логарифмических выражений

Переход
от логарифмического
выражения к алгебраическому
называется потенцированием, то
есть, произвести действие,
обратное логарифмированию

25. Перейти к алгебраическому выражению

lg x lg a 2 lg в lg c
lg x lg a lg в 2 lg c
lg x lg( a * в ) lg c
2
a *в
lg x lg(
)
c
a * в2
x
с
2