Системы автоматического управления (САУ). Теория автоматического управления (ТАУ)

1.

2.

3.

4.

5.

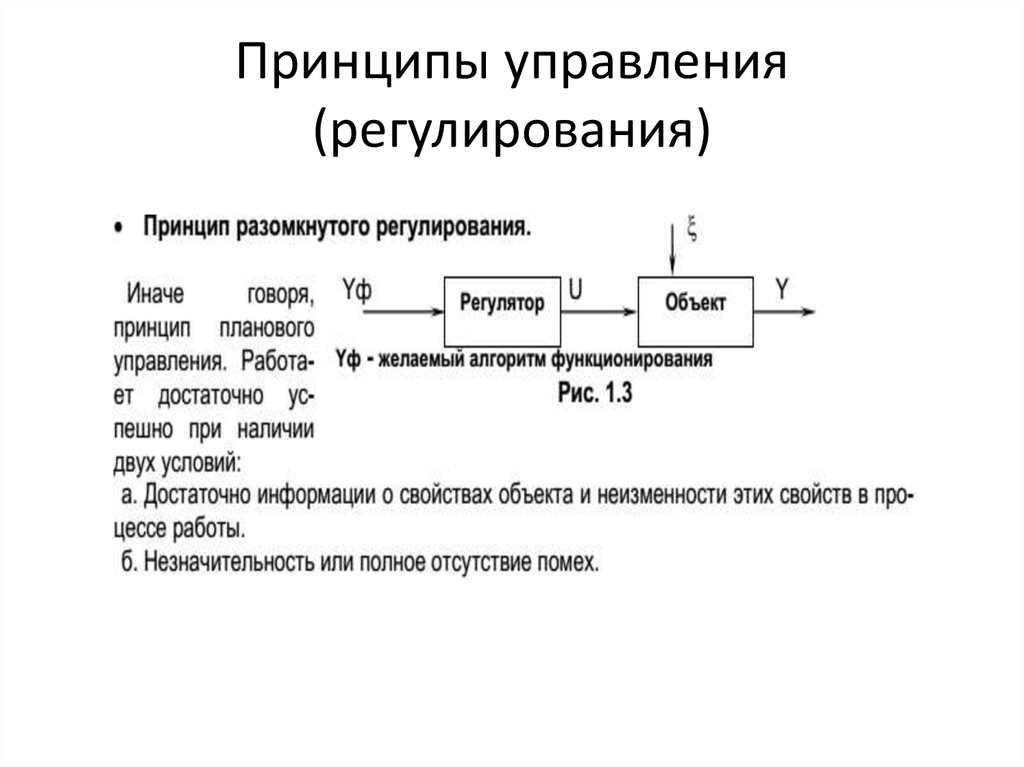
6. Принципы управления (регулирования)

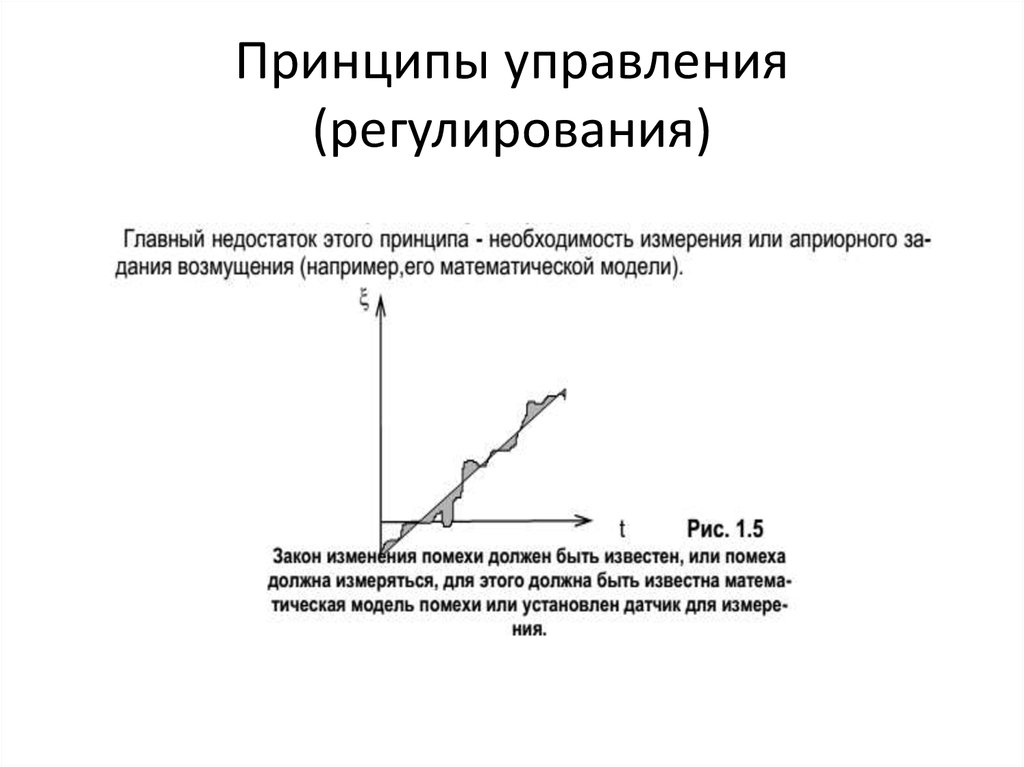
7. Принципы управления (регулирования)

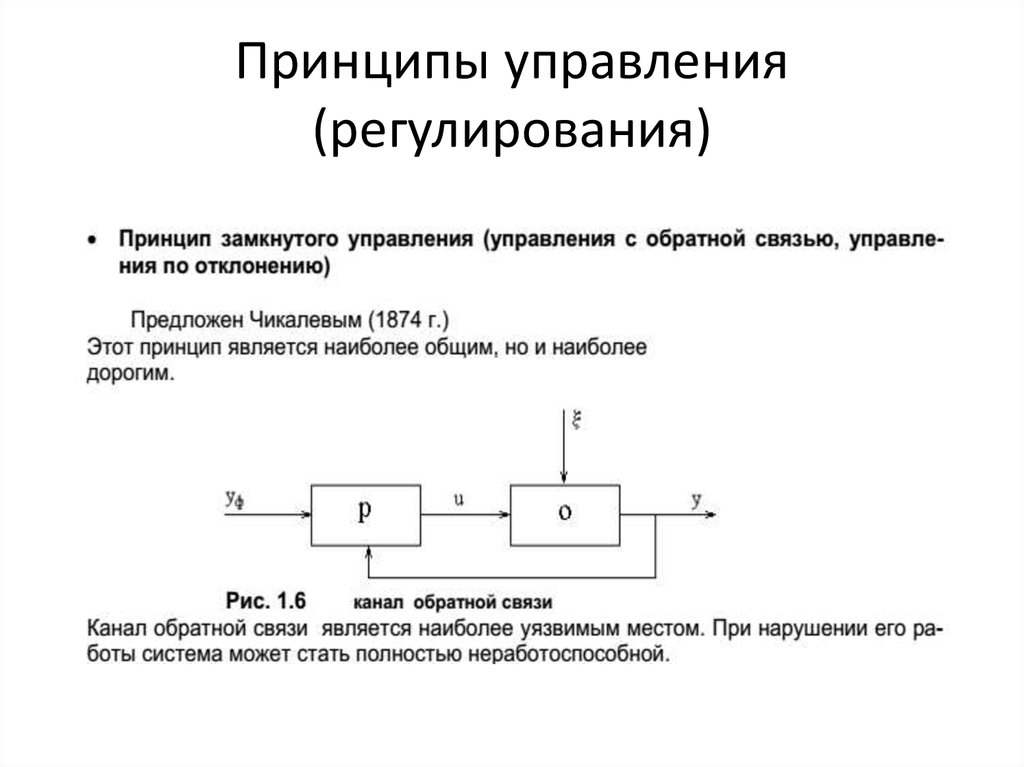
8. Принципы управления (регулирования)

9. Принципы управления (регулирования)

10. Принципы управления (регулирования)

11.

12.

13. ТИПЫ САУ

14. Типы САУ (примеры)

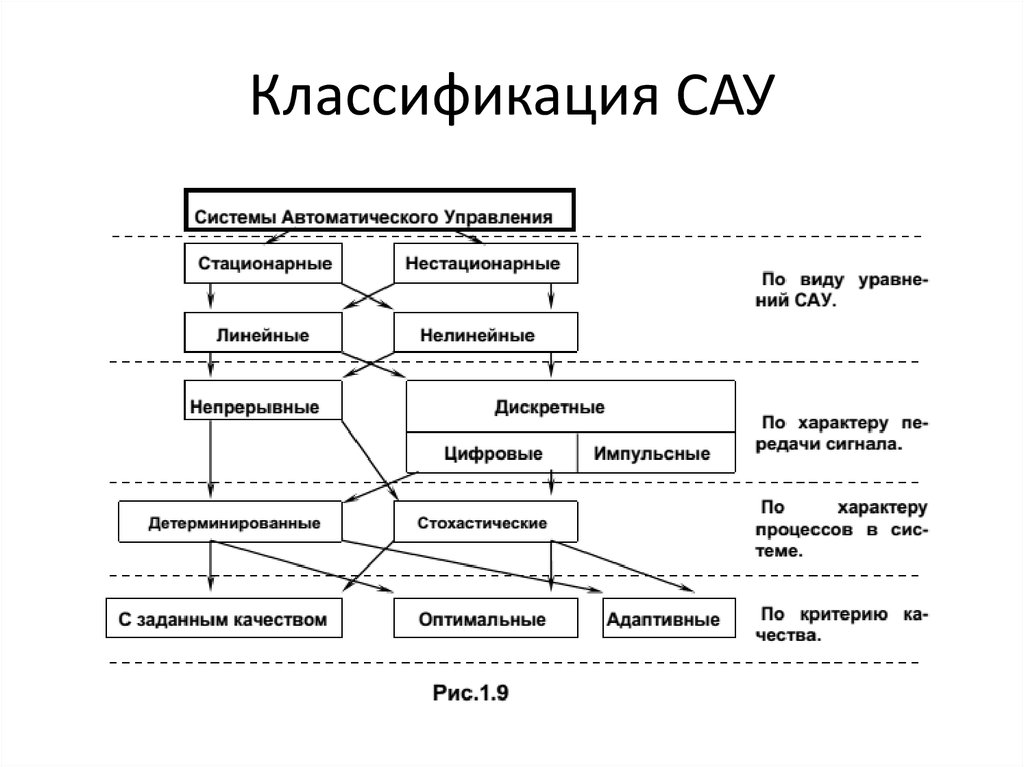
15. Классификация САУ

16. Преобразование Лапласа

17. Преобразование Лапласа.Основные свойства

18. Преобразование Лапласа. Основные свойства

19. Преобразование Лапласа. Основные свойства

20. Преобразование Лапласа. Основные свойства

21. Преобразование Лапласа. Основные свойства

22. Преобразование Лапласа.Основные свойства

23. Преобразование Лапласа. Основные свойства

24. Преобразование Лапласа.Основные свойства

25. Преобразование Лапласа. Основные свойства

26. Преобразование Лапласа.Основные свойства

27. Преобразование Лапласа.Основные свойства

28. Преобразование Лапласа.Основные свойства

29. Преобразование Лапласа.Основные свойства

30. Преобразование Лапласа.Основные свойства

31. Преобразование Лапласа.Основные свойства

32. Отыскание оригиналов дробно-рациональных изображений

Отыскание оригиналов дробнорациональных изображений
• Для нахождения оригинала по известному
изображению , где есть правильная рациональная
дробь, применяют следующие приемы.
• 1. Эту дробь разлагают на сумму простейших
дробей и находят для каждой из них оригинал,
пользуясь свойствами преобразования Лапласа.
• 2. Находят полюсы этой дроби и их кратности .
Тогда оригиналом для будет функция F(p),
• где сумма берется по всем полюсам функции .

33. Отыскание оригиналов дробно-рациональных изображений

Отыскание оригиналов дробнорациональных изображений
• (16)

34. Отыскание оригиналов дробно-рациональных изображений

Отыскание оригиналов дробнорациональных изображений
• В случае, если все полюсы функции
простые, т.е. , последняя формула
упрощается и принимает вид
• (17)

35. Пример 1.

• Найти оригинал функции f(t), если

36. Решение. Первый способ (сл1).

• Представим в виде суммы простейших
дробей
и найдем неопределенные коэффициенты
A,B,C,D.

37. Решение. Первый способ (сл2).

• Имеем
Полагая в последнем равенстве
последовательно
• получим

38. Решение. Первый способ (сл3).

• откуда

39. Решение. Второй способ. (сл1)

• Найдем полюсы
функции
Они совпадают с нулями знаменателя
Таким образом, изображение
Пользуясь формулой
получаем оригинал
имеет четыре простых полюса

40. Пример 2.

• Найти оригинал
если

41. Решение примера 2.

• Данная дробь
имеет полюс
кратности
• и полюс
кратности
• . Пользуясь формулой (16)
• получаем оригинал