Похожие презентации:
Интегральное исчисление. Лекция 2
1. Лекция 2. интегральное исчисление
ЛЕКЦИЯ 2. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕПервообразная, неопределенный
интеграл.
Методы интегрирования.
Определенный интеграл по отрезку.
Формула Ньютона –Лейбница.
Несобственные интегралы.
Приближенное вычисление интегралов
2. Понятие неопределенного интеграла
ПОНЯТИЕ НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛАВ дифференциальном исчислении решается задача: по
данной функции найти ее производную. Интегральное
исчисление решает обратную задачу: найти функцию,
зная ее производную. Искомую функцию называют
первообразной.
Функция F(x) называется первообразной функции f(x) на
интервале (а,b), если для любого x (а,b) выполняется
равенство F‘(x) = f(x)
Теорема. Если функция F(x) является первообразной
функции f(x) на (а,b), то множество всех первообразных
для f(x) задается формулой, F(x)+C, где С = const
3. Понятие неопределенного интеграла
ПОНЯТИЕ НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛАМножество всех первообразных функций F(x)+С для
f(x) называется неопределенным интегралом от
функции f(x)
න f(x) dx=F(x)+С
f(x) называется подынтегральной функцией,
х — переменной интегрирования
Операция нахождения неопределенного интеграла от
функции называется интегрированием этой функции
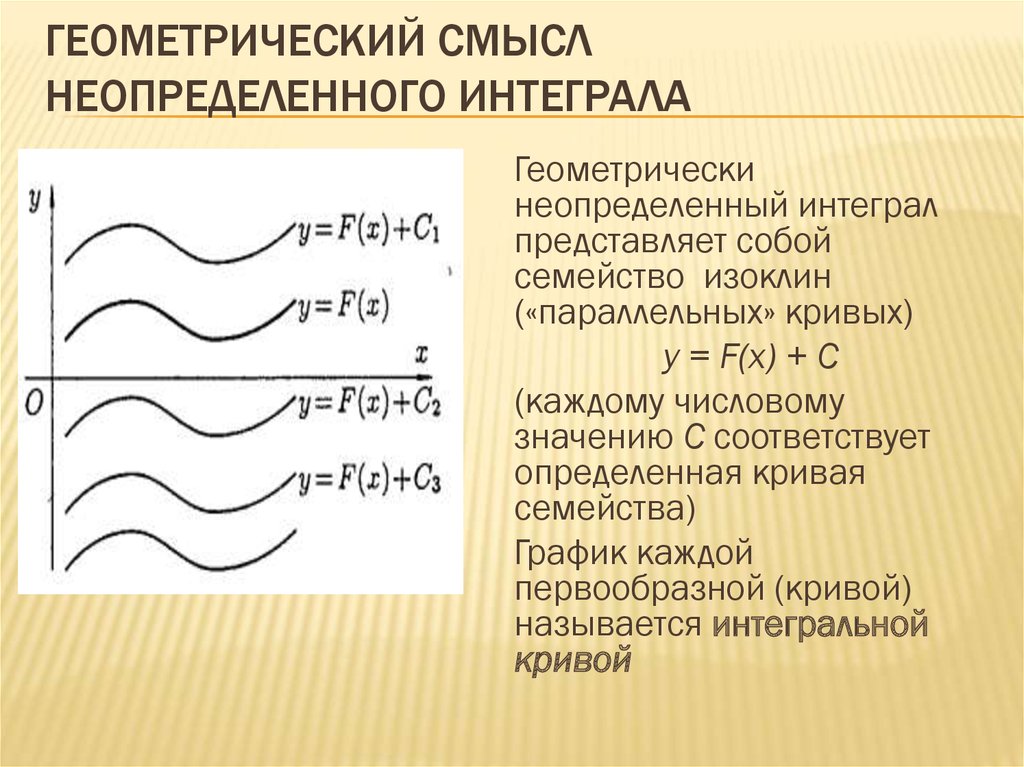
4. Геометрический смысл неопределенного интеграла
ГЕОМЕТРИЧЕСКИЙ СМЫСЛНЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Геометрически
неопределенный интеграл
представляет собой
семейство изоклин
(«параллельных» кривых)
у = F(x) + C
(каждому числовому
значению С соответствует
определенная кривая
семейства)
График каждой
первообразной (кривой)
называется интегральной
кривой
5. свойства неопределенного интеграла
СВОЙСТВА НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛАпроизводная неопределенного интеграла равна
подынтегральной функции:
(න

















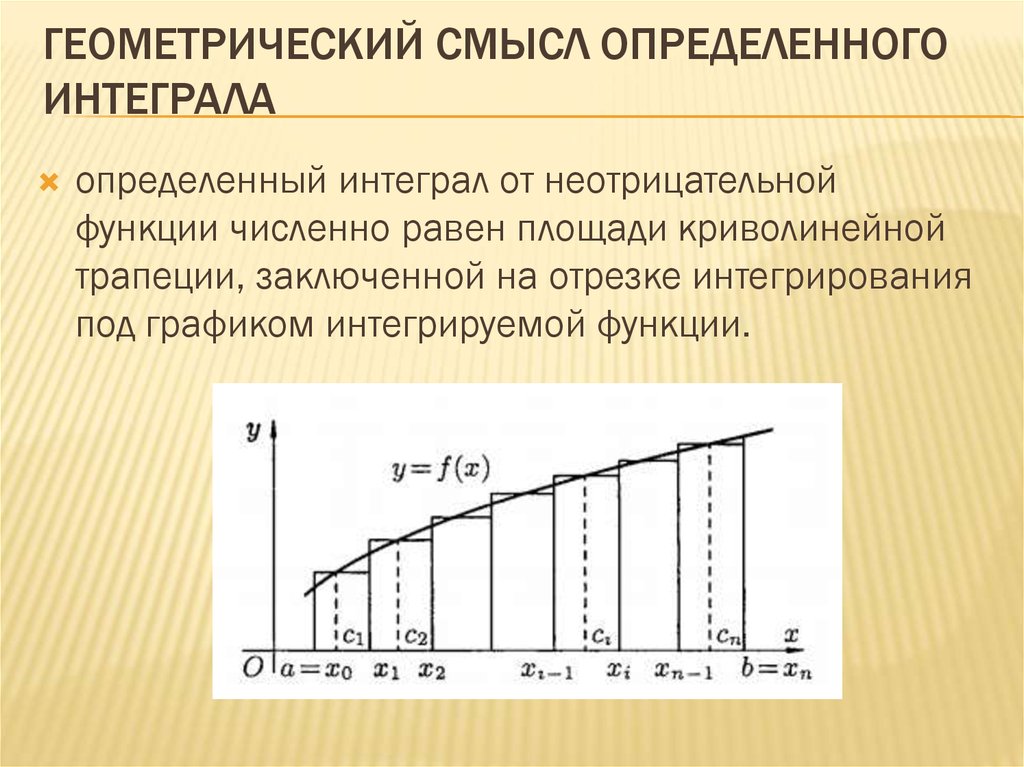











 Математика
Математика








