Похожие презентации:
Дифференциальное и интегральное исчисление
1. лекция № 5 для студентов 1 курса, обучающихся по специальности 030401– Клиническая психология к.п.н., доцент Шилина Н.Г. Красноярск, 2015
Кафедра медицинской и биологической физикиТема: Дифференциальное и интегральное исчисление.
лекция № 5 для студентов 1 курса, обучающихся по
специальности 030401– Клиническая психология
к.п.н., доцент Шилина Н.Г.
Красноярск, 2015
2. План лекции
• Дифференциал функции. Геометрический смыслдифференциала.
• Частные производные. Полный дифференциал.
• Понятие первообразной функции. Неопределенный
интеграл.
• Методы интегрирования (по формулам, заменой
переменной, по частям).
• Задачи, приводящие к понятию определенного
интеграла.
• Формула Ньютона-Лейбница.
• Применение определенного интеграла для
вычисления площадей криволинейных фигур.
3. Значение темы
• Понятие производной и интегралашироко используется в математике,
статистике и прикладных науках. С их
помощью определяют скорости
изменения функций, функции
распределения, вычисляют площади,
ограниченные кривыми.
4. Понятие производной
Производной функции f(x) называетсяпредел отношения приращения функции к
приращению аргумента при стремлении
последнего к нулю, т.е.
y
y lim
x 0 x
5. Правила дифференцирования производная сложной функции
(U V ) U V(U V ) U V V U
С 0
(С U ) C U
U U V V U
2
V
V
у f z ( x )
y f z z x
6. Таблица производных от основных функций
ФункцияПроизводная
xn
n∙xn–1
ax
ax∙lna
ex
ex
logax
1
x ln a
lnx
1
x
sin(x)
cos(x)
cos(x)
– sin(x)
7.
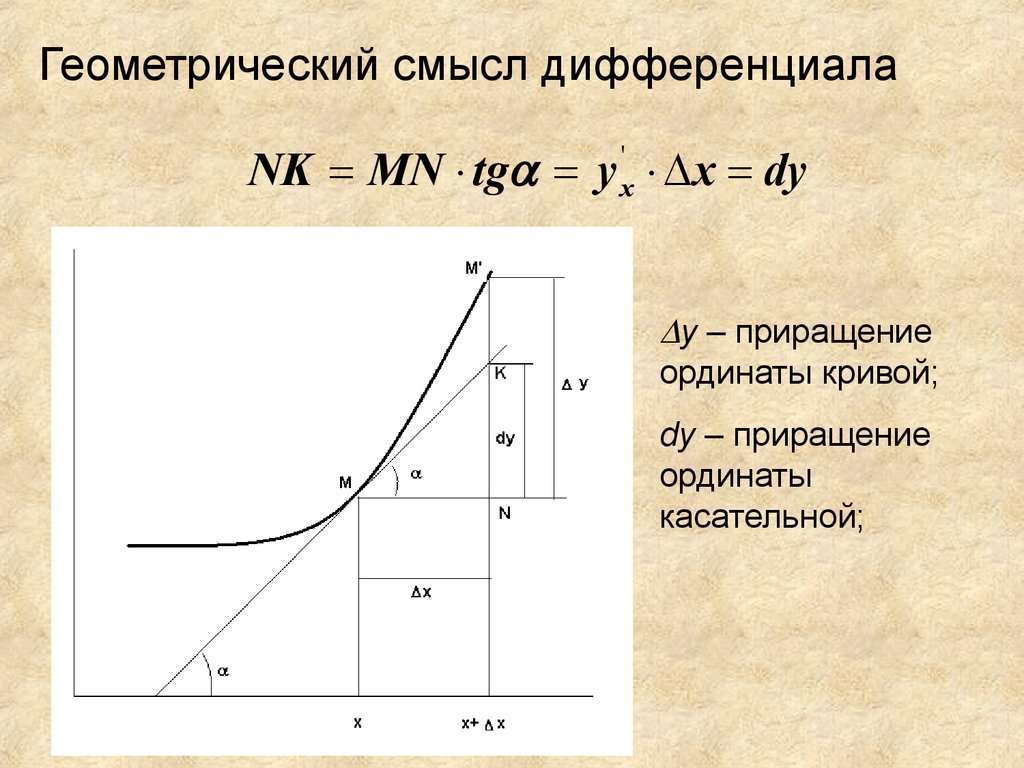
Геометрический смысл дифференциалаNK MN tg y x dy
'
x
y – приращение
ординаты кривой;
dy – приращение
ординаты
касательной;
8. Дифференциал
Дифференциал dy - главная часть приращенияфункции y
Дифференциалом dx называют приращение x, то
есть dx= x
dy y dx
'
x
dy
y
dx
'
x
9. Правила дифференцирования
d (cu) c dud (u v ) du dv
d (uv ) u dv v du
u v du u dv
d
2
v
v
10. Частные производные
z f ( x, y )x z f ( x x , y ) f ( x , y )
y z f ( x , y y ) f ( x , y )
z
z
f ( x x , y ) f ( x , y )
lim x lim
x x 0 x x 0
x
z
z
f ( x, y y ) f ( x, y )
z y
lim y lim
y y 0 y y 0
y
z x
dxz
z
dx
x
dyz
z
dy
y
z
z
dz d x z d y z
dx
dy
x
y
11. Использование дифференциала в приближенных вычислениях
• Длянахождения
приближенного
значения приращения функции
y dy y dx
• Для
нахождения
приближенного
значения функции в заданной точке
f ( x x ) f ( x ) f x dx
• Для вычисления погрешностей
N абс dN ; N отн
dN абс
N
12. Основные характеристики и свойства функции Y=f(X)
- Область значений y и х-Постоянство или монотонность функции на отрезке
- Нули функций
- Разрывы и полюса функции
- Экстремумы, минимумы и максимумы функции
- Перегибы функции
- Асимптоты функции
- Вогнутость и выпуклость функции
13. Постоянство и монотонность функции
Для того чтобы функция f(x) была постоянной наотрезке [a,b], нужно, чтобы производная этой
функции была равна нулю на этом отрезке.
Для того, чтобы функция f(x) была монотонной на
отрезке [a,b], нужно чтобы производная не меняла
своего знака на этом отрезке и не обращалась
тождественно в нуль ни в какой точке или
промежутке, составляющем часть отрезка.
14.
Нули функции: решения уравнения Y(X) =0Y aX b
aX b 0
b
X0
a
Полюса функции: значения
Х, при котором Y стремится
к бесконечности
k
X a
когда X a, и X a, Y ;
когда X a, и X a, Y
Y
15. Минимумы и максимумы функции
Функция f(x) имеет в точке х0 минимум (максимум), если внекоторой окрестности этой точки ее значения больше
(меньше) значения f(x0)
Экстремум = минимум или максимум
Необходимое, но недостаточное условие существования
экстремума: экстремум функции достигается в точках, где
значение производной равно нулю.
Контр-пример:
y x 3 ; y 2 x 2 ; y ( x 0) 0
Достаточное условие:
Если первая производная в точке х0 равна нулю, а вторая
производная - больше нуля, то функция имеет минимум;
Если первая производная в точке х0 равна нулю, а вторая
производная меньше нуля, то функция имеет максимум
16. Правило нахождения экстремума
y f ( x)dy ( x0 )
d 2 y ( x0 )
0;
0 в точке x 0 минимум ;
2
dx
dx
dy(x 0 )
d 2 y ( x0 )
0;
0 в точке x 0 максимум
2
dx
dx
17. Перегибы, выпуклость и вогнутость функции
Если вторая производная в точке М большенуля, то кривая в той точке вогнутостью
направлена вверх.
d 2 f ( x0 )
0
2
dx
Если вторая производная в точке М меньше
нуля, то кривая в той точке вогнутостью
направлена вниз.
d 2 f ( x0 )
0
2
dx
Если вторая производная в точке М равна
нулю, то М – точка перегиба
d 2 f ( x0 )
0
2
dx
18. Первообразная функции
Прямая задача: известно уравнение движения s=s(t);найти скорость v=ds/dt и ускорение dv/dt
Обратная задача: задана функция ускорения a=a(t),
требуется определить скорость v и пройденный путь s
Интегрирование: зная функцию a(t), восстановить функцию
v=v(t), для которой a(t) является производной.
Функция F(x) называется первообразной функцией для
функции f(x) или интегралом от f(x), если f(x) является
производной для функции F(x), или, что то же самое, f(x)dx
служит для F(x) дифференциалом.
F ( x ) f ( x ) или dF(x) f(x)dx
F ( x ) f ( x ) dx
19. Свойства операции интегрирования
dF ( x ) F ( x ) Cdx x
cf ( x)dx c f ( x )dx
[ f ( x ) g ( x )]dx f ( x )dx g ( x )dx
Закон инерции Ньютона: как, зная уравнение
для второго закона Ньютона, найти уравнение
для скорости тела?
v
adt a dt at C
dv F
a
dt m
20. Таблица интегралов основных функций
x n 1x dx n 1 c, n 1
n
x
a
x
a
dx ln a с
dx
x ln x с
x
x
e
dx
e
c
cos xdx sin x c
sin xdx cos x c
dx
cos 2 x tgx c
dx
sin 2 x ctgx c
21. Пример:
(6
x
3
x
5
)
dx
2
6 x dx 3 x dx 5dx
2
3
2
x
x
6 x 2 dx 3 xdx 5 dx 6 3 5 x C
3
2
22. Интегрирование путем замены переменной
3sin
x cos xdx
d sin x cos x dx
t sin x
sin 3 x cos x dx sin 3 x d sin x t 3 dt
4
4
t
sin
x
3
t dt 4 C 4 C
23. Интегрирование по частям
udv uv vdux cos x dx ?
u x; dv cos x dx; du dx; v sin x
x cos x dx x d sin x x sin x sin x dx x sin x cos x C
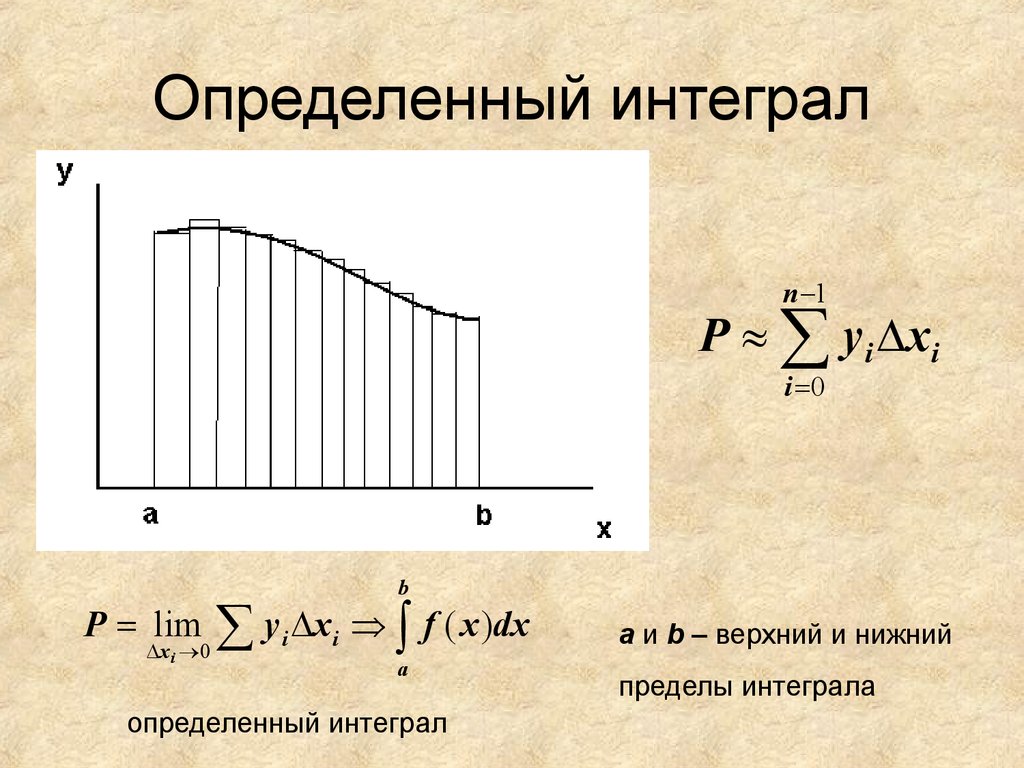
24. Определенный интеграл
n 1P y i x i
i 0
P lim
x i 0
y x
i
b
i
f ( x )dx
a
определенный интеграл
a и b – верхний и нижний
пределы интеграла
25. Свойства определенного интеграла
ba
f ( x) dx f ( x ) dx
a
b
a
f ( x ) dx 0
a
b
c
b
a
a
c
f ( x ) dx f ( x ) dx f ( x ) dx
26. Основная формула интегрального исчисления
b( x ) f ( x ) dx ?
a
F ( x ) f ( x ) dx
F(x) – первообразная f(x)
b
( x ) f ( x ) dx F (b) F (a )
a
1 b
1
1
x
b
a
x
a dx 1 1
a
b
27. Площадь фигуры
bf
(
x
)
g
(
x
)
dx
a
28. РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА:
Обязательная:
Кричевец, А.Н. Математика для психологов /А.Н. Кричевец, Е.В. Шикин,
А.Г. Дьячков. – М.: Флинта: НОУ ВПО «МПСИ», 2010.– 376 с.
Наследов А.Д. Математические методы психологического исследования.
Анализ и интерпретация данных/А.Д. Наследов.-СПб.: Речь, 2008.
Дополнительная:
Математика в примерах и задачах: учебное пособие /Л.Н.Журбенко, Г.А.
Никонова, Н.В.Никонова и др. – М.: ИНФРА–М, 2011. –373 с.
Болдин К.В., Башлыков В.Н., Рукосуев А.В. Высшая математика /К.В.
Болдин К, В.Н. Башлыков, А.В. Рукосуев. – М.: Флинта, 2010
Электронные ресурсы:
УБИЦ КрасГМУ Портал центра дистанционного образования
Электронная библиотека
Ресурсы интернет



















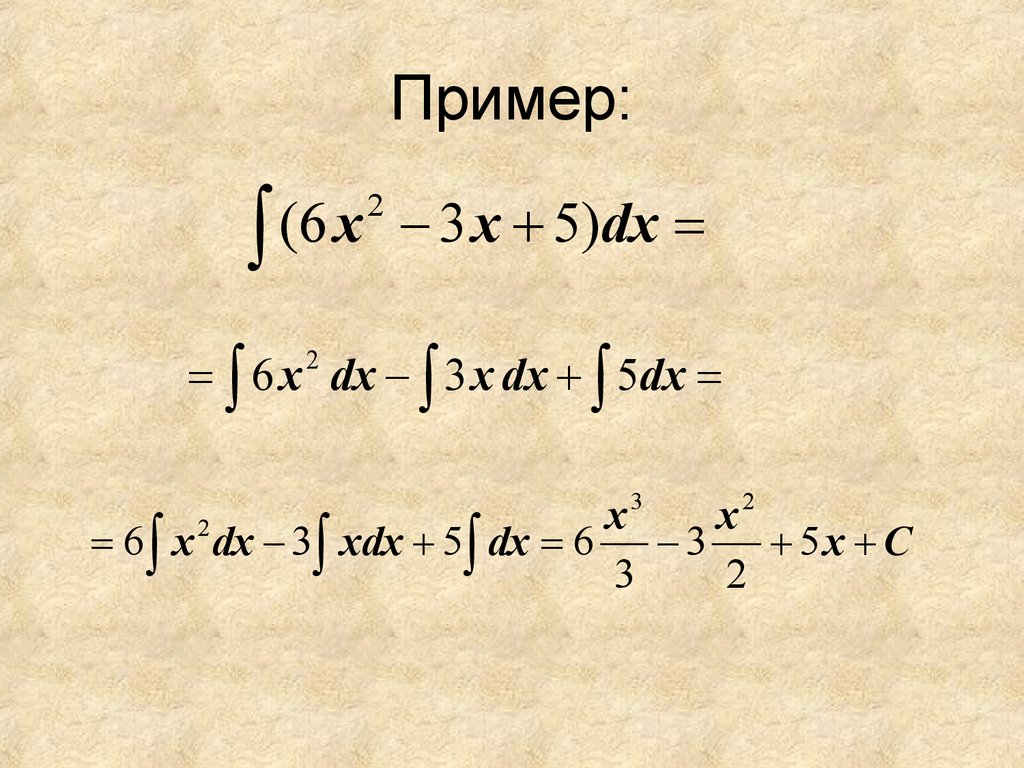







 Математика
Математика








