Элементы квантовой механики

1.

ЭЛЕМЕНТЫ КВАНТОВОЙ
МЕХАНИКИ

2.

Гипотеза де Бройля
В 1924 г. Луи де Бройль выдвинул
гипотезу об универсальности
корпускулярно-волнового дуализма:
не только фотоны, но и любые
частицы материи наряду с
корпускулярными обладают также
и волновыми свойствами.

3.

Связь величин, описывающих
корпускулярные и волновые свойства
частиц та же, что и для фотонов:
h
h
p mv

4.

Групповая и фазовая скорости волн де Бройля
Условно представим каждую частицу
в виде волнового пакета, центр которого
соответствует центру частицы.

5.

Фазовая:
vфаз
2
2
E mc
c
c
c c
k
k
p mv v
v
Фазовая скорость волн де Бройля больше
скорости света.
Групповая:
d dE pc
mv c
u
v
2
dk dp
E
mc
2
2
Групповая скорость волны де Бройля равна
скорости частицы.

6.

Длина волны де Бройля тем
меньше, чем больше масса
частицы и ее скорость.
Пусть m = 1 г, v = 1 м/с, тогда
10
30
м.
Волновые свойства никак не
проявляются в механике
макроскопических тел.

7.

Для электрона с энергиями от 10 эВ
до 104 эВ длины волн де Бройля
лежат в интервале
(0,1 10) 10
10
м,
как для рентгеновского излучения.
Для таких электронов должна
наблюдаться дифракция на
кристаллах.

8.

Первое экспериментальное
подтверждение гипотезы де Бройля было
получено в 1927 году в опытах
К. Дэвиссона и Л. Джермера.
Было установлено, что электроны
дифрагируют на кристалле никеля,
причем именно так, как должно быть для
волн, длина которых определяется
соотношением де Бройля.

9. Опыт В.А. Фабриканта (1949 г.)

10. Дифракция электронов при прохождении через очень тонкий слой серебра

11. Дифракция нейтронов

11

12.

Природа волн де Бройля
Это не электромагнитные волны.
Природа волн де Бройля
вероятностная. Частицы с
большей вероятностью
оказываются в тех местах, где
больше интенсивность волн де
Бройля.

13.

Соотношение
неопределенностей
Гейзенберга

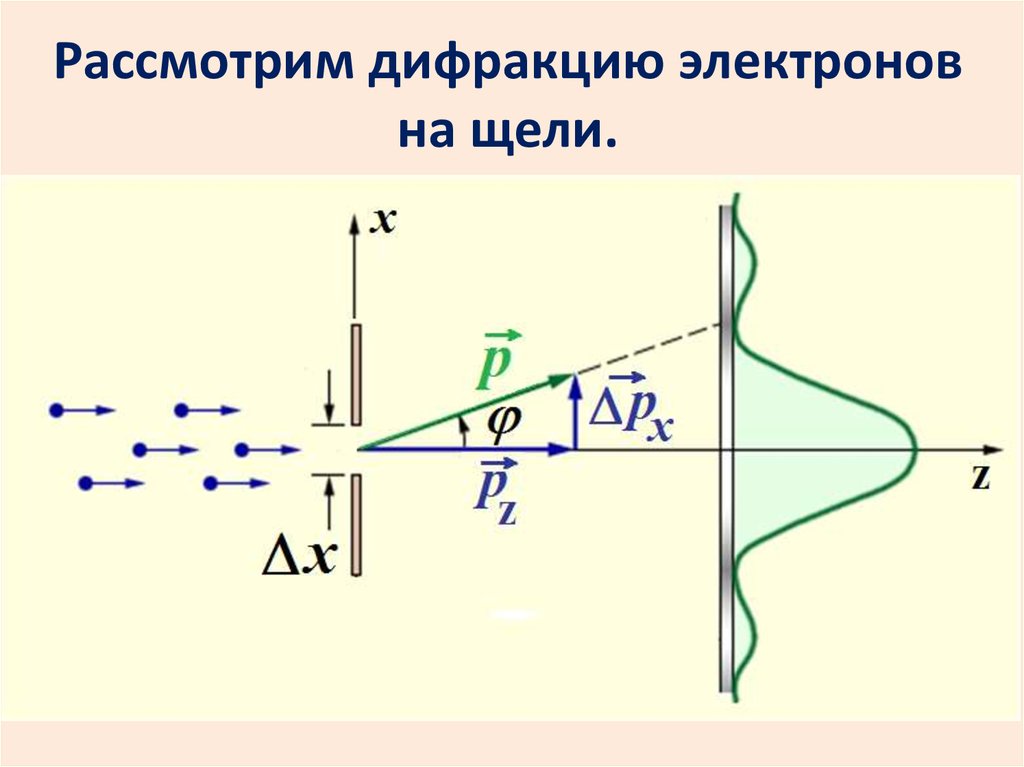
14. Рассмотрим дифракцию электронов на щели.

15.

Пусть условно все электроны
летят в центральный максимум.
Координата х каждого электрона
точно не известна. Неопределенность
координаты равна ширине щели х.
Компонента импульса по х также
неизвестна. Запишем ее как рх.

16.

Запишем условие первого минимума:
b sin m ( m 1)
x sin
p x
h
, a sin
p
p

17.

Получим:
p x h
x
или x p x h
p
p
С учетом других максимумов
произведение x px будет
больше.

18.

Соотношения неопределенностей
Гейзенберга:
x p x
y p y
z pz

19.

Для квантовой частицы
неправомерно говорить об
одновременных значениях ее
координаты и импульса. Чем точнее
определена какая-либо из координат,
тем больше неопределенность в
определении импульса (или скорости)
в том же направлении, и наоборот.
Понятие траектории для
квантовой частицы теряет смысл.

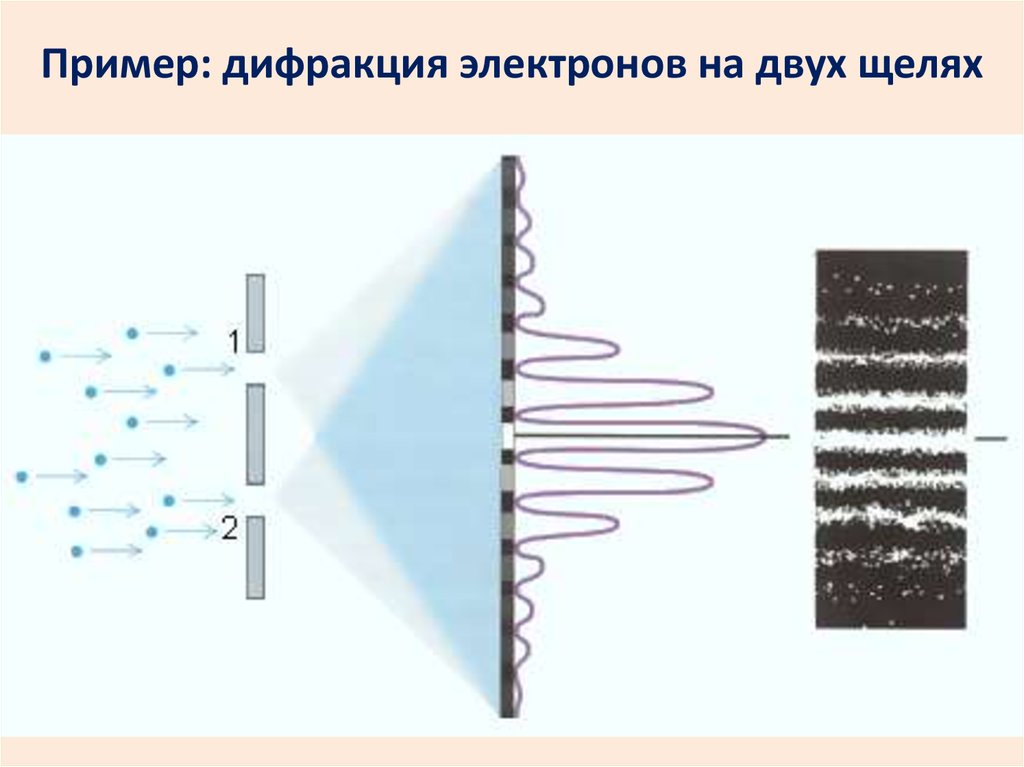
20. Пример: дифракция электронов на двух щелях

21.

В привычном мире все тела движутся по траекториям. Траекторию летящего электрона указать
невозможно: он не только частица, но и волна,
бесконечная в пространстве. Поэтому удается
только выяснить, какова вероятность обнаружить
электрон в том или ином месте. В какое отверстие электрон пролетел, сказать тоже нельзя:
можно считать, что он пролетел сквозь все
отверстия сразу!

22.

Для энергии частицы W и времени:
W t .
Эта неопределенность приводит к
размыванию уровней энергии
электронов в атомах, а, значит,
к уширению спектральных
линий.

23.

Волновая функция

24.

Положение частицы в
пространстве в данный момент
времени определяют с
помощью волновой функции
( x , y , z, t ).
Это комплексная величина.

25.

Вероятность dP того, что частица
находится в некоторм объеме dV:
2
dP dV
2
комплексно сопряженная
функция

26.

Квадрат модуля пси-функции дает
плотность вероятности положения
частицы в пространстве
dP
dV
2
и изменяется по волновому закону.

27.

Уравнение плоской волны де Бройля,
распространяющейся вдоль оси х:
( x, t ) Ae
i
Et px
р и Е – импульс и энергия частицы, i – мнимая
единица, А – амплитуда волны.
Учитывая, что E , p k получим:
( x , t ) Ae
i t kx

28.

( x , t ) Ae
i t kx
A
2
2
Квадрат амплитуды волны де Бройля в
данной точке является мерой вероятности
обнаружить частицу в этой точке. Это
аналогично формуле для интенсивности
света: I A2 .

29.

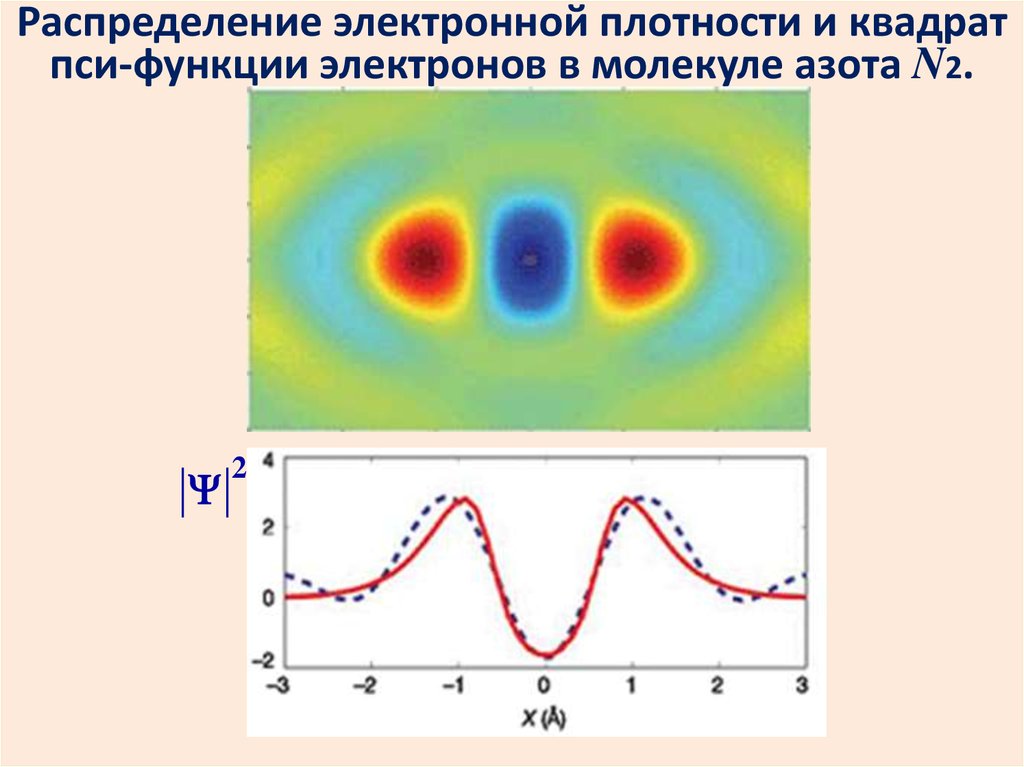
Распределение электронной плотности и квадрат
пси-функции электронов в молекуле азота N2.
2