Турнір з математики

1.

Знайти всі значення параметра р , при яких область визначення функції
складається з однієї точки
Область визначення даної функції задається системою нерівностей:
1 – х2 ≥ 0
х2 − р+3 х+3р
х+5
*(-1)
≥0
(х – 1) ˖ (х + 1) ≤ 0
х−р ˖ (х−3)
х+5
≤0
(1)
(2)
Нерівність (1) виконується при х є [-1;1].
Розв’яжемо нерівність (2). Є три різних випадки розміщення точок. х=-5; х=р; х=3.

2.

Зобразимо ці випадки на координатних прямих:
Зіставимо відрізок [-1; 1] із заштрихованими проміжками. Відрізок [-1; 1] може мати із
заштрихованими проміжками єдину спільну точку тільки у випадку, коли р = -1. Це
спіла точка є х = -1
Відповідь: р = -1.

3.

. Розв’язати рівняння
х+
х + 1 + {х} = 1
х +
1 + {х} = (1 - х)
ОДЗ:
1–х ≥0
[х] +
х ≤ 1
1 + {х} ≥ 0
1 + {х} ≥ - [х]
Отже, х ϵ [-1; 1]
1) х = 0 – корінь рівняння
2) якщо х ϵ (-1; 0), то [х] = -1
[х] + 1 + {х} = (1 – х)2
-1 + 1 + {х} = х2 – 2х + 1
1 + {х} = х2 – 2х +2
Оскільки х ϵ [-1;0), то
1 + {х} < 2 < 2 < х2 – 2х +2
Отже, на даному проміжку рівняння немає коренів.
х≤1
х ≥ -1

4.

1) Якщо х ϵ (0;1), то [х] = 0
0 + 1 + {х} = (1 – х)2
1 + {х} = (1 - х)4
1 + {х} ˃ 1, а (1 - х)4 ˂ 1
Отже, на даному проміжку рівняння немає розв’язків.
2) Коли х = 1, то [х] = 1; {х} = 0
1+ 1+ 1+0=1+ 2≠1
Отже, х = 1 – не є коренем рівняння.
Відповідь: х = 0

5.

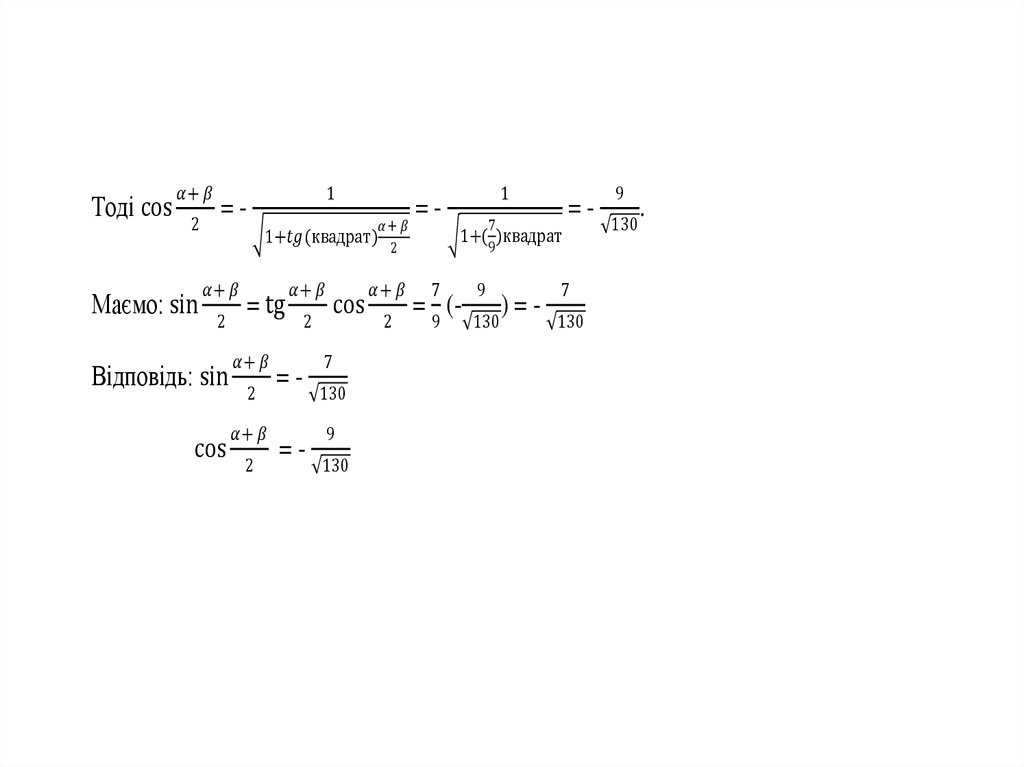
Обчислити sin
5