Гармонические колебания

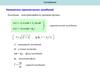
1. гармонические колебания

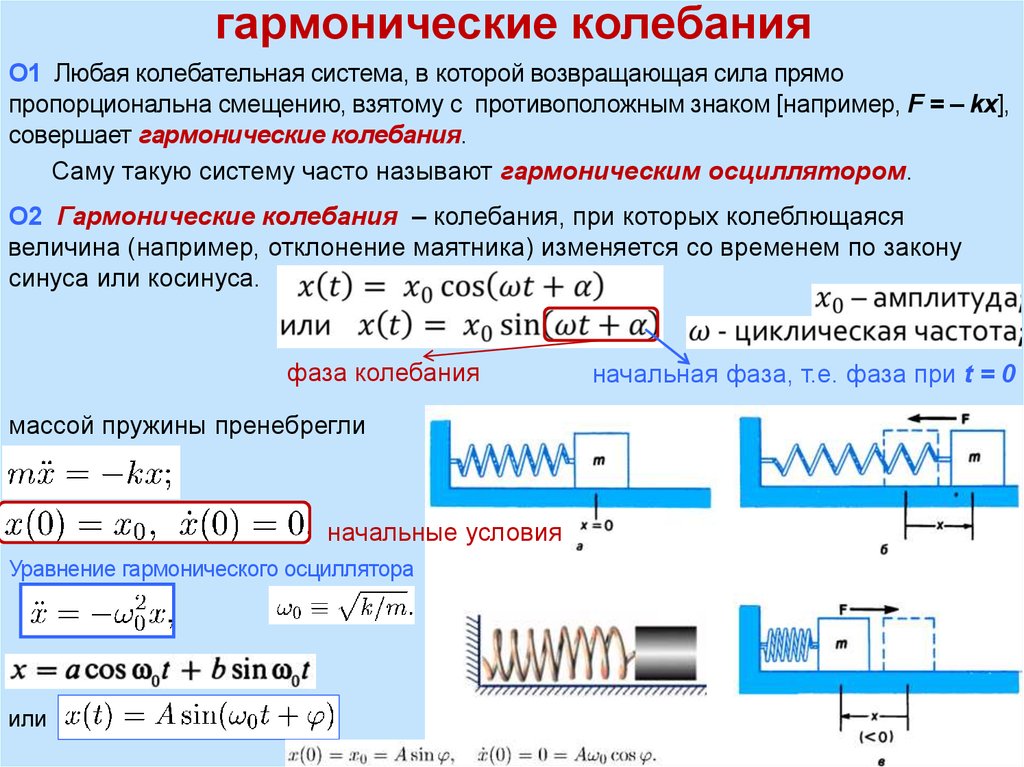
O1 Любая колебательная система, в которой возвращающая сила прямо
пропорциональна смещению, взятому с противоположным знаком [например, F = – kx],
совершает гармонические колебания.
Саму такую систему часто называют гармоническим осциллятором.
O2 Гармонические колебания – колебания, при которых колеблющаяся
величина (например, отклонение маятника) изменяется со временем по закону
синуса или косинуса.
фаза колебания
массой пружины пренебрегли
начальные условия
Уравнение гармонического осциллятора
или
начальная фаза, т.е. фаза при t = 0

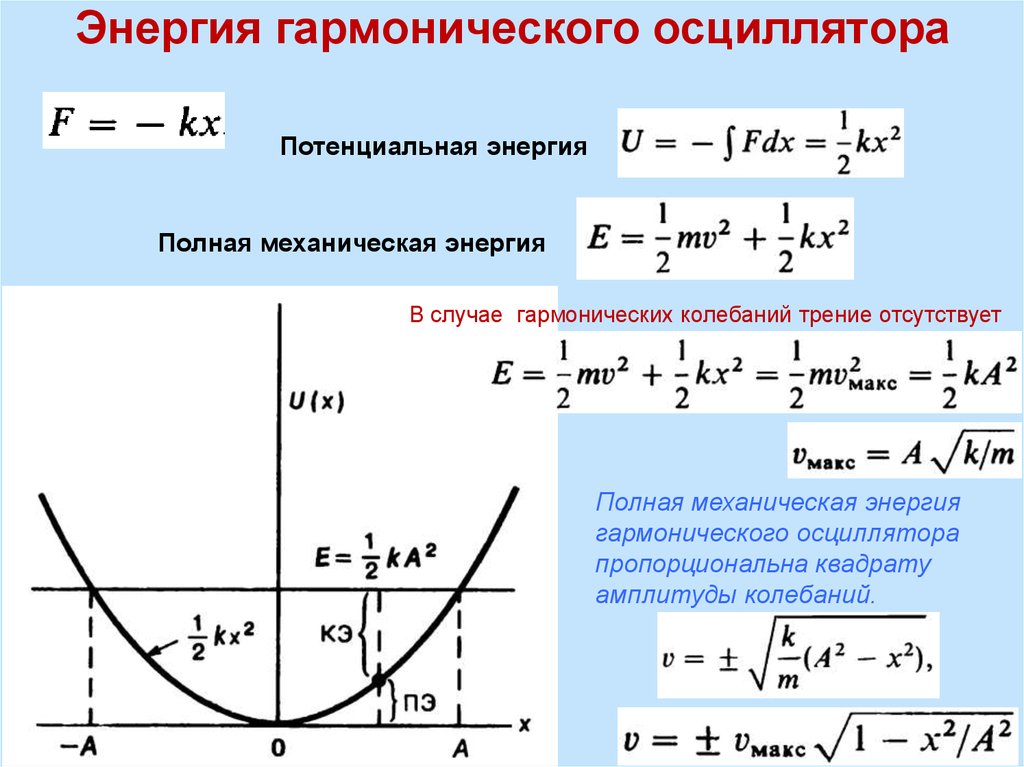
2. Энергия гармонического осциллятора

Потенциальная энергия
Полная механическая энергия
В случае гармонических колебаний трение отсутствует
Полная механическая энергия
гармонического осциллятора
пропорциональна квадрату
амплитуды колебаний.

3.

ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ

4.

СЛОЖЕНИЕ КОЛЕБАНИЙ

5.

Гармонические колебания в двух перпендикулярных
направлениях. Фигуры Лиссажу
Результирующая траектория движения в плоскости ху зависит от соотношения
частот, амплитуд и фаз этих колебаний.
Одинаковые частоты
Одинаковые фазы
Фазы различаются на π/2:

6.

ПЕРИОДЫ КОЛЕБАНИЙ МАЯТНИКОВ

7.

t=0
– постоянная затухания
τ–
время релаксации колебания.
амплитуда колебаний уменьшается в е раз
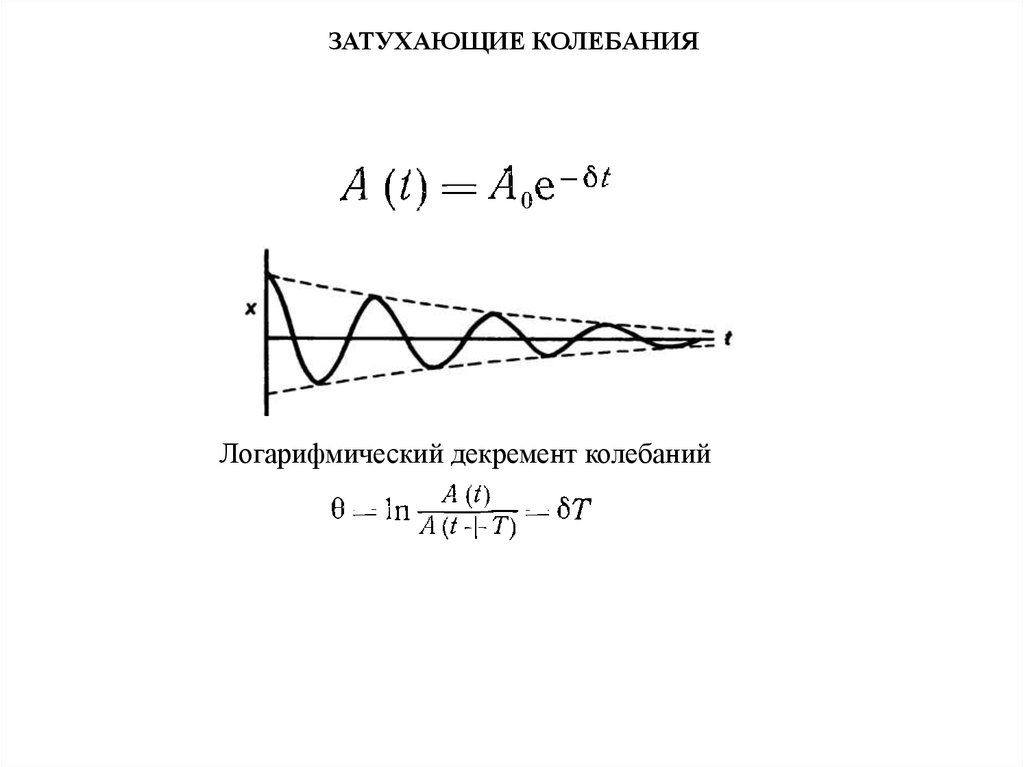
– логарифмический декремент затухания;
– добротность осциллятора

8.

ЗАТУХАЮЩИЕ КОЛЕБАНИЯ
Логарифмический декремент колебаний

9.

ЗАТУХАЮЩИЕ КОЛЕБАНИЯ

10.

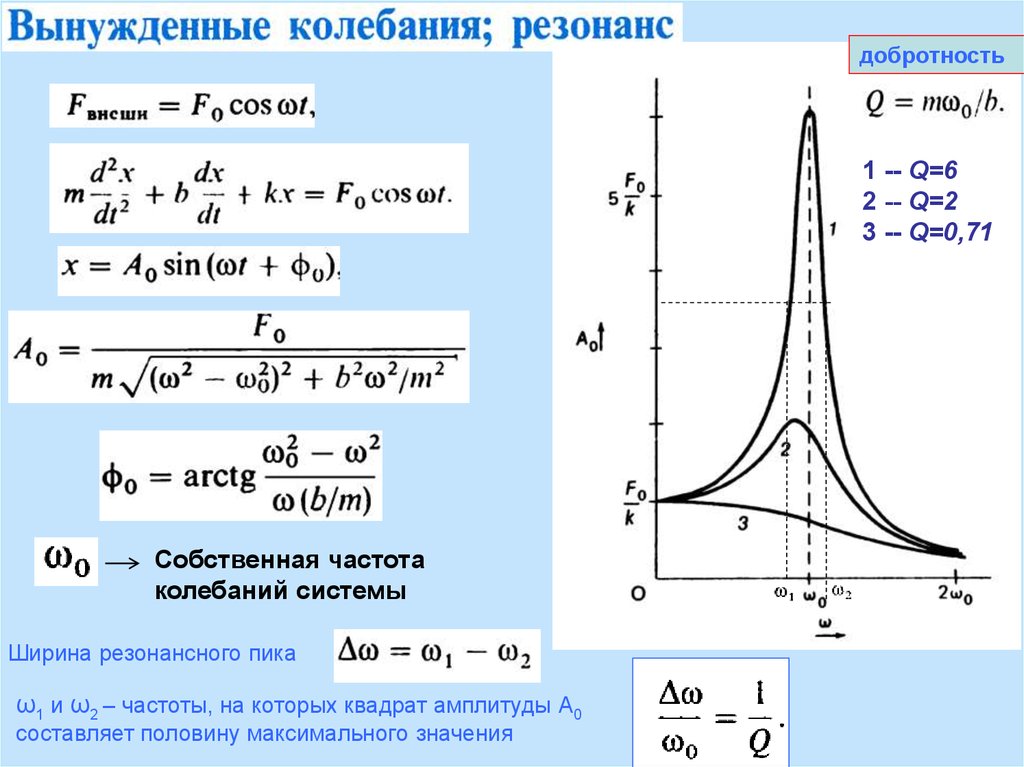
добротность
1 -- Q=6
2 -- Q=2
3 -- Q=0,71
Собственная частота
колебаний системы
Ширина резонансного пика
ω1 и ω2 – частоты, на которых квадрат амплитуды А0
составляет половину максимального значения

11.

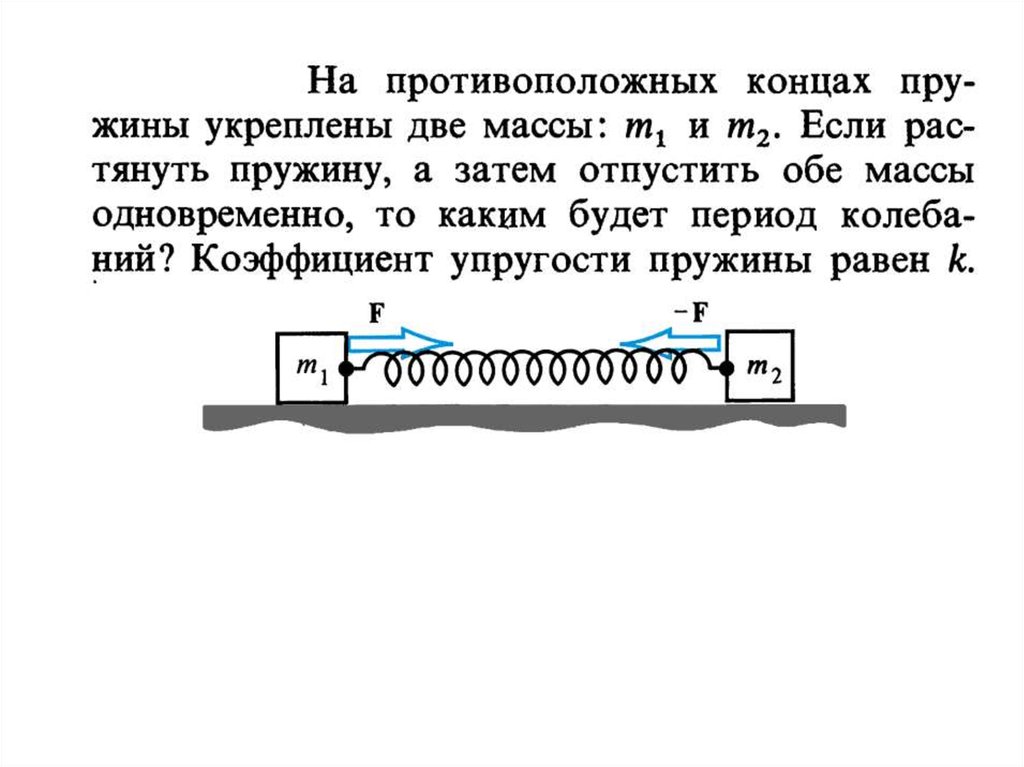
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ

12.

13.

14.

15.

16.

17.

Домашнее задание
Т
4.13, 4.28, 4.37, 4.50, 4.59, 4.61, 4.64