Похожие презентации:
Компьютерная графика. Цифровая обработка изображений, как сигналов. (Лекция 4)
1.
Компьютерная графика. Лекция 4Цифровая обработка изображений как
сигналов
2.
Цифровая обработка сигналовСигнал - это информационная функция, несущая
сообщение о физических свойствах, состоянии или
поведении какой-либо физической системы, объекта или
среды
Цели обработки сигналов:
– извлечение
определенных
информационных
сведений, которые отображены в этих сигналах
– преобразование этих сведений в форму, удобную для
восприятия и дальнейшего использования.
3.
Цифровая обработка сигналовОдномерный сигнал – это сигнал, значения которого
зависят от одной независимой переменной
– Звуковой сигнал – зависимость амплитуды
колебаний воздуха в данной точке от времени
В общем случае сигналы являются многомерными
функциями пространственных, временных и прочих
независимых переменных
Изображение – двухмерный сигнал – функция цвета от
координат
• методы обработки сигналов применимы к изображениям
так же, как и другим видам сигналов
4.
Математическое описание сигналовМатематическое описание позволяет абстрагироваться от
физической природы сигнала и материальной формы его
носителя:
– классификации сигналов, сравнение, моделирование
систем обработки сигналов
– Мат. описание сигнала - функциональной зависимость
определенного информационного параметра сигнала
от независимой переменной:
s(x), y(t) и т.п.
5.
Аналоговые сигналыЯвляются непрерывной функцией непрерывного аргумента, (определены для
любого значения аргументов)
Источники аналоговых сигналов - физические процессы, непрерывные в
динамике своего развития во времени или по другой независимой величине
Аналоговые сигналы при этом подобны («аналогичны») порождающим их
процессам
6.
Аналоговые сигналы7.
Дискретные сигналыДискретный сигнал по своим значениям – тоже непрерывная
функция, но определенная по дискретным значениям
аргумента
– Множество значений является счетным и описывается
дискретной последовательностью отсчетов (samples)
y(n*Δt)
Δt – интервал дискретизации (sampling time)
n = 0, 1, 2, …N
величина f=1/Δt – частота дискретизации (sampling
frequency, sampling rate)
8.
Дискретные сигналы9.
Пример дискретизации изображенияДискретизированное
Дискретизирование
Оригинал
Изображение (32*32)
изображение
(128*128)
10.
Цифровые сигналыЦифровой сигнал квантован по своим значениям и
дискретен по аргументу. Он описывается решетчатой
функцией yn = Qk[y(n* Δt)]
– Qk - функция квантования с числом уровней
квантования k
– Интервалы
квантования
могут
иметь
как
равномерное, так и неравномерное распределение
(напр. логарифмическое)
11.
Квантование (quantization)Квантование по уровню - процесс преобразования
бесконечных по принимаемым значениям аналоговых
отсчетов в конечное число цифровых значений
Возникающие при этом ошибки округления отсчетов
называются ошибками квантования.
12.
Пример цифрового сигнала64
цвета
Оригинал
цветов
416цвета
256
цветов
13. Как получается цифровое изображение
xy f (x)
x – характеристика яркости света
y – яркость пиксела изображения
• Свет, падая на светочувствительный элемент матрицы ПЗС
(прибор с зарядовой связью, CCD-Charge-Coupled Device),
преобразуется в электрические сигналы, зависящие от
интенсивности света проблема воссоздания цвета!
• Сигналы оцифровываются, превращаются в массив чисел
14. Причины потери качества изображения
• Ограниченный диапазона чувствительности ПЗС-матрицы• “Плохая” функция передачи ПЗС-матрицы
• “Плохая” освещенность
15.
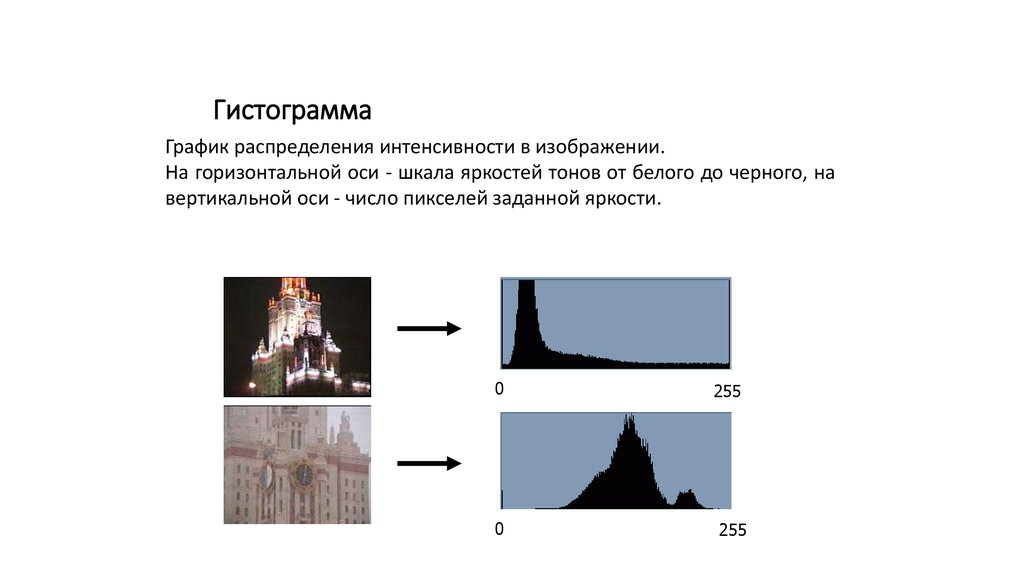
ГистограммаГрафик распределения интенсивности в изображении.
На горизонтальной оси - шкала яркостей тонов от белого до черного, на
вертикальной оси - число пикселей заданной яркости.
0
0
255
255
16.
Коррекция изображенийЧто может не устраивать в полученном изображении:
• Узкий или смещенный диапазон яркостей
(узкий диапазон - тусклое изображение, «пересвеченное»
изображение)
• Концентрация яркостей вокруг определенных значений,
неравномерное заполнение диапазона яркостей
Коррекция - к изображению применяется преобразование
яркостей, компенсирующее нежелательный эффект:
f 1 ( y) x
y – яркость пиксела на исходном изображении,
x – яркость пиксела после коррекции.
17.
Линейная коррекцияКомпенсация узкого диапазона яркостей – линейное
растяжение:
(255 0)
f ( y ) ( y ymin ) *
( ymax ymin )
1
График функции f -1(y)
18.
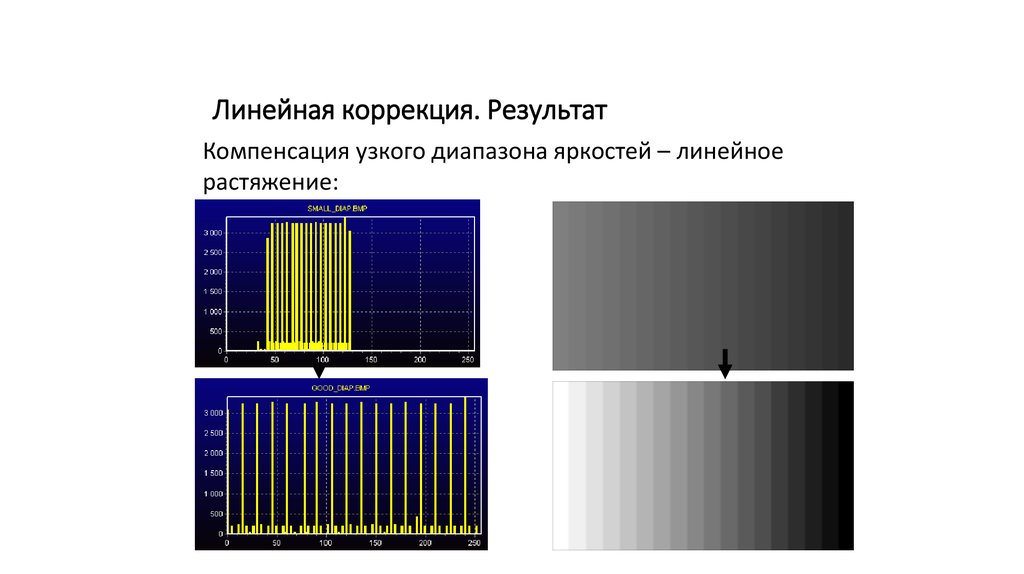
Линейная коррекция. РезультатКомпенсация узкого диапазона яркостей – линейное
растяжение:
19.
Линейная коррекция. ПримерЛинейное растяжение – «как AutoContrast в Photoshop»
20.
Линейная коррекция не всегда успешнаЛинейная коррекция не помогает, если в изображении уже
представлены все интенсивности
21.
Гамма-коррекцияГамма-коррекция (коррекция яркости монитора изменением
напряжения).
Так называют преобразование вида:
y c x
>1
<1
Графики функции f -1(y)
22.
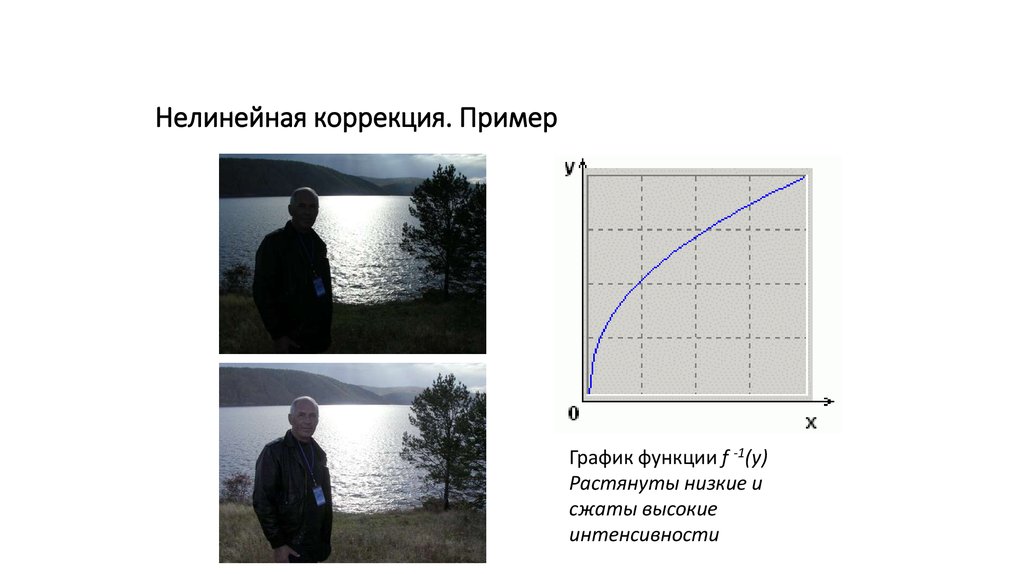
Нелинейная коррекция. ПримерГрафик функции f -1(y)
Растянуты низкие и
сжаты высокие
интенсивности
23.
Нелинейная компенсация недостаточнойконтрастности
Часто применяемые функции:
• Гамма-коррекция
Изначальная цель – коррекция для правильного
отображения на мониторе.
y c x
• Логарифмическая
Цель – сжатие динамического диапазона при визуализации
данных (связано с отображением HDR на обычные
диапазон)
y c log( 1 x)
24.
Компенсация разности освещения25.
Компенсация разности освещенияИдея:
Формирование изображения:
I (i, j ) l (i, j ) f (i, j )
Плавные изменения яркости относятся к освещению,
резкие - к объектам.
объект
f (i, j )
освещение
l (i, j )
Изображение
освещенного
объекта
I (i , j )
26.
Выравнивание освещения. АлгоритмАлгоритм
– Получить компонент освещения путем
низкочастотной фильтрации G изображения
l (i, j ) I (i, j ) G
– Восстановить изображение по формуле
I (i, j )
f (i, j )
l (i, j )
/
=
27.
Выравнивание освещения. Пример28.
Компенсация разности освещения/
=
Gauss 14.7 пикселей
29.
Цветовая коррекция изображенийИзменение цветового баланса
– Компенсация:
Неверного цветовосприятия камеры
Цветного освещения
1. Серый мир
2. Идеальный отражатель
3. Коррекция "autolevels"
4. Коррекция с опорным цветом
5. Статистическая цветокоррекция
30.
Гипотеза «Серый мир»Предположение:
Сумма всех цветов на изображении естественной сцены
дает серый цвет
Метод:
Посчитать средние яркости по всем каналам:
R
1
N
R( x, y); G
1
N
G( x, y); B
1
R G B
B
(
x
,
y
)
;
Avg
;
N
3
Масштабировать яркости пикселей по следующим
коэффициентам:
Avg
Avg
Avg
R R
; G G
; B B
;
R
G
B
31.
Гипотеза «Серый мир». Примеры32.
Гипотеза «Идеальный отражатель»Предположение:
Наиболее яркие области изображения относятся к бликам на
поверхностях, модель отражения которых такова, что цвет
блика = цвету освещения;
(дихроматическая модель)
Метод: обнаружить максимумы по каждому из каналов:
Rmax , Gmax , Bmax
Масштабировать яркости пикселов:
R*
255
;
Rmax
B*
255
;
Bmax
G*
255
;
Gmax
33.
Растяжение контрастности (“autolevels”)Идея: растянуть интенсивности по каждому из каналов на
весь диапазон;
– Метод: найти минимум, максимум по каждому из
каналов:
Rmin , Rmax , Gmin , Gmax , Bmin , Bmax
– Преобразовать интенсивности:
(255 0)
(255 0)
(255 0)
;
; ( B Bmin ) *
( R Rmin ) *
; (G Gmin ) *
( Bmax Bmin )
(Gmax Gmin )
( Rmax Rmin )
34.
Растяжение контрастности (“autolevels”)Авто
По белому
35.
Коррекция с опорным цветом– Идея: пользователь указывает целевой цвет
(например: белый, серый, черный) вручную;
Источники для указания целевого цвета:
– Знание реального цвета
– Хорошая фотография этой же сцены
Метод
– Преобразовать по каждому из каналов цвета по
формуле:
Rdst
R*
;
Rsrc
Gdst
G*
;
Gsrc
Bdst
B*
;
Bsrc
36.
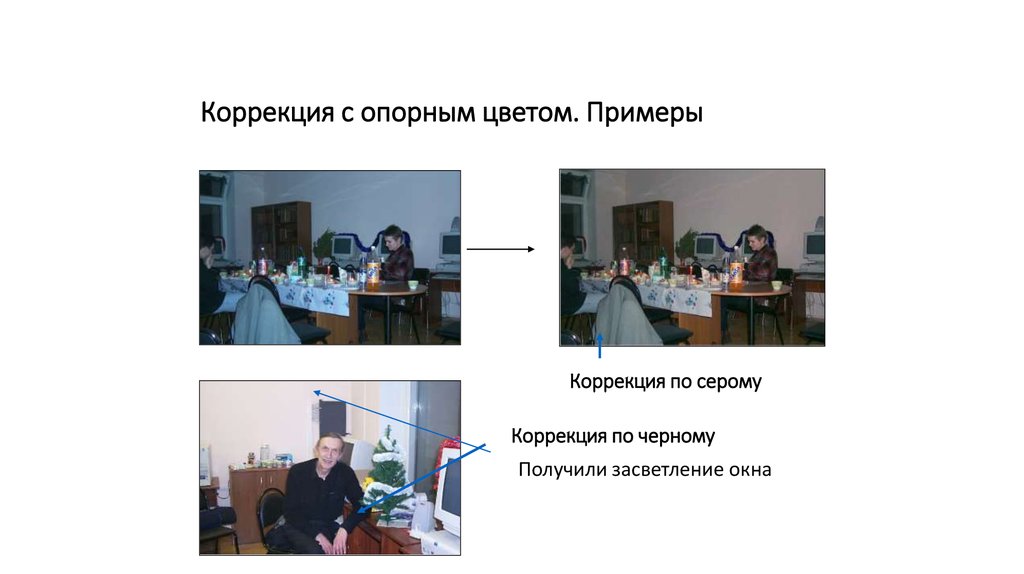
Коррекция с опорным цветом. ПримерыКоррекция по серому
Коррекция по черному
Получили засветление окна
37.
Компьютерная графика. Лекция 3В чем отличие разных фильтров
• Box filer (простое размытие) – помимо подавления шума портит резкие
границы и размывает мелкие детали изображения
• Gaussian filter – меньше размывает мелкие детали, лучше убирает шум
• Median filter – резких границ не портит, убирает мелкие детали,
изображение становится менее естественным
• Адаптивные фильтры – меньше портят детали, зависят от большего
числа параметров. Иногда изображение становится менее естественным.
• «Продвинутые» фильтры – лучшее сохранение деталей, меньше
размытие. Часто сложны в реализации и очень медленные.
38.
Компьютерная графика. Лекция 3Фильтр размытия, основанный на применении свертки
Результат
Оригинальное изображение
1
1
* 1 4 1
8
1
Ядро свертки
39.
Компьютерная графика. Лекция 3Применение свертки в компьютерной графике
Примеры фильтров:
– размытие изображений (blur);
– повышение резкости (sharpen);
– выделение контуров (edge detection);
– размытие движения (Motion blur);
– тиснение (emboss).
40.
Компьютерная графика. Лекция 3Размытие Гаусса (Gaussian Blur)
G (u , v)
1
2
2
e
( u 2 v 2 ) /( 2 2 )
41.
Компьютерная графика. Лекция 3Повышение резкости (sharpen)
1 2
1
1
2 22 2
10
1 2 1
42.
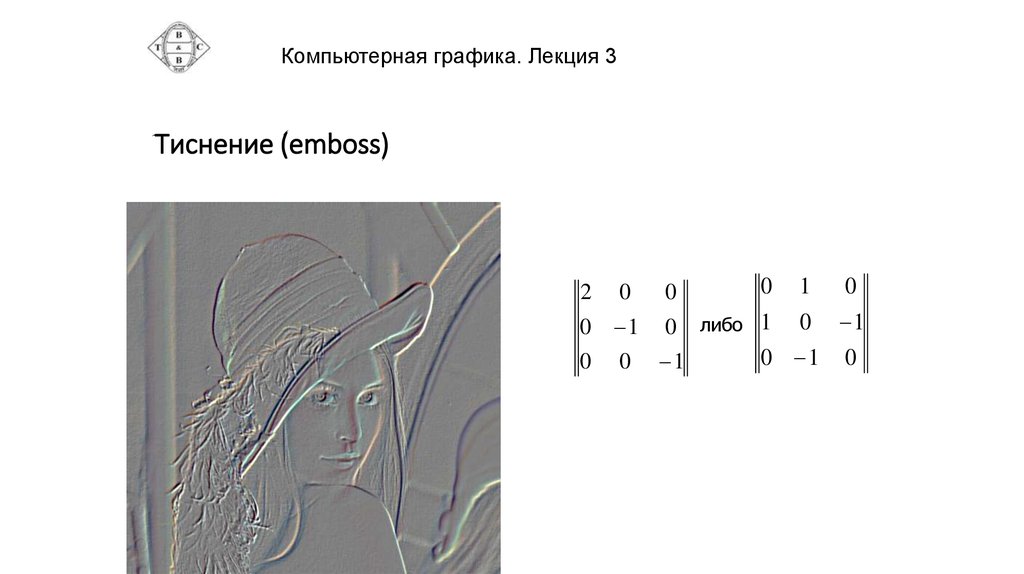
Компьютерная графика. Лекция 3Тиснение (emboss)
2
0
0
0 1
0
0
1
0
либо
0
1
0
1
0
1
0 1
0
43.
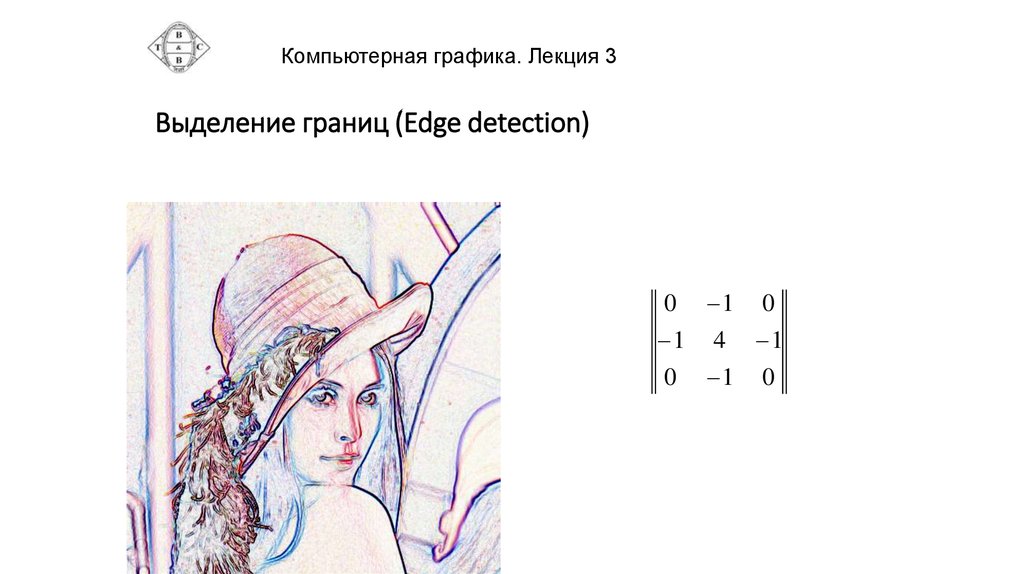
Компьютерная графика. Лекция 3Выделение границ (Edge detection)
0
1
0
1
4
1
0
1
0
44.
Компьютерная графика. Лекция 3Медианный фильтр (подавление шумов)
45.
Компьютерная графика. Лекция 3Смазывание движения (Motion Blur)
0 0 0 0 0
0 0 0 0 0
1
1 1 1 1 1
5
0 0 0 0 0
0 0 0 0 0







































 Информатика
Информатика








