Похожие презентации:
Задачи на построение
1.
05.12.2018Классная
р а б о т а.
Задачи на построение.
2.
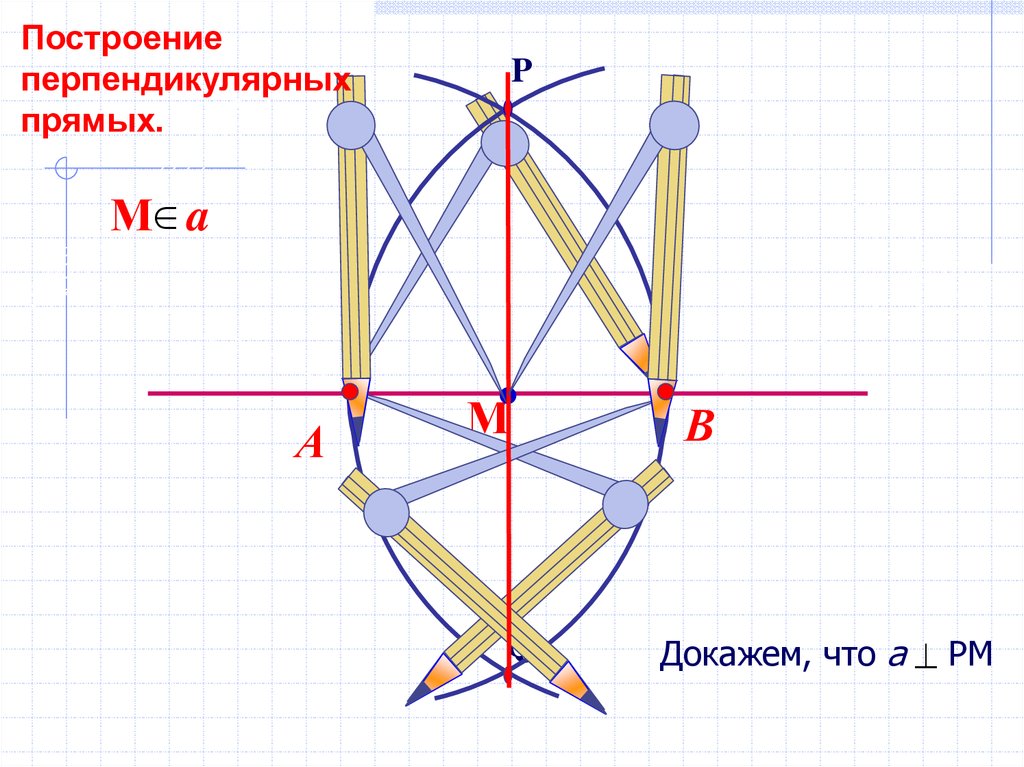
Построениеперпендикулярных
прямых.
P
М a
А
М
Q
В
Докажем, что а РМ
3.
М aP
А
М
В
a
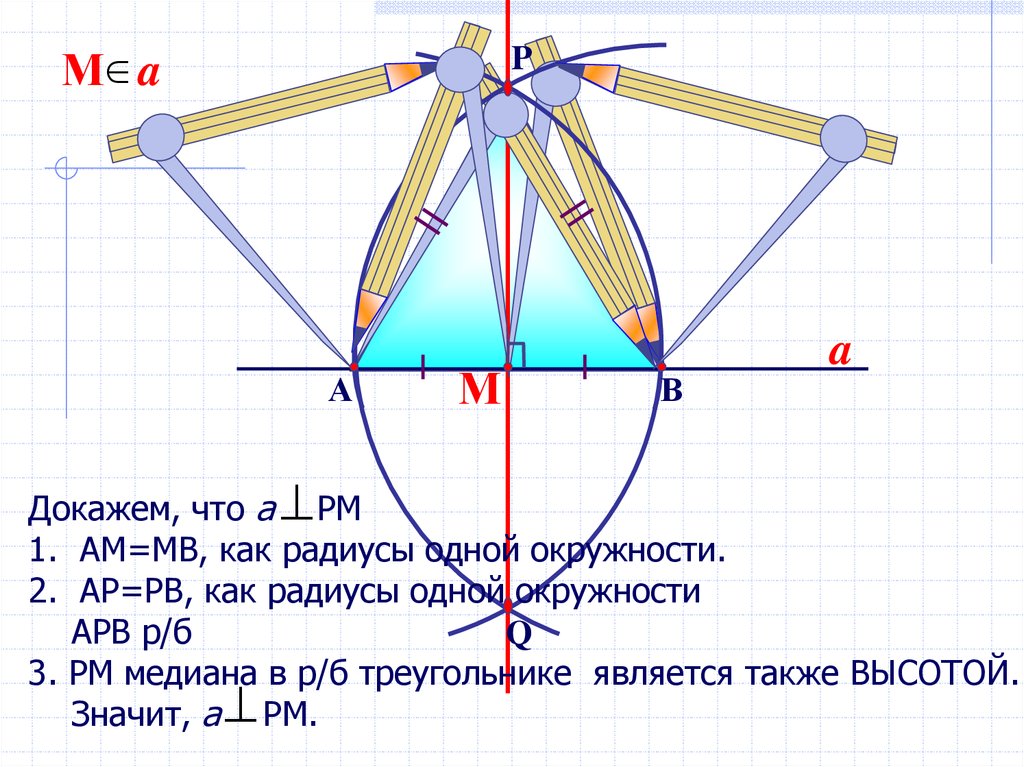
Докажем, что а РМ
1. АМ=МВ, как радиусы одной окружности.
2. АР=РВ, как радиусы одной окружности
АРВ р/б
Q
3. РМ медиана в р/б треугольнике является также ВЫСОТОЙ.
Значит, а РМ.
4.
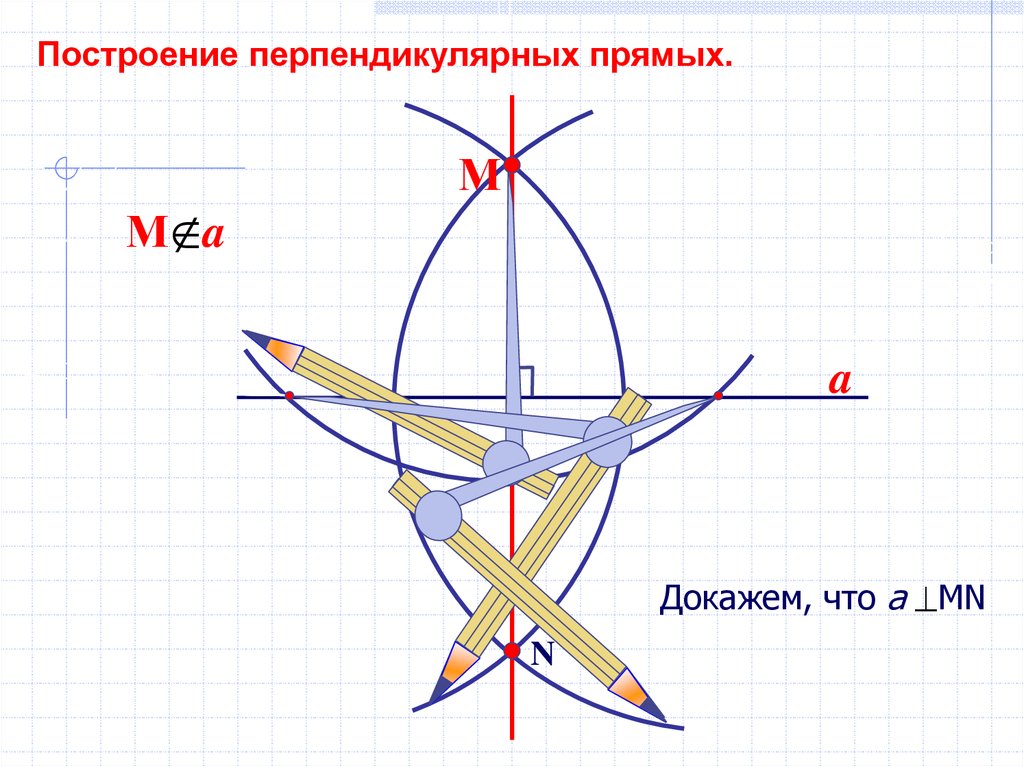
Построение перпендикулярных прямых.М a
М
a
Докажем, что а MN
N
5.
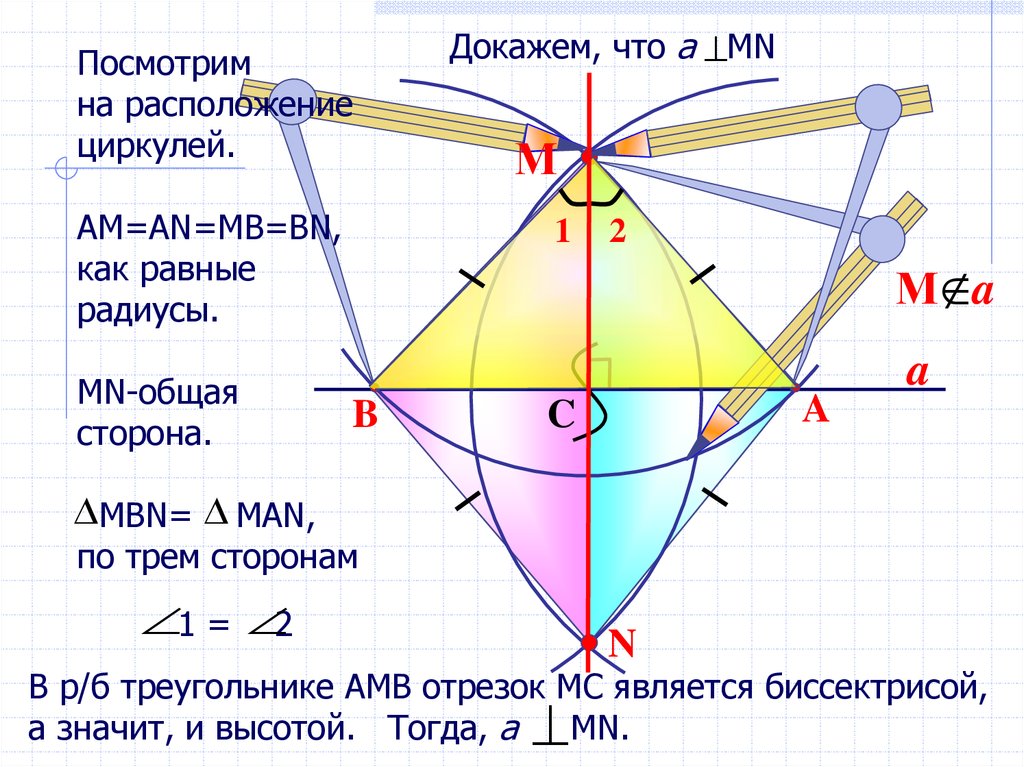
Посмотримна расположение
циркулей.
АМ=АN=MB=BN,
как равные
радиусы.
МN-общая
сторона.
Докажем, что а MN
М
1
B
2
М a
A
C
a
MВN= MAN,
по трем сторонам
1 = 2
N
В р/б треугольнике АМВ отрезок МС является биссектрисой,
а значит, и высотой. Тогда, а
МN.
6.
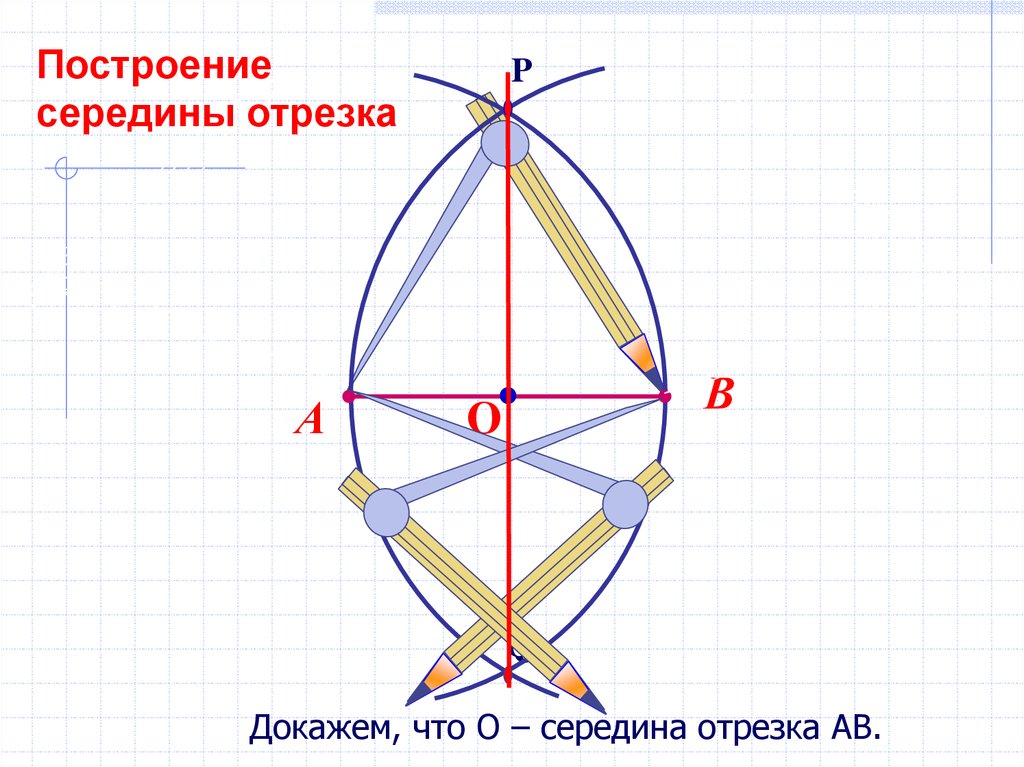
Построениесередины отрезка
А
P
В
О
Q
Докажем, что О – середина отрезка АВ.
7.
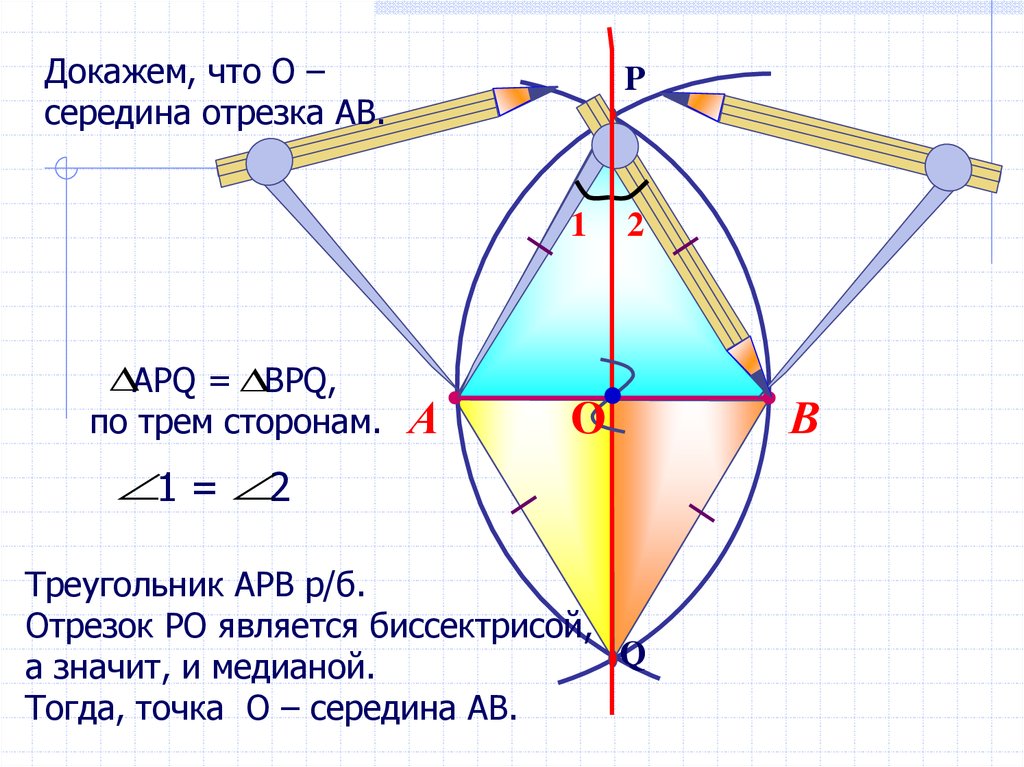
Докажем, что О –середина отрезка АВ.
P
1
АРQ = BPQ,
по трем сторонам.
А
2
О
1 = 2
Треугольник АРВ р/б.
Отрезок РО является биссектрисой,
Q
а значит, и медианой.
Тогда, точка О – середина АВ.
В
8.
п. 22-23, вопросы 20 – 21(устно,
стр.50).
Решить задачу № 154.


 Математика
Математика








