Greedy algorithms: introduction

1. Greedy Algorithms: Introduction

http://iti.wtf
Algorithms and Data Structures
Greedy Algorithms:
Introduction
Artem A. Golubnichiy
[email protected]
Department of Software of Computer Facilities and Automated Systems
Katanov Khakass State University

2. STRUCTURE OF THE CLASS

• Maximize Your Salary
• Queue of Patients
• Implementation and Analysis
• Main Ingredients
2

3. WHAT’S COMING

• Solve salary maximization problem
• Come up with a greedy algorithm yourself
• Solve optimal queue arrangement problem
• Generalize solutions using the concepts of greedy choice,
subproblem and safe choice
3

4. MAXIMIZE SALARY

4

5. MAXIMIZE SALARY

5

6. MAXIMIZE SALARY

6

7. LARGEST NUMBER

Toy problem
What is the largest number that consists of digits 9, 8, 9, 6, 1? Use
all the digits.
7

8. LARGEST NUMBER

Toy problem
What is the largest number that consists of digits 9, 8, 9, 6, 1? Use
all the digits.
Examples
16899, 69891, 98961, . . .
8

9. LARGEST NUMBER

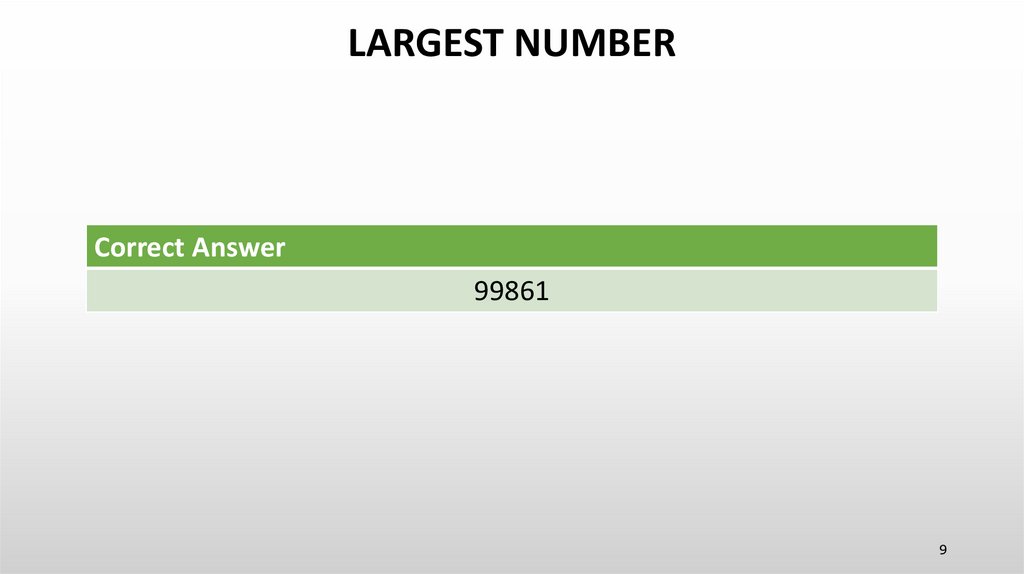
Correct Answer
99861
9

10. GREEDY STRATEGY

{9, 8, 9, 6, 1}
→
? ? ? ? ?
10

11. GREEDY STRATEGY

Find max
{9, 8, 9, 6, 1}
Find max digit
11

12. GREEDY STRATEGY

Find max
{9, 8, 9, 6, 1}
Find max digit
12

13. GREEDY STRATEGY

Find max
{9, 8, 9, 6, 1}
Append
→
Find max digit
Append it to the number
13

14. GREEDY STRATEGY

Find max
{9, 8, 9, 6, 1}
Append
→
9
Find max digit
Append it to the number
14

15. GREEDY STRATEGY

Find max
{9, 8, 9, 6, 1}
Append
→
9
Remove
Find max digit
Append it to the number
Remove it from the list of digits
15

16. GREEDY STRATEGY

Find max
{9, 8, 9, 6, 1}
Append
→
9
Remove
Find max digit
Append it to the number
Remove it from the list of digits
16

17. GREEDY STRATEGY

Find max
{8, 9, 6, 1}
Append
→
9
Remove
Find max digit
Append it to the number
Remove it from the list of digits
Repeat while there are digits in the list
17

18. GREEDY STRATEGY

Find max
{8, 9, 6, 1}
Append
→
9
Remove
Find max digit
Append it to the number
Remove it from the list of digits
Repeat while there are digits in the list
18

19. GREEDY STRATEGY

Find max
{8, 9, 6, 1}
Append
→
99
Remove
Find max digit
Append it to the number
Remove it from the list of digits
Repeat while there are digits in the list
19

20. GREEDY STRATEGY

Find max
{8, 9, 6, 1}
Append
→
99
Remove
Find max digit
Append it to the number
Remove it from the list of digits
Repeat while there are digits in the list
20

21. GREEDY STRATEGY

Find max
{8, 6, 1}
Append
→
99
Remove
Find max digit
Append it to the number
Remove it from the list of digits
Repeat while there are digits in the list
21

22. GREEDY STRATEGY

Find max
{8, 6, 1}
Append
→
99
Remove
Find max digit
Append it to the number
Remove it from the list of digits
Repeat while there are digits in the list
22

23. GREEDY STRATEGY

Find max
{8, 6, 1}
Append
→
998
Remove
Find max digit
Append it to the number
Remove it from the list of digits
Repeat while there are digits in the list
23

24. GREEDY STRATEGY

Find max
{8, 6, 1}
Append
→
998
Remove
Find max digit
Append it to the number
Remove it from the list of digits
Repeat while there are digits in the list
24

25. GREEDY STRATEGY

Find max
{6, 1}
Append
→
998
Remove
Find max digit
Append it to the number
Remove it from the list of digits
Repeat while there are digits in the list
25

26. GREEDY STRATEGY

Find max
{6, 1}
Append
→
998
Remove
Find max digit
Append it to the number
Remove it from the list of digits
Repeat while there are digits in the list
26

27. GREEDY STRATEGY

Find max
{6, 1}
Append
→
9986
Remove
Find max digit
Append it to the number
Remove it from the list of digits
Repeat while there are digits in the list
27

28. GREEDY STRATEGY

Find max
{6, 1}
Append
→
9986
Remove
Find max digit
Append it to the number
Remove it from the list of digits
Repeat while there are digits in the list
28

29. GREEDY STRATEGY

Find max
{1}
→
Append
9986
Remove
Find max digit
Append it to the number
Remove it from the list of digits
Repeat while there are digits in the list
29

30. GREEDY STRATEGY

Find max
{1}
→
Append
9986
Remove
Find max digit
Append it to the number
Remove it from the list of digits
Repeat while there are digits in the list
30

31. GREEDY STRATEGY

Find max
{1}
→
Append
99861
Remove
Find max digit
Append it to the number
Remove it from the list of digits
Repeat while there are digits in the list
31

32. GREEDY STRATEGY

Find max
{1}
→
Append
99861
Remove
Find max digit
Append it to the number
Remove it from the list of digits
Repeat while there are digits in the list
32

33. GREEDY STRATEGY

Find max
{}
→
Append
99861
Remove
Find max digit
Append it to the number
Remove it from the list of digits
Repeat while there are digits in the list
33

34. GREEDY STRATEGY

Find max
{9, 8, 9, 6, 1}
Append
→
Remove
99861
Success!
Find max digit
Append it to the number
Remove it from the list of digits
Repeat while there are digits in the list
34

35. QUEUE OF PATIENTS

35

36. QUEUE OF PATIENTS

Queue Arrangement
Input:
n patients have come to the doctor’s office at 9:00AM. They
can be treated in any order. For i-th patient, the time needed
for treatment is ti. You need to arrange the patients in such a
queue that the total waiting time is minimized.
Output: The minimum total waiting time.
36

37. QUEUE OF PATIENTS

Optimal Queue Arrangement
t1 =15, t2 =20 and t3 =10. Arrangement (1, 2, 3):
• First patient doesn’t wait
37

38. QUEUE OF PATIENTS

Optimal Queue Arrangement
t1 =15, t2 =20 and t3 =10. Arrangement (1, 2, 3):
• First patient doesn’t wait
• Second patient waits for 15 minutes
38

39. QUEUE OF PATIENTS

Optimal Queue Arrangement
t1 =15, t2 =20 and t3 =10. Arrangement (1, 2, 3):
• First patient doesn’t wait
• Second patient waits for 15 minutes
• Third patient waits for 15 + 20 = 35 minutes
39

40. QUEUE OF PATIENTS

Optimal Queue Arrangement
t1 =15, t2 =20 and t3 =10. Arrangement (1, 2, 3):
• First patient doesn’t wait
• Second patient waits for 15 minutes
• Third patient waits for 15 + 20 = 35 minutes
• Total waiting time 15 + 35 = 50 minutes
40

41. QUEUE OF PATIENTS

Optimal Queue Arrangement
t1 =15, t2 =20 and t3 =10. Arrangement (3, 1, 2):
• First patient doesn’t wait
41

42. QUEUE OF PATIENTS

Optimal Queue Arrangement
t1 =15, t2 =20 and t3 =10. Arrangement (3, 1, 2):
• First patient doesn’t wait
• Second patient waits for 10 minutes
42

43. QUEUE OF PATIENTS

Optimal Queue Arrangement
t1 =15, t2 =20 and t3 =10. Arrangement (3, 1, 2):
• First patient doesn’t wait
• Second patient waits for 10 minutes
• Third patient waits for 10 + 15 = 25 minutes
43

44. QUEUE OF PATIENTS

Optimal Queue Arrangement
t1 =15, t2 =20 and t3 =10. Arrangement (3, 1, 2):
• First patient doesn’t wait
• Second patient waits for 10 minutes
• Third patient waits for 10 + 15 = 25 minutes
• Total waiting time 10 + 25 = 35 minutes
44

45. GREEDY STRATEGY

• Make some greedy choice
• Reduce to a smaller problem
• Iterate
45

46. GREEDY CHOICE

• First treat the patient with the maximum treatment time
• First treat the patient with the minimum treatment time
• First treat the patient with average treatment time
46

47. GREEDY ALGORITHM

• First treat the patient with the minimum treatment time
47

48. GREEDY ALGORITHM

• First treat the patient with the minimum treatment time
• Remove this patient from the queue
48

49. GREEDY ALGORITHM

• First treat the patient with the minimum treatment time
• Remove this patient from the queue
• Treat all the remaining patients in such order as to minimize their total
waiting time
49

50. SUBPROBLEM

Definition
Subproblem is a similar problem of smaller size.
50

51. SUBPROBLEM

Examples
• MaximumSalary(1, 9, 8, 9, 6) =
51

52. SUBPROBLEM

Examples
• MaximumSalary(1, 9, 8, 9, 6) =
‘‘9’’ + MaximumSalary(1, 8, 9, 6)
52

53. SUBPROBLEM

Examples
• MaximumSalary(1, 9, 8, 9, 6) =
‘‘9’’ + MaximumSalary(1, 8, 9, 6)
• Minimum total waiting time for n patients = (n − 1) · tmin+
53

54. SUBPROBLEM

Examples
• MaximumSalary(1, 9, 8, 9, 6) =
‘‘9’’ + MaximumSalary(1, 8, 9, 6)
• Minimum total waiting time for n patients = (n − 1) · tmin+ minimum
total waiting time for n − 1 patients without tmin
54

55. SAFE CHOICE

Definition
A greedy choice is called safe choice if there is an optimal solution
consistent with this first choice.
55

56. SAFE CHOICE

Lemma
To treat the patient with minimum treatment time tmin first is a safe
choice.
56

57. PROOF IDEA

• Is it possible for an optimal arrangement to have two consecutive patients in
order with treatment times t1 and t2 such that t1 > t2?
57

58. PROOF IDEA

• Is it possible for an optimal arrangement to have two consecutive patients in
order with treatment times t1 and t2 such that t1 > t2?
• It is impossible. Assume there is such an optimal arrangement and consider
what happens if we swap these two patients.
58

59. PROOF IDEA

• Is it possible for an optimal arrangement to have two consecutive patients in
order with treatment times t1 and t2 such that t1 > t2?
• It is impossible. Assume there is such an optimal arrangement and consider
what happens if we swap these two patients.
• If we swap two consecutive patients with treatment times t1 > t2: Waiting
time for all the patients before and after these two doesn’t change
59

60. PROOF IDEA

• Is it possible for an optimal arrangement to have two consecutive patients in
order with treatment times t1 and t2 such that t1 > t2?
• It is impossible. Assume there is such an optimal arrangement and consider
what happens if we swap these two patients.
• If we swap two consecutive patients with treatment times t1 > t2: Waiting
time for all the patients before and after these two doesn’t change
• Waiting time for the patient which was first increases by t2, and for the
second one it decreases by t1
60

61. PROOF IDEA

• Is it possible for an optimal arrangement to have two consecutive patients in
order with treatment times t1 and t2 such that t1 > t2?
• It is impossible. Assume there is such an optimal arrangement and consider
what happens if we swap these two patients.
• If we swap two consecutive patients with treatment times t1 > t2: Waiting
time for all the patients before and after these two doesn’t change
• Waiting time for the patient which was first increases by t2, and for the
second one it decreases by t1
• Total waiting time increases by t2 − t1 < 0, so it actually decreases
61

62. PROOF IDEA

We have just proved:
Lemma
In any optimal arrangement of the patients, first of any two consecutive
patients has smaller treatment time.
62

63. SAFE CHOICE PROOF

• Assume the patient with treatment time tmin is not the first
63

64. SAFE CHOICE PROOF

• Assume the patient with treatment time tmin is not the first
• Let i > 1 be the position of the first patient with treatment time tmin in the
optimal arrangement
64

65. SAFE CHOICE PROOF

• Assume the patient with treatment time tmin is not the first
• Let i > 1 be the position of the first patient with treatment time tmin in the
optimal arrangement
• Then the patient at position i − 1 has bigger treatment time — a
contradiction
65

66. Conclusion

Now we know that the following greedy algorithm works correctly:
• First treat the patient with the minimum treatment time
66

67. Conclusion

Now we know that the following greedy algorithm works correctly:
• First treat the patient with the minimum treatment time
• Remove this patient from the queue
67

68. Conclusion

Now we know that the following greedy algorithm works correctly:
• First treat the patient with the minimum treatment time
• Remove this patient from the queue
• Treat all the remaining patients in such order as to minimize their total
waiting time
68

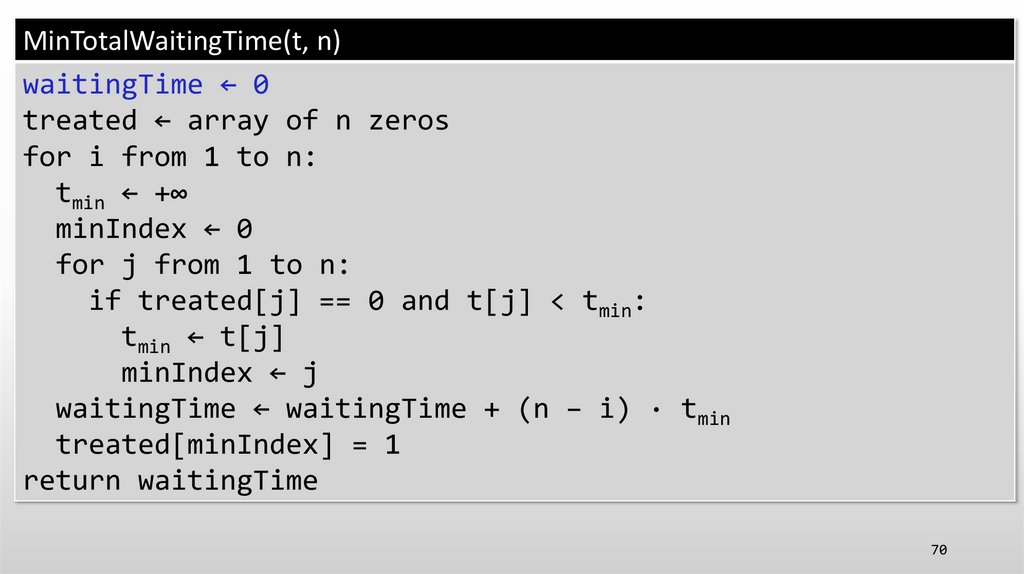
69.

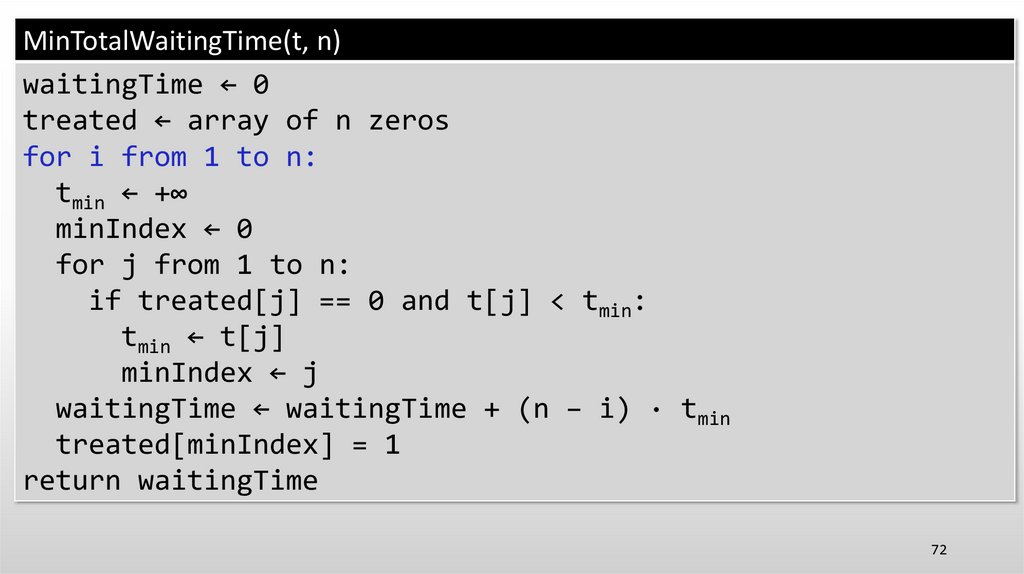
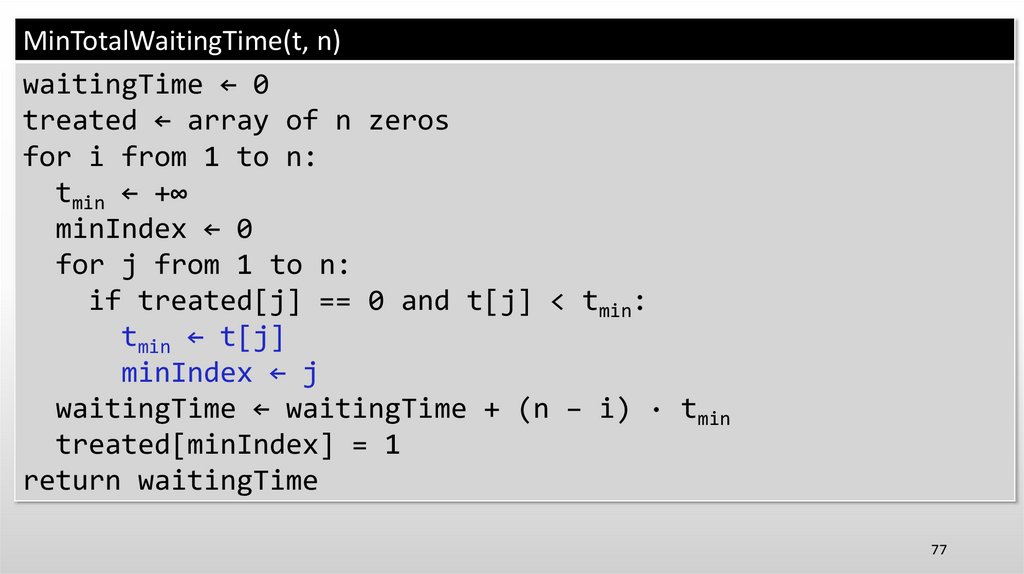
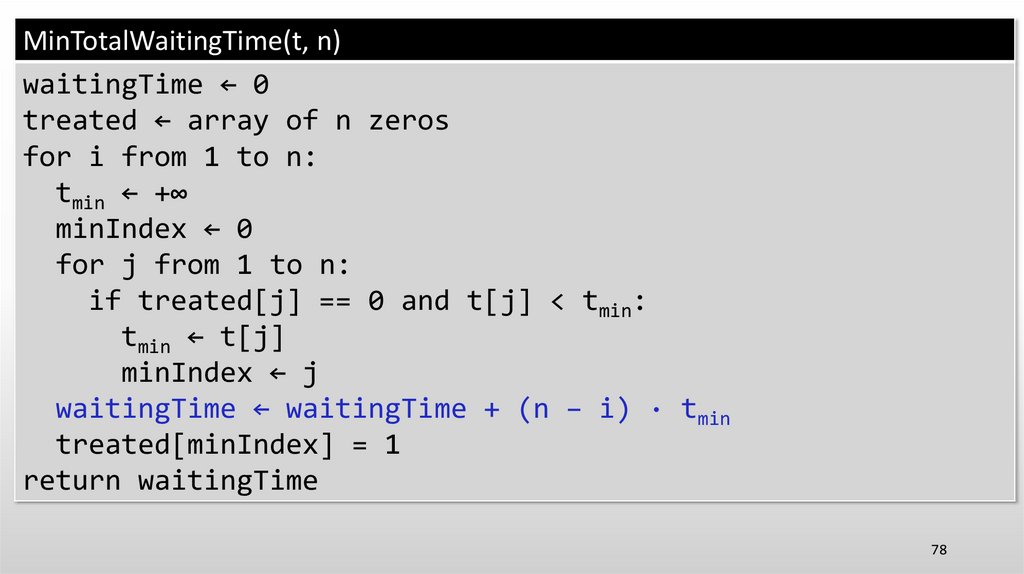
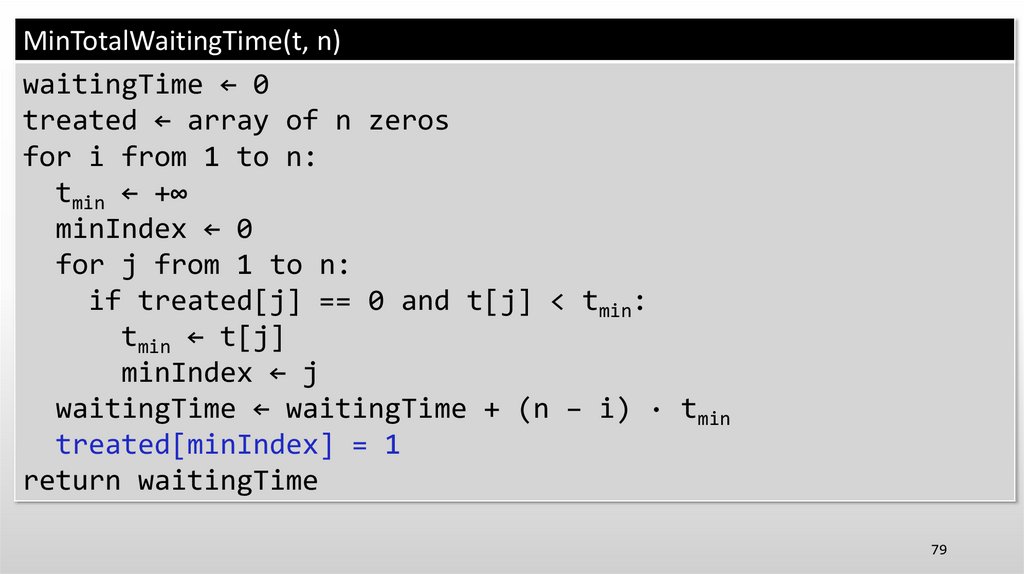
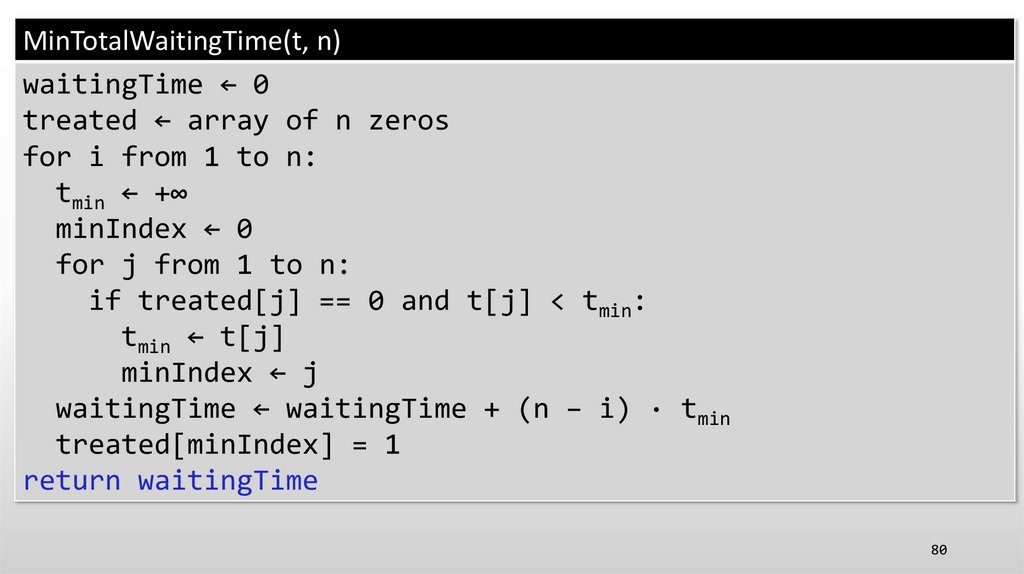
MinTotalWaitingTime(t, n)
waitingTime ← 0
treated ← array of n zeros
for i from 1 to n:
tmin ← +∞
minIndex ← 0
for j from 1 to n:
if treated[j] == 0 and t[j] < tmin:
tmin ← t[j]
minIndex ← j
waitingTime ← waitingTime + (n − i) · tmin
treated[minIndex] = 1
return waitingTime
69

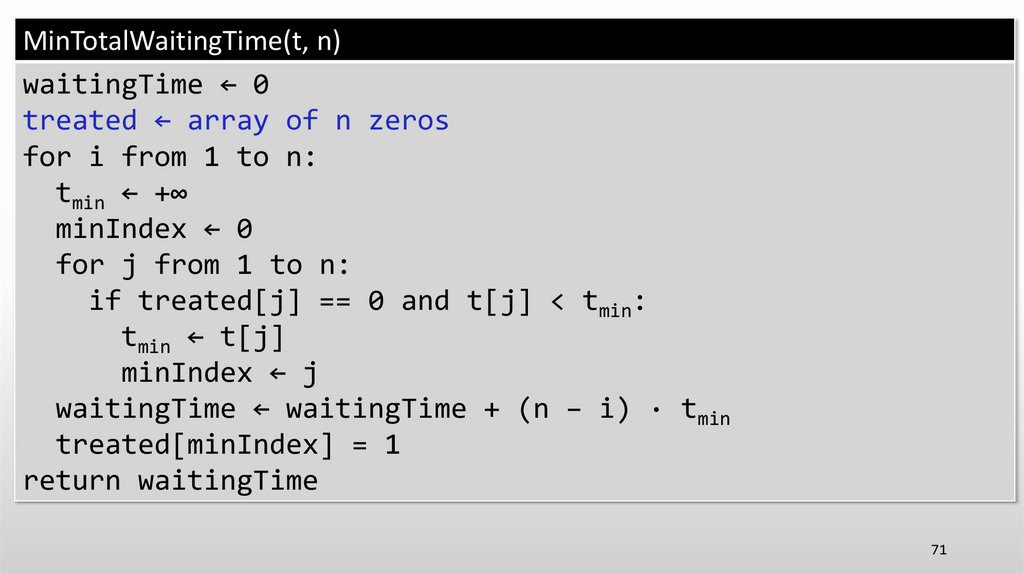
70.

MinTotalWaitingTime(t, n)
waitingTime ← 0
treated ← array of n zeros
for i from 1 to n:
tmin ← +∞
minIndex ← 0
for j from 1 to n:
if treated[j] == 0 and t[j] < tmin:
tmin ← t[j]
minIndex ← j
waitingTime ← waitingTime + (n − i) · tmin
treated[minIndex] = 1
return waitingTime
70

71.

MinTotalWaitingTime(t, n)
waitingTime ← 0
treated ← array of n zeros
for i from 1 to n:
tmin ← +∞
minIndex ← 0
for j from 1 to n:
if treated[j] == 0 and t[j] < tmin:
tmin ← t[j]
minIndex ← j
waitingTime ← waitingTime + (n − i) · tmin
treated[minIndex] = 1
return waitingTime
71

72.

MinTotalWaitingTime(t, n)
waitingTime ← 0
treated ← array of n zeros
for i from 1 to n:
tmin ← +∞
minIndex ← 0
for j from 1 to n:
if treated[j] == 0 and t[j] < tmin:
tmin ← t[j]
minIndex ← j
waitingTime ← waitingTime + (n − i) · tmin
treated[minIndex] = 1
return waitingTime
72

73.

MinTotalWaitingTime(t, n)
waitingTime ← 0
treated ← array of n zeros
for i from 1 to n:
tmin ← +∞
minIndex ← 0
for j from 1 to n:
if treated[j] == 0 and t[j] < tmin:
tmin ← t[j]
minIndex ← j
waitingTime ← waitingTime + (n − i) · tmin
treated[minIndex] = 1
return waitingTime
73

74.

MinTotalWaitingTime(t, n)
waitingTime ← 0
treated ← array of n zeros
for i from 1 to n:
tmin ← +∞
minIndex ← 0
for j from 1 to n:
if treated[j] == 0 and t[j] < tmin:
tmin ← t[j]
minIndex ← j
waitingTime ← waitingTime + (n − i) · tmin
treated[minIndex] = 1
return waitingTime
74

75.

MinTotalWaitingTime(t, n)
waitingTime ← 0
treated ← array of n zeros
for i from 1 to n:
tmin ← +∞
minIndex ← 0
for j from 1 to n:
if treated[j] == 0 and t[j] < tmin:
tmin ← t[j]
minIndex ← j
waitingTime ← waitingTime + (n − i) · tmin
treated[minIndex] = 1
return waitingTime
75

76.

MinTotalWaitingTime(t, n)
waitingTime ← 0
treated ← array of n zeros
for i from 1 to n:
tmin ← +∞
minIndex ← 0
for j from 1 to n:
if treated[j] == 0 and t[j] < tmin:
tmin ← t[j]
minIndex ← j
waitingTime ← waitingTime + (n − i) · tmin
treated[minIndex] = 1
return waitingTime
76

77.

MinTotalWaitingTime(t, n)
waitingTime ← 0
treated ← array of n zeros
for i from 1 to n:
tmin ← +∞
minIndex ← 0
for j from 1 to n:
if treated[j] == 0 and t[j] < tmin:
tmin ← t[j]
minIndex ← j
waitingTime ← waitingTime + (n − i) · tmin
treated[minIndex] = 1
return waitingTime
77

78.

MinTotalWaitingTime(t, n)
waitingTime ← 0
treated ← array of n zeros
for i from 1 to n:
tmin ← +∞
minIndex ← 0
for j from 1 to n:
if treated[j] == 0 and t[j] < tmin:
tmin ← t[j]
minIndex ← j
waitingTime ← waitingTime + (n − i) · tmin
treated[minIndex] = 1
return waitingTime
78

79.

MinTotalWaitingTime(t, n)
waitingTime ← 0
treated ← array of n zeros
for i from 1 to n:
tmin ← +∞
minIndex ← 0
for j from 1 to n:
if treated[j] == 0 and t[j] < tmin:
tmin ← t[j]
minIndex ← j
waitingTime ← waitingTime + (n − i) · tmin
treated[minIndex] = 1
return waitingTime
79

80.

MinTotalWaitingTime(t, n)
waitingTime ← 0
treated ← array of n zeros
for i from 1 to n:
tmin ← +∞
minIndex ← 0
for j from 1 to n:
if treated[j] == 0 and t[j] < tmin:
tmin ← t[j]
minIndex ← j
waitingTime ← waitingTime + (n − i) · tmin
treated[minIndex] = 1
return waitingTime
80

81.

Lemma
The running time of MinTotalWaitingTime(t, n) is O(n2).
81

82.

Lemma
The running time of MinTotalWaitingTime(t, n) is O(n2).
Proof
• i changes from 1 to n
82

83.

Lemma
The running time of MinTotalWaitingTime(t, n) is O(n2).
Proof
• i changes from 1 to n
• For each value of i, j changes from 1 to n
83

84.

Lemma
The running time of MinTotalWaitingTime(t, n) is O(n2).
Proof
• i changes from 1 to n
• For each value of i, j changes from 1 to n
• This results in O(n2)
84

85.

• Actually, this problem can be solved in time O(n log n)
85

86.

• Actually, this problem can be solved in time O(n log n)
• Instead of choosing the patient with minimum treatment time
out of remaining ones n times, sort patients by increasing
treatment time
86

87.

• Actually, this problem can be solved in time O(n log n)
• Instead of choosing the patient with minimum treatment time
out of remaining ones n times, sort patients by increasing
treatment time
• This sorted arrangement is optimal
87

88.

• Actually, this problem can be solved in time O(n log n)
• Instead of choosing the patient with minimum treatment time
out of remaining ones n times, sort patients by increasing
treatment time
• This sorted arrangement is optimal
• It is possible to sort n patients in time O(n log n)
88

89.

REDUCTION TO SUBPROBLEM
• Make some first choice
• Then solve a problem of the same kind
• Smaller: fewer digits, fewer patients
• This is called a “subproblem”
89

90.

SAFE CHOICE
• A choice is called safe if there is an optimal solution consistent with
this first choice
90

91.

SAFE CHOICE
• A choice is called safe if there is an optimal solution consistent with
this first choice
• Not all first choices are safe
91

92.

SAFE CHOICE
• A choice is called safe if there is an optimal solution consistent with
this first choice
• Not all first choices are safe
• Greedy choices are often unsafe
92

93.

GENERAL STRATEGY
Problem
93

94.

GENERAL STRATEGY
greedy choice
Problem
Make a greedy choice
94

95.

GENERAL STRATEGY
greedy choice
Problem
Make a greedy choice
Prove that it is a safe choice
Safe choice
95

96.

GENERAL STRATEGY
greedy choice
Problem
Safe choice
Subproblem
Make a greedy choice
Prove that it is a safe choice
Reduce to a subproblem
96

97.

GENERAL STRATEGY
greedy choice
Problem
Safe choice
Subproblem
Make a greedy choice
Prove that it is a safe choice
Reduce to a subproblem
Solve the subproblem
97