Похожие презентации:
Neural networks
1. Kazan National Research Technical University named after A.N. Tupolev German-Russian Institute of Advanced Technologies (GRIAT)
NEURAL NETWORKSby Dr. Igor Anikin
2. Table of contents
The basic concepts of neural networksSingle layer neural networks
Artificial neural networks.
The structure of an artificial neuron.
Activation functions.
Basic paradigms of neural networks.
Fundamentals of learning and training samples.
Using neural networks in practice
Rosenblatt's single layer perceptron.
Learning single layer neural networks.
Associative memory and its realization on single layer neural networks.
Using single layer neural networks for pattern recognition and time
series forecasing.
Multilayer perceptrons
The structure of multilayer perceptrons
Back propagation of error.
Using multilayer perceptrons for pattern recognition and time series
forecasing.
3.
Self-organizing mapsThe principle of unsupervised learning.
Kohonen self-organizing maps.
Learning Kohonen networks.
Practical using of Kohonen networks
Recurent neural networks
Neural networks with feedback.
Hopfield neural network.
Hamming neural network.
Training Hopfield and Hamming neural networks.
Practical using of Hopfield and Hamming neural networks.
Training and Testing
Training error and testing error.
4. References
1.2.
3.
4.
David Kriesel.
Neural
A
brief Introduction
networks
to
//
http://www.dkriesel.com/en/science/neural_net
works
Raul Rojas. Neural Networks. A Systematic
Introduction
//
http://www.inf.fu-berlin.de/inst/ag-ki/rojas_
home/documents/1996/NeuralNetworks/neuron.pdf
.
L.P.J. Veelenturf. Analysis and Application of
Artificial
Neural
Networks
//
http://www.ru.lv/~peter/zinatne/ebooks/Anal
ysis%20and%20Applications%20of%20Artificial
%20Neural%20Networks.pdf
Artificial Neural Networks – Methodological
Advances and Biomedical Applications //
5.
The basic concepts ofneural networks
6. Questions for motivation discussion
What tasks are machines good at doing thathumans are not?
What tasks are humans good at doing that
machines are not?
What tasks are both good at?
What does it mean to learn?
How is learning related to intelligence?
What does it mean to be intelligent?
Do you believe a machine will ever been
intelligent?
If a computer were intelligent, how would
you know?
7. Types of learning
Knowledge acquisition from expert.Knowledge acquisition from data:
Supervised learning – the system is supplied
with a set of training examples consisting of
inputs and corresponding outputs, and is
required to discover the relation or mapping
between them.
Unsupervised learning – the system is
supplied with a set of training examples
consisting only of inputs. It is required to
discover what appropriate outputs should be.
8. Artificial Neural Network
An extremely simplified model of thehuman’s brain
Transforms inputs into the best outputs
(some neural networks are the universal
function approximators).
9. Artificial Neural Networks
Development of Neural Networks date back to the early1940s.
It experienced an upsurge in popularity in the late 1980s
due to discovery of new techniques of NN training.
Some NNs are models of biological neural networks and
some are not, but historically, much of the inspiration for the
field of NNs came from the desire to produce artificial
systems capable of sophisticated, perhaps intelligent,
computations similar to those that the human brain
routinely performs, and thereby possibly to enhance our
understanding of the human brain.
Most NNs have some sort of training rule. In other words,
NNs learn from the examples (as children learn to recognize
dogs from examples of dogs) and exhibit some capability for
generalization beyond the training data.
10. ANN vs Computers
Computershave
programmed
to
be
explicitly
Analyze the problem to be solved.
Write the code in a programming language.
Neural networks learn from the examples
No requirement of an explicit description of the problem.
No need for a programmer.
The neural computer adapts itself during a training
period, based on examples of similar problems even
without a desired solution to each problem. After
sufficient training the neural computer is able to relate
the problem data to the solutions, inputs to outputs, and
it is then able to offer a viable solution to a brand new
problem.
11. ANN vs Computers
Digital ComputersDeductive Reasoning. We
apply known rules to input
data to produce output.
Computation
is
centralized, synchronous,
and serial.
Memory is literally stored,
and location addressable.
Not fault tolerant. One
transistor goes and it no
longer works.
Exact.
Static connectivity.
Applicable if well-defined
rules
accessible
with
precise input data.
Neural Networks
Inductive
Reasoning. We use
given input and output data
(training examples) to make a
reasoning.
Computation
is
collective,
asynchronous, and parallel.
Memory
is
distributed,
internalized, short term and
content addressable.
Fault tolerant, redundancy, and
sharing of responsibilities.
Inexact.
Dynamic connectivity.
Applicable if rules are unknown
or complicated, or if data are
noisy or partial.
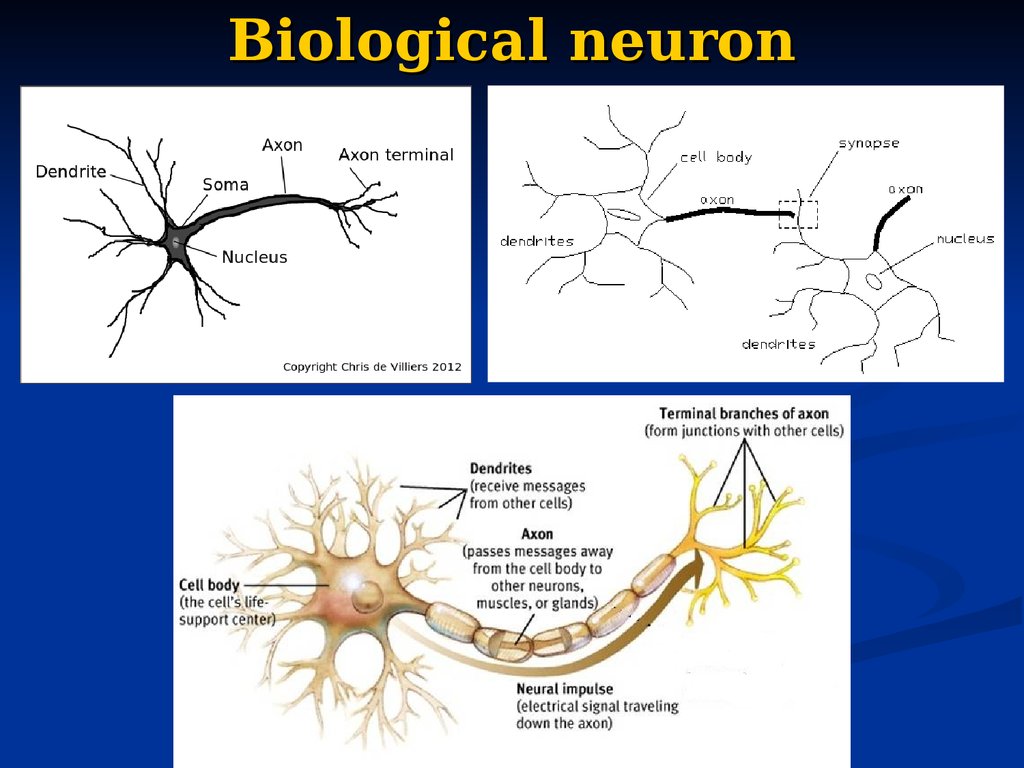
12. Biological neuron
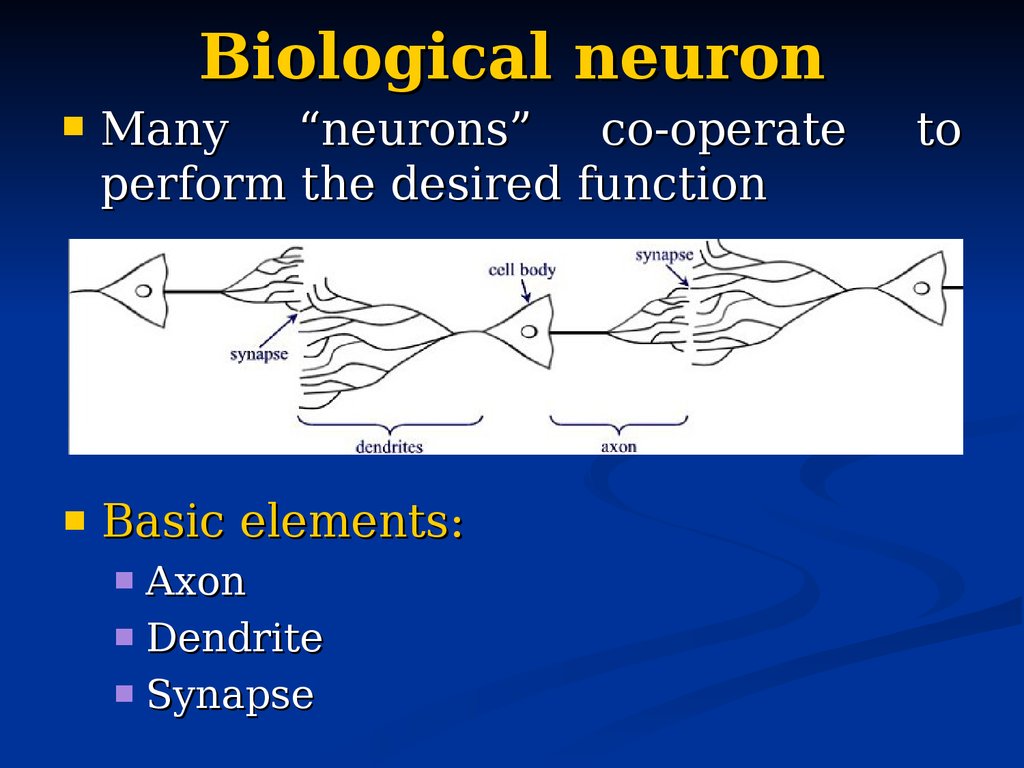
13. Biological neuron
Many“neurons”
co-operate
perform the desired function
Basic elements:
Axon
Dendrite
Synapse
to
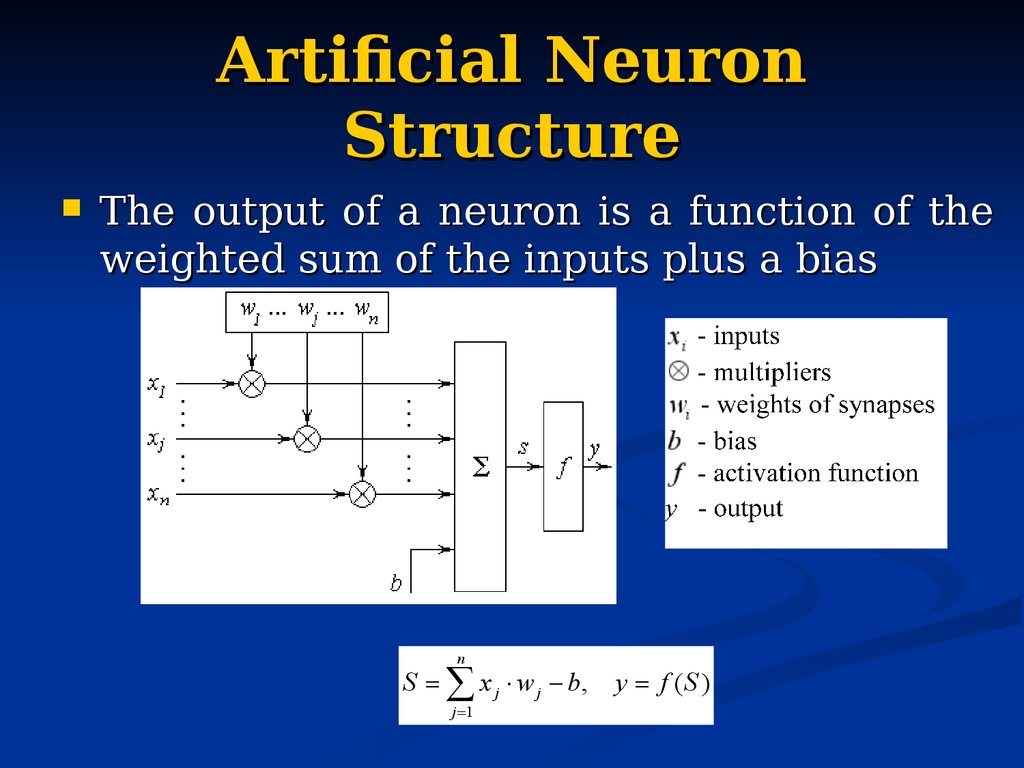
14. Artificial Neuron Structure
The output of a neuron is a function of theweighted sum of the inputs plus a bias
n
S x j w j b,
j 1
y f (S )
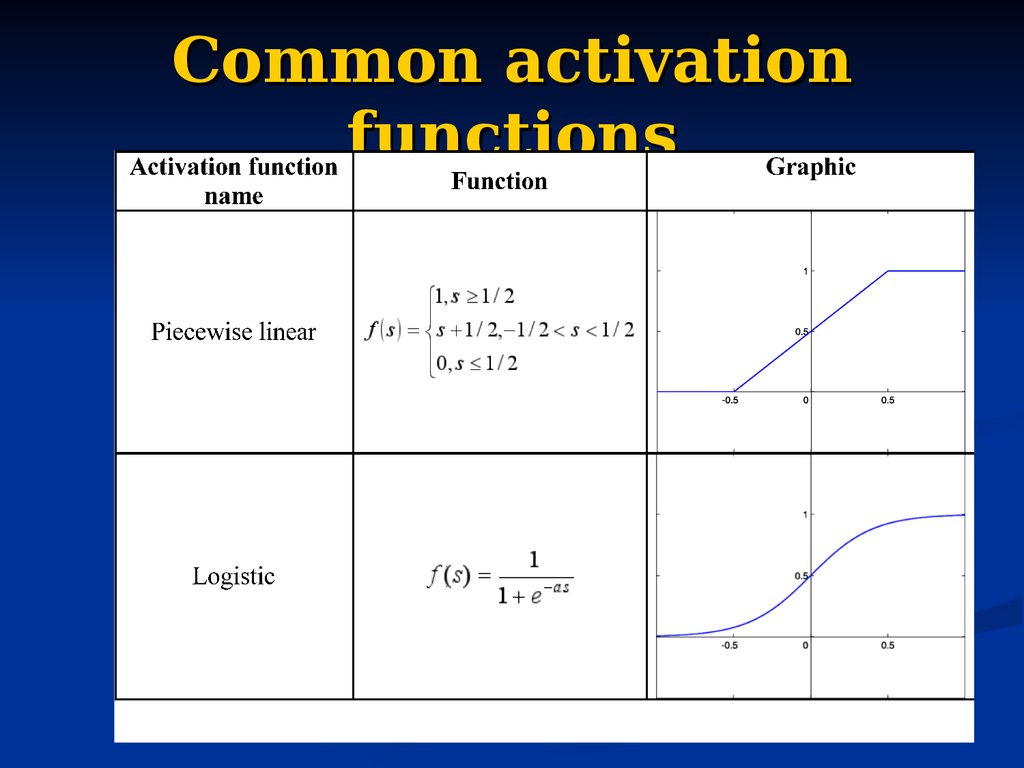
15. Common activation functions
16.
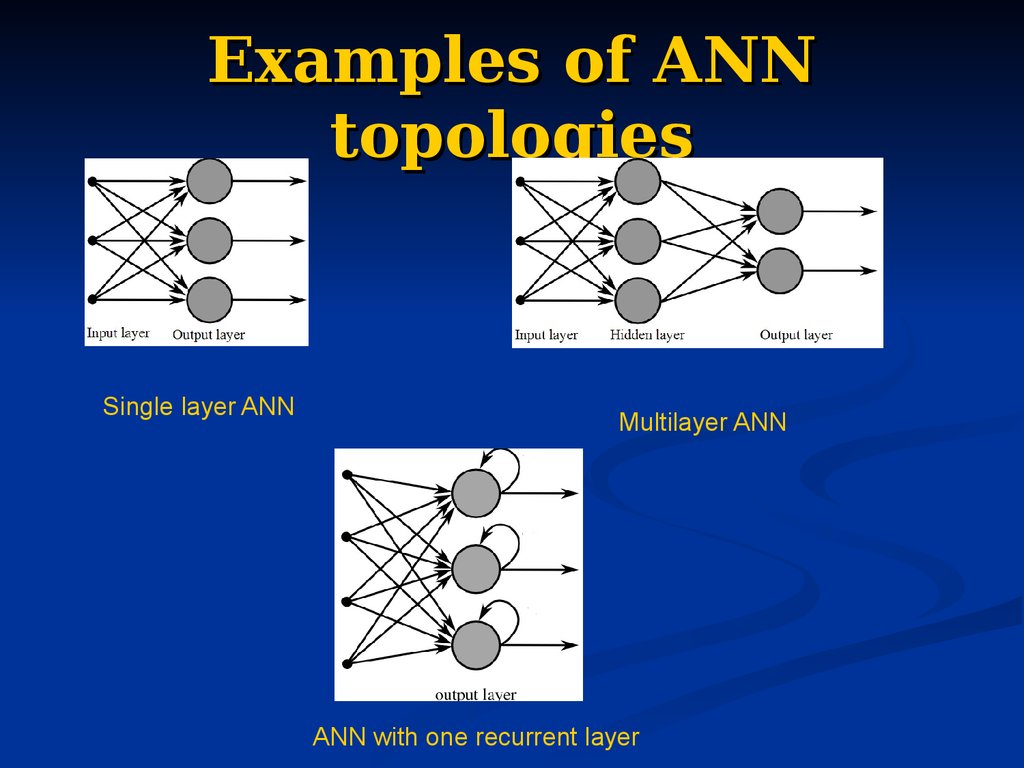
17. Examples of ANN topologies
Single layer ANNMultilayer ANN
ANN with one recurrent layer
18. Fundamentals of learning and training samples
The weights in a neural network are themost important factor in determining its
function.
A training set is a set of training patterns,
which we use to train our neural net.
Training is the act of presenting the
network with some sample data and
modifying
the
weights
to
better
approximate the desired function
19. Fundamentals of learning and training samples
There are two main types of trainingSupervised Training
Supplies the neural network with inputs and the
correct outputs (results).
We can estimate a error vector for certain input.
Response of the network to the inputs is measured.
The weights are modified to reduce the difference
between the actual and desired outputs
Unsupervised Training
The training set only consists of input patterns.
The neural network adjusts its own weights so that
similar inputs cause similar outputs. The network
identifies the patterns and differences in the inputs
without any external assistance
20. Fundamentals of learning and training samples
A training pattern is an input vector pwith the components x1, x2, . . . , xn
whose desired output is known.
By entering the training pattern into
the network we receive an output that
can be compared with the desired
output.
The set of training patterns is called P.
It contains a finite number of ordered
pairs (p, t) of training patterns with
corresponding desired output t.
21. Fundamentals of learning and training samples
Teaching input. Let j be an output neuron.The teaching input tj is the desired and
correct value j should output after the input of
a certain training pattern.
Analogously to the vector p the teaching
inputs t1, t2, . . . , tn of the neurons can also be
combined into a vector t. This vector always
refers to a specific training pattern p and
contained in the set P of the training patterns.
22. Fundamentals of learning and training samples
Error vector. For several output neuronsΩ1,Ω2, . . . ,ΩO the difference between
output vector and teaching input under a
training input p is referred to as error
vector.
t1 y1
E p ...
t y
O
O
23. Fundamentals of learning
Let P be the set of training patters. Inlearning procedure we realize finite
number of iterations or epochs.
Epoch – single presentation of the
entire data to the neural network.
Typically many epochs are required to
train the neural network
Iteration - the process of providing the
network with an single input and
updating the network's weights
24. General learning procedure
Let P be the set of n training patters pnFor i=1 to n
begin
1.
2.
We calculate NN output vector yi for the training
pattern pi.
We compare yi with desired output ti. Then we
calculate the error of output and make modification
of weights.
end
3.
If total error for the training set P more
than some threshold then go to the step 2
25. Using training samples
We have to divide the set of training samplesinto two subsets:
one training set really used to train;
one verification set to test our progress of learning.
The usual division relations are, 70% for
training data and 30% for verification data
(randomly chosen).
We can finish the training process when the
network provides the good results on the
training data as well as on the verification
data.
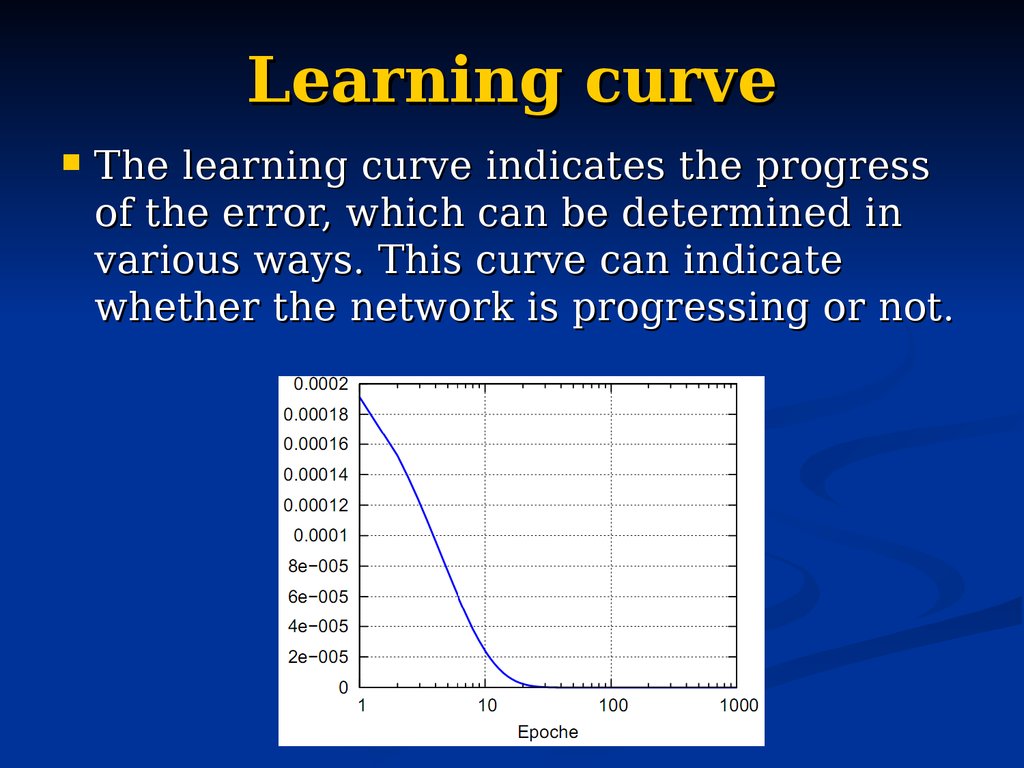
26. Learning curve
The learning curve indicates the progressof the error, which can be determined in
various ways. This curve can indicate
whether the network is progressing or not.
27. Error measurement
Let Ω be the output neuron and O be theset of output neurons.
The specific error Errp is based on a single
training sample.
The total error Err is based on all training samples.
Err
Errp
p P
28. When do we stop learning?
Generally, the training process isstopped when the user in front of the
learning computer "thinks" the error is
small enough.
29. Using neural networks in practice (discussion)
Classificationin marketing: consumer spending pattern classification
In defence: radar and sonar image classification
In medicine: ultrasound and electrocardiogram image
classification, EEGs, medical diagnosis
Recognition and identification
In general computing and telecommunications : speech, vision and
handwriting recognition
In finance: signature verification and bank note verification
Assessment
In engineering: product inspection monitoring and control
In defence: target tracking
In security: motion detection, surveillance image analysis and
fingerprint matching
Forecasting and prediction
In finance: foreign exchange rate and stock market forecasting
In agriculture: crop yield forecasting
In marketing: sales forecasting
In meteorology: weather prediction
30.
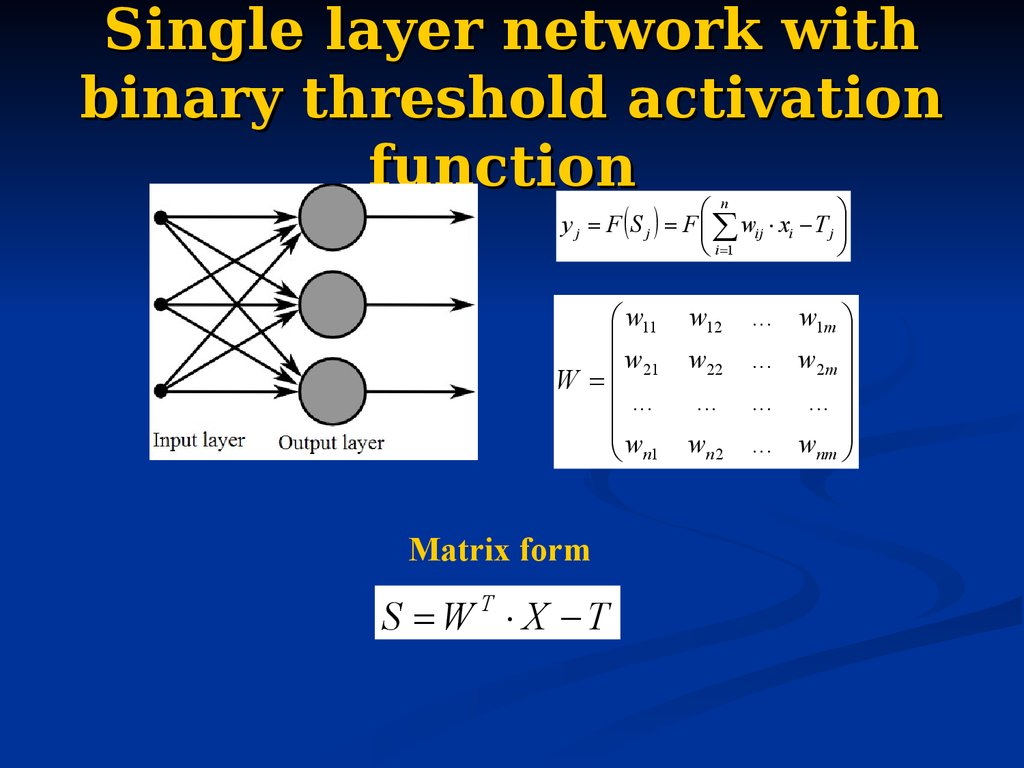
Single layer neural networks31. Single layer network with binary threshold activation function
ny j F S j F wij xi T j
i 1
w11
w21
W
...
w
n1
Matrix form
S W T X T
w12
w22
...
wn 2
... w1m
... w2 m
... ...
... wnm
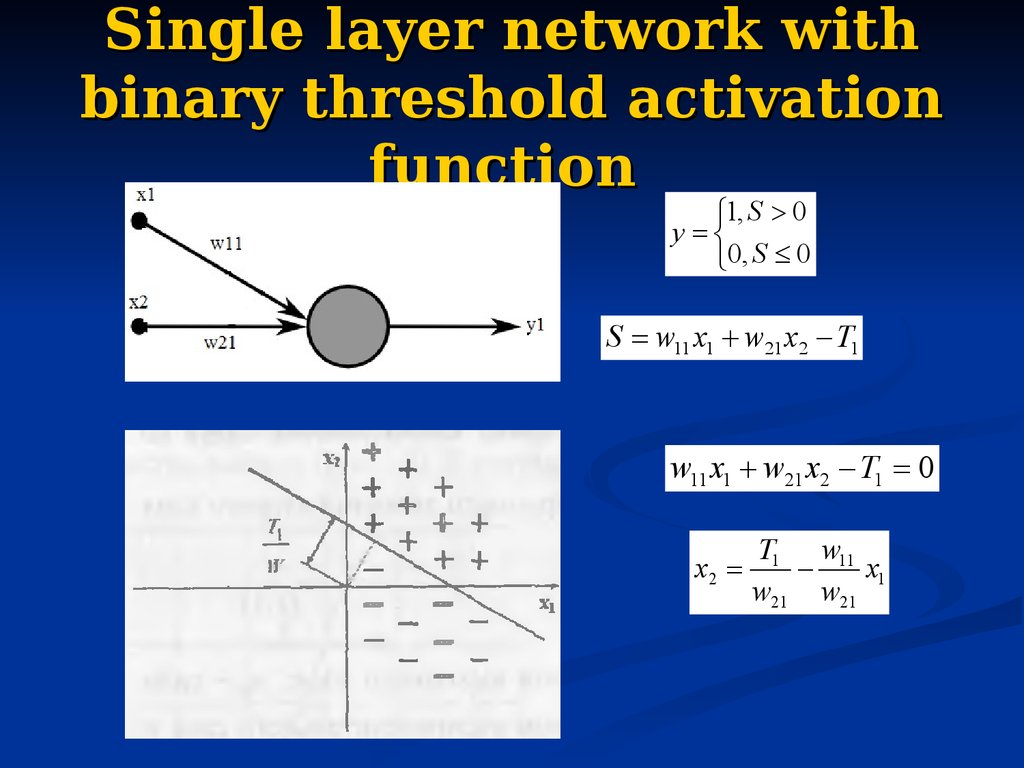
32. Single layer network with binary threshold activation function
1, S 0y
0, S 0
S w11 x1 w21 x2 T1
w11 x1 w21 x2 T1 0
x2
T1 w11
x1
w21 w21
33. Practice with single layer neural network
1.2.
Performing a calculations in single layer
neural networks with using direct and matrix
form. Using various activation functions.
Using single layer neural networks with
binary threshold activation function as linear
classifier. Adjusting the linear classifier
based on training samples.
34. Hebbian learning rule
-Introduced by Donald Hebb in his 1949 book “The Organizationof Behavior”.
-Describes a basic mechanism for synaptic plasticity
wij t 0 0, i, j
wij t 1 wij t xi y j , where t time
S w11 x1 w21 x2 T
w11 t 1 w11 t x1 y1
w21 t 1 w21 t x2 y1
T t 1 T t y1
35. Hebbian learning rule (matrix form)
x112
x1
X
...
L
x1
x12
x22
...
x2L
... x1n
... xn2
, where X i x1i ,..., xni input pattern
... ...
L
... xn
S XW
Y F (S )
W X T Y hebbian learning rule
36. Practice with hebbian learning rule
Construction the neural network basedon hebbian learning rule for modeling
OR logical operator
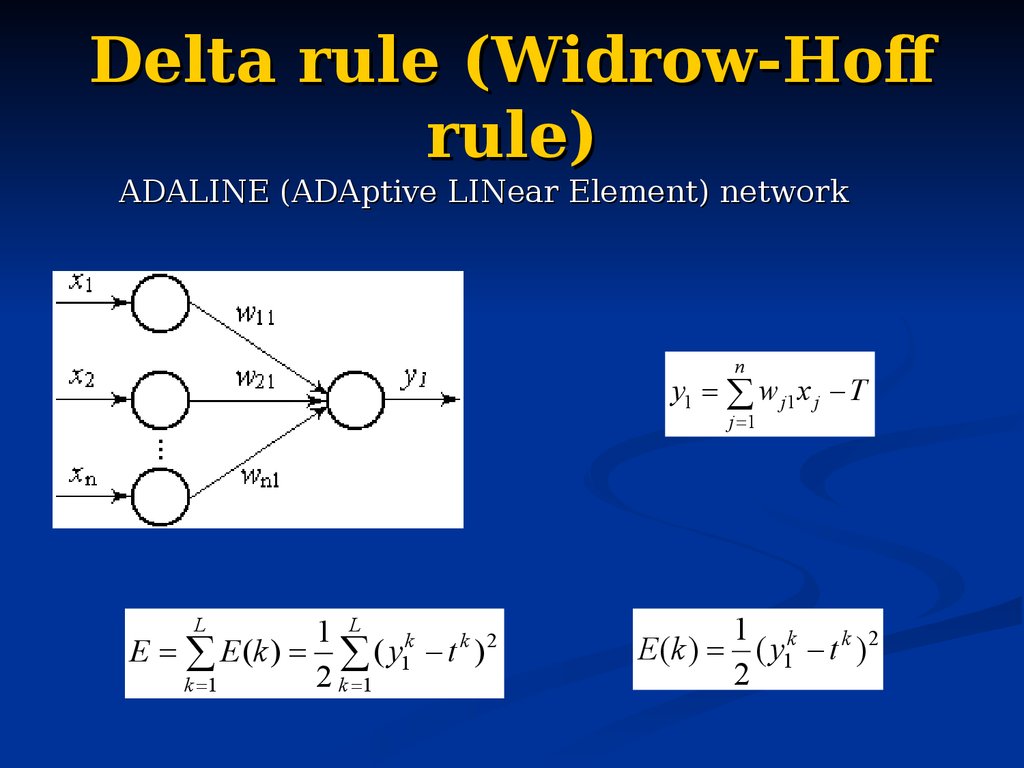
37. Delta rule (Widrow-Hoff rule)
1. The delta rule is a gradient descent learning rule forupdating the weights of the inputs to artificial
neurons in single-layer neural network
2. The goal is to minimize the error between the actual
outputs and the target outputs in the training data
3. For each (input/output) training pair, the delta rule
determines the direction you need to adjust wij to
reduce the error for that training pair.
4. Derivatives are used for teaching
38. Delta rule (Widrow-Hoff rule)
ADALINE (ADAptive LINear Element) networkn
y1 w j1 x j T
j 1
L
1 L k k 2
E E (k ) ( y1 t )
2 k 1
k 1
1
E (k ) ( y1k t k ) 2
2
39. Delta rule (Widrow-Hoff rule)
Gradient descent method: findthe steepest
way
down
the
slope from where you are, and
take a step in that direction
E (k )
w j1 (t 1) w j1 (t )
w j1 (t )
E
E y1k
k
( y1k t k ) x kj
w j1 (t ) y1 w j1
E (k )
T (t 1) T (t )
T (t )
E
E y1k
k
( y1k t k )
T (t ) y1 T
40. Delta rule algorithm
1.2.
3.
4.
5.
Define 0<a<1 and Emin
Initialize the weights with some
small random value
Take input pattern and calculate
output vector.
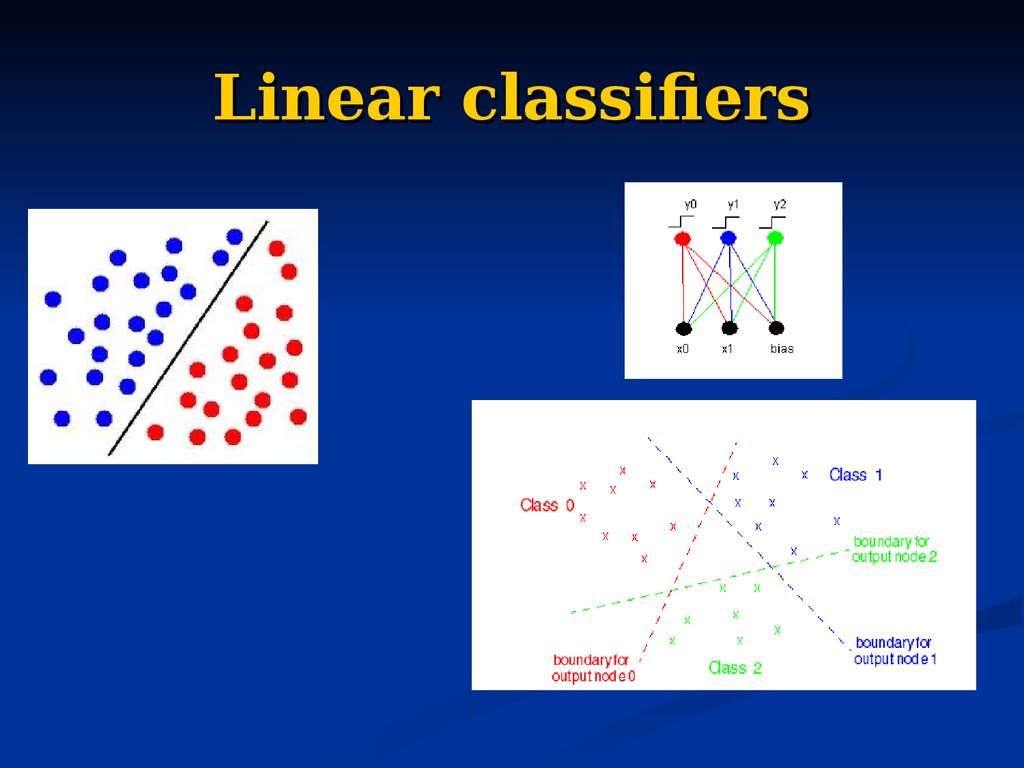
Modify weights and bias according
delta rule.
Do steps 3-4 until E<Emin
41. Linear classifiers
42. Practice with delta rule
Construction the ADALINE neuralnetwork
(linear
classifier
with
minimum error value) based on given
training patterns.
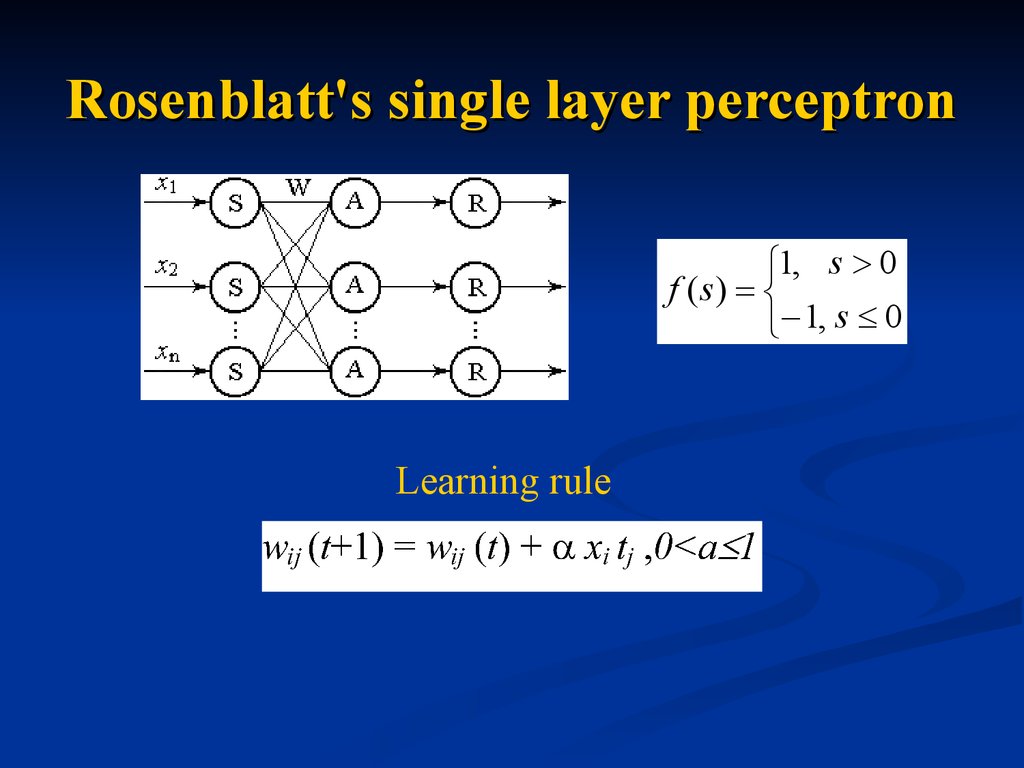
43. Rosenblatt's single layer perceptron
The perceptron is an algorithm forsupervised classification of an input
into one of several possible nonbinary outputs.
It is a type of linear classifier.
Was invented in 1957 by Frank
Rosenblatt as a machine for image
recognition.
44. Rosenblatt's single layer perceptron
1, s 0f (s)
1, s 0
Learning rule
45. Rosenblatt's learning algorithm
1.2.
3.
4.
5.
Initialise the weights and the threshold.
Weights may be initialised to 0 or to a
small random value.
Take input pattern x from X and
calculate output vector y from Y.
If yi=tj then wij will not change.
If yi≠tj then wij(t+1) = wij (t) + xi tj
Do steps 2-4 until yi=tj for whole
training set
46. Rosenblatt's single layer perceptron
Itwas
quickly
proved
that
perceptrons could not be trained to
recognize many classes of patterns.
It is linear classifier. For example, it
is impossible for these classes of
network to learn an XOR function.
47. Practice with Rosenblatt's perceptron
Construction the linear classifier (Rosenblatt’s neuralnetwork perceptron) based on given training patterns.
48. Associative memory
Associative memory (computer science) - adata-storage device in which a location is
identified by its informational content rather
than by names, addresses, or relative
positions, and from which the data may be
retrieved. This memory enable one to retrieve
a piece of data from only a tiny sample of itself.
Associative memory (psychology) - recalling
a previously experienced item by thinking of
something that is linked with it, thus invoking
the association
49. Associative memory
Autoassociativememories
are
capable of retrieving a piece of data
upon presentation of only partial
information from that piece of data
Heteroassociative
memories
can
recall an associated piece of datum
from one category upon presentation
of data from another category.
50. Autoassociative memory based on sign activation function
Neuralstructure:
Activation function
network
1, s 0
f (s)
1, s 0
Number of neurons
in the input layer =
Number of neurons
in the output layer
Learning rule
(adopted hebbian rule)
W XT X
Example:
51. Practice with autoassociative memory
Realization of the associative memorybased on sign activation function.
Working with multiple patterns.
Recognition of the original and noisy
patterns.
Investigation of the properties and
constraints of the associative memory
based on sign activation function.
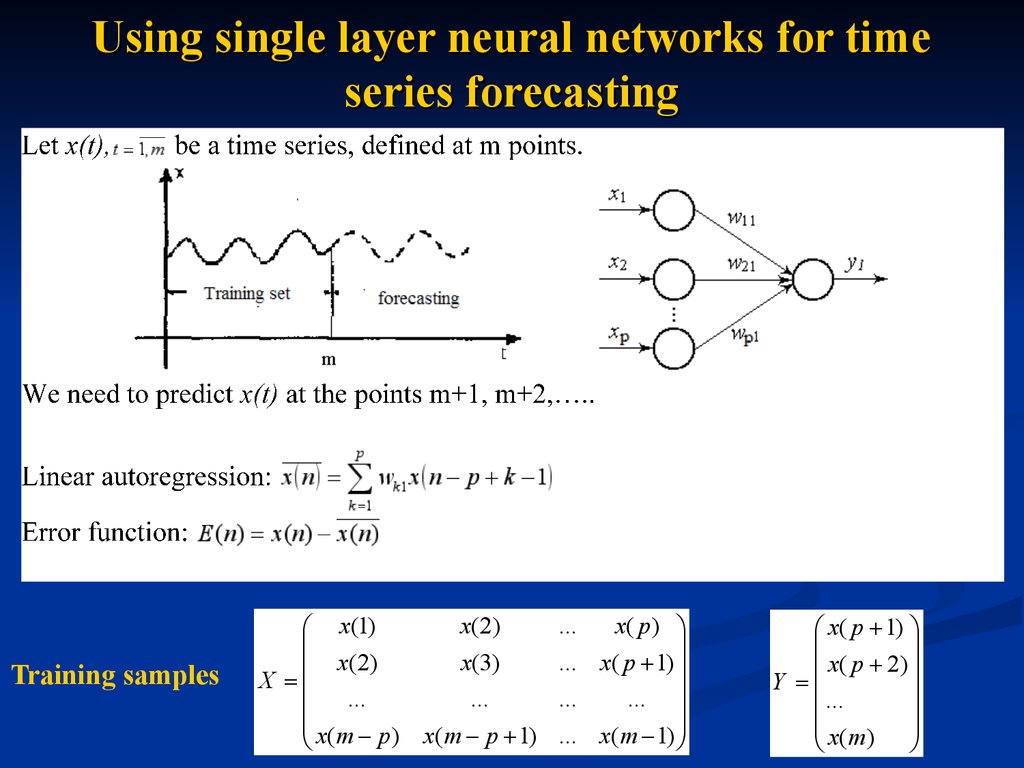
52. Using single layer neural networks for time series forecasting
A time series points, measuredin time spaced
intervals
sequence of data
typically at points
at uniform time
53. Using single layer neural networks for time series forecasting
Training samplesx ( 2)
x(1)
x(3)
x ( 2)
X
...
...
x(m p ) x(m p 1)
x( p )
... x( p 1)
...
...
... x(m 1)
...
x( p 1)
x( p 2)
Y
...
x ( m)
54. Practice with time series forecasting
Using ADALINE neural networks forcurrency forecasting:
Creation the training set from the raw
data (www.val.ru).
Learning the ADALINE.
Training ADALINE network with using
delta rule and estimation the error.
55. Multilayer perceptron
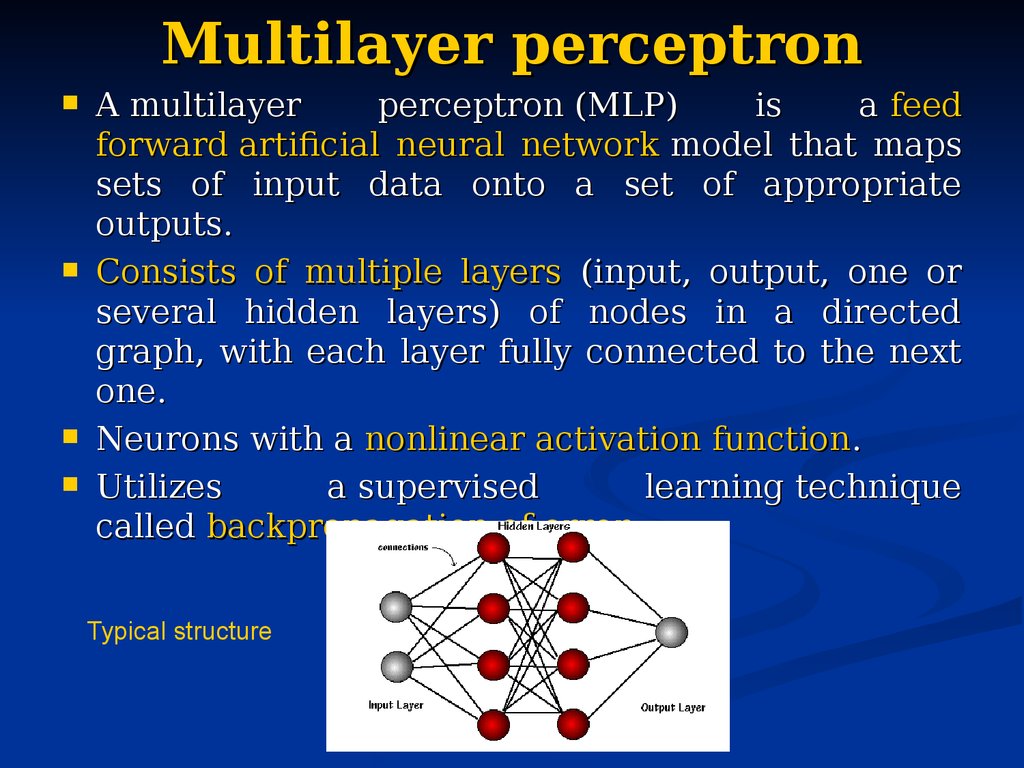
56. Multilayer perceptron
A multilayerperceptron (MLP)
is
a feed
forward artificial neural network model that maps
sets of input data onto a set of appropriate
outputs.
Consists of multiple layers (input, output, one or
several hidden layers) of nodes in a directed
graph, with each layer fully connected to the next
one.
Neurons with a nonlinear activation function.
Utilizes
a supervised
learning technique
called backpropagation of error.
Typical structure
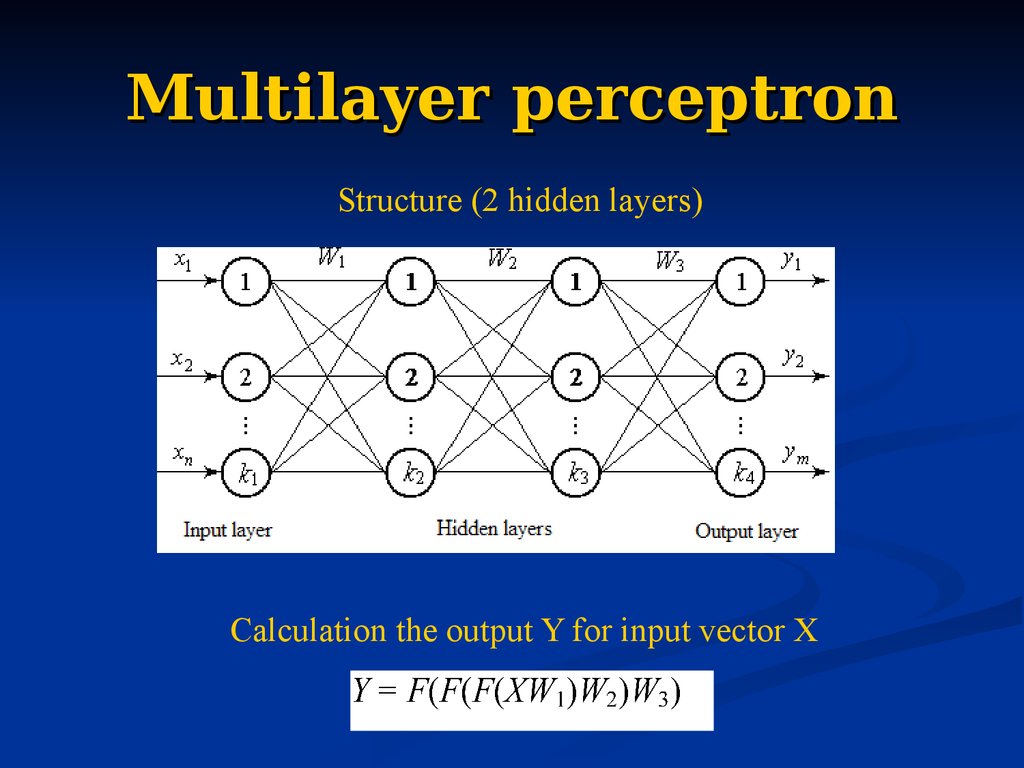
57. Multilayer perceptron
Structure (2 hidden layers)Calculation the output Y for input vector X
58. Multilayer perceptron
Activation function is not a thresholdFunction approximator
Usually a sigmoid function
Not limited to linear problems
Information flows in one direction
The outputs of one layer act as inputs to
the next layer
59. Classification ability
A single layer network can only finda linear discriminant function.
It can divide the input space by
means of hyperplane (straight lines
in two-dimensional space)
60. Classification ability
Universal Function Approximation TheoremMLP with one hidden layer can approximate
arbitrarily closely every continuous function that
maps intervals of real numbers to some output
interval of real numbers
f:[0,1]n->[0,1]
2n+1 neurons in hidden layer.
Can form single convex
decision regions
One hidden layer is sufficient
for the large majority of problems
61. Classification ability
Any function can be approximated to arbitraryaccuracy by a network with two hidden layers
MLP with two hidden layers can classify sets of
any form. It can form arbitrary disjoint decision
regions
62. Backpropagation algorithm
D. Rumelhart, G. Hinton, R. Williams (1986)Most common method of obtaining the
weights in the multilayer perceptron
A form of supervised training
The basic backpropagation algorithm is
based on minimizing the error of the
network using the derivatives of the error
function
Backpropagation of error generalizes the
delta rule
63. Basic steps
Forward propagation of a trainingpattern's input through the neural
network in order to generate the
propagation's output activations.
Backward propagation of the
output’s error through the neural
network using the training pattern
target in order to generate the deltas
of all output and hidden neurons.
64. Backpropagation
65. Backpropagation
We use gradient descent method forminimizing the error
66. Backpropagation
Theorem. For any hidden layer i of the neuralnetwork, error of the neuron i calculates by
recursive way through the errors of neurons of
the next layer j.
m
i j F ( S j ) wij
j 1
where m – number of neurons in the next layer j
wij – weights between neuron i and neurons in the
next layer j
Sj – weighted sum for the neuron j in next layer.
Proof
67. Backpropagation
Theorem. We can calculate derivatives of errorE through the weights w and bias T by
following way.
Proof
68. Backpropagation
Backpropagation rule69. Backpropagation algorithm
the training speed (0< <1) anddesired minimal error Em
2.Initialize the weights and biases by random
way.
3.Take consequently all input patterns x from X.
1.Define
y j F ( vector
wij yi T j ) y by following way
Calculate output
i
Realize backpropogation shceme by following
way
ij
j
i
Modify ijweights
and j biases
by following way
w (t 1) w (t ) F ( S ) y
T j (t 1) T j (t ) j F ( S j )
70. Backpropagation algorithm
4. Calculate overall error for all patterns1 L
E ( y kj t kj ) 2
2 k 1 j
5. If E>Em then go to the step 3.
71. Practice. Calculation delta-rule expressions for various activation functions
72. Some problems
The learning rate is importantToo small
Convergence extremely slow
Too large
May not converge
The result may
converge to
a local minimum.
Possible decision:
Using adaptive
learning rate
73. Some problems
OverfittingThe number of hidden neurons is very important, it defines the
complexity of the decision boundary:
Too few
Underfit the data – it does not have enough free
parameters to fit the training data well.
Too many
Overfit the data – NN learns the insignificant details
Try different number and use validation set to choose the
best one.
Start small and increase the number until satisfactory results
are obtained.
74.
What constitutes a “good” trainingset?
Samples must represent the general
population
Samples must contain members of each
class
Samples in each class must contain a
wide range of variations or noise effect
75. Practice with multilayer perceptron
1.2.
Using MLP for noisy digits
recognition &
Using MLP for time series
forecasting.
- Training set preparation.
- MLP learning in Deductor software.
- Estimation the error.
76. Recurrent neural networks
Capable to influence to themselvesby means of recurrences, e.g. by
including the network output in the
following computation steps.
Hopfield neural network
Hamming neural network
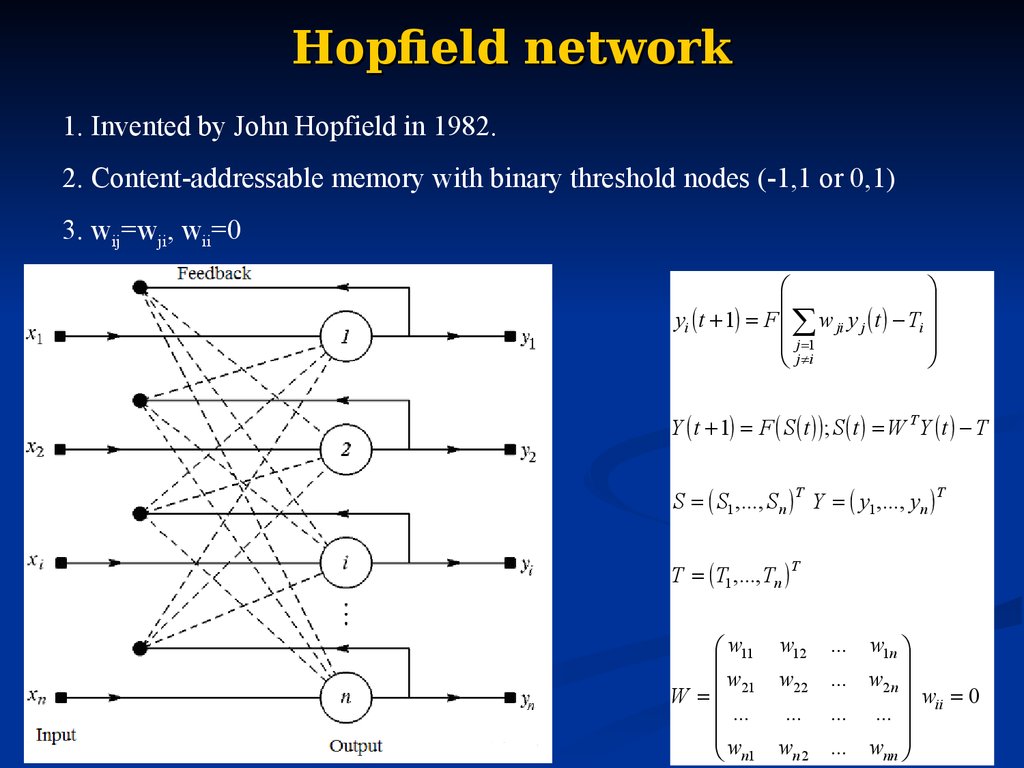
77. Hopfield network
1. Invented by John Hopfield in 1982.2. Content-addressable memory with binary threshold nodes (-1,1 or 0,1)
3. wij=wji, wii=0
yi t 1 F w ji y j t Ti
j 1
j i
Y t 1 F S t ; S t W T Y t T
S S1 ,..., S n Y y1 ,..., yn
T
T T1 ,..., Tn
w11
w
W 21
...
wn1
T
T
w12
w22
...
wn 2
... w1n
... w2 n
wii 0
... ...
... wnn
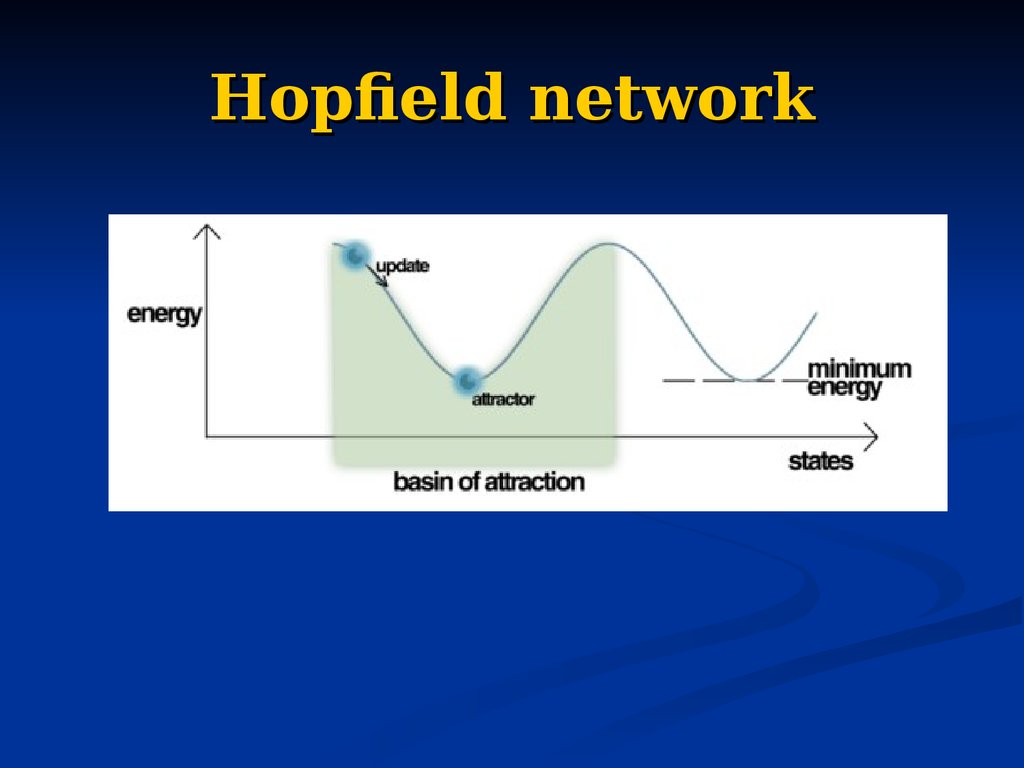
78. Hopfield network
79. Hopfield network as associative memory
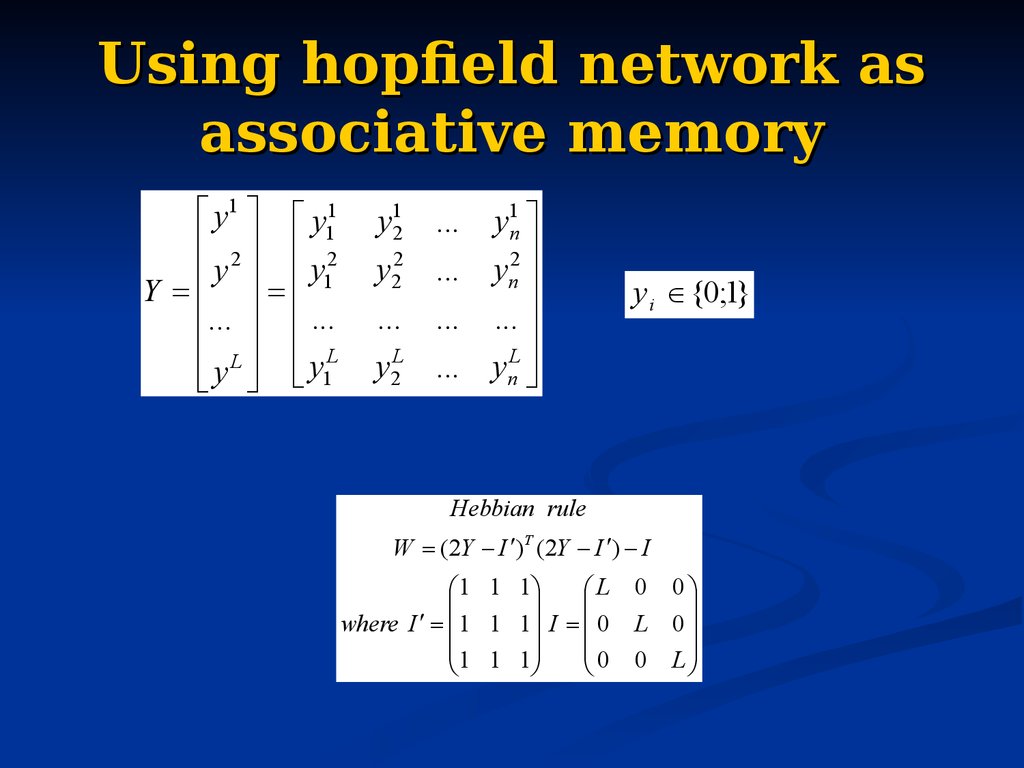
80. Using hopfield network as associative memory
y1 y112 2
y
y
Y 1
... ...
L
y L y1
y12
y22
...
y2L
y1n
2
... yn
... ...
L
... yn
...
y i {0;1}
Hebbian rule
W (2Y I )T (2Y I ) I
1 1 1
L 0 0
where I 1 1 1 I 0 L 0
1 1 1
0 0 L
81. Hopfield network as associative memory
1.2.
Take noisy pattern y
Realize iterations
yi (t 1) F w ji y j (t )
j
1, S 0
sign( S )
0, S 0
3.
Until we will not reach stable state
(attractor)
82. Example
83. Practice with Hopfield network
Realization of the associative memorybased on Hopfield Neural Network
Working with multiple patterns.
Recognition of the original and noisy
patterns.
Investigation of the properties and
constraints of the associative memory
based on Hopfield network.
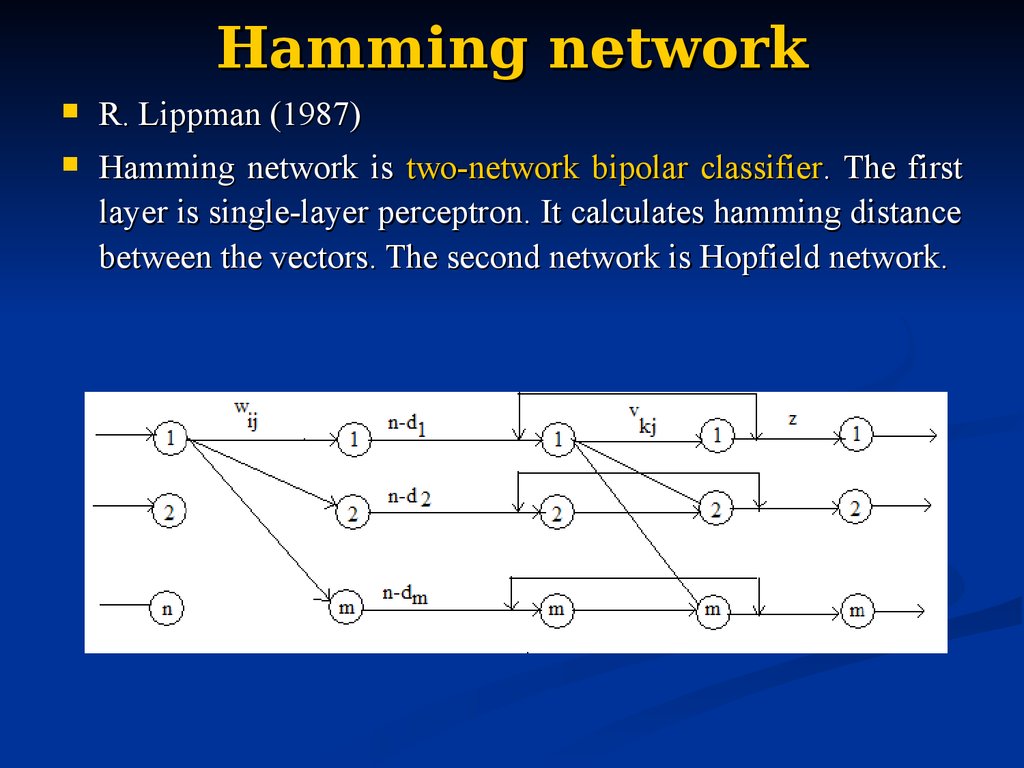
84. Hamming network
R. Lippman (1987)Hamming network is two-network bipolar classifier. The first
layer is single-layer perceptron. It calculates hamming distance
between the vectors. The second network is Hopfield network.
85. Hamming network
X 1 x11 ,..., x1n X 2 x12 ,..., xn2 X m x1m ,..., xnmwij xij / 2 , T j n / 2
yj dj
d j Hamming distance between input pattern and j stored pattern
1, if k j
vkj
, e const ,0 e 1 / m
e, if k j
S j , S j 0
z j F S j
0, S j 0
86. Hamming network working algorithm
Define weights wij, TjGet input pattern and initialize
Hopfield weights
Make iterations in Hopfield network
until we get stable output.
Take output neuron with 1 value.
87. Self-organizing maps
88. Self-organizing maps
Unsupervised TrainingThe training set only consists of input
patterns.
The neural network adjusts its own weights
so that similar inputs cause similar outputs.
The network identifies the patterns and
differences in the inputs without any
external assistance
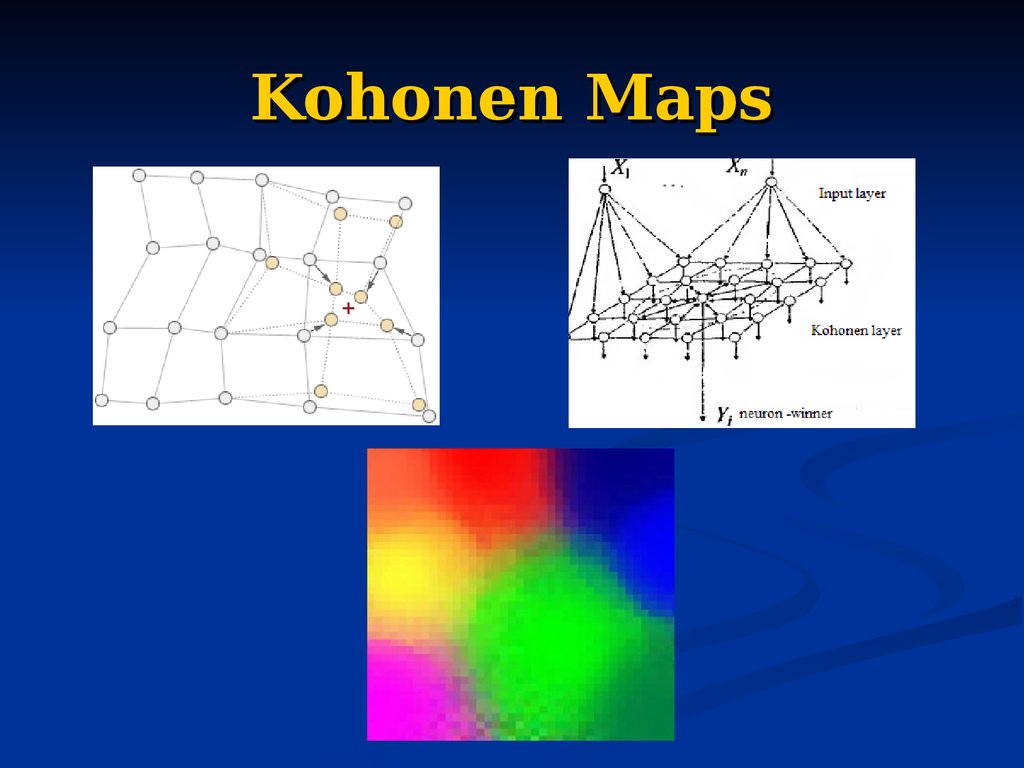
89. Self-organizing maps (SOM)
A self-organizing map (SOM) is a type ofartificial neural network that is trained using
unsupervised learning to
produce
a
lowdimensional
(typically
two-dimensional),
discretized representation of the input space of
the training samples, called a map.
Self-organizing maps are different from other
artificial neural networks in the sense that they
use a neighborhood function to preserve the
topological properties of the input space.
The model was first described as an artificial
neural network by the Finnish professor Teuvo
Kohonen.
90. Self-organizing maps
We only ask which neuron is active at themoment.
We are not interested in the exact output of the
neuron but in knowing which neuron provides
output.
These networks widely used for clustering
SOMs (like our brain) decide the task of
mapping
a
high-dimensional
input
(N
dimensions) onto areas in a low-dimensional
grid of cells (G dimensions).
91.
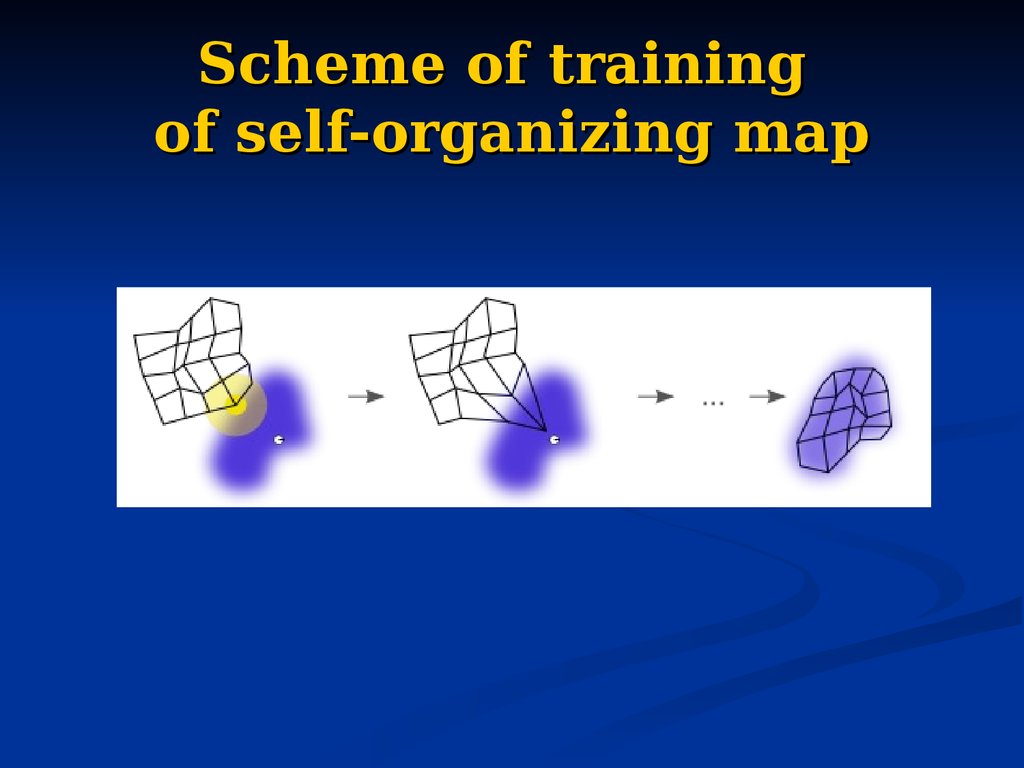
92. Scheme of training of self-organizing map
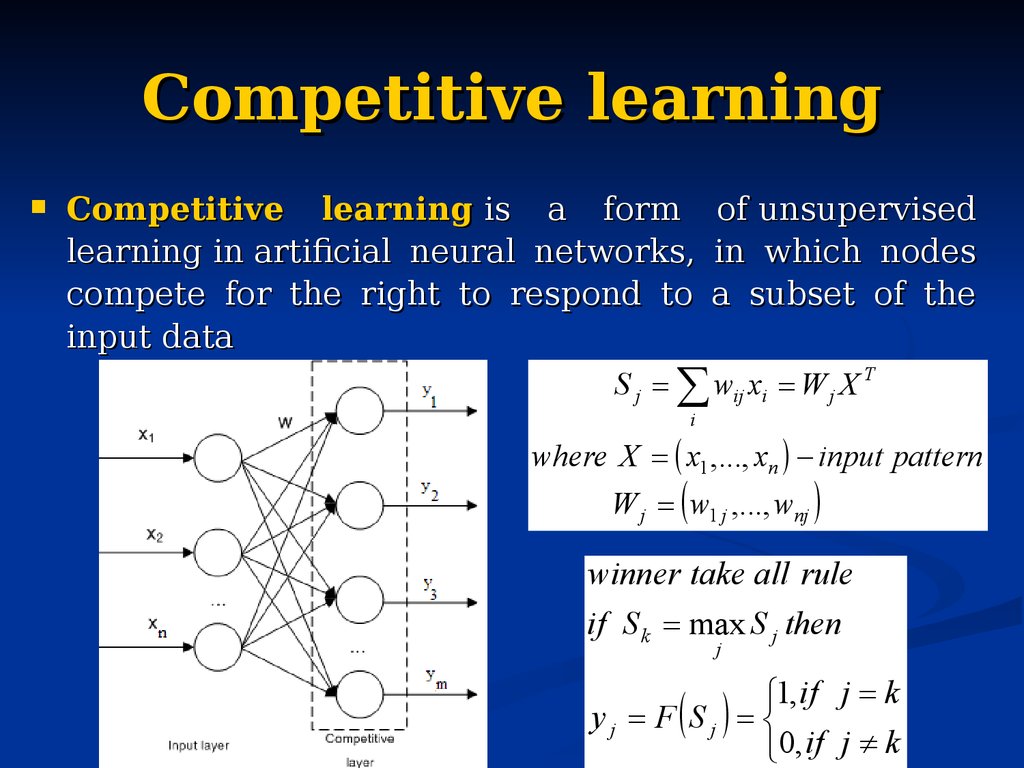
93. Competitive learning
Competitive learning is a form of unsupervisedlearning in artificial neural networks, in which nodes
compete for the right to respond to a subset of the
input data
S j wij xi W j X T
i
where X x1 ,..., xn input pattern
W j w1 j ,..., wnj
winner take all rule
if S k max S j then
j
1, if j k
y j F S j
0, if j k
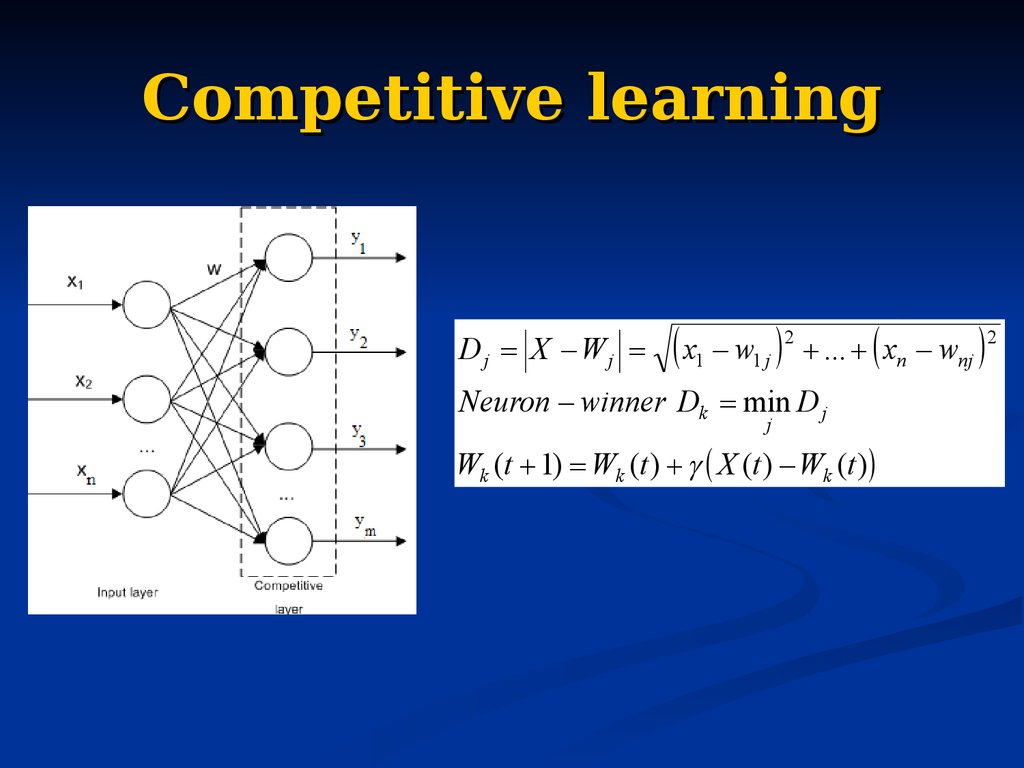
94. Competitive learning
Dj X Wjx1 w1 j 2 ... xn wnj 2
Neuron winner Dk min D j
j
Wk (t 1) Wk (t ) X (t ) Wk (t )
95. Vector quantization
It works by dividing a large set ofpoints (vectors) into groups having
approximately the same number of
points closest to them. Each group is
represented by its centroid point, as
in k-means and
some
other clustering algorithms.
96. Vector quantization
Choose random weights from[0;1].
t=1
Take all input patterns Xl,l=1,L
D lj X l W j
pattern
recognition
x1 w1 j 2 ... xn wnj 2
Neuron winner Dkl min D lj
j
Applications:
data compression
Video codecs
wij (t 1) wij (t ) (t ) xi wij (t ) , j k
QuickTime
wij (t 1) wij (t ), j k
(t ) 1 / t
Cinepak
Indeo etc.
t=t+1
Audio codecs
Ogg Vorbis
TwinVQ
DTS etc.
97. Kohonen Maps
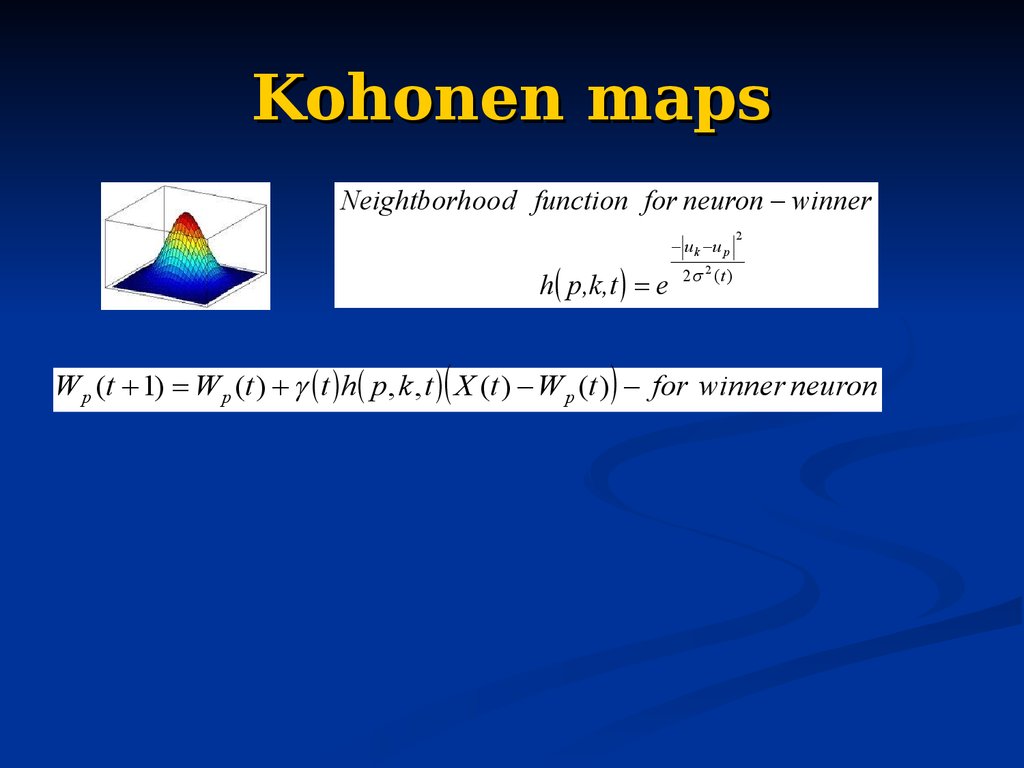
98. Kohonen maps
Neightborh ood function for neuron winnerh p,k,t e
u k u p
2
2 2 ( t )
W p (t 1) W p (t ) t h p, k , t X (t ) W p (t ) for winner neuron
99. Kohonen maps learning procedure
1.Choose random weights from [0;1].
2.
t=1
3.
Take input pattern Xl and calculate Dij=(Xl-Wij),where i,j=1,m
4.
Detect winner neuron D(k1,k2)=min(Dij)
5.
Calculate for every output neuron
uk u p
h p,k,t e
6.
2
2 2 ( t )
Modify weights by following way
W p (t 1) W p (t ) t h p, k , t X (t ) W p (t ) for winner neuron
Repeat steps 3-6 for all input patterns
100. Training and Testing
101. Training
The goal is to achieve a balancebetween correct responses for the
training patterns and correct
responses for new patterns.
102. Training and Verification
The set of all known samples isbroken into two independent sets
Training set
A group of samples used to train the neural
network
Testing set
A group of samples used to test the
performance of the neural network
Used to estimate the error rate
103. Verification
Provides an unbiased test of the qualityof the network
Common error is to “test” the neural
network using the same samples that
were used to train the neural network.
The network was optimized on these
samples, and will obviously perform well on
them
Doesn’t give any indication as to how well
the network will be able to classify inputs
that weren’t in the training set
104. Summary (Discussion)
Artificial neural networks are inspired by the learningprocesses that take place in biological systems.
Artificial neurons and neural networks try to imitate
the working mechanisms of their biological
counterparts.
Learning can be perceived as an optimisation
process.
Biological neural learning happens by the
modification of the synaptic strength. Artificial neural
networks learn in the same way.
The synapse strength modification rules for artificial
neural networks can be derived by applying
mathematical optimisation methods.
105. Summary
Learning tasks of artificial neural networks canbe reformulated as function approximation
tasks.
Neural networks can be considered as nonlinear
function approximating tools (i.e., linear
combinations of nonlinear basis functions),
where the parameters of the networks should be
found by applying optimisation methods.
The optimisation is done with respect to the
approximation error measure.
In general it is enough to have a single hidden
layer neural network (MLP or other) to learn the
approximation of a nonlinear function.



















































































 Информатика
Информатика Английский язык
Английский язык








