Похожие презентации:
Гидродинамика. Закон Бернулли. Гидравлические сопротивления и гидравлические потери
1.
Тема 2:гидродинамика
УЧЕБНЫЕ ВОПРОСЫ
:
1. Основные понятия гидродинамики.
2. Закон Бернулли (энергетический и
графический смысл).
3. Режимы движения жидкости.
4. Гидравлические сопротивления и
гидравлические потери.
2.
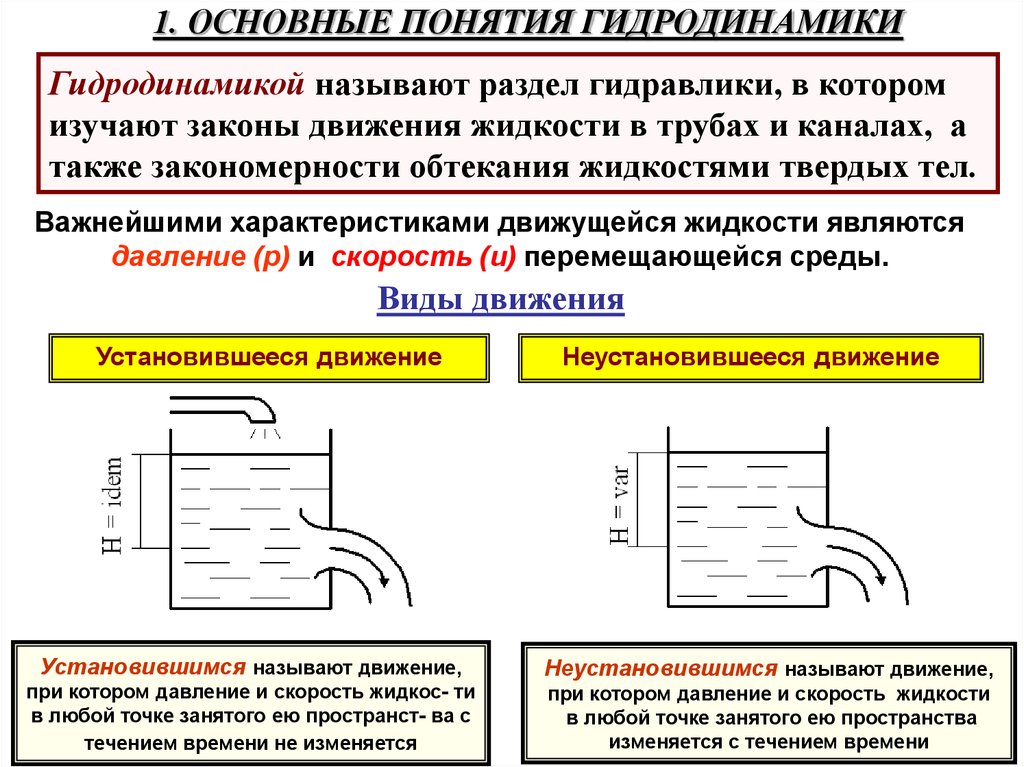
1. ОСНОВНЫЕ ПОНЯТИЯ ГИДРОДИНАМИКИГидродинамикой называют раздел гидравлики, в котором
изучают законы движения жидкости в трубах и каналах, а
также закономерности обтекания жидкостями твердых тел.
Важнейшими характеристиками движущейся жидкости являются
давление (р) и скорость (u) перемещающейся среды.
Виды движения
Установившееся движение
Установившимся называют движение,
при котором давление и скорость жидкос- ти
в любой точке занятого ею пространст- ва с
течением времени не изменяется
Неустановившееся движение
Неустановившимся называют движение,
при котором давление и скорость жидкости
в любой точке занятого ею пространства
изменяется с течением времени
3.
Равномерноедвижение
Неравномерное
движение
Равномерным
Неравномерным
называют движение,
при котором давление
и скорость жидкости
не изменяются по
длине потока
называют движение,
при котором давление
и скорость жидкости
изменяются по длине
потока
4.
Напорноедвижение
Напорное движение –
это движение жидкости в
закрытых
трубопроводах при полном заполнении жидкостью его поперечного сечения
Безнапорное
движение
Безнапорное движение –
это движение капельной
жидкости при наличии
свободной поверхности
5.
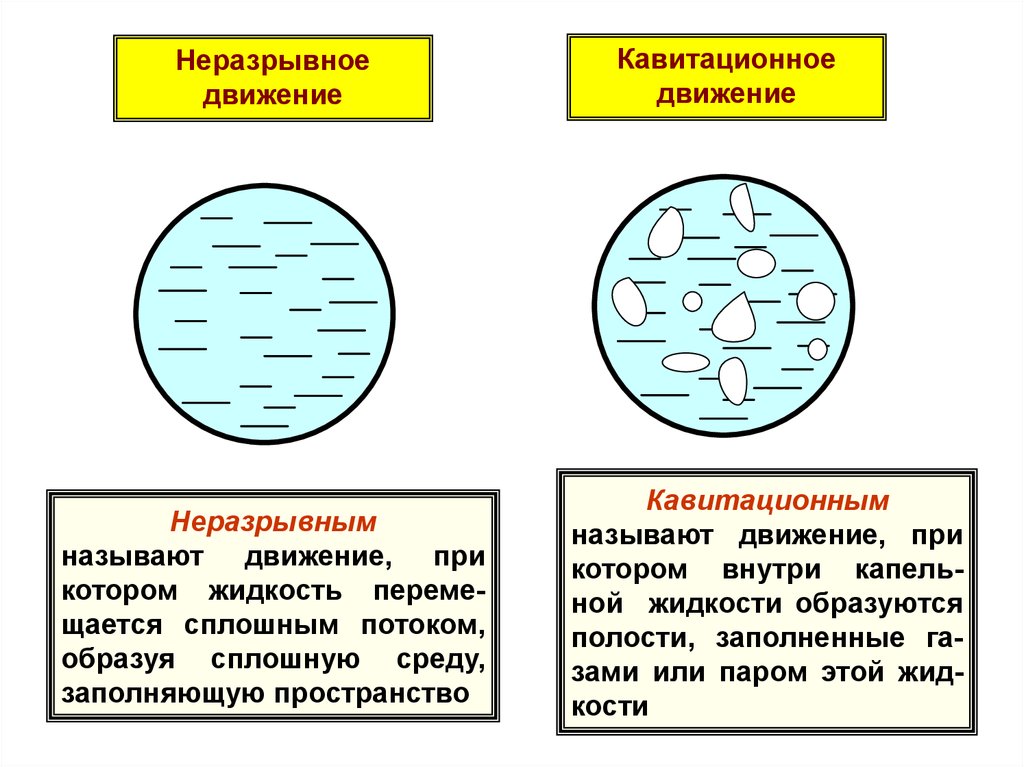
Неразрывноедвижение
Неразрывным
называют движение, при
котором жидкость перемещается сплошным потоком,
образуя сплошную среду,
заполняющую пространство
Кавитационное
движение
Кавитационным
называют движение, при
котором внутри капельной жидкости образуются
полости, заполненные газами или паром этой жидкости
6.
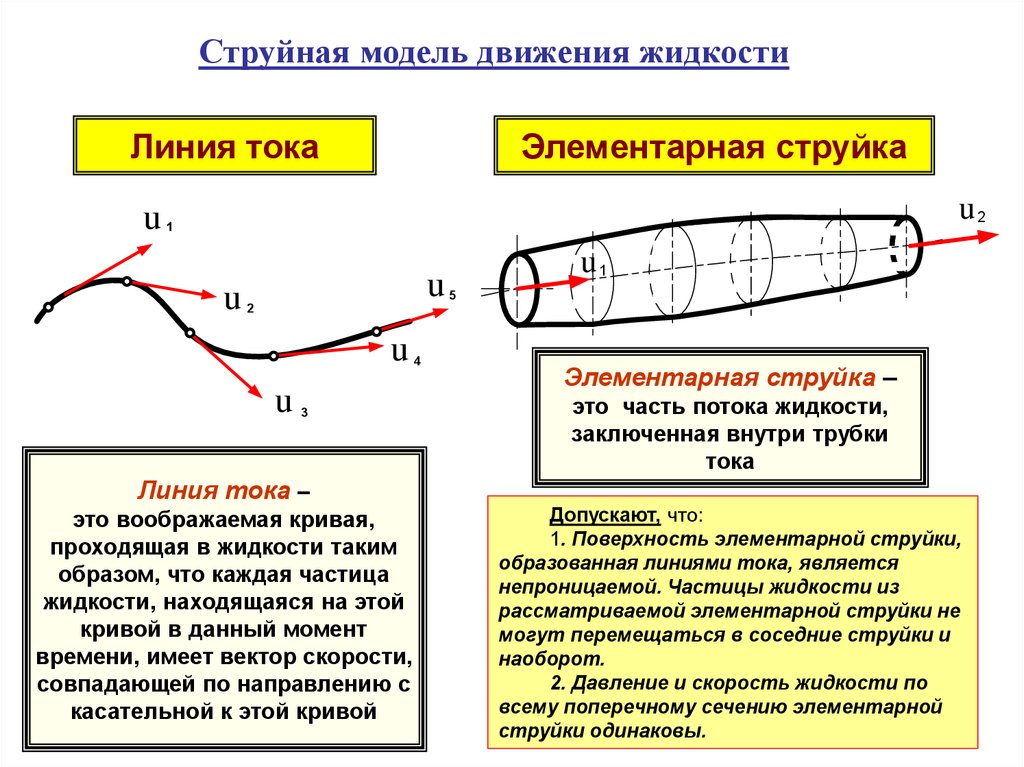
Струйная модель движения жидкостиЛиния тока
u
Элементарная струйка
u2
1
u
u
2
u
u
3
Линия тока –
это воображаемая кривая,
проходящая в жидкости таким
образом, что каждая частица
жидкости, находящаяся на этой
кривой в данный момент
времени, имеет вектор скорости,
совпадающей по направлению с
касательной к этой кривой
4
u1
5
Элементарная струйка –
это часть потока жидкости,
заключенная внутри трубки
тока
Допускают, что:
1. Поверхность элементарной струйки,
образованная линиями тока, является
непроницаемой. Частицы жидкости из
рассматриваемой элементарной струйки не
могут перемещаться в соседние струйки и
наоборот.
2. Давление и скорость жидкости по
всему поперечному сечению элементарной
струйки одинаковы.
7.
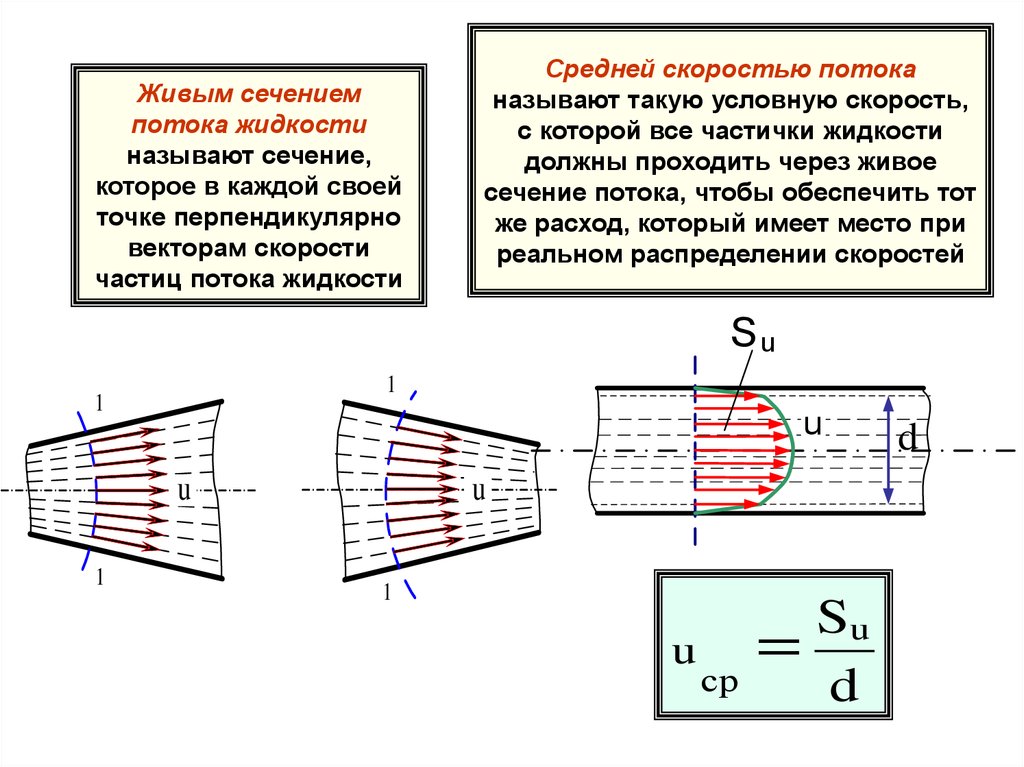
Живым сечениемпотока жидкости
называют сечение,
которое в каждой своей
точке перпендикулярно
векторам скорости
частиц потока жидкости
Средней скоростью потока
называют такую условную скорость,
с которой все частички жидкости
должны проходить через живое
сечение потока, чтобы обеспечить тот
же расход, который имеет место при
реальном распределении скоростей
Su
1
1
u
u
1
u
1
u
ср
Su
d
d
8.
Расход и средняя скорость потокаРасход жидкости - это ее количество, протекающее через
живое сечение потока в единицу времени
объемный (Qv)
массовый (Qm)
Для элементарной струйки жидкости:
dQv = u·dS, м3/с;
dQm = ρ·u·dS, кг/с.
Для потока жидкости:
Qv u·dS= uср·S, м3/с;
Qm = ρ·u·dS= ρ·uср·S, кг/с.
9.
Уравнение неразрывности (сплошности)Закон неразрывности потока жидкости является частным случаем закона
сохранения массы. Смысл рассматриваемого закона: в потоке, движущейся капельной жидкости отсутствуют разрывы струи. (Нарушение неразрывности потока капельной жидкости возможно при кавитационном
движении). Следствием сказанного является одинаковая величина расхода
жидкости через любое живое сечение.
2
1
u1
S1
1
u2
S2
2
Q v u1ср S1 u 2ср S2 u iср Si idem
u1 ср S2
u 2 ср S1
10.
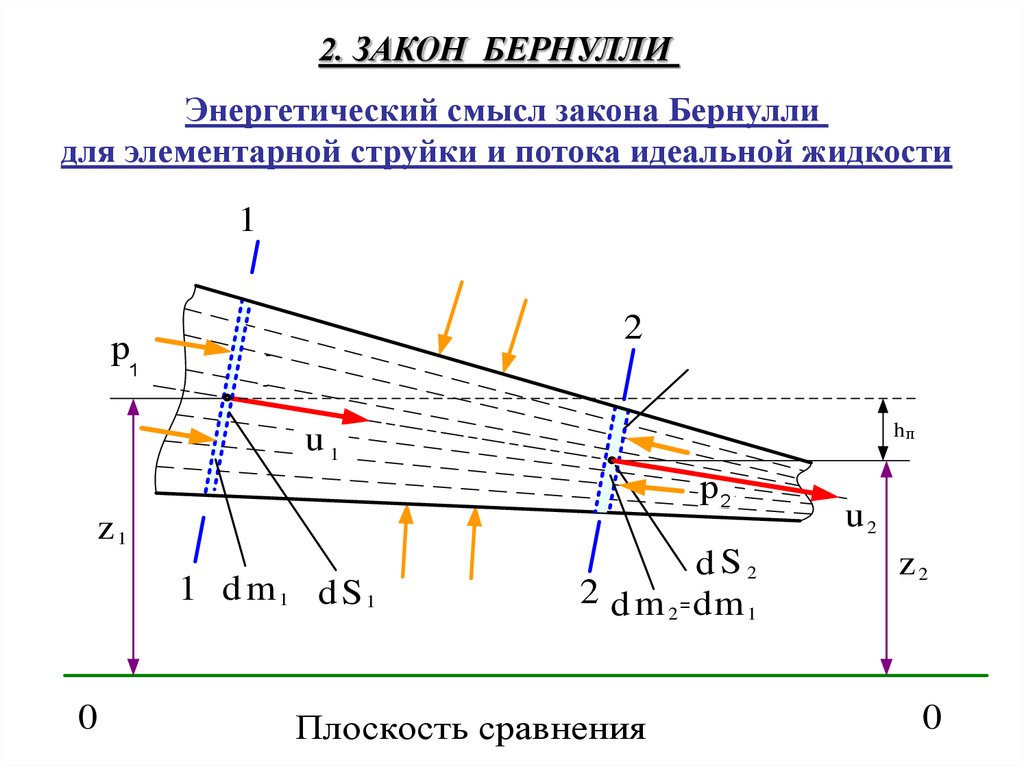
2. ЗАКОН БЕРНУЛЛИЭнергетический смысл закона Бернулли
для элементарной струйки и потока идеальной жидкости
1
2
р
1
hп
u1
р2
z1
1 d m1 d S1
0
dS2
2 d m 2 = dm 1
Плоскость сравнения
u2
z2
0
11.
Уравнение Бернулли для идеальной жидкостиdm1 g z1 dm1
p1
ρ
2
dm1
u1
2
dm2 g z 2 dm2
p2
ρ
2
dm
u2
2
(1)
2
Все члены уравнения (1) имеют размерность «джоуль» и представляют собой ту или
иную составляющую энергии движущейся жидкости:
dm1 g z1 и dm2 g z2 - это потенциальные энергии жидкости в сечениях 1-1 и 2-2 в
поле сил тяжести (при ее отсчете от условного начала - плоскости сравнения 0-0);
p1
, dm p 2 - это потенциальные энергии жидкости в сечениях 1-1 и 2-2
2
ρ
ρ 2 в поле сил давления;
2
u1
u
dm1
, dm 2 2 - это кинетические энергии жидкости в сечениях 1-1 и 2-2.
2
2
dm1
Учитывая, что dm1=dm2, после деления левой и правой частей формулы (1)
на g и dm, получим
p1
u12
p2
u 22
z1
z2
(2)
ρ g
2 g
ρ g
2 g
Зависимости (1) и (2) получены для произвольно выбранных сечений 1-1 и 2-2,
то эти равенства можно продолжать для любых других сечений струйки
жидкости. Поэтому
2
p
u
dm g z dm g dm g idem
ρ
2
(3)
p
u2
z
idem
ρ g 2 g
(4)
12.
z - это удельные потенциальные энергии жидкостив поле сил тяжести в сечениях 1-1 и 2-2 –
геометрические напоры;
p - это удельные потенциальные энергии жидкости
ρ g в поле сил давления в сечениях 1-1 и 2-2 –
потенциальные напоры.
u 2 - это удельные кинетические энергии жидкости
2 g в сечениях 1-1 и 2-2 – скоростные напоры.
13.
Энергетический смысл закона Бернуллидля элементарной струйки и потока реальной жидкости
dm g z1 dm
p
1
ρ
dm
u2
1
2
dm g z dm
2
p
2
ρ
dm
u2
2
2
dm g h п
(1)
Все члены уравнения (1) имеют размерность «джоуль» и представляют собой ту или
иную составляющую энергии движущейся жидкости:
dm z1 и dm g z2 - это потенциальные энергии жидкости в сечениях 1-1 и 2-2 в
поле сил тяжести (при ее отсчете от условного начала - плоскости сравнения 0-0);
dm
dm
p1
ρ
2
u1
2
, dm
p2
- это
потенциальные энергии жидкости в сечениях 1-1 и 2-2
ρ в поле сил давления;
2
u2
, dm 2 - это кинетические энергии жидкости в сечениях 1-1 и 2-2;
dm hп - это затраты энергии («потери» знергии) на перемещение жидкости
от сечения 1-1 до сечения 2-2.
После деления левой и правой частей формулы (1) на g и dm, получим
p1
u12
p2
u 22
z1
z2
hn
ρ g 2 g
ρ g 2 g
(2)
14.
Уравнение Бернулли для потока реальной жидкостиУравнение Бернулли для потока реальной жидкости отличается от
уравнения Бернулли для элементарной струйки реальной жидкости
по двум причинам.
Прежде всего, для элементарной струйки скорость движения
частиц жидкости во всех точках рассматриваемого поперечного
сечения принималась одинаковой. В потоке же реальной жидкости
скорость ее частиц в различных точках поперечного сечения
различна. Поэтому в расчет вводят среднюю скорость.
Возможные варианты распределения скорости потока
жидкости по сечению трубы
u
u
15.
Однако рассчитанное по средней скорости значение удельнойкинетической энергии потока оказывается несколько меньше ее
действительной величины. Поэтому вводят поправочный коэффициент
который называют коэффициентом неравномерности
распределения скоростей по сечению. Величина
зависит от вида режима движения жидкости (которые будут далее).
α-
коэффициент, учитывающий неравномерность
распределения скоростей по живому сечению
потока
В результате уравнение Бернулли для потока реальной жидкости в
удельной форме получает вид:
p1
z1
ρ g
α1 u12ср
2 g
p2
z2
ρ g
i n
h n h тр h м i
i 1
α 2 u 22 ср
2 g
hn
16.
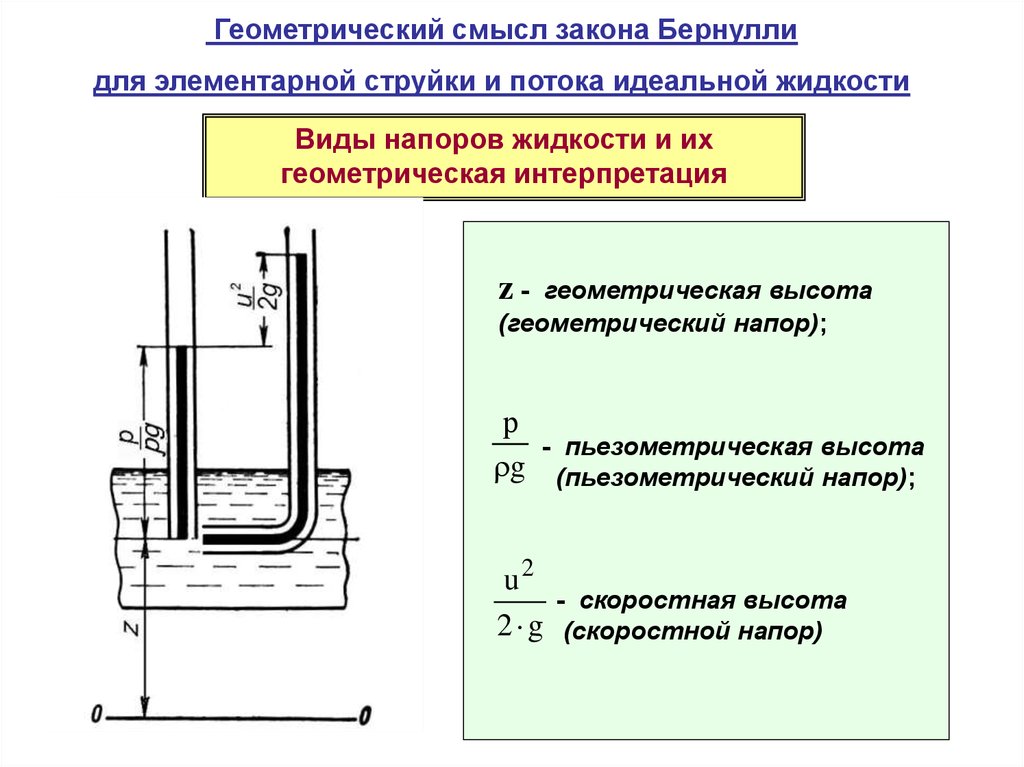
Геометрический смысл закона Бернуллидля элементарной струйки и потока идеальной жидкости
Виды напоров жидкости и их
геометрическая интерпретация
z-
геометрическая высота
(геометрический напор);
р
- пьезометрическая высота
g (пьезометрический напор);
u2
- скоростная высота
2 g (скоростной напор)
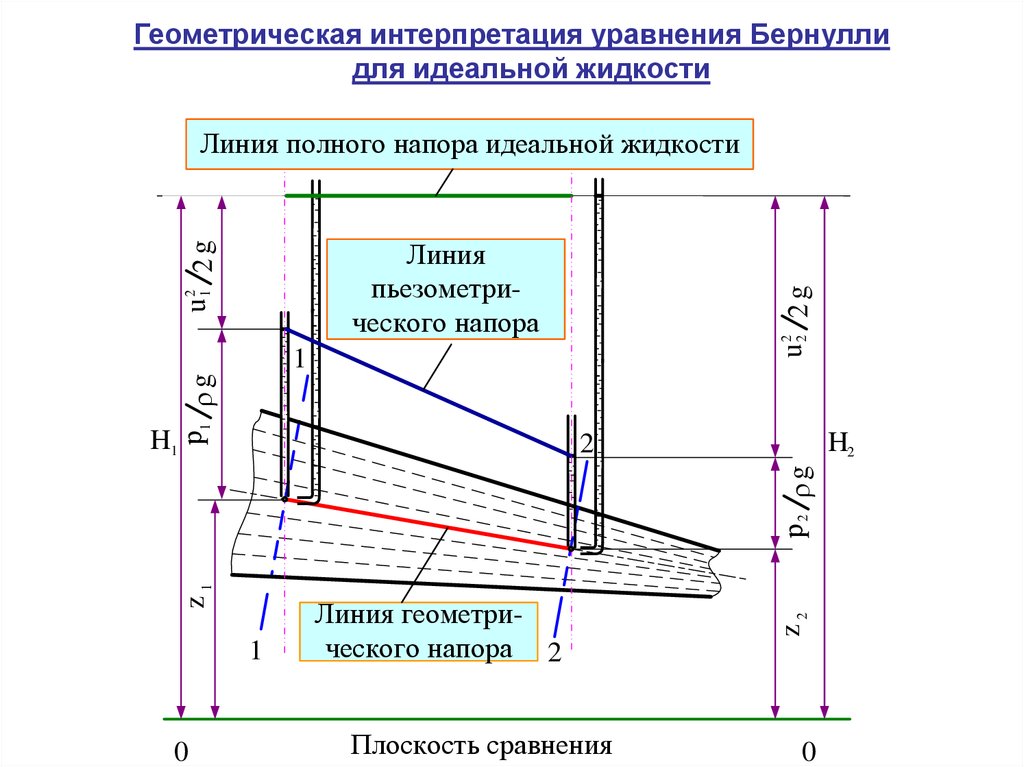
17.
Геометрическая интерпретация уравнения Бернуллидля идеальной жидкости
Линия полного напора идеальной жидкости
u 22 2 g
u 21 2 g
Линия
пьезометрического напора
р1 g
1
H1
H2
1
0
Линия геометрического напора 2
Плоскость сравнения
z2
z1
р2 g
2
0
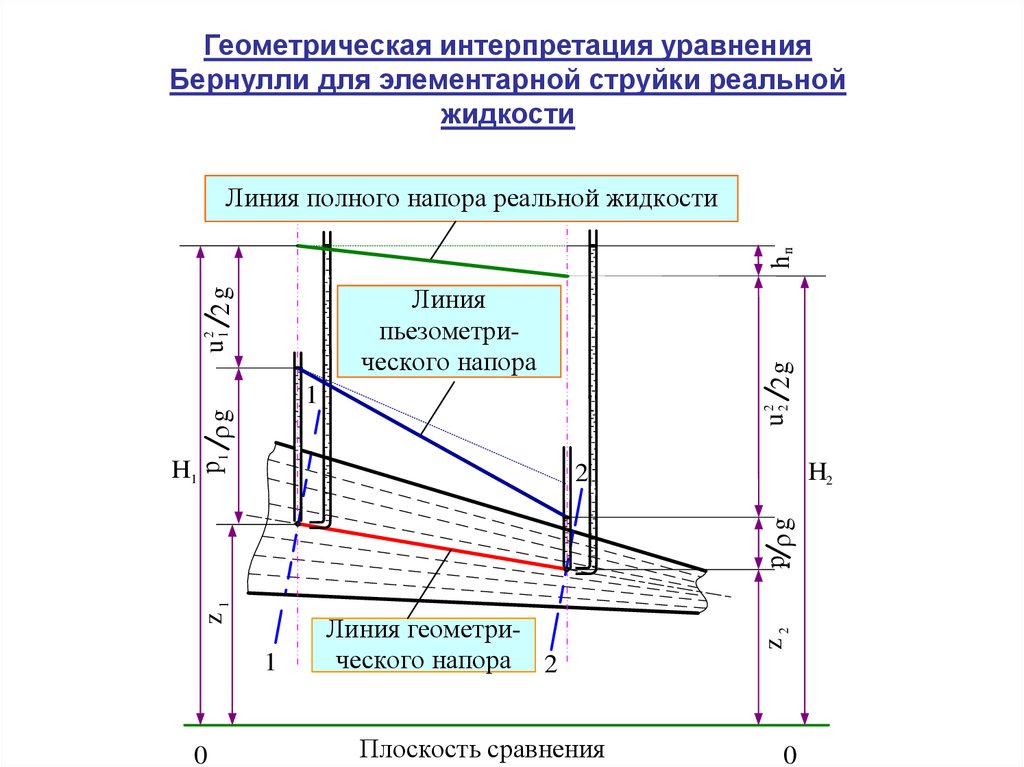
18.
Геометрическая интерпретация уравненияБернулли для элементарной струйки реальной
жидкости
hп
Линия полного напора реальной жидкости
u 22 2 g
u 21 2 g
Линия
пьезометрического напора
р1 g
1
H1
H2
1
0
Линия геометрического напора 2
Плоскость сравнения
z2
z1
2
р g
2
0
19.
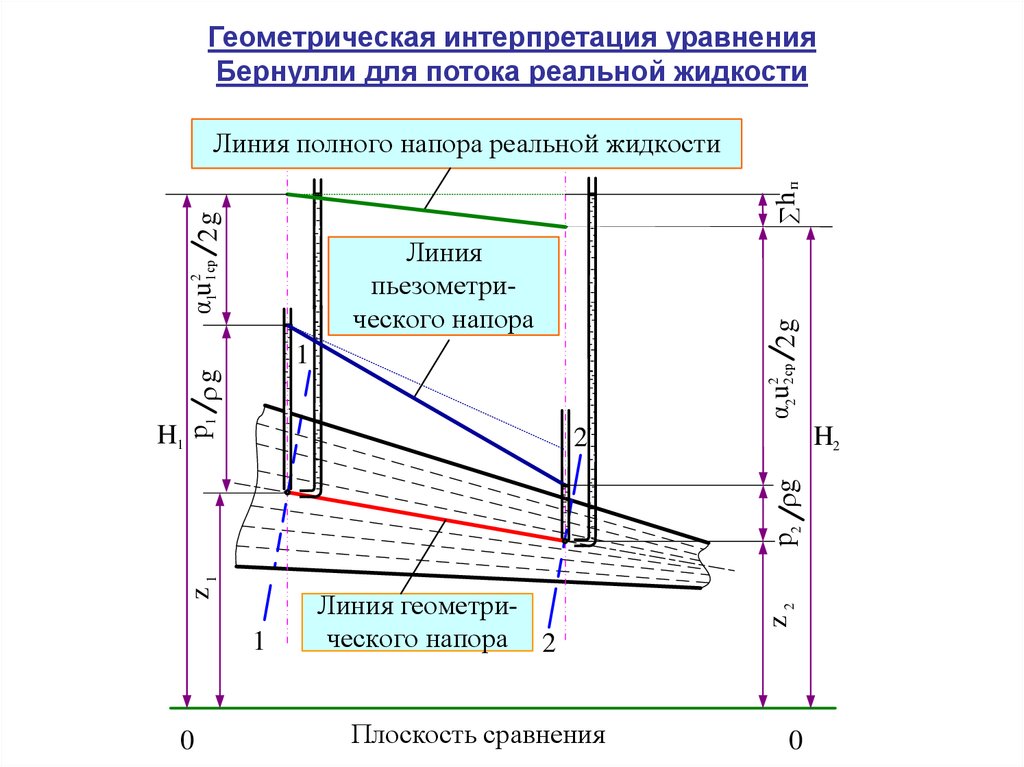
Геометрическая интерпретация уравненияБернулли для потока реальной жидкости
hп
Линия полного напора реальной жидкости
α1u 21 ср 2 g
α2u 22ср 2 g
Линия
пьезометрического напора
р1 g
1
H1
H2
1
0
Линия геометрического напора 2
Плоскость сравнения
z2
z1
р2 g
2
0
20.
3. РЕЖИМЫ ДВИЖЕНИЯ ЖИДКОСТИЛаминарный
Ламинарным (от латинского слова
«lamina» - лента, пластина)
называют слоистое течение жидкости
без перемешивания ее частиц и без
пульсаций скоростей и давления
Турбулентный
Турбулентным (от латинского слова
«turbulentus» - беспорядочный)
называют течение жидкости,
сопровождающееся интенсивным
перемешиванием ее частиц и
пульсациями скоростей и давлений
21.
Распределение скоростейпо живому сечению потока жидкости
Ламинарный подслой
d
1
1
u
u
1
1
Ламинарный
режим
Турбулентный
режим
22.
Число РейнольдсаЛаминарный
(Re < 2320)
ud экв
Re
Турбулентный
(Re 2320)
Турбулентный
переходный
(2320 < Re <4000)
Если сечение канала не круглое,
то вместо диаметра
используется, так называемый,
приведенный (эквивалентный)
диаметр
d экв
Турбулентный
развитый
(Re > 4000)
4S
П
23.
4. ГИДРАВЛИЧЕСКИЕ СОПРОТИВЛЕНИЯИ ГИДРАВЛИЧЕСКИЕ ПОТЕРИ
Гидравлическими сопротивлениями называют все,
что вызывает необходимость затрачивать («терять»)
энергию для обеспечения перемещения жидкости (вязкость
жидкости, трение ее о стенки канала, резкие изменения
формы, величины сечения или конфигурации каналов, по
которым движется жидкость)
Энергию, затрачиваемую на преодоление гидравлических
сопротивлений называют «потерями» энергии.
«Потери» удельной энергии (напора) или, как их часто называют, гидравлические потери, зависят от конструктивных
параметров гидравлических устройств, скорости течения и
вязкости жидкости, а иногда и от давления в ней.
24.
Гидравлические потери пропорциональны скороститечения жидкости во второй степени.
Гидравлические потери полного напора определяются по
формулам:
в единицах давления
hn g h u
где
2
cр
/ 2,
Па,
- безразмерный коэффициент пропорциональности,
называемый коэффициентом потерь, или
коэффициентом сопротивления.
в линейных единицах
hn
2
u ср
/ 2g
,м
25.
ГИДРАВЛИЧЕСКИЕ ПОТЕРИ(ПОТЕРИ НАПОРА)
Гидравлические
потери (потери
напора) на трение
(по длине)
Обусловлены преодолением
вязкостных сил трения
Местные
гидравлические
потери (местные
потери напора)
Обусловлены преодолением
местных гидравлических
сопротивлений
h п h тр h м
26.
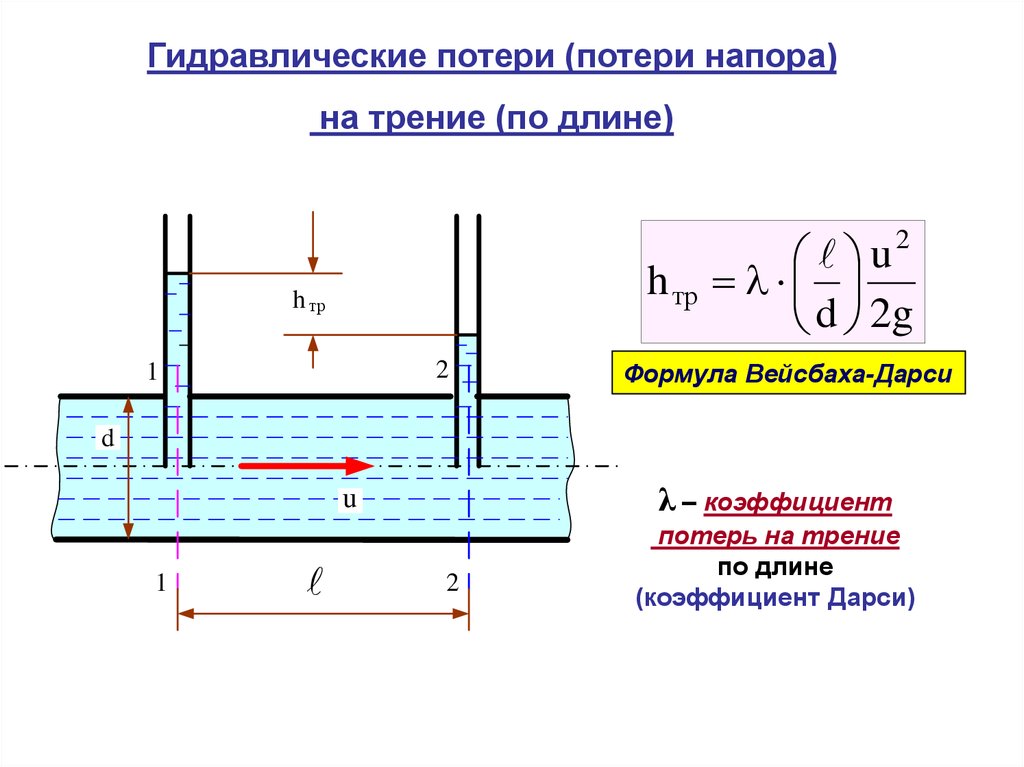
Гидравлические потери (потери напора)на трение (по длине)
u
d 2g
2
h тр
h тр
2
1
Формула Вейсбаха-Дарси
d
λ – коэффициент
u
1
2
потерь на трение
по длине
(коэффициент Дарси)
27.
Определение коэффициента потерь натрение (по длине) при ламинарном
режиме движения
(Re 2320)
64
Re
Уравнение Пуазейля
.
D
Δ - абсолютная шероховатость - это среднее значение
размеров выступов на внутренней поверхности канала. Если
Δ<0,I мм, то трубы называют гладкими; при Δ=0,I-I,0 мм – шероховатыми; если Δ>I,0 мм- трубы считают очень шероховатыми.
28.
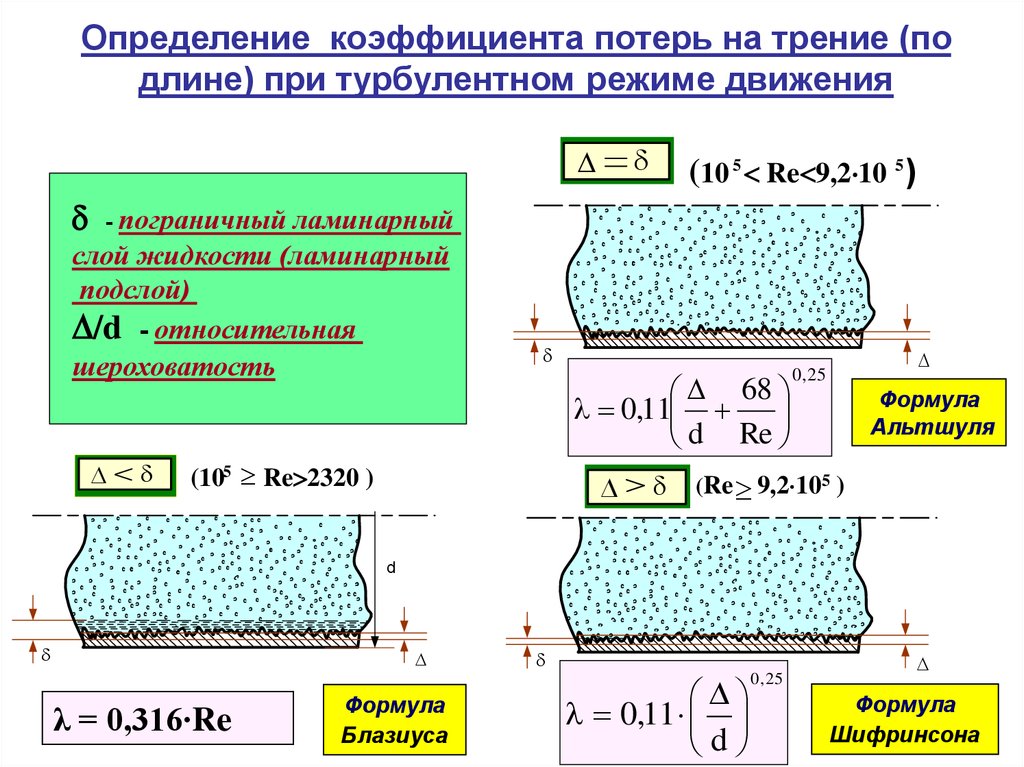
Определение коэффициента потерь на трение (подлине) при турбулентном режиме движения
d
D
(10 5 Re 9,2 10 5 )
d - пограничный ламинарный
слой жидкости (ламинарный
подслой)
D/d - относительная
шероховатость
D
d
d
D 68
0,11
d
Re
(105 Re 2320 )
D
d
D
0 , 25
Формула
Альтшуля
(Re 9,2 105 )
d
d
D
λ = 0,316∙Re
Формула
Блазиуса
d
D
0,11
d
0 , 25
D
Формула
Шифринсона
29.
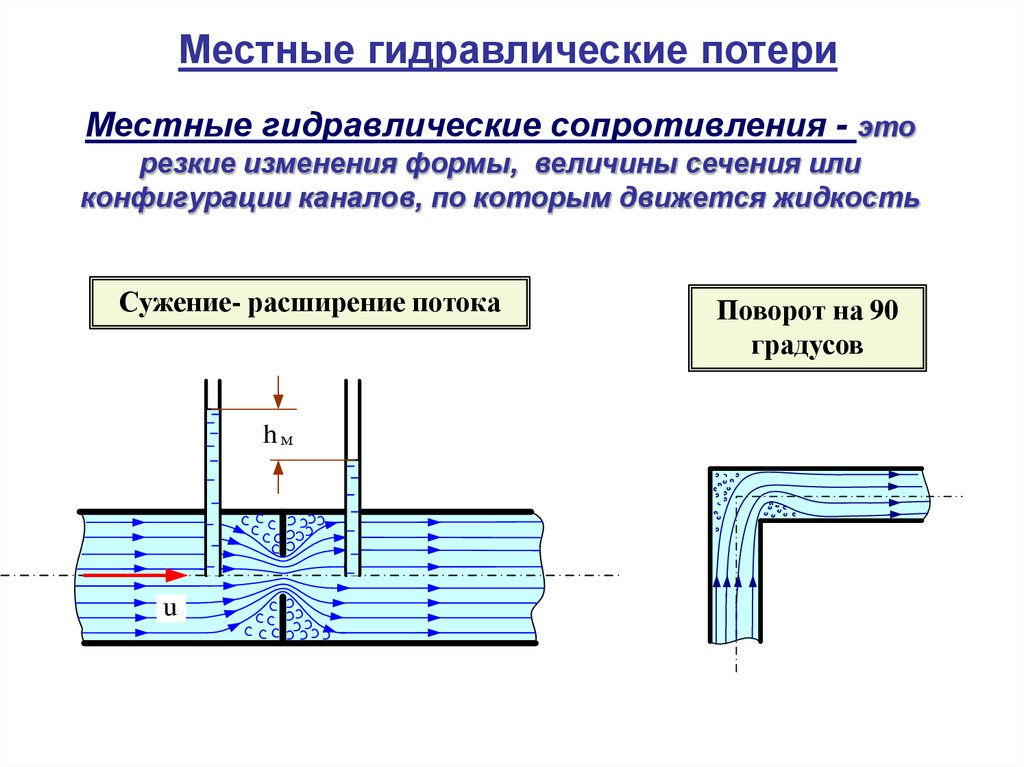
Местные гидравлические потериМестные гидравлические сопротивления - это
резкие изменения формы, величины сечения или
конфигурации каналов, по которым движется жидкость
Сужение- расширение потока
hм
u
Поворот на 90
градусов
30.
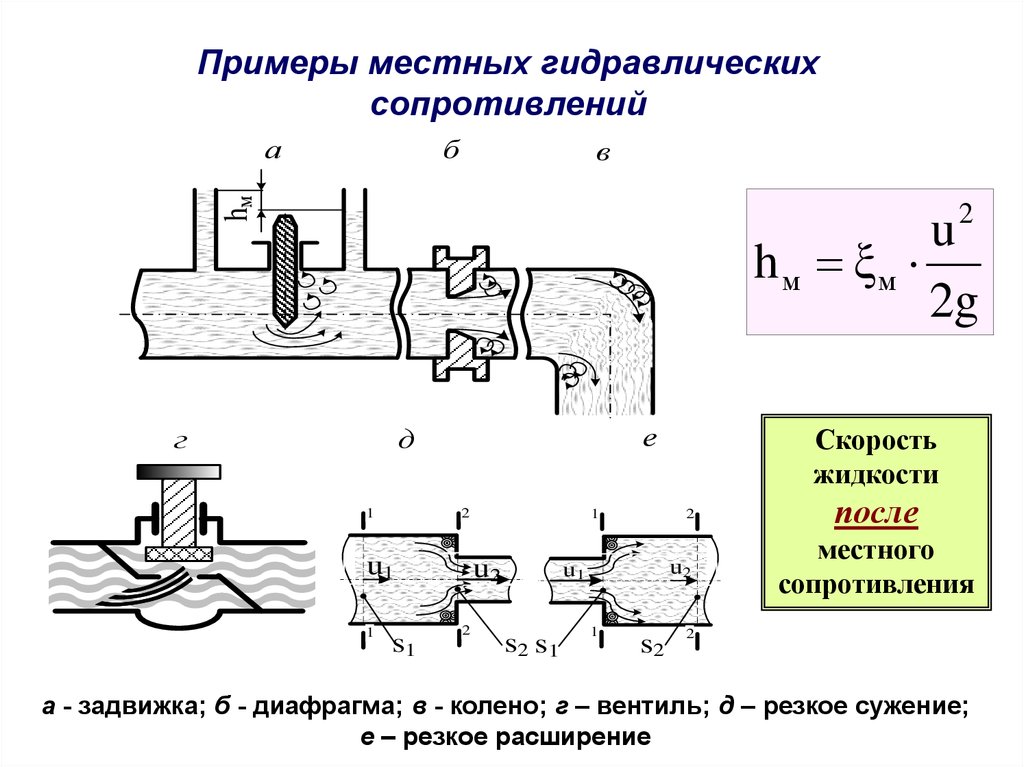
Примеры местных гидравлическихсопротивлений
б
в
hм
а
2
u
hм ξм
2g
е
д
г
1
2
u1
1
s1
1
u2
2
2
u2
u1
s2 s1
Скорость
жидкости
1
s2
после
местного
сопротивления
2
а - задвижка; б - диафрагма; в - колено; г – вентиль; д – резкое сужение;
е – резкое расширение
31.
Местное сопротивлениеВход в трубу:
при острых кромках
при закругленных кромках
u
Колено:
при R>2d
при R(3-7)d
d
0,5
0,3
R
Поворот под
прямым углом
Вентиль (при среднем
открытии)
Всасывающий клапан с сеткой
на входе в водопроводную
трубу
I,I
d
Задвижка на круглой
трубе:
полностью открытая
открыта на 3/4
открыта на 1/2
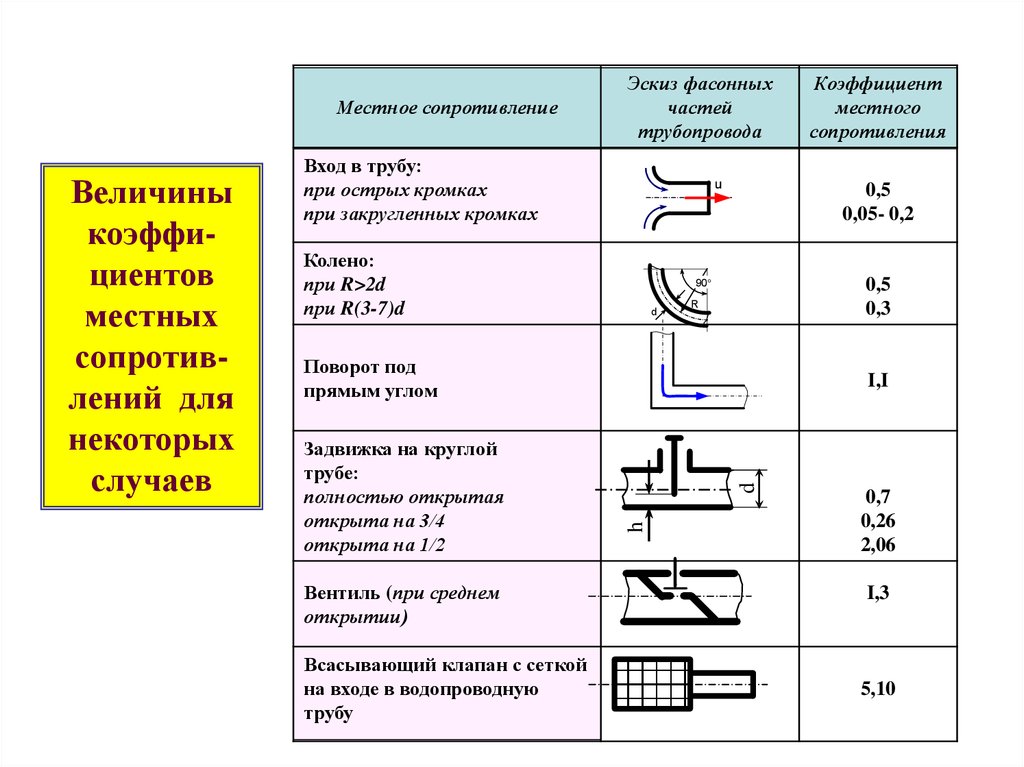
Коэффициент
местного
сопротивления
0,5
0,05- 0,2
90
h
Величины
коэффициентов
местных
сопротивлений для
некоторых
случаев
Эскиз фасонных
частей
трубопровода
0,7
0,26
2,06
I,3
5,10
32.
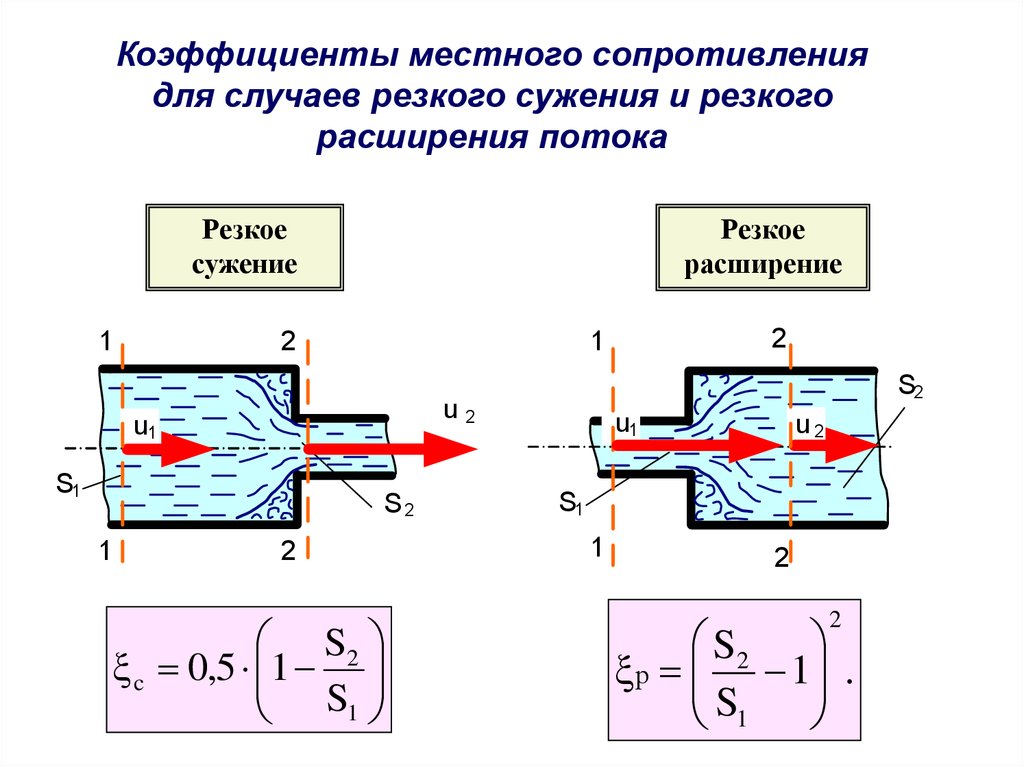
Коэффициенты местного сопротивлениядля случаев резкого сужения и резкого
расширения потока
Резкое
сужение
1
Резкое
расширение
2
S2
1
S2
u2
u1
S1
2
1
2
S2
c 0,5 1
S1
u1
u2
S1
1
2
2
S2
р 1 .
S1

















 Физика
Физика








