Похожие презентации:
Теориялық механика
1.
«Жалпы техникалық пәндер» кафедрасыф.-м.ғ.к., профессор Жоламанова Зауре Қамзақызы
2.
ПАЙДАЛАНЫЛАТЫН ӘДЕБИЕТТЕРӨ.А. Жолдасбеков, М.Н.Сағитов, К. Мустахишев. Теориялық
механика. А.: Мектеп, 1982. 1 бөлім
2. А. Түсіпов. Теориялық механика. А.: Дәуір, 2011.
3. С.Н.Тойбаев. Теориялық механика. А.: Бастау. 2006.
4. Сборник коротких задач по теоретической механике. Под
редакцией О.Э. Кепе. М.: Высшая школа, 1989г.
5. А. Түсіпов. Материалдар кедергісі. А:, 1991ж.
6. М.Рахымбекова. Материалдар кедергісі. А:, 1999ж.
7. Ш. А. Жолдасова, З.Қ. Жоламанова. Материлдар кедергісі. А:,
2007ж.
8. Под ред. Качурина В.К. Сборник задач по сопротивлению
материалов. М. : Н.1972г.
9. Винокуров А.И. Сборник задач по сопротивление материалов. М. :
Высш. шк., 1990г.
10. З.Қ . Жоламанова, Ш. А. Жолдасова. Материлдар кедергісі. Есептер
жинағы А: 2012ж.
1.
3.
Кіріспе. Негізгі түсініктер.Статика аксиомалары.
Байланыстар, байланыс
реакциялары
4.
МЕХАНИКА – механикалық қозғалыс туралы ғылым.Механикалық қозғалыс дегеніміз дененің уақыт озған
сайын кеңістіктегі орын ауыстыруын айтады.
Материалдық нүкте дегеніміз берілген есептің шартына
байланысты оның өлшемдерін ескермеуге болатын денені
айтады.
Абсолютты қатты дене деп қозғалыс кезінде кез-келген
екі нүктесінің арақашықтығы тұрақты болатын денені
айтады.
Механика
Қолданбалы механика
Теориялық механика
Ғимарат динамикасы
Құрылыс механикасы
Материалдар кедергісі
Корабль механикасы
Газ механикасы
Сұйық динамикасы
Құрылыс конструкциясы
Машин бөлшектері
Аспан механикасы
Грунт механикасы
Көпір мен тоннельдер
Машиналар мен механизмдер теориясы
Инженерлік механика
5.
ТЕОРИЯЛЫҚМЕХАНИКА
–
материялық
денелердің механикалық қозғалысының жалпы
заңдылықтары мен тепе-теңдігін және осы
материялық
денелердің
өзара
механикалық
әсерлесуін зерттейтін ғылым.
Теориялық механика үш бөлімге бөлінеді:
СТАТИКА – абсолют қатты денеге әсер ететін
күштер жүйесінің тепе теңдік шарттары зерттеледі.
КИНЕМАТИКА – әсер ететін күштер ескерілмей
қатты дене қозғалысының жалпы геометриялық
сипаттамалары зерттеледі
ДИНАМИКА – материялық нүктенің, қатты
дененің қозғалысы зерттелгенде, осы қозғалыстың
себебі болатын әсер етуші күштер ескеріледі.
6.
КҮШ – денелердің бір біріне өзара әсерлерінің сандықмөлшерімен анықталатын шама.
Күш векторлық шама, сондықтан ол үш көрсеткішпен
бейнеленеді:
1) F - модуль; 2) бағыты СД- әсер ету сызығы; 3) В түсу
нүктесі.
y
D
A
B
F
1 кГ 9,81Н 10Н,
C
1Н 0,102кГ 0,1кГ
x
7.
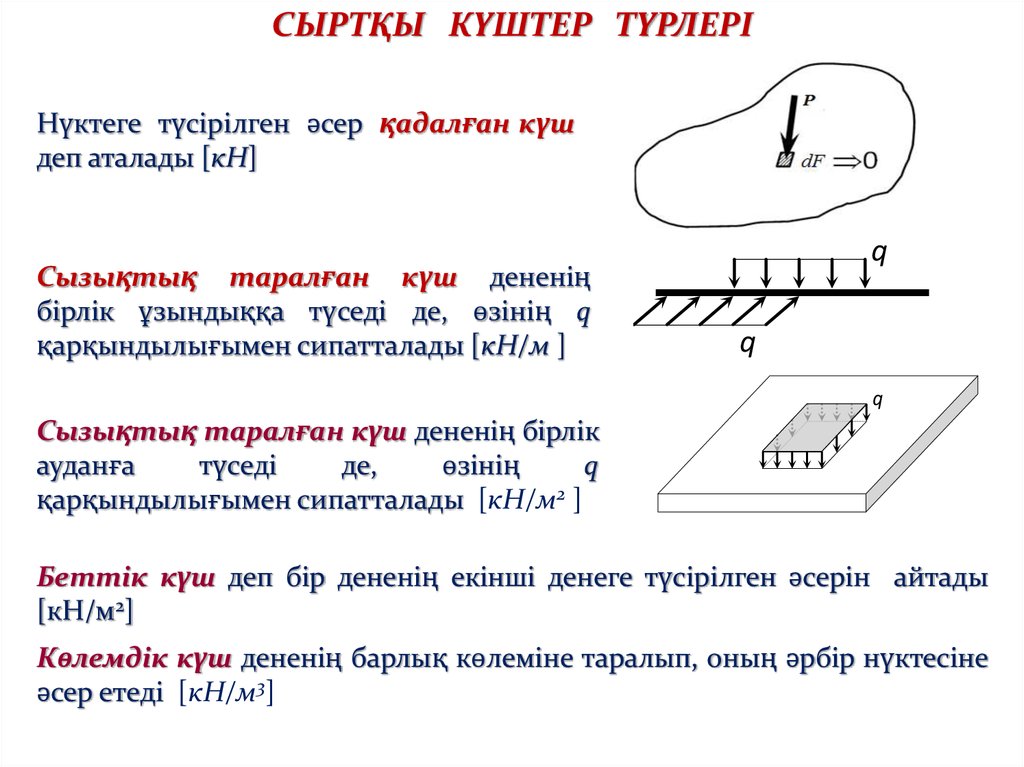
СЫРТҚЫ КҮШТЕР ТҮРЛЕРІНүктеге түсірілген әсер қадалған күш
деп аталады [кН]
Сызықтық таралған күш дененің
бірлік ұзындыққа түседі де, өзінің q
қарқындылығымен сипатталады [кН/м ]
q
q
q
Сызықтық таралған күш дененің бірлік
ауданға
түседі
де,
өзінің
q
қарқындылығымен сипатталады [кН/м2 ]
Беттік күш деп бір дененің екінші денеге түсірілген әсерін айтады
[кН/м2]
Көлемдік күш дененің барлық көлеміне таралып, оның әрбір нүктесіне
әсер етеді [кН/м3]
8.
КҮШТЕР АКСИОМАЛАРЫ1. Өзара теңескен күштер жүйесінің әсерінен дене тыныштық күйде
немесе бірқалыпты түзу сызықты қозғалыста болады.
F1
F2
F1 F2
2. Дененің бір нүктесіне түсірілген екі күштің тең әсер етуші күші сол
нүктеге
түсіріледі
де,
осы
күштерден
тұрғызылған
параллелограммның диогналымен анықталады.
F1
F1
F2
F2
R
R F1 F2
R F12 F12 2 F1 F2 cos( F1 , F2 )
9.
БАЙЛАНЫСТАР АКСИОМАСЫЕРКІН ДЕНЕ – кеңістіктің кез келген бағытында қозғала алатын дене
ЕРІКСІЗ ДЕНЕ – қозғалысы кеңістікте басқа бір немесе бірнеше денемен
шектелетін дене
БАЙЛАНЫСТАР – дененің орын ауыстыруын шектейтін шарттар
БАЙЛАНЫС РЕАКЦИЯСЫ – байланыс тарапынан қарсы әсер ететін күш
БАЙЛАНЫСТАН БОСАТУ АКСИОМАСЫ Кез келген еріксіз денені ойша
байланыстардан босатып және осы байланыстар әсерін сәйкес реакция
күштерімен алмастырсақ, онда еріксіз денені еркін дене деп
қарастыруға болады.
10.
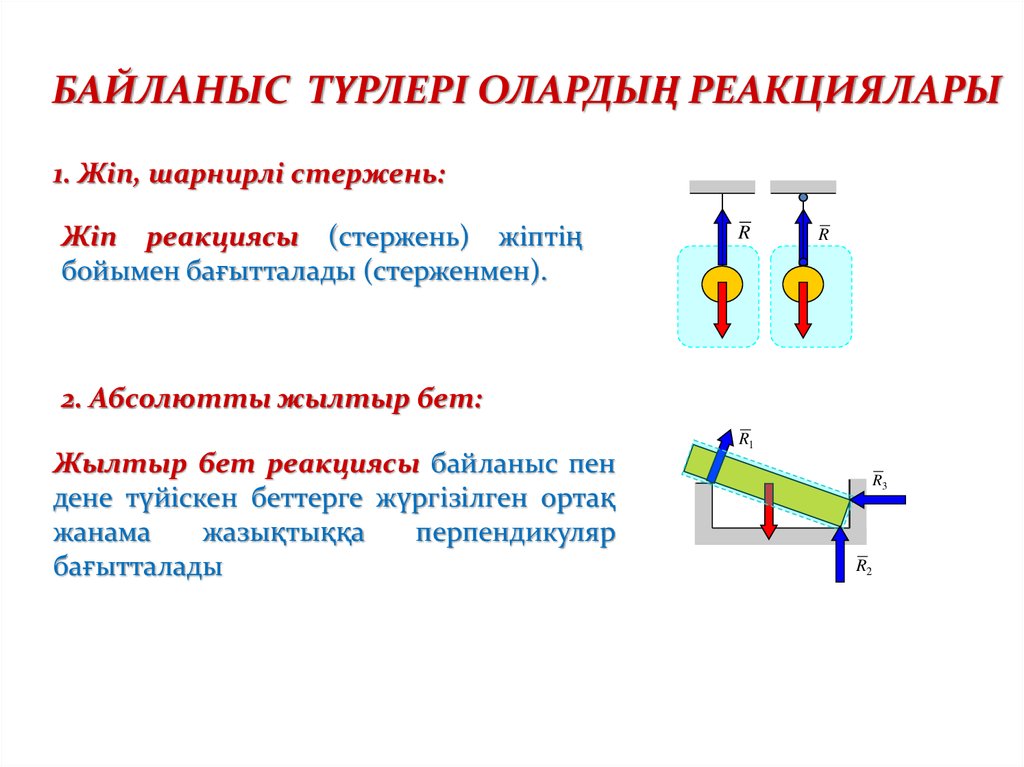
БАЙЛАНЫС ТҮРЛЕРІ ОЛАРДЫҢ РЕАКЦИЯЛАРЫ1. Жіп, шарнирлі стержень:
Жіп реакциясы (стержень) жіптің
бойымен бағытталады (стерженмен).
R
R
2. Абсолютты жылтыр бет:
Жылтыр бет реакциясы байланыс пен
дене түйіскен беттерге жүргізілген ортақ
жанама
жазықтыққа
перпендикуляр
бағытталады
R1
R3
R2
11.
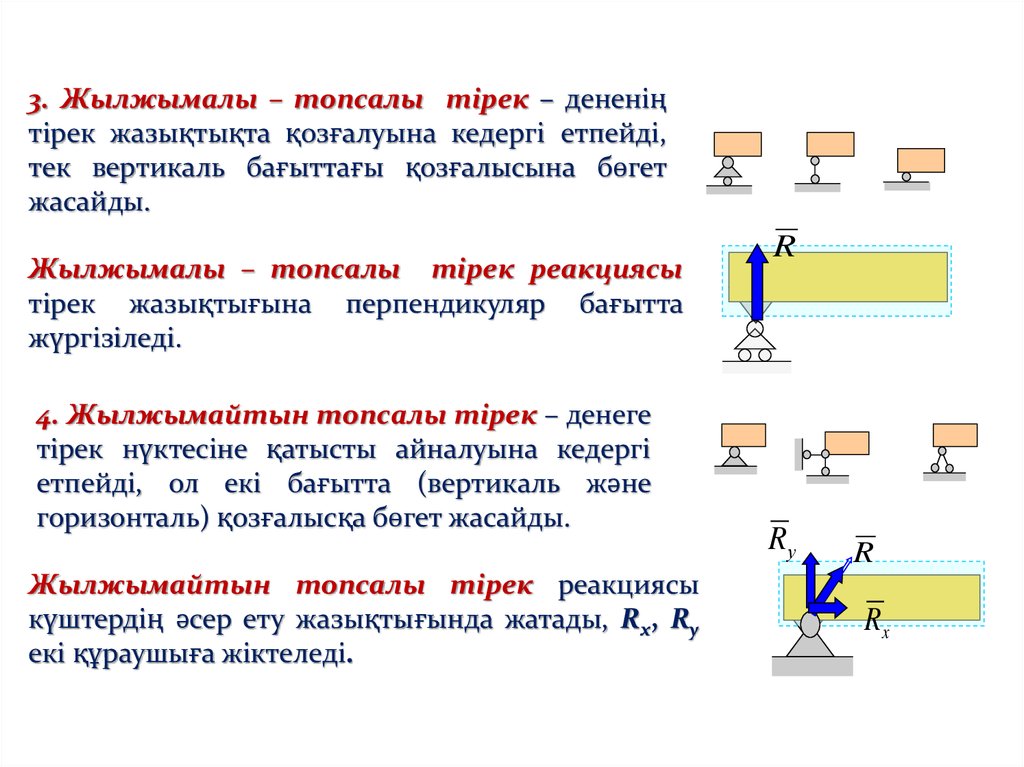
3. Жылжымалы – топсалы тірек – дененіңтірек жазықтықта қозғалуына кедергі етпейді,
тек вертикаль бағыттағы қозғалысына бөгет
жасайды.
Жылжымалы – топсалы тірек реакциясы
тірек жазықтығына перпендикуляр бағытта
жүргізіледі.
4. Жылжымайтын топсалы тірек – денеге
тірек нүктесіне қатысты айналуына кедергі
етпейді, ол екі бағытта (вертикаль және
горизонталь) қозғалысқа бөгет жасайды.
Жылжымайтын топсалы тірек реакциясы
күштердің әсер ету жазықтығында жатады, Rx, Ry
екі құраушыға жіктеледі.
R
Rу
R
Rx
12.
5. Қатаң бекітпе – дененің барлық қозғалуларына (бұрылуға жәнеекі бағытта қозғалуға) кедергі жасайды.
MA
R Ay
Жазық қатаң бекітпеде үш тірек
реакциясы анықталады: Rx, Ry
құраушы күш реакциялары және
бекітпе моменті.
екі
MA
R Ax
6. Жылжымайтын сфералық топса – дененің барлық
қозғалуларына (бұрылуға және екі бағытта қозғалуға) кедергі
жасайды.
Жылжымайтын сфералық топса
реакциясы топсаның центрі арқылы
өтіп, кеңістікте кез-келген бағытта
бағытталады: Rx, Ry, Rz үш құраушы күш
реакцияларына жүктеледі
R
13.
Бекітілу шартына байланысты келесі арқалық түрлерін ажыратылады:Консоль – бір жағы қатаң бекітпе, екінші жағы бос.
Қостіректі (жай арқалық)– екі жағы да топсалы тіректер.
Консольды арқалық– консольды бөліктері бар жай арқалық.
Құрама арқалық– екі және одан да көп консольды арқалықтан
құралған.
D
C
B
E
l
b
b
l
a
14.
ЖАЗЫҚ ЖИНАҚТАЛАТЫНКҮШТЕР СИСТЕМАСЫ. ТЕПЕТЕҢДІК ШАРТТАРЫ. КҮШ
МОМЕНТІ
15.
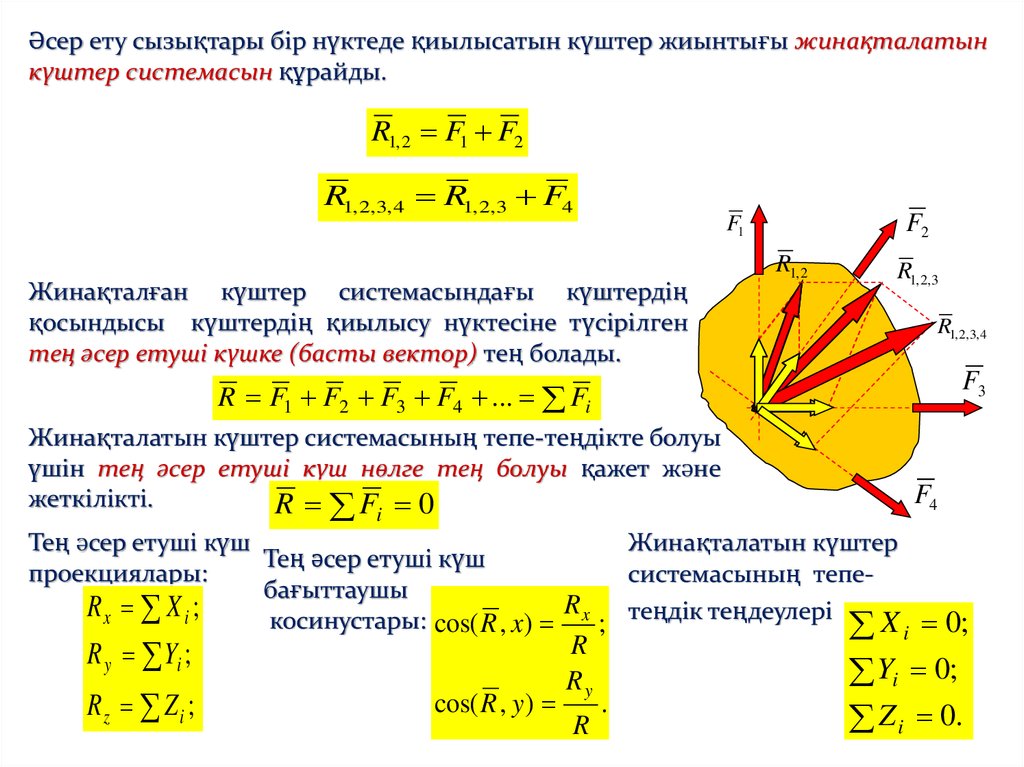
Әсер ету сызықтары бір нүктеде қиылысатын күштер жиынтығы жинақталатынкүштер системасын құрайды.
R1, 2 F1 F2
R1, 2,3, 4 R1, 2,3 F4
F2
F1
Жинақталған күштер системасындағы күштердің
қосындысы күштердің қиылысу нүктесіне түсірілген
тең әсер етуші күшке (басты вектор) тең болады.
R1, 2
R1, 2,3
R1, 2,3, 4
F3
R F1 F2 F3 F4 ... Fi
Жинақталатын күштер системасының тепе-теңдікте болуы
үшін тең әсер етуші күш нөлге тең болуы қажет және
жеткілікті.
R F 0
i
F4
Тең әсер етуші күш
Жинақталатын күштер
Тең әсер етуші күш
проекциялары:
системасының тепебағыттаушы
R
Rx X i ;
косинустары: cos( R , x) x ; теңдік теңдеулері X i 0;
R y Yi ;
Rz Z i ;
cos( R , y )
R
Ry
R
.
Yi 0;
Z i 0.
16.
Кез келген жазық күштер системасы – бір жазықтықта жататын жәнекүштің әсер ету сызықтары бір нүктеде қиылыспайтын күштер
системасы.
Осы күштер системасын қарастыру үшін келесі түсініктер енгізіледі:
1. Жазықтықтағы күштің нүктеге қатысты моменті.
2. Қос күш. Қос күш моменті.
Жазықтықтағы күштің нүктесіне қатысты моменті деп оң не теріс
таңбамен алынған күш модулі мен иінінің көбейтіндісіне тең скаляр
шаманы айтады. [Нм, кНм]. Күш иіні – нүктеден күш әсер ету сызығына
түсірілген перпендикуляр.
F
h
A
M A (F ) F h
Таңбалар ережесі:
Егер күш центрден денені сағат тілі бағытына
қарсы бағытта айналдыруға тырысса, онда
момент оң, ал сағат тілінің бағытымен бағыттас
айналдырса онда момент теріс.
Күштің нүктеге қатысты моментінің қасиеттері:
1) Егер де күш нөлге тең болса немесе оның әсер ету сызығы моменттің
центрі арқылы өтсе, онда күштің моменті нөлге тең болады;
2) Күштің түсу нүктесін, оның әсер ету сызығы бойымен
тасымалдағаннан күш моментінің шамасы өзгермейді.
17.
Қос күш – шамалары тең, бағыттары, қарама қарсы және әсер етусызықтары бір түзудің бойында жатпайтын параллель күштер жүйесі. Қос
күш тең әсер етуші күшке келтірілмейді. Қос күш әсерінен дене
айналысқа келтіріледі. Қос күш орналасқан жазықтықты қос күш әсер
жазықтығы, ал қос күштің әсер ету сызықтарының арасындағы ең
қысқа қашықтық h қос күш иіні деп аталады.
Жазықтағы қос күш моменті – деп оң не теріс таңбамен алынған қос
күштің кез-келген күш модулі мен қос күш иіні көбейтіндісіне тең скаляр
шаманы айтады .
F F
F
b
M A (F , F ) F (a b) F a Fb Fd
d
a
A
F
M A ( F , F ) F h
18.
ҚОС КҮШ ТЕОРЕМАЛАРЫҚос күшті қос күш әсер жазықтығында жылжыту туралы – қос
күшті өзінің әсер жазықтығының кез-келген нүктесіне тасымалдауға
болады.
Қос күш эквивалентілігі туралы – егер екі қос күш моменттерінің
алгебралық қосындысы тең болса, онда бір қос күшті екінші қос күшпен
алмастыруға болады
M ( F1 , F1 ) F1d1 , M ( F2 , F2 ) F2 d 2 ; F1d1 F2 d 2 ( F1 , F1 ) ( F2 , F2 )
Жазықтықтағы қос күштерді қосу туралы – қос күш системасын бір
қос күшке алмастыруға болады, оның моменті берілген қос күш
системасының моменттерінің алгебралық қосындысы тең болса
Қос күш тепе-теңдік шарты-
M Mi 0
19.
Берілген центрге (нүктеге) күшті келтіру (Пуансо тәсілі) – Дененің кезкелген нүктесіне түсірілген күшті шамасы мен бағыты дәл өзіндей дененің
басқа бір А нүктесіне түсірілген күшке және моменті берілген күштің А
нүктесіне қатысты моментіне тең қос күшке келтіруге болады.
F
M ( F , F )
F
d
F
A
А нүктесіне мәндері өзара бірдей, берілген
күштің шамасына тең, бағыттары бір
түзудің
бойында
қарама-қарсы
бағытталған, берілген кұшке параллель екі
күшті қосамыз:
F F F
Берілген
күш
пен
қарама-қарсы
бағытталған қосылған күштің біреуі қос
күшті құрайды.
Осы қос күш момент шамасы келтірілген центрге қатысты берілген
күштің моментіне тең болады.
M ( F , F ) F d F h M A ( F )
20.
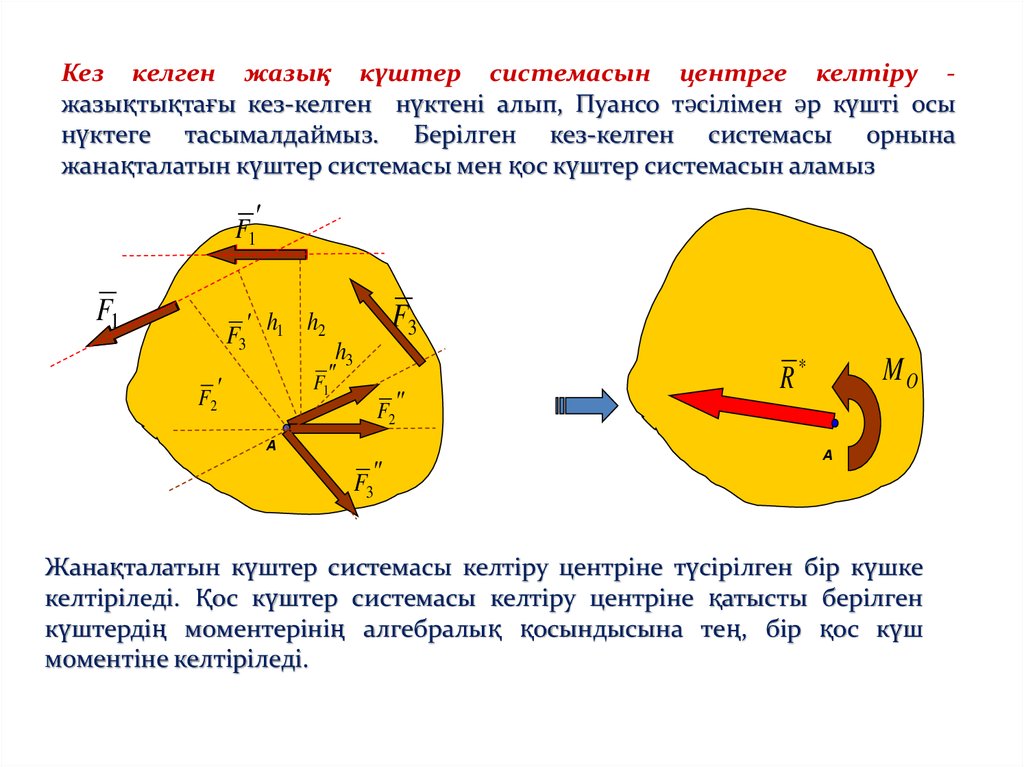
Кез келген жазық күштер системасын центрге келтіру жазықтықтағы кез-келген нүктені алып, Пуансо тәсілімен әр күшті осынүктеге тасымалдаймыз. Берілген кез-келген системасы орнына
жанақталатын күштер системасы мен қос күштер системасын аламыз
F1
F1
F3
F2
F3
h1 h2
h3
F1
F2
A
F3
MO
R*
A
Жанақталатын күштер системасы келтіру центріне түсірілген бір күшке
келтіріледі. Қос күштер системасы келтіру центріне қатысты берілген
күштердің моментерінің алгебралық қосындысына тең, бір қос күш
моментіне келтіріледі.
21.
Жалпы жағдайда кез-келген жазық күштер системасы бір бас векторге жәнебір бас моментке келтіріледі:
R * Fi
M M A M iA
Кез-келген жазық күштер системасының тепе-теңдік шарттары:
R * Fi 0
M M A M iA 0
Тепе-теңдік теңдерлер (I түрі) :
Тепе-теңдік теңдерлер (II түрі) :
Тепе-теңдік теңдерлер (III түрі) :
X i 0;
Yi 0;
M iA 0
X i 0;
M iB 0;
M iA 0
M iC 0;
M iB 0;
M iA 0
Тепе-теңдік
теңдерлерін
(II не III) құрғанда х
өсіне
(AB
перпендикуляр емес)
және С нүктесіне (AB
түзуінде жатпайды)
шарт қойылады
22.
МАТЕРИАЛДАР КЕДЕРГІСІ:НЕГІЗГІ ТҮСІНІКТЕР.
ПӘННІҢ МАҚСАТЫ.
НЕГІЗГІ ГИПОТЕЗАЛАР.
ДЕНЕНІҢ ТҮРЛЕРІ
23.
Материалдар кедергісі дегеніміз беріктілік, орнықтылықжәне төзімділік туралы ғылым
Беріктік дегеніміз дененің немесе конструкция
элементінің
сыртқы күш әсеріне сынбай, қирамай
қарсыласу қабілеті.
Қатаңдық дегеніміз дененің деформацияға қарсыласу
қабілеті.
Орнықтылық дегеніміз дененің сыртқы күш әсеріне
өзінің тепе-теңдігін жоғалтпай қарсыласу қабілеті
МАТЕРИАЛДАР КЕДЕРГІСІ МАҚСАТЫ – салмағы
жағынан жеңіл, қатаңдығы мен беріктігі жоғары, өзі арзан
конструкциялардың жобасын есептеу болып табылады.
24. МАТЕРИАЛДАР КЕДЕРГІСІНДЕ ҚОЛДАНЫЛАТЫН ГИПОТЕЗАЛАР • БІРТЕКТІЛІК • БІР ТҰТАСТЫҚ • ИЗОТРОПТЫЛЫҚ • СЕРПІМДІЛІК
25.
Материалдар құрамы БІРТЕКТІ, яғни дененің қайжерінде болмасын, оның қасиеттері бірдей.
Дененің құрамы БІРТҰТАС, себебі дене затпен
толық толтырылған, ешбір қуысы жоқ.
Конструкцияда
қолданылатын
барлық
материалдар ИЗОТРОПТЫ, демек, дененің әр
нүктесіндегі қасиеттері барлық бағытта бірдей.
Материалдардың
барлығы
да
түбегейлі
СЕРПІМДІ, демек, денеге әсер еткен күш алып
тасталса, ол дене бастапқы қалпына қайтып
келеді.
26.
ДЕНЕ КАТЕГОРИЯСЫb
СЫРЫҚ деп бір өлшемі қалған екеуіне
қарағанда анағұрлым үлкен денелерді
айтады l>>a, b. (білік, стержень, арқалық,
бағана)
l
a
Сырық өсі деп сырықтың көлденең
қималарының ауырлық центрі арқылы
өтетін сызықты айтады
27.
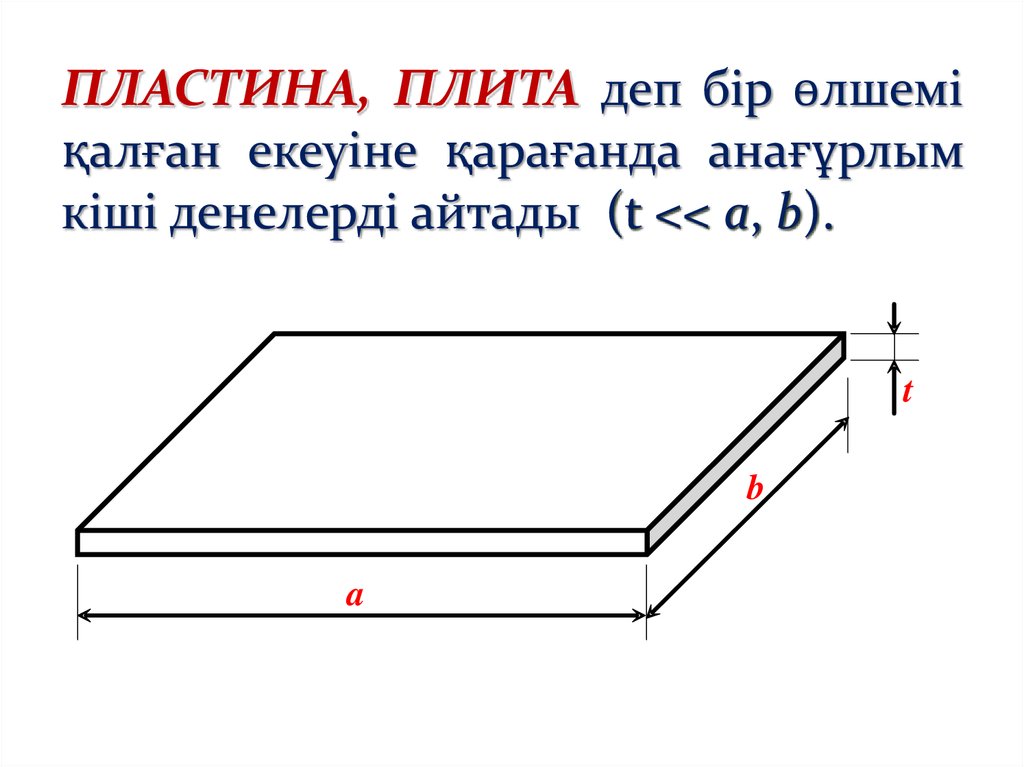
ПЛАСТИНА, ПЛИТА деп бір өлшеміқалған екеуіне қарағанда анағұрлым
кіші денелерді айтады (t << a, b).
t
b
a
28.
ҚАБЫРШАҚ - қалыңдығыөлшемдерінен
кіші
екі
беттермен шектелген дене
қалған
қисық
t
b
a
29.
МАССИВ деп үш өлшемі де біршамалас денелерді айтады (a≈b≈c).
c
b
a
30.
ІШКІ КҮШТЕР. ҚИМАТӘСІЛІ. НЕГІЗГІ
ТҮСІНІКТЕР: КЕРНЕУ,
ДЕФОРМАЦИЯ
31.
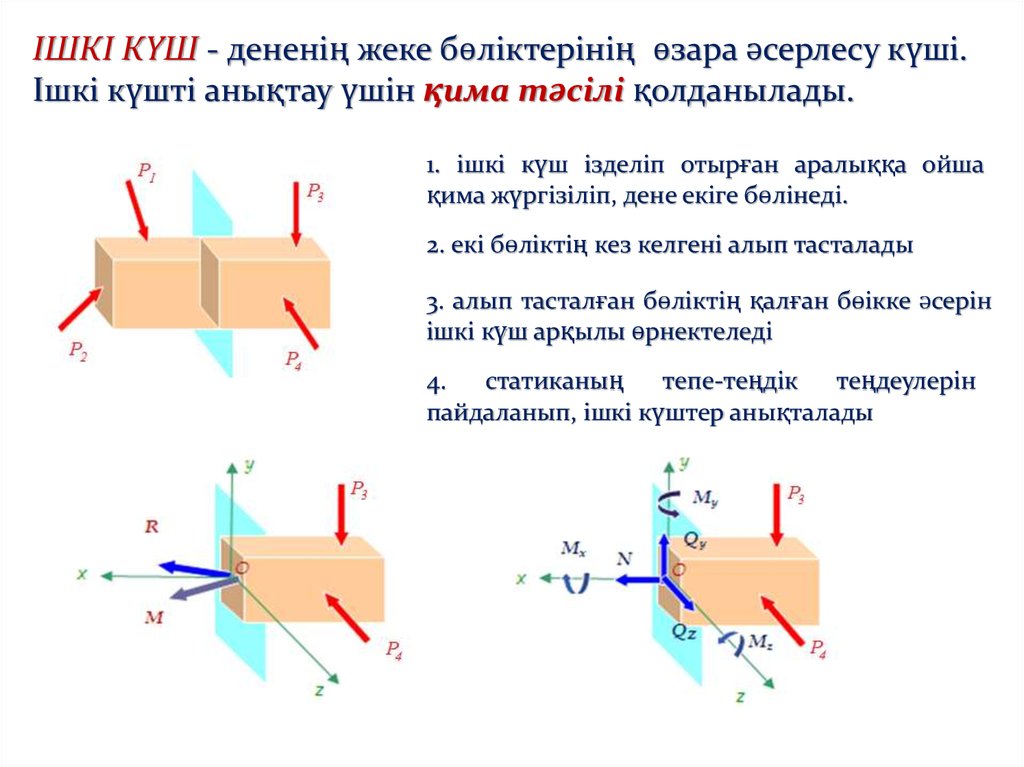
ІШКІ КҮШ - дененің жеке бөліктерінің өзара әсерлесу күші.Ішкі күшті анықтау үшін қима тәсілі қолданылады.
1. ішкі күш ізделіп отырған аралыққа ойша
қима жүргізіліп, дене екіге бөлінеді.
2. екі бөліктің кез келгені алып тасталады
3. алып тасталған бөліктің қалған бөікке әсерін
ішкі күш арқылы өрнектеледі
4.
статиканың
тепе-теңдік теңдеулерін
пайдаланып, ішкі күштер анықталады
32.
Ішкі күштер құраушылары ІШКІ КҮШ ФАКТОРЛАРЫ(ІКФ) деп аталады да, олардың материалдар кедергісінде
арнайы атаулары бар:
N – бойлық күш,
Qz, Qy – көлденең күштер,
Mx – бұралу момент,
Mz, My – иілу моменттер.
N Рхi ; M x M xi ;
к.б.
к.б.
Q y Р уi ; M y M уi ;
к.б.
Qz Рzi
к.б.
к.б.
; M z M zi .
к.б.
33.
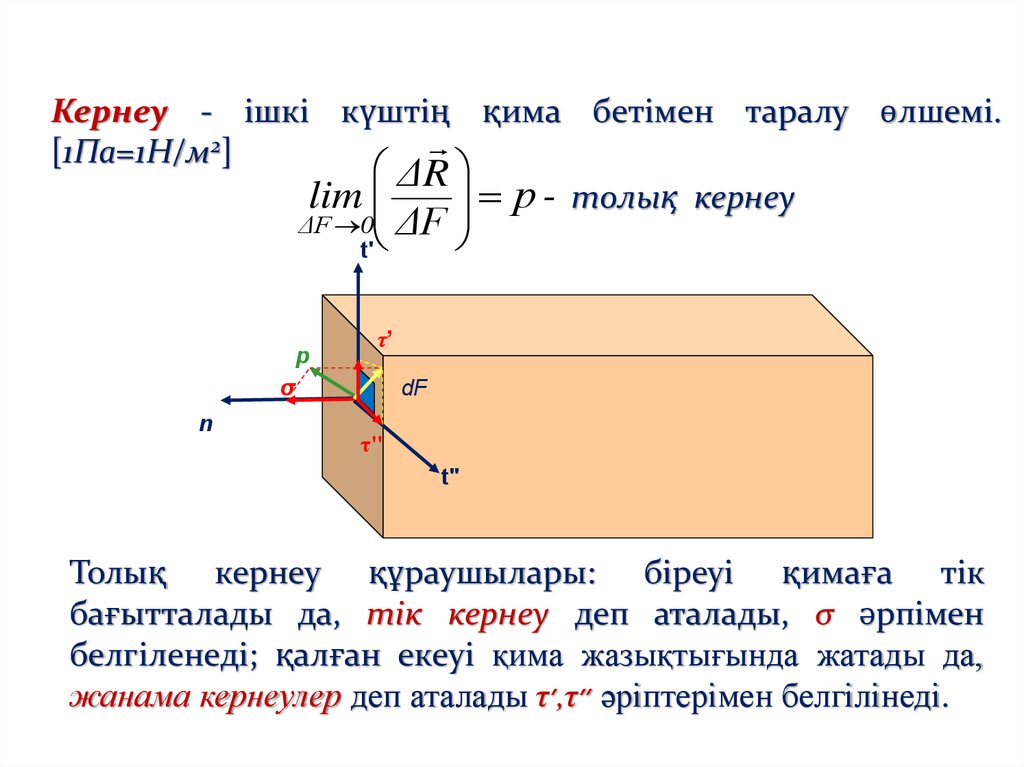
Кернеу - ішкі күштің қима бетімен таралу өлшемі.[1Па=1Н/м2]
ΔR
р - толық кернеу
lim
ΔF 0 ΔF
t'
p
τ’
σ
n
dF
τ"
t"
Толық кернеу құраушылары: біреуі қимаға тік
бағытталады да, тік кернеу деп аталады, σ әрпімен
белгіленеді; қалған екеуі қима жазықтығында жатады да,
жанама кернеулер деп аталады τ׳,τ ״әріптерімен белгілінеді.
34.
ІШКІ КҮШ ФАКТОРЛАРЫ МЕНКЕРНЕУ АРАСЫНДАҒЫ ТӘУЕЛДІЛІКТЕР
Нүктеден өтетін сан алуан жазықтықтағы тік және жанама
кернеулердің
жиынтығы
нүктенің
кернеулі
күйін
сипаттайды
N x dF ;
F
Qy xy dF ;
F
Qz zx dF .
M x ( xy x zx y)dF ;
F
M z x ydF ;
F
M y x zdF .
F
F
Ішкі
күш
факторларының дененің ұзындығы
бойынша өзгерісін көрсететін графикті ІКФ эпюрі деп
аталады.
35.
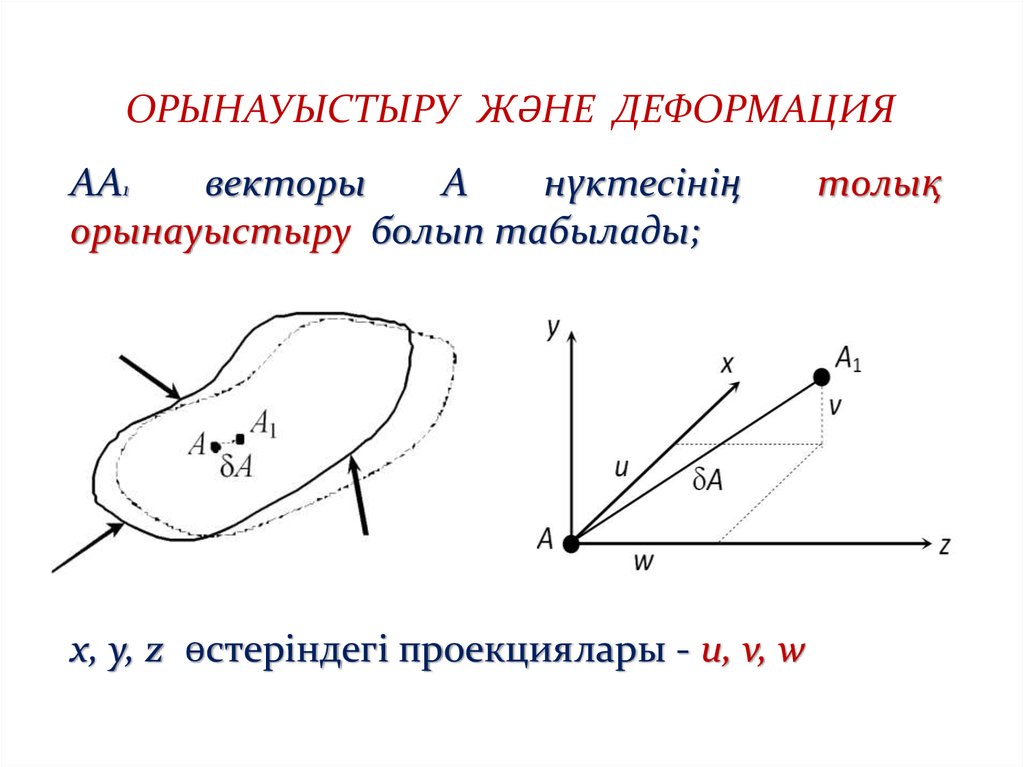
ОРЫНАУЫСТЫРУ ЖӘНЕ ДЕФОРМАЦИЯАА1
векторы
А
нүктесінің
орынауыстыру болып табылады;
x, y, z өстеріндегі проекциялары - u, v, w
толық
36.
Деформация – сыртқы күш әсерінен дене пішіні мен көлемініңөзгерісі.
Δ
S
lim
ε
S
ΔS 0
ε - сызықтық деформация;
x, y, z
өстеріндегі
проекциялары - x , y , z
Егер А, В нүктелерінің аралығы ұлғайса, онда салыстырмалы
ұзару, ал азайса - салыстырмалы қысқару делінеді.
lim
АВ 0,АС 0
( ВАС В1 А1С1 ) γ
γ - бұрыштық деформация; x, y, z өстеріндегі проекциялары xy , xz , yz
37.
ҚАРАПАЙЫМ ДЕФОРМАЦИЯТҮРЛЕРІ
-Созылу– сығылу
-Ығысу
-Бұралу
- Иілу(таза, көлденең)
38.
ЖАЗЫҚ ҚИМАНЫҢГЕОМЕТРИЯЛЫҚ
СИПАТТАМАЛАРЫ:
СТАТИКАЛЫҚ МОМЕНТ,
ИНЕРЦИЯ МОМЕНТІ
39.
Созылу-сығылудағы кернеуді анықтауда негізгі геометриялық сипаттамасырықтың ауданы болып табылады. Ал бұралудағы, иілудегі кернеуді анықтау
үшін келесі геометриялық сипаттама қолданылады.
Көлденең қиманың ауданы:
y
F dF
х
[см2, м2]
F
Қиманың статикалық моменті
dF
S x ydF ; S y xdF [см3, м3]
F
F
Қиманың өстік инерция моменттері
у
I x y 2 dF ;
x
I y x 2dF [см4, м4]
F
O
F
Қиманың центрден тепкіш инерция моменті
I xy xydF
Қиманың полярлық инерция моменті
I ρ ρ 2 dF (x 2 y 2 )dF I y I x
F
F
Қиманың полярлық
моменттері қосындысына тең.
Тұжырым:
[см4, м4]
F
[см4, м4]
инерция
моменті
өстік
инерция
40.
Статикалық моменті нолге (Sx=0, Sy=0) тең өстер орталық өстер депаталады.
Орталық өстердің өзара қиылысу нүктесі, қиманың ауырлық центрі
болып табылады
Күрделі қиманың ауырлық центрін анықтау үшін :
1. Кезкелген (бастапқы) x, y координат өстерін таңдау керек;
2. Берілген күрделі қиманы қарапайым қималарға бөлу қажет.
3. Келесі формулаларды пайдаланып, қиманың ауырлық центрінің
координатасын есептеу керек.
n
xС
Sy
Fi xi
i 1n
,
F
Fi
i 1
n
Fi yi
S x i
yС
1n
F
Fi
i 1
Тұжырым: егер қиманың өстерінің біреуі немесе екеуі де қиманың
симметрия өсімен сәйкес келсе, онда осы өстерге қатысты қиманың
центрден тепкіш инерция моменті нөлге тең болады
I xy 0
41.
КООРДИНАТ ӨСТЕРІН ПАРАЛЛЕЛЬ ЖЫЛЖЫТҚАНДАГЕОМЕТРИЯЛЫҚ СИПАТТАМАЛАРДЫҢ ӨЗГЕРІСІ
жаңа координаталар: х 1 = x +b, y 1 =y+a
y
y1
S x1 y1dF (y a)dF S x aF
F
x1
O
x
b
I x1 y12 dF I x 2aS x a 2 F
F
x1
x
1
Тұжырым: статикалық момент - аудан мен
өстер
жылжыған
ара
қашықтық
көбейтіндісіне тең шамаға өзгереді
y
a
O1
S y S y bF
y1 өсіне сәйкес:
dF
y1
F
y1 өсіне сәйкес : I y I y 2bSy b 2 F
1
Ix
y
1 1
y1 x1 dF (y a)(x b)dF I xy aS y bSx abF
F
F
Егер х, у орталық өстер болса, яғни Sx = Sy = 0:
I x I x a 2 F, I y I y b 2 F
1
1
Ix
y
1 1
I xy abF
Тұжырым: өстік инерция моменті - аудан мен өстер (олардың біреуі-орталық)
жылжыған ара қашықтықтың квадратының көбейтіндісіне тең шамаға, ал
центрден тепкіш инерция моменті - аудан мен өстер жылжыған ара
қашықтықтардың көбейтіндісіне тең шамаға өзгереді
42.
КООРДИНАТ ӨСТЕРІН БҰРҒАНДА ИНЕРЦИЯМОМЕНТТЕРІНІҢ ӨЗГЕРІСІ
u=xcosα+ysinα,
жаңа координаталар:
v=-xsinα+ycosα
y
dF
u
v
u
y
v
I u v 2 dF (ycos xsin )2 dF
F
F
I x cos 2α I y sin 2α I xy sin2α.
O1
u өсіне қатысты өстік инерция моменттері:
x
v өсіне сәйкес:
I v I x sin 2α I y cos 2α I xy sin2α.
I u I v I x I y const
x
Тұжырым: өзара перпендикуляр екі өстердегі инерция моменттерінің қосындысы
α бұрышына тәуелді болмайды.
u және v өстеріне қатысты центрден тепкіш инерция моменті:
I uv uvdF (ysin xcos )(ycos хsin )dF
F
F
Ix I y
sin2α I xy cos2
2
43.
Центрден тепкіш инерция моменті нольге тең, ал өстік инерциямоменттері экстремаль шамаға ие болатын өстер бас өстер деп аталады.
Қиманың ауырлық центрі арқылы өтетін бас өстер орталық бас инерция
өстері деп аталады. Бас өстердегі өстік инерция моменттері бас инерция
моменттері болып табылады.
2I xy
Бас өстердің орнын анықтау формуласы:
tg2α
1
cosα
,
2
1 tg 2α
tg 2 2α
sinα
1 tg 2 2α
1 cos2α
1 cos2α
2
cos α
, sin α
2
2
2
БАС ИНЕРЦИЯ МОМЕНТТЕРІ :
I u, v
Ix I y 1
2
2
I x I 2 4I xy2
y
Iy Ix
44.
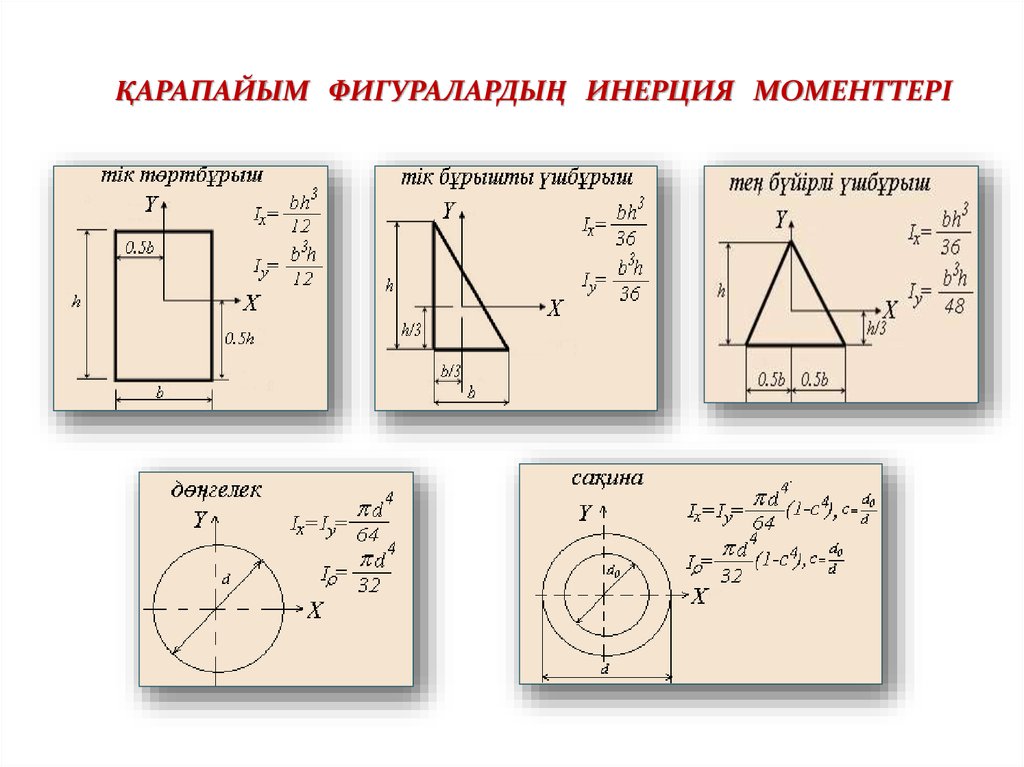
ҚАРАПАЙЫМ ФИГУРАЛАРДЫҢ ИНЕРЦИЯ МОМЕНТТЕРІ45.
СОЗЫЛУ-СЫҒЫЛУ. КЕРНЕУМӘНІ. ГУК ЗАҢЫ. БОЙЛЫҚ,
КӨЛДЕНЕҢ ДЕФОРМАЦИЯ.
БЕРІКТІК ШАРТЫ
46.
Сыртқы күш әсерінен сырықтың көлденең қимасында текқана N бойлық күш пайда болатын деформация түрі
созылу немесе сығылу деп аталады.
N таңбалар ережесі :
Егерде қима жағынан қарағанда
сыртқы күш қалған бөлікті созса,
онда осы қимадағы бойлық күш оң
таңбалы және керісінше.
N эпюрасы ерешеліктер
1.
Егер сырық тұрақты сыртқы күшпен жүктелсе, онда N
эпюрасында осы күш түскен нүктеде күшке тең секіріс
болады.
2. Сырықтың көлденең қимасының өзгерісі N эпюрасына
әсерін тигізбейді.
3. Егер сырық таралған күшпен жүктелсе, онда N эпюрасы
осы таралған күштің таралу ұзындығында көлбеу түзу
сызықпен шектеледі.
47.
Созылу-сығылудағы кернеулік күйді анықтау үшінкелесі гипотезалар қолданылады:
ЖАЗЫҚ ҚИМАЛАР ГИПОТЕЗАСЫ
(Бернулли гипотезасы)
Деформацияға
дейінгі
жазық
қималар деформациядан кейін де
жазық күйінде қалады.
48.
СЕН-ВЕНАН ГИПОТЕЗАСЫСырықтың бекітілуінің және оған әсер
етіп тұрған күштердің ерекшеліктері,
әдетте,
осы
сырықтың
көлденең
қимасының негізгі өлшемінен аспайтын
арақашықта ғана байқалады.
49.
Созылу-сығылу кезінде көлденең қимадатек қана тік кернеу σ пайда болады.
Бернулли
гипотезасы
бойынша
қимадағы тік кернеулер бір қалыпты
таралады, яғни,
N
σ
F
Кернеу мен деформация арасындағы тәуелділік Гук заңы:
Серпімділік шеңберінде материалдардың басым көпшілігінің
кернеулері деформациялармен пропорционалдық қатынаста
болады.
Е
E – пропорциональдық коэффициенті; серпімділік модулінің I түрі [Па].
ε – бойлық деформация [өлшемсіз
шама]
50.
Бойлық деформацияабсолютті бойлық деформация
(толық ұзару)
Δl l l0
бойлық деформация (салыстырмалы
ұзару)
Δ
ε
0
Көлденең деформация
абсолютті көлденең деформация
Δa a a1
көлденең деформация
ε Δa
a
Пуассон коэффициенті
ε
ε
μ
μ 0,02 0,5
51.
Сырықтық абсолютті бойлық деформациясы (толықұзару) бойлық күш арқылы анықталады:
l l
l
E
Nl
l
EF
EF – созылу-сығылудағы сырықтың қатаңдығы
Толық ұзарудың температураға байланысты өзгерісі
N
Δ
α Δt
EF
α
–
материалдың
коэффициенті;
Δt
температуралық
- дене температурасының өзгеру шамасы
ұлғаю
52.
БЕРІКТІК ШАРТЫМатериалдар кедергісінің негізгі есебі – әртүрлі жүктемелердің
әсерінен конструкция және оның элементтерінің сенімді өлшемдерін
қамтамасыз ету. Созылу-сығылудағы беріктік шарт :
σ max
σ -
N max
F
сырық материалының мүмкін кернеуі
ЕСЕПТЕУ ТҮРЛЕРІ
1. Тексеру есебі: беріктікті тексеру
Кернеудің есептеу мәні
қабылданады.
σ max σ
мүмкін кернеуден 5
%
артық мәні
2. Жобалау есебі:
қиманы таңдау. Конструкция элементерінің
N max
көлденең қимасының геометриялық өлшемін анықтау
.
F
3. Жүктелуді есептеу: мүмкін күшті анықтау.
[ N ] F[ ]
σ
53.
ПОТЕНЦИЯЛЫҚ ЭНЕРГИЯСерпімді денеге түсірілген сыртқы күштер, дененің
пішінін өзгертіп, қандай да бір А жұмыс жасайды, яғни
денеде деформацияның потенциялық энергиясы пайда
болады Энергияның сақталу заңына сүйенсек, дененің
формасын
өзгертетін
жұмыс,
сол
дененің
деформациясының
U
потенциялық
энергиясына
айналады.
1
А U; U N Δl;
2
Созылу-сығылудағы потенциялық энергия
2l
N
U
2EF
54.
55.
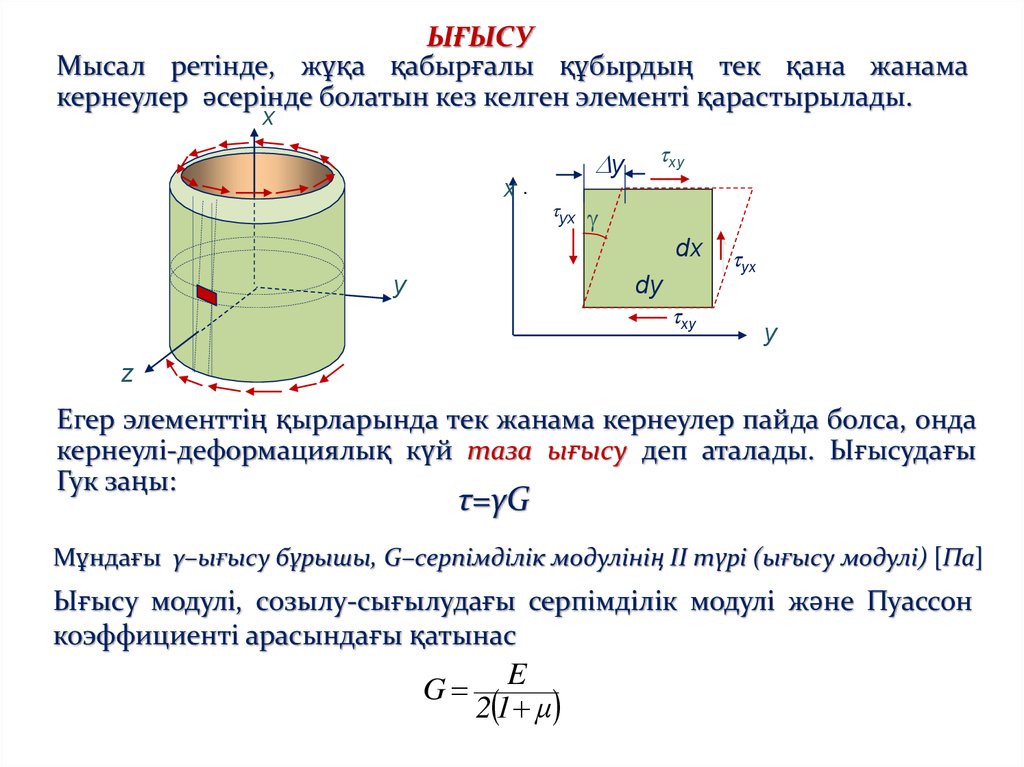
ЫҒЫСУМысал ретінде, жұқа қабырғалы құбырдың тек қана жанама
кернеулер әсерінде болатын кез келген элементі қарастырылады.
x
x.
y
yх
хy
dх
y
dy
хy
yх
y
z
Егер элементтің қырларында тек жанама кернеулер пайда болса, онда
кернеулі-деформациялық күй таза ығысу деп аталады. Ығысудағы
Гук заңы:
τ=γG
Мұндағы γ–ығысу бұрышы, G–серпімділік модулінің II түрі (ығысу модулі) [Па]
Ығысу модулі, созылу-сығылудағы серпімділік модулі және Пуассон
коэффициенті арасындағы қатынас
G
E
2 1 μ
56.
Бұралуға жұмыс істейтін сырық білік немесе білеу деп аталады.Сыртқы жүктеме әсерінен біліктің көлденең қимасында тек қана
Мб бұралу моменті пайда болатын деформация түрі бұралу деп
аталады.
Мб таңбалар ережесі
егер қима жағынан қарағанда сыртқы
момент қалған бөлікті сағат тілімен
бағыттас бұраса, онда осы қимадағы
бұралу моменті оң таңбалы және
керісінше.
1.Егер білік тұрақты сыртқы моментпен жүктелсе, онда Мб эпюрасында
осы момент түскен нүктеде моментке тең секіріс болады.
2.Біліктің көлденең қимасының өзгерісі Мб эпюрасына әсерін
тигізбейді.
3.Егер білік таралған моментпен жүктелсе, онда Мб эпюрасы осы
таралған моменттің таралу ұзындығында көлбеу түзу сызықпен
шектеледі.
57.
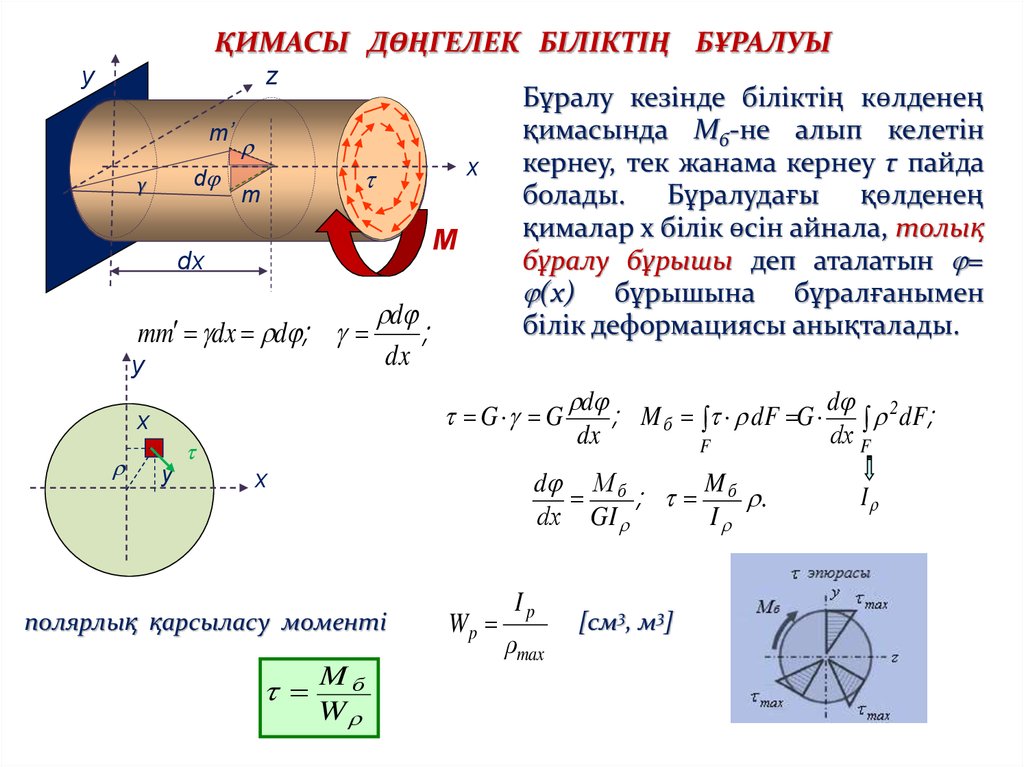
ҚИМАСЫ ДӨҢГЕЛЕК БІЛІКТІҢ БҰРАЛУЫy
z
d
γ
x
m’
m
M
dx
mm dx d ;
y
d
;
dx
G G
x
Бұралу кезінде біліктің көлденең
қимасында Mб-не алып келетін
кернеу, тек жанама кернеу τ пайда
болады. Бұралудағы қөлденең
қималар х білік өсін айнала, толық
бұралу бұрышы деп аталатын =
(х) бұрышына бұралғанымен
білік деформациясы анықталады.
y
M
d М б
; б .
dх GI
I
x
полярлық қарсыласу моменті
d
d
; M б dF G 2 dF;
dx
dх F
F
Mб
W
Wp
Ip
ρmax
[см3, м3]
I
58.
ҚИМАНЫҢ ГЕОМЕТРИЯЛЫҚ СИПАТТАМАЛАРЫНАНЫҚТАУ ФОРМУЛАЛАРЫ
Дөңгелек :
y
D
πR 4 πd 4
Iρ
0,1d 4 ,
2
32
πR 3 πd 3
Wρ
0,2d 3 .
2
16
dρ
x
Сақина
y
D
d
π(R4 r 4 ) π(D4 d 4 )
Iρ
0,1D4 1 к 4 ,
2
32
dρ
x
π(R3 r 3 ) π(D3 d 3 )
d
Wρ
0,2D3 1 к 4 , k
2
16
D
59.
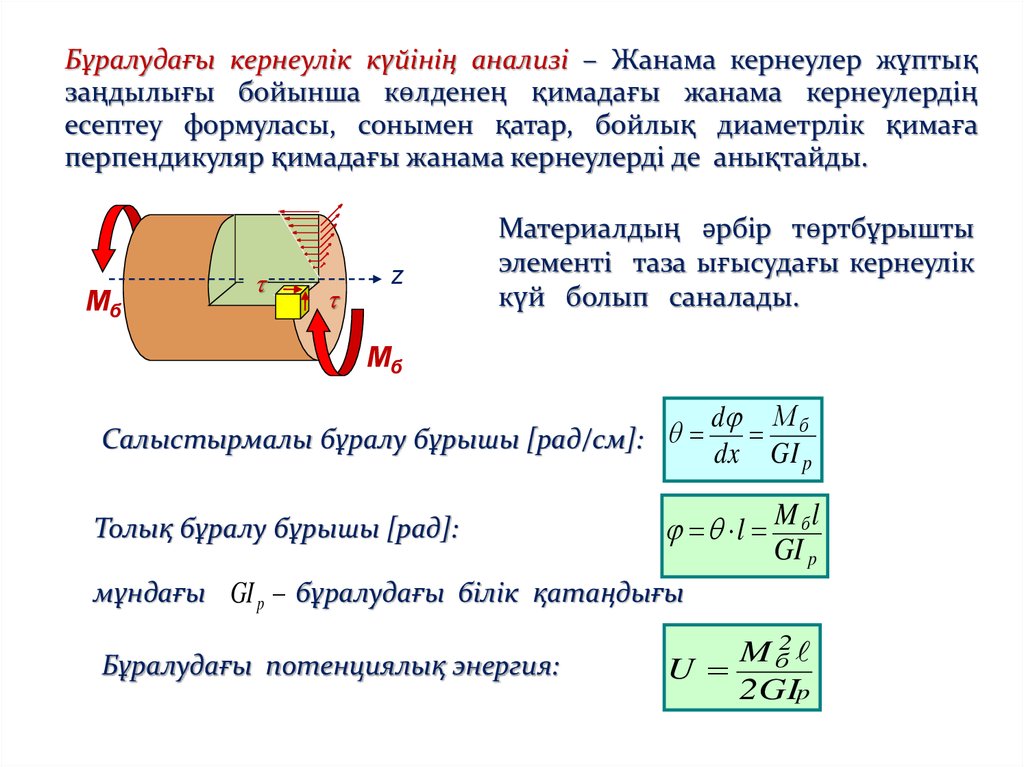
Бұралудағы кернеулік күйінің анализі – Жанама кернеулер жұптықзаңдылығы бойынша көлденең қимадағы жанама кернеулердің
есептеу формуласы, сонымен қатар, бойлық диаметрлік қимаға
перпендикуляр қимадағы жанама кернеулерді де анықтайды.
Mб
z
Материалдың әрбір төртбұрышты
элементі таза ығысудағы кернеулік
күй болып саналады.
Mб
d М б
Салыстырмалы бұралу бұрышы [рад/см]:
dx GI p
Толық бұралу бұрышы [рад]:
l M бl
GI p
мұндағы GI p бұралудағы білік қатаңдығы
Бұралудағы потенциялық энергия:
M б2
U
2GIp
60.
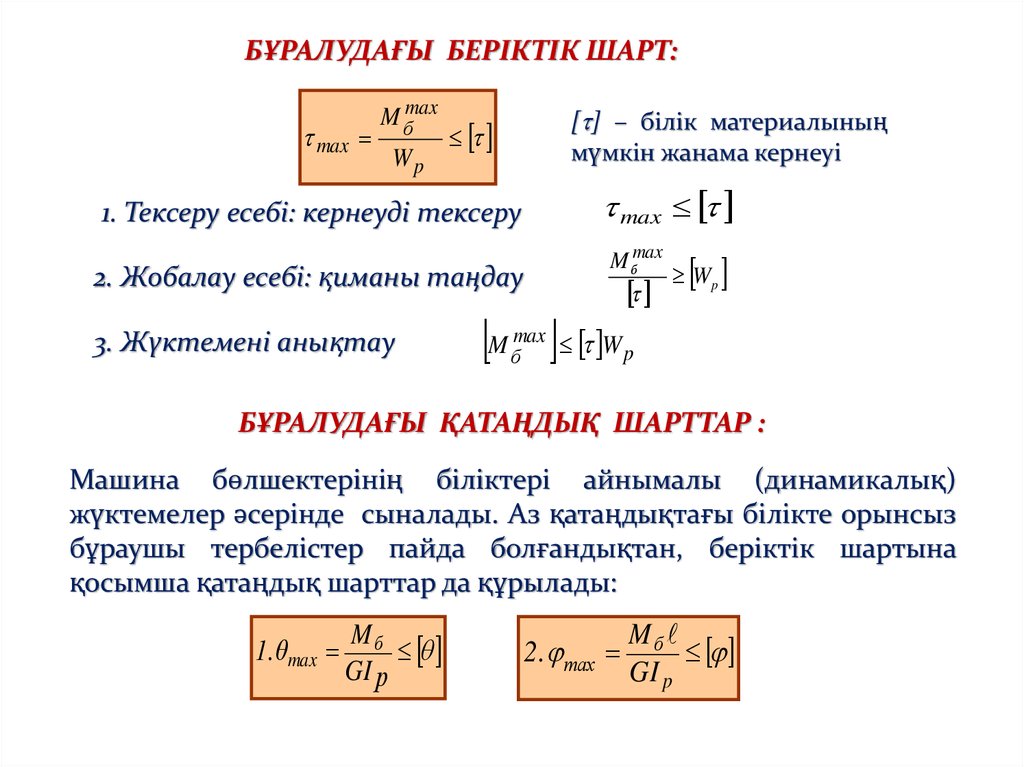
БҰРАЛУДАҒЫ БЕРІКТІК ШАРТ:max
M бmax
Wp
[ ] – білік материалының
мүмкін жанама кернеуі
1. Тексеру есебі: кернеуді тексеру
max
2. Жобалау есебі: қиманы таңдау
M бmax
Wp
3. Жүктемені анықтау
M W
max
б
p
БҰРАЛУДАҒЫ ҚАТАҢДЫҚ ШАРТТАР :
Машина бөлшектерінің біліктері айнымалы (динамикалық)
жүктемелер әсерінде сыналады. Аз қатаңдықтағы білікте орынсыз
бұраушы тербелістер пайда болғандықтан, беріктік шартына
қосымша қатаңдық шарттар да құрылады:
1.θmax
Mб
GI р
2. тах
M б
GI p
61.
ИІЛУИілуге жұмыс істейтін сырық арқалық
деп аталады
Сыртқы жүктеме әсерінен арқалықтың
көлденең қимасында тек қана Мz иілу
моменті пайда болатын деформация
түрі таза иілу деп аталады.
Сыртқы жүктеме әсерінен арқалықтың
көлденең қимасында Мz иілу моменті
және Qy көлденең күш пайда болатын
деформация түрі көлденең иілу деп
аталады.
62.
Qy таңбалар ережесіЕгер де қима жағынан қарағанда қалған бөлікті сыртқы
күш сағат тілімен бағыттас бұрса, онда осы қимадағы
көлденең күш оң таңбалы және керісінше
Мz таңбалар ережесі
егер қима жағынан қарағанда, қалған бөлік сыртқы
жүктеме әсерінен ойыс жағы төмен болатындай иілсе,
онда осы қимадағы иілу моменті оң таңбалы және
керісінше
63.
Иілудегі дифференциалдық тәуелділіктер – сыртқы жүктеме мен ішкікүш факторларын байланыстырады. Қарқындылығы q таралған
күшпен жүктелген арқалықтан элементар dх ұзындығын бөліп алып,
қалған бөлікке алып тастаған бөліктің әсерін ішкі күштер арқылы
өрнектейік:
y
q
MZ+dMZ
MZ Qy
O
x
Qy+dQy
dх
Элементар бөлік тепе-теңдік күйде болып, келесі статиканың тепетеңдік теңдеулерін қанағаттандырады:
Pyi 0;
Q y qdx (Q y dQ y ) 0;
M 0i 0; - M z qdx
dx
2
(Q y dQy )dx (M z dM z ) 0.
64.
Бірінші теңдеуден анықталады:dQ y
dx
q
Көлденең күштен ұзындық бойынша алынған бірінші туынды
таралған күштің қарқындылығына тең.
Екінші теңдеуден dх
ескеріп, анықталады:
екінші
dM z
dx
дәрежесін
өте
аз
шама
деп
Qy
Иілу моменттен ұзындық бойынша алынған бірінші туынды
көлденең күшке тең.
Негізгі тәуелділіктерді ескеріп:
2
d Mz
q
2
dх
Иілу моменттен ұзындық бойынша алынған екінші туынды таралған
күштің қарқындылығына тең.
65.
Qу ,Мz эпюраларын тұргызудағы ерекшеліктер.1. Егер арқалық сыртқы қадалған күшпен жүктелсе, онда Qy
эпюрінде осы күш түскен қимада күшке тең секіріс, ал Mz
эпюріне сынық сәйкес келеді.
2. Егер арқалық таралған күшпен жүктелмесе (q=0), онда Qy
эпюрі арқалық өсіне параллель түзумен, ал арқалықтың осы
аралығындағы Mz эпюрі көлбеу түзумен шектеледі.
3. Егер арқалық q таралған күшпен жүктелсе, онда Qy эпюрі
көлбеу түзумен, ал Mz
эпюрі параболамен шектеледі.
Параболаның дөңес жағы таралған күшке қарсы бағытталады.
4. Арқалықтың Qy=0 эпюрінде, Mz эпюрі - экстремум (масимум
не минимум) мәнге ие болады.
5. Егер арқалық сыртқы қадалған моментпен жүктелсе, онда Qy
эпюрі еш өзгеріссіз, ал Mz эпюрінде момент түскен қимада
моментке тең секіріс сәйкес келеді.
6. Арқалықтың Qy >0 эпюрі аралығында, Mz эпюрі өседі және
Qy <0 эпюрі аралығында, Mz эпюрі кемиді.
66.
Күш жазықтығы арқалықтың көлденең қимасының басты инерцияөстері арқылы өтсе, иілу көлденең жазық иілу деп аталады.
Таза иілу кернеулік күйінде
қолданылатын гипотазалар:
1.
Деформацияға дейінгі арқалық
өсіне перпендикуляр жазық қималары
деформациядан кейін де сол жазық
күйінде арқалық өсіне перпендикуляр
қалады (жазық қималар гипотезасы).
2. Деформация
кезінде
бойлық
талшықтар бір бірімен әсерлеспейді.
Таза иілудегі деформация ұшырамайтын қабат бейтарап қабат деп
аталады. Бейтарап қабаттың арқалықтың көлденең қимасымен
қиылысу сызығы бейтарап өс болып табылады.
67.
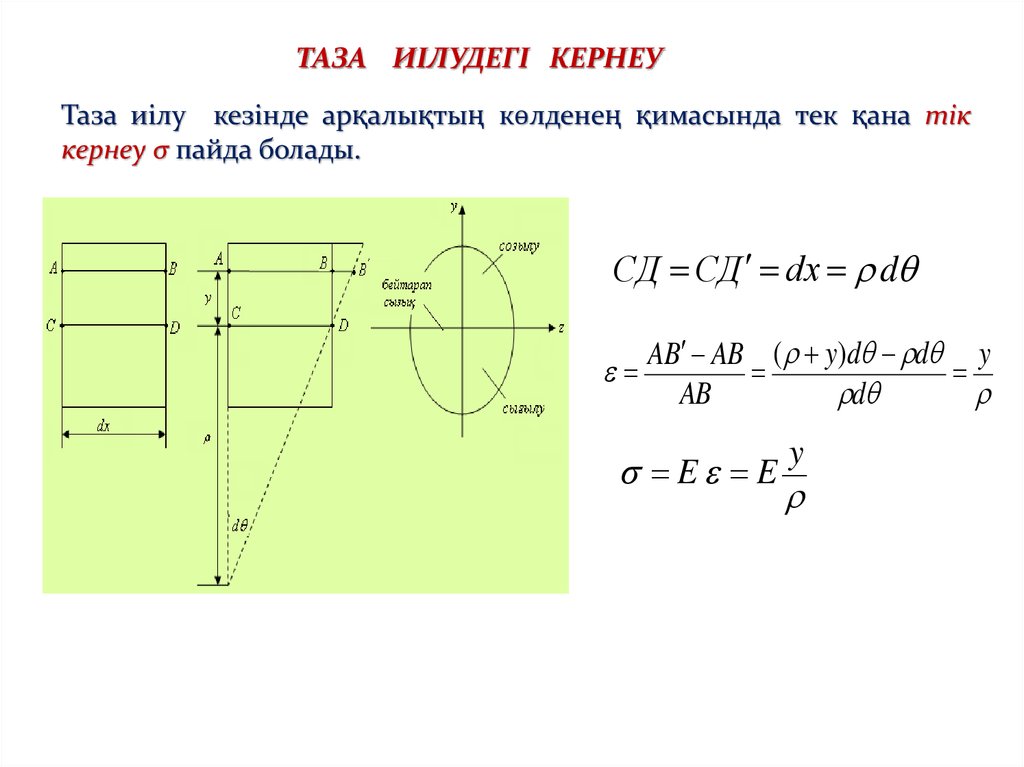
ТАЗА ИІЛУДЕГІ КЕРНЕУТаза иілу кезінде арқалықтың көлденең қимасында тек қана тік
кернеу σ пайда болады.
СД СД dх d
AB AB ( y)d d y
AB
d
E E
y
68.
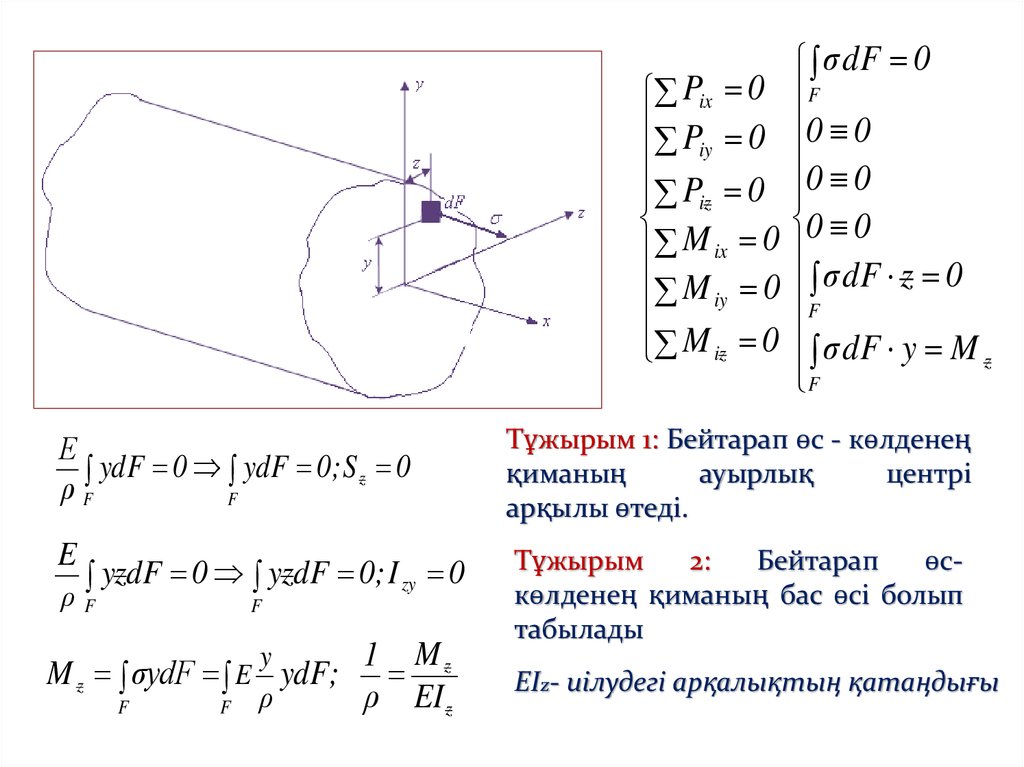
Pix 0Piy 0
P 0
iz
M ix 0
M 0
iy
M iz 0
σ dF 0
F
0 0
0 0
0 0
σ dF z 0
F
σ dF y M
z
F
Е
ydF 0 ydF 0; S z 0
ρF
F
Тұжырым 1: Бейтарап өс - көлденең
қиманың
ауырлық
центрі
арқылы өтеді.
E
Тұжырым
2:
Бейтарап
өскөлденең қиманың бас өсі болып
табылады
yzdF 0 yzdF 0; I zy 0
ρF
F
y
1 Mz
M z σydF E ydF;
ρ EI z
F
F ρ
ЕIz- иілудегі арқалықтың қатаңдығы
69.
σMz
у
Iz
Бейтарап өске симметриялы көлденең қима кернеулерінің абсолют
шамасы бойынша ең үлкен және ең кіші мәндері келесі формуламен
анықталады:
σ тах
Mz
утах
Iz
Көлденең қиманың өлшемдері мен пішініне байланысты анықталатын
геометриялық шама өстік қарсыласу моменті деп аталады:
Wz
Iz
3
3
[
см
,
м
]
ymax
Тік кернеудің максималь мәні өстік қарсыласу моментін ескерсек,
келесі формуламен анықталады:
Mz
σ тах
Wz
70.
ҚИМАНЫҢ ҚАРСЫЛАСУ МОМЕНТТЕРІТөртбұрышты қима:
y
h
Wz
z
Iz
ymax
b
Дөңгелек қима:
y
D
bh 3
b3h
Iy
bh 2
b2h
12
12
, Wy
h
b
6
z max
6
2
2
Wz W у
z
R
Сақина кимасы:
y
Wz W у
D d
Iz
ymax
πR 4
πR 3 πD 3
4
0,1D 3
R
4
32
z
k
d
D
Iz
ymax
π(R 4 r 4 )
π(R 3 r 3 ) π(D 3 - d 3 )
4
0,1D 3 (1 k 4 ),
R
4
32
71.
БЕРІКТІК ШАРТЫМ max
σ
max
z
Wz
σ
арқалық материалының
мүмкін кернеуі
ЕСЕПТЕУ ТҮРЛЕРІ
σ max σ
1. Тексеру есебі: беріктікті тексеру.
Кернеудің есептеу мәні мүмкін кернеуден 5 % артық мәні қабылданады.
2. Жобалау есебі: қиманы таңдау. Конструкция элементерінің көлденең
қимасының геометриялық өлшемін анықтау .
M max
Wz
3. Жүктелуді есептеу: мүмкін моментті анықтау.
ПОТЕНЦИЯЛЫҚ ЭНЕРГИЯ
2
U
Mzl
2EI z
z
σ
[М z ] Wz [ ]
72.
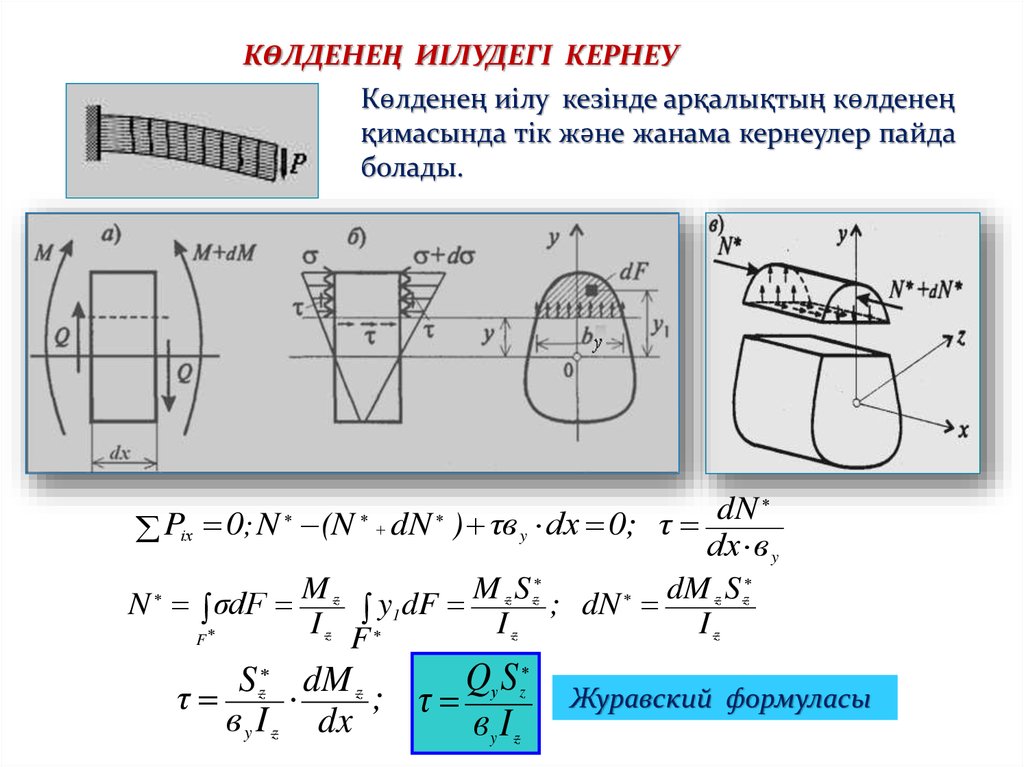
КӨЛДЕНЕҢ ИІЛУДЕГІ КЕРНЕУКөлденең иілу кезінде арқалықтың көлденең
қимасында тік және жанама кернеулер пайда
болады.
dN
Piх 0; N (N dN ) τв y dх 0; τ
dх в y
M
M
dM
z
z Sz
z Sz
N σdF
y1dF
; dN
Iz F
Iz
Iz
F
Q
S
S
dM
z
τ z
; τ у z
в y I z dx
вy I z
Журавский формуласы
73.
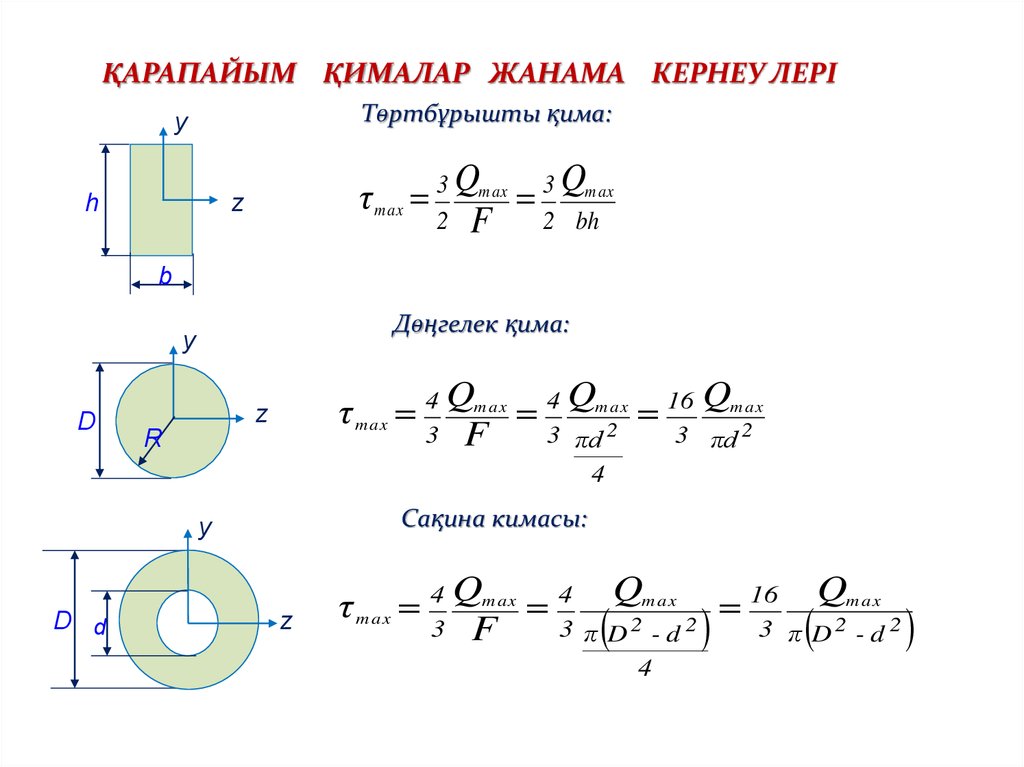
ҚАРАПАЙЫМ ҚИМАЛАР ЖАНАМА КЕРНЕУ ЛЕРІТөртбұрышты қима:
y
h
τ m ax 3 Qm ax 3 Qm ax
2 F
2 bh
z
b
Дөңгелек қима:
y
D
τ m ax 4 Qm ax 4 Qm2ax 16 Qm2ax
3 F
3 πd
3 πd
z
R
4
Сақина кимасы:
y
D d
z
τ m ax 4 Qm ax 4 Q2m ax 2 16 Q2m ax 2
3 F
3 π D - d
3 π D - d
4
74.
тік және жанама кернеулер эпюріy
z
ИІЛУДЕГІ ТОЛЫҚ ЕСЕПТЕУ:
Иілудегі толық есептеу келесі қауіпті қималар үшін анықталады:
1) Модулі бойынша Mz иілу моментінің ең үлкен мәніне сәйкес қима –
осы қима үшін арқалықтың қимасы таңдалады;
2) Модулі бойынша Qy көлденең күштің ең үлкен мәніне сәйкес қима ;
3) Модулдері бойынша Mz иілу моментінің және Qy көлденең күштің ең
үлкен мәндеріне сәйкес қима .
1. max [ ]
2. τ
m ax
[τ ]
75.
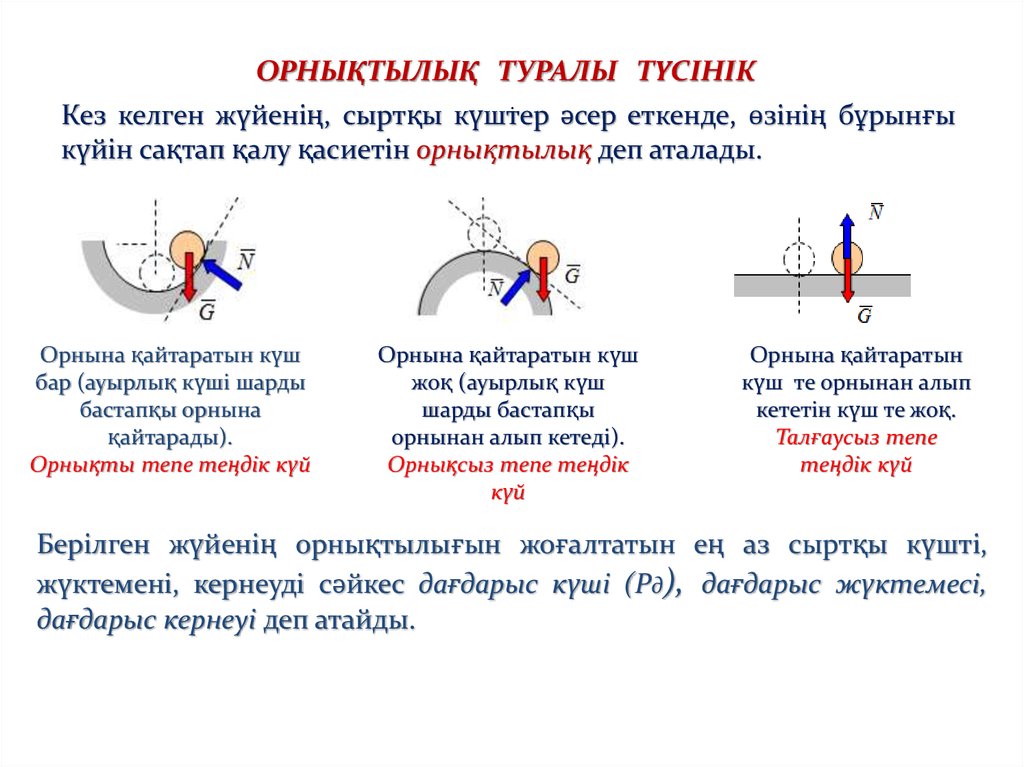
ОРНЫҚТЫЛЫҚ ТУРАЛЫ ТҮСІНІК.
Кез келген жүйенің, сыртқы күштер әсер еткенде, өзінің бұрынғы
күйін сақтап қалу қасиетін орнықтылық деп аталады.
Орнына қайтаратын күш
бар (ауырлық күші шарды
бастапқы орнына
қайтарады).
Орнықты тепе теңдік күй
Орнына қайтаратын күш
жоқ (ауырлық күш
шарды бастапқы
орнынан алып кетеді).
Орнықсыз тепе теңдік
күй
Орнына қайтаратын
күш те орнынан алып
кететін күш те жоқ.
Талғаусыз тепе
теңдік күй
Берілген жүйенің орнықтылығын жоғалтатын ең аз сыртқы күшті,
жүктемені, кернеуді сәйкес дағдарыс күші (Рд), дағдарыс жүктемесі,
дағдарыс кернеуі деп атайды.
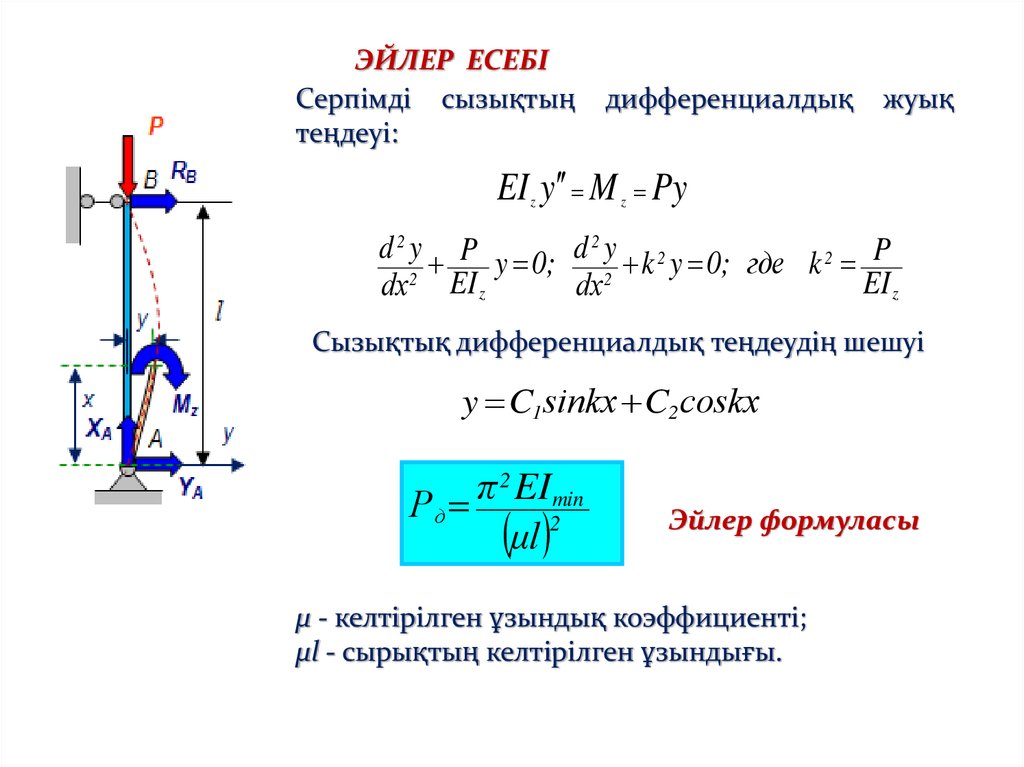
76.
ЭЙЛЕР ЕСЕБІСерпімді сызықтың
теңдеуі:
дифференциалдық
жуық
EI y M Py
z
z
d 2 y P y 0; d 2 y k 2 y 0; где k 2 P
EI z
dх 2 EI z
dх 2
Сызықтық дифференциалдық теңдеудің шешуі
y C1sinkх C2coskх
2
π
Р д EI2min
μl
Эйлер формуласы
μ - келтірілген ұзындық коэффициенті;
μl - сырықтың келтірілген ұзындығы.
77.
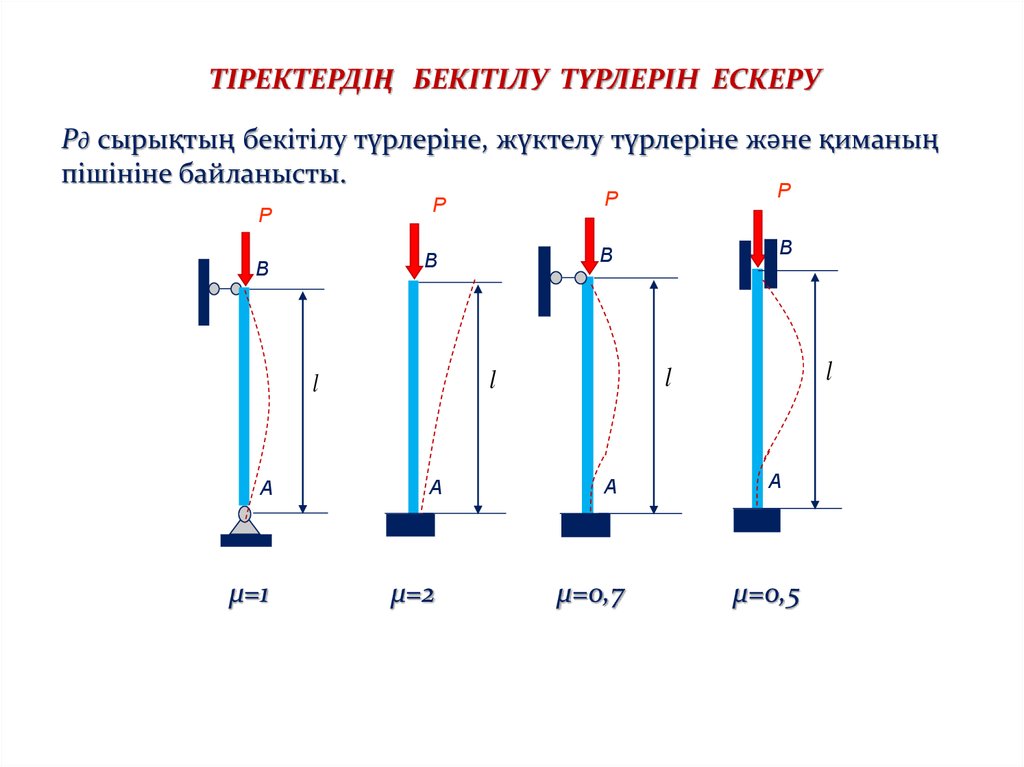
ТІРЕКТЕРДІҢ БЕКІТІЛУ ТҮРЛЕРІН ЕСКЕРУРд сырықтың бекітілу түрлеріне, жүктелу түрлеріне және қиманың
пішініне байланысты.
Р
Р
B
B
μ=1
Р
B
B
A
μ=2
l
l
l
l
A
Р
A
μ=0,7
A
μ=0,5
78.
ЭЙЛЕР ФОРМУЛАСЫНЫҢ ҚОЛДАНУ ШЕГІСырықтың серпімлі сызығының дифференциалдық теңдеуін интегралдау
арқылы Эйлер формуласы анықталады. Бұл теңдеу кернеу мен деформация
арасындағы сызықтық тәуелділік шегінде ғана орындалатындықтан, Эйлер
формуласы бойынша дағдарыс кернеуі σпц пропорциональдықтың шегінен
аспайтындай анықталады, яғни
2
Р
π
д
σ д EI2 min σ пц
F μl F
i2min=Imin/F теңдіктерін пайдаланып, мұндағы imin сырықтың көлденең қимасының ең кіші иенрция
радиусы, сонда бұл шарт жазылады:
λ - сырықтың майысқыштығы деп аталады,
μl
сырық өлшемдеріне,
тірек
түрлеріне λ
imin
байланысты өлшемсіз шама :
Эйлер формуласы сырықтың майысқыштығы
2
π
σ д 2E σ пц
λ
2Е
пц
жұмсақ көміртекті болат материалы үшін σпц=210МПа және E=2.1·105МПа
Яғни, Эйлер формуласының қолдану шегі :
λ λ 100
79.
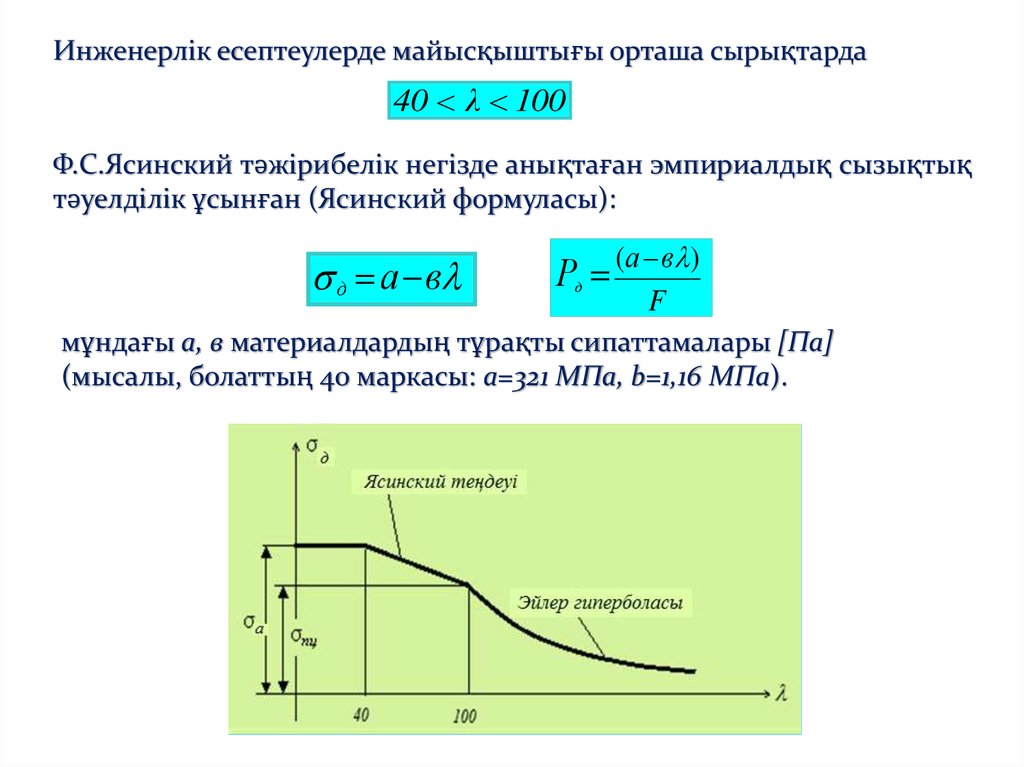
Инженерлік есептеулерде майысқыштығы орташа сырықтарда40 λ 100
Ф.С.Ясинский тәжірибелік негізде анықтаған эмпириалдық сызықтық
тәуелділік ұсынған (Ясинский формуласы):
д а в
Р (а в )
д
F
мұндағы а, в материалдардың тұрақты сипаттамалары [Па]
(мысалы, болаттың 40 маркасы: a=321 МПа, b=1,16 МПа).
80.
ОРНЫҚТЫЛЫҚ ШАРТЫСырықтың орнықылығын қамтамасыз ететін шарт:
σ
σд
nорын
σ орын .
мұндағы nорын – кор коэффициенті,
[ орын] – орнықтылықтағы мүмкін кернеу.
σ σ
орын
φ мүмкін кернеуді төмендету коэффициенті. Бұл коэффициенттің
мәндері Құрылыстық ережелер мен нормалар (СНИП) арқылы
тағайындалған, таблица арқылы майысқыштықтың функция
түрінде әртүрлі маркалы болат және басқа материалдарға
(шойын,ағаш) берілген.


























































 Механика
Механика








