Похожие презентации:
Электрическое поле в вакууме
1.
Рекомендуемаялитература
Основная
1. Савельев «Курс Общей Физики»,
2. А.А. Деталаф, , В.М. В.М. Яворский «Курс Общей
Физики» М., Высшая школа, 2000.
3. Волькинштейн С.В. «Сборник задач по общей физике»
Дополнительная
1. Фейман Р. Феймановские лекции по физике. М. Мир. 1967, тт. 5,6,7
2. Иродов И.Е. Основные законы электромагнетизма. М. Наука, 2001
3. Берклеевский Курс физики. – М., Наука, 1986.
2.
Электрическое поле в вакуумеЭлектрический заряд
1. Положительный и отрицательный
2. Закон сохранения заряда
3. Инвариантная величина
4. Квантование заряда
е = 1,6 10 19 Кл (Кулон).
qi const .
e e
e e
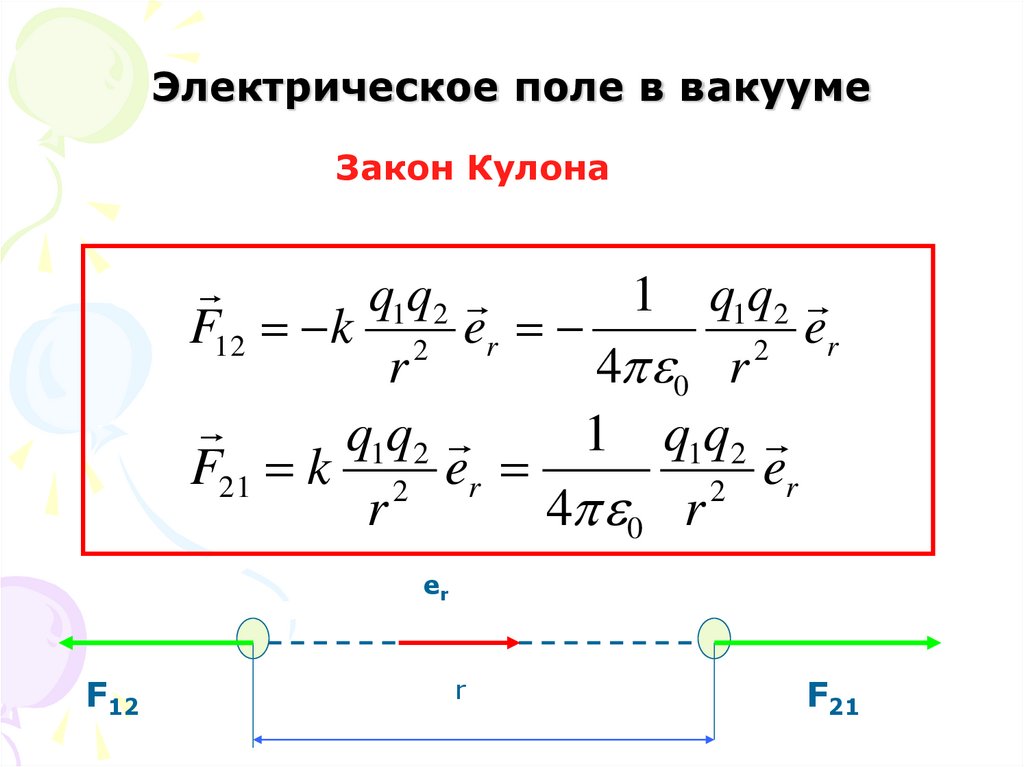
3. Электрическое поле в вакууме
Закон Кулонаq1q2
1 q1q2
F12 k 2 er
er
2
r
4 0 r
q1q2
1 q1q2
F21 k 2 er
er
2
r
4 0 r
er
F12
r
F21
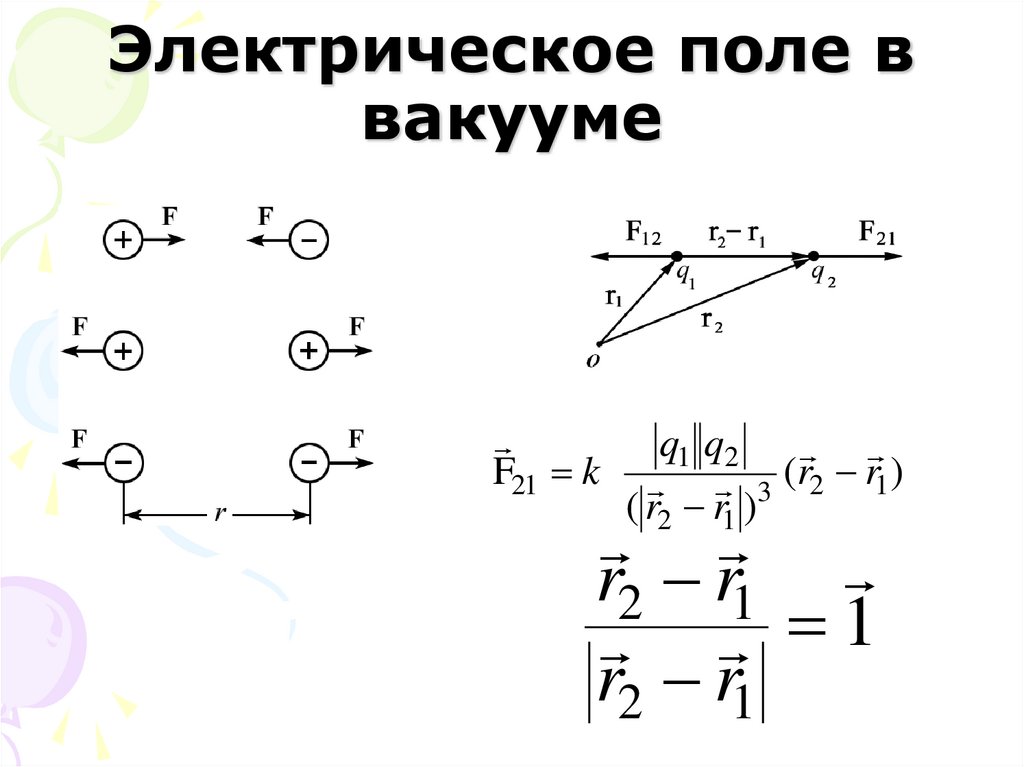
4. Электрическое поле в вакууме
F21 kq1 q2
3 (r2 r1 )
( r2 r1 )
r2 r1
1
r2 r1
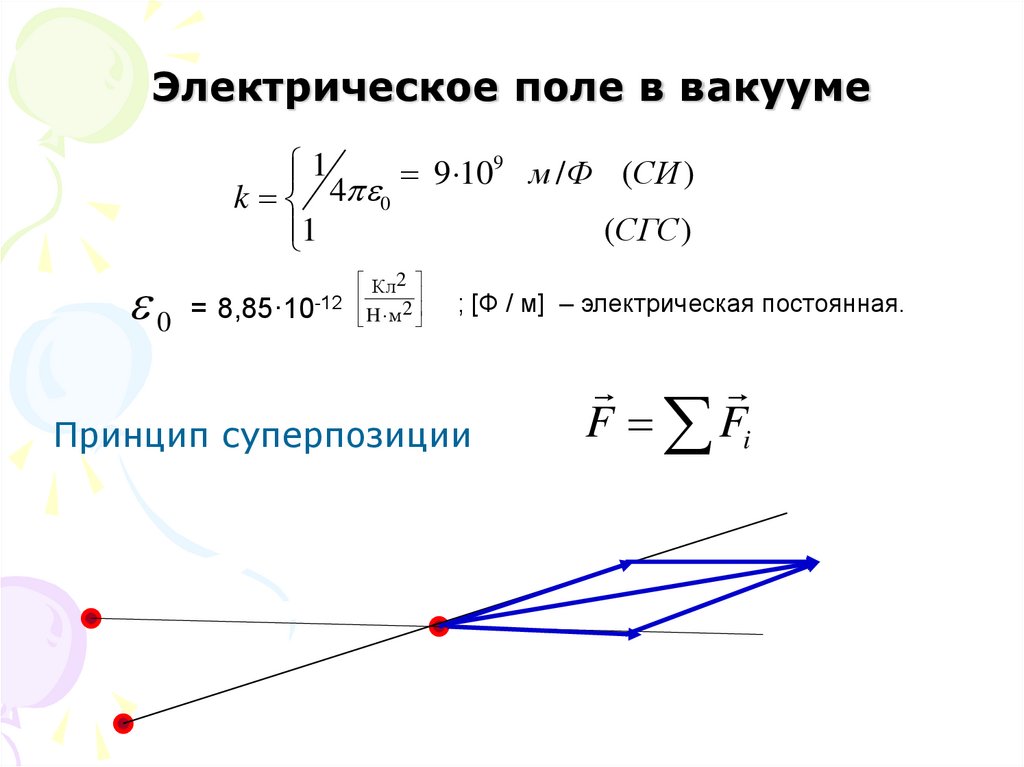
5. Электрическое поле в вакууме
91
9
10
м /Ф (СИ )
4
k
0
(СГС )
1
0 = 8,85·10
-12
Кл2
H м2
; [Ф / м] – электрическая постоянная.
Принцип суперпозиции
F Fi
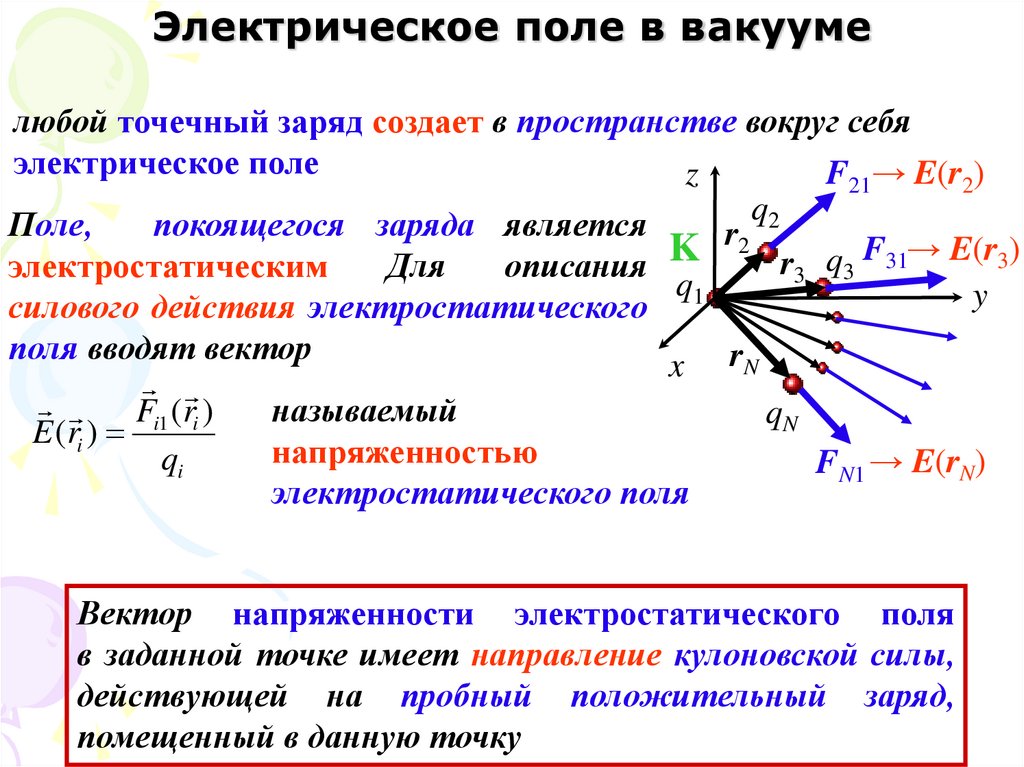
6. Электрическое поле в вакууме
любой точечный заряд создает в пространстве вокруг себяэлектрическое поле
F21→ E(r2)
z
q2
Поле,
покоящегося заряда является
r2
K
r3 q3 F31→ E(r3)
электростатическим
Для
описания
q1
y
силового действия электростатического
поля вводят вектор
x
F (r )
называемый
E (ri ) i1 i
напряженностью
qi
электростатического поля
rN
qN
FN1 → E(rN)
Вектор напряженности электростатического поля
в заданной точке имеет направление кулоновской силы,
действующей на пробный положительный заряд,
помещенный в данную точку
7. Электрическое поле в вакууме
Электрическое поле – особая формасуществования материи, посредством которой
взаимодействуют электрические заряды.
Напряженность электрического поля в
данной точке – физическая величина, определяемая
силой, действующей на пробный положительный
точечный единичный заряд q, помещенный в эту
точку поля.
F qE
E
q
2 er
4 0 r
1
8. Электрическое поле в вакууме
Заряд q измеряется вкулонах (Кл)
Напряженность поля E в
вольтах на метр (В/м)
E Ex i E y j Ez k
E
2
2
2
Ex E y Ez
9. Электрическое поле в вакууме
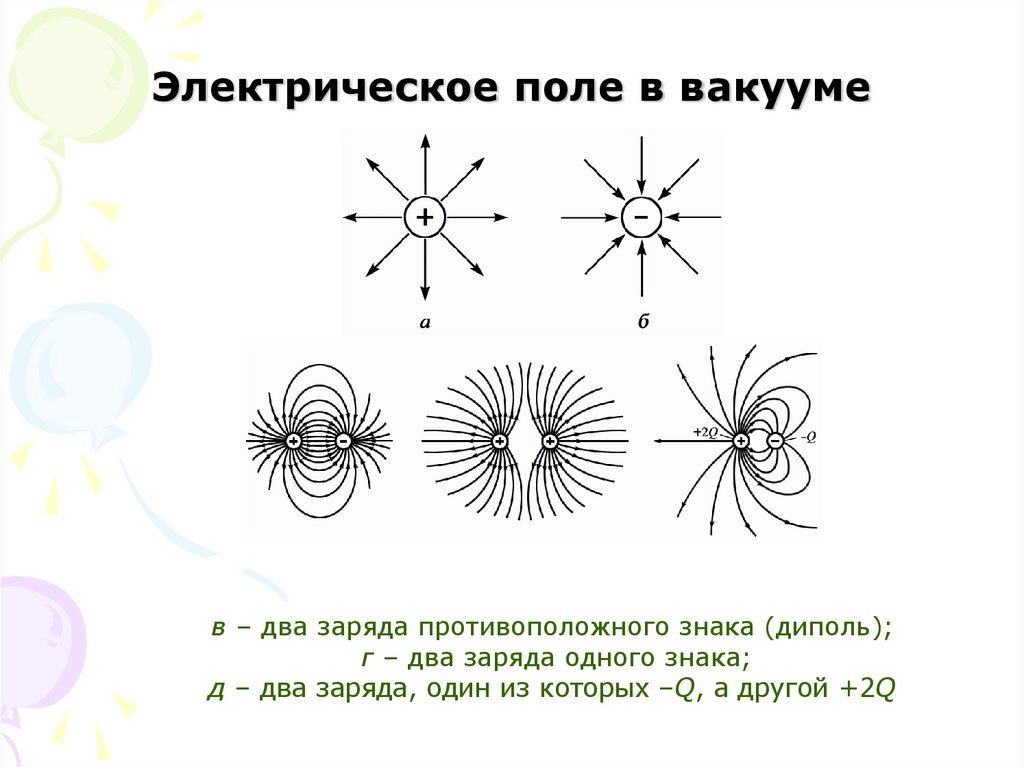
в – два заряда противоположного знака (диполь);г – два заряда одного знака;
д – два заряда, один из которых –Q, а другой +2Q
10. Электрическое поле в вакууме
Принцип суперпозицииn
F F1 F2 ... Fn Fi
F q0 E
i 1
Fi q0 Ei
E Ei
n
q0 E q0 Ei
E
i 1
qi
e
2 ri
4 0
ri
1
11. Электрическое поле в вакууме
Распределение зарядовdq
dq
,
dV
dq
,
dS
dq
dl
1
er
1
r
E
dV
dV
2
3
4 0
r
4 0 r
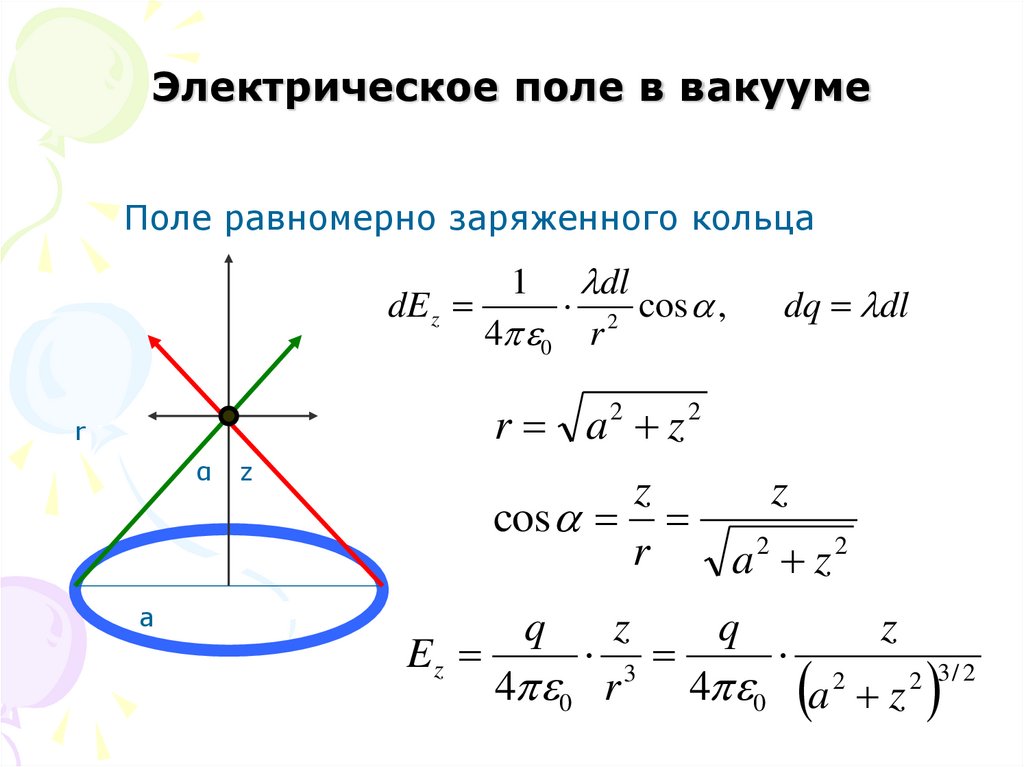
12. Электрическое поле в вакууме
Поле равномерно заряженного кольцаdE z
1
4 0
dl
r
2
α
a
z
dq dl
r a z
z
z
cos
r
a2 z 2
2
r
cos ,
q
2
z
q
z
Ez
3
4 0 r
4 0 a 2 z 2 3 / 2
13. Электрическое поле в вакууме Потенциал
W Fdsb
a
b
b
Fds Fds
a'
a
a'
a’
q 1 1
Fds
4 0 ra rb
a'
b
a
14. Электрическое поле в вакууме Потенциал
bW Eds b a
a
P Eds Eds
P
P
P0
r
1
1
i 4 0 r1i
q
dV2
1
4 0 r12
q
1
4 0 r
15. Электрическое поле в вакууме Связь напряженности и потенциала
W x x, y, z x, y, zx
x
W Eds E x x
Ex
x
E grad
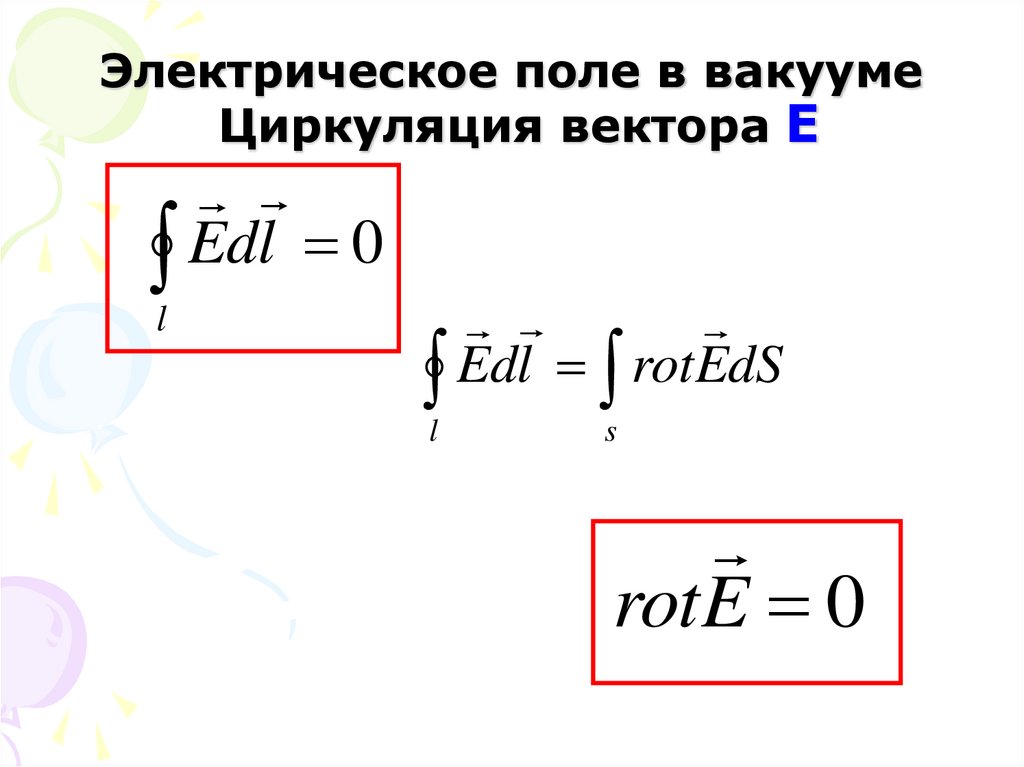
16. Электрическое поле в вакууме Циркуляция вектора E
A12 Edl2
1
a
2
A12 Edl
A21 Edl
(12 ) b
(12 ) a
b
1
A12 A21
Edl Edl
( 21)b
(12 ) a
17. Электрическое поле в вакууме Циркуляция вектора E
Ed
l
0
l
Edl rotEdS
l
s
rotE 0
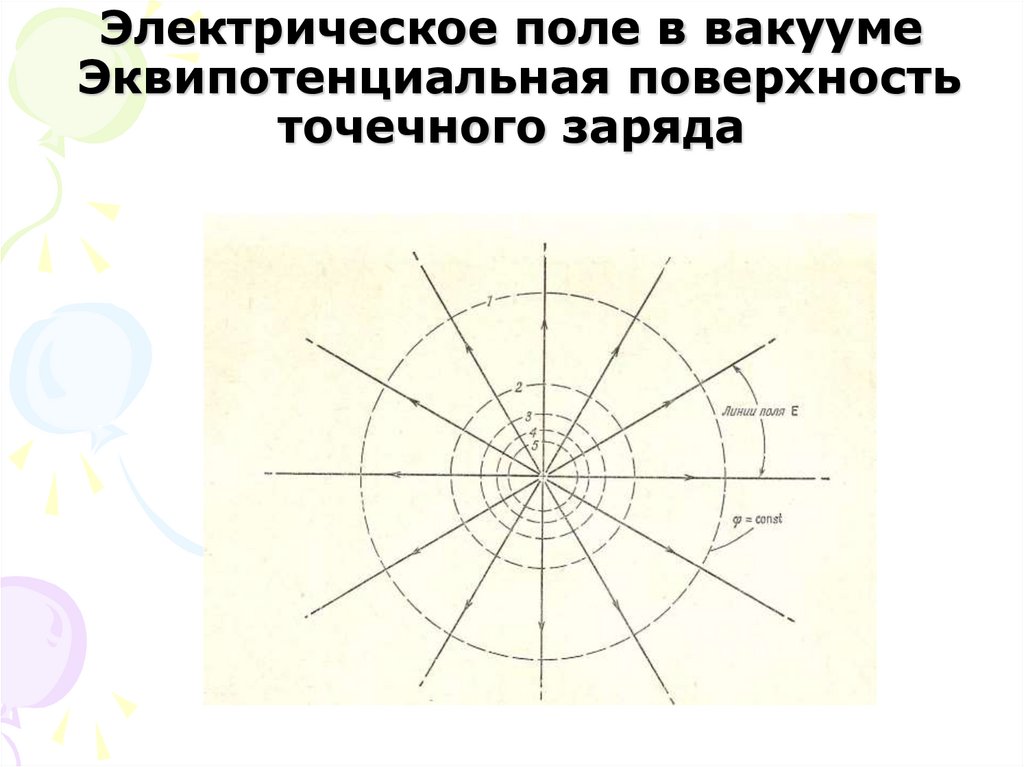
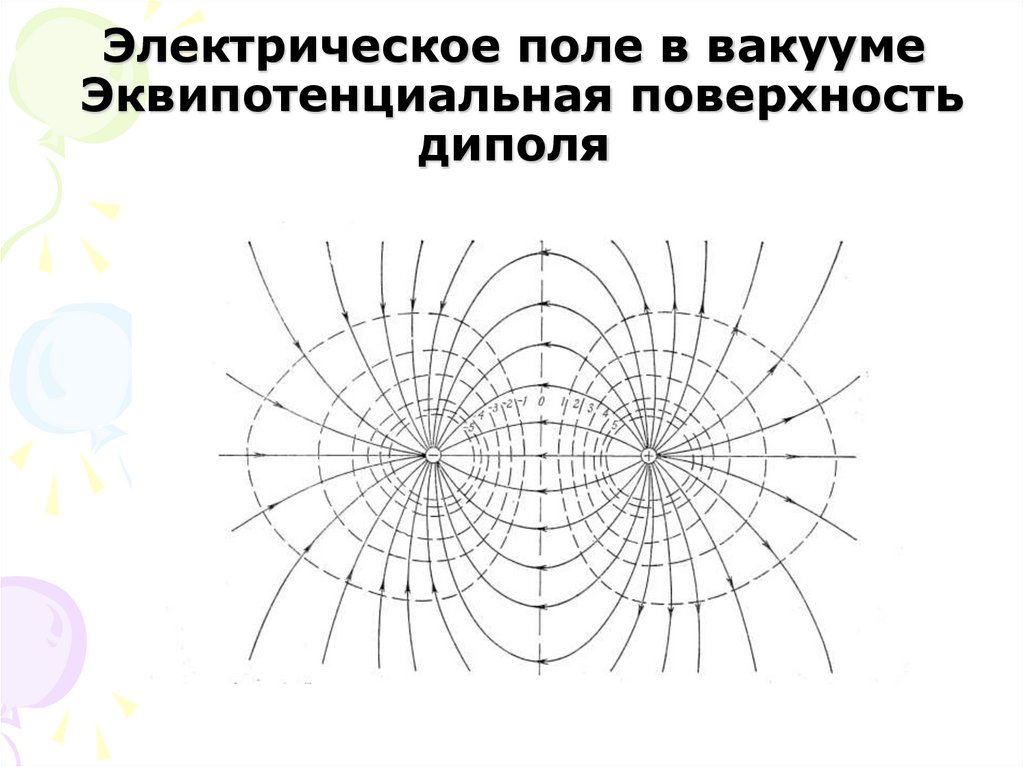
18. Электрическое поле в вакууме Эквипотенциальная поверхность
r constE l 0
Вектор E перпендикулярен эквипотенциальной
поверхности
19. Электрическое поле в вакууме Эквипотенциальная поверхность точечного заряда
20. Электрическое поле в вакууме Эквипотенциальная поверхность диполя
21. Электрическое поле в вакууме Теорема Гаусса
Поток вектора Е сквозь замкнутую поверхностьравен алгебраической сумме зарядов внутри
данной этой поверхности, деленной на ε0
S Ads
S
dS
A
dS
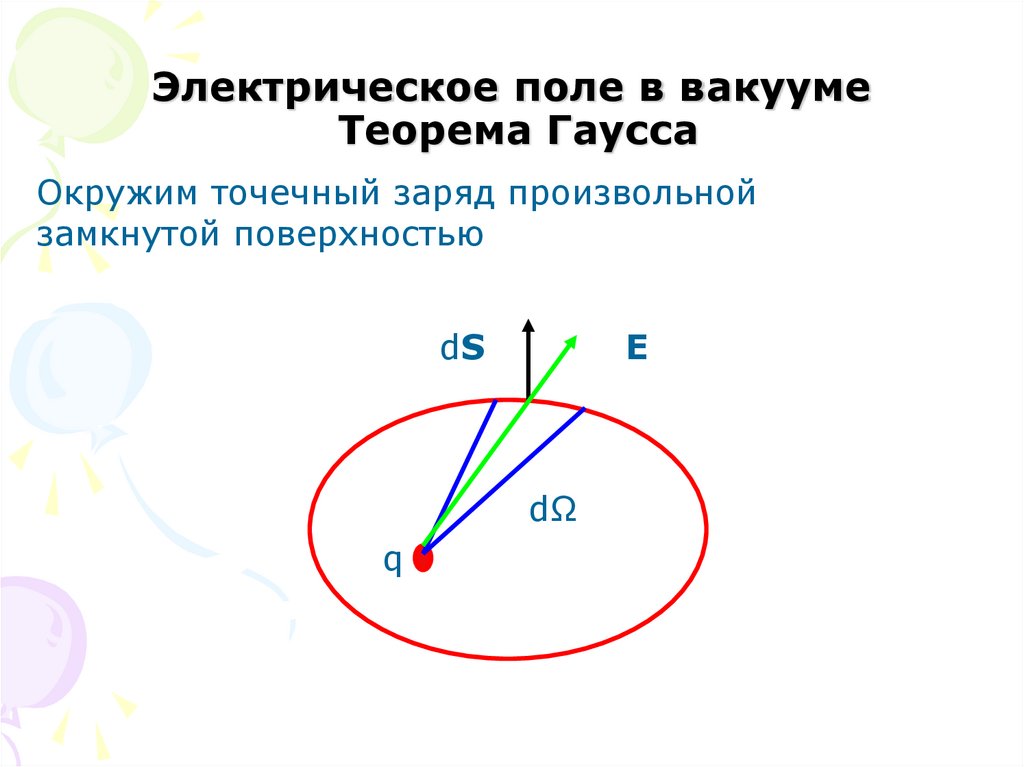
22. Электрическое поле в вакууме Теорема Гаусса
Окружим точечный заряд произвольнойзамкнутой поверхностью
dS
E
dΩ
q
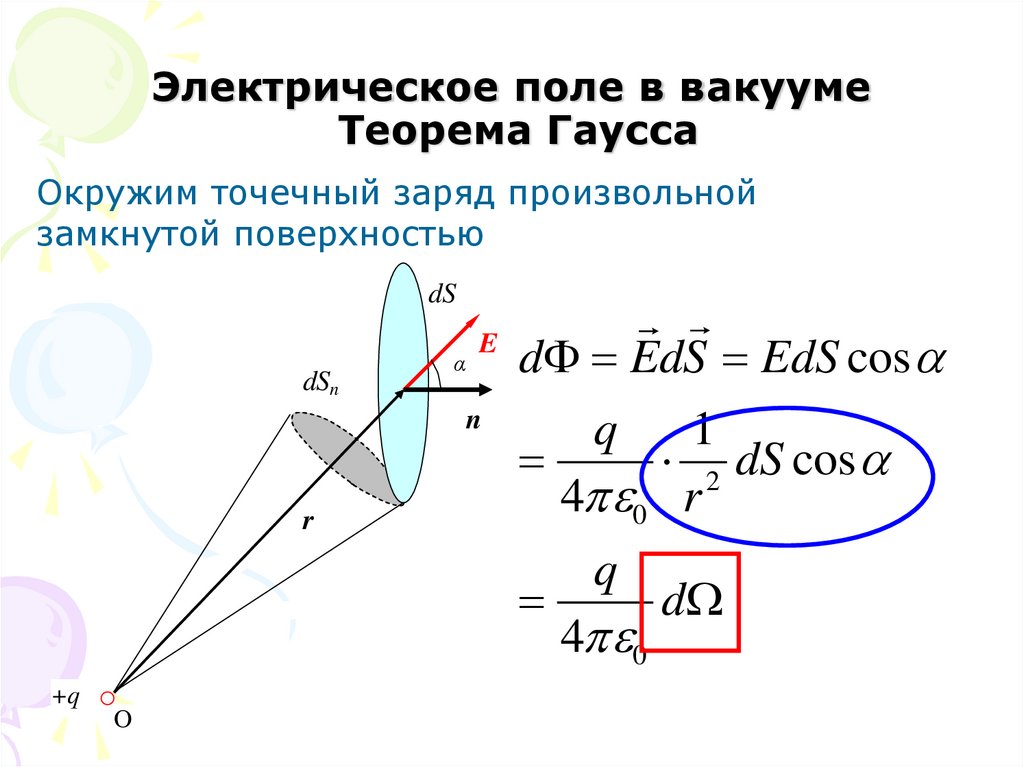
23. Электрическое поле в вакууме Теорема Гаусса
Окружим точечный заряд произвольнойзамкнутой поверхностью
dS
dSn
r
E
α
d EdS EdS cos
n
q
1
2 dS cos
4 0 r
+q
O
q
4 0
d
24. Электрическое поле в вакууме Теорема Гаусса
Интегрирование по телесному углу дастd 4
q
EdS
S
0
EdS E1 E2 E3 ... dS 1 2 3 ...
s
s
q1 q2 q3 ... / 0 qi / 0 dV / 0
Q
EdS
S
0
25. Электрическое поле в вакууме Теорема Гаусса
Теорема Гаусса в дифференциальной форме1
EdS divEdV dV
S
V
0 V
E divE / 0
Ex E y Ez
divE
x
y
z
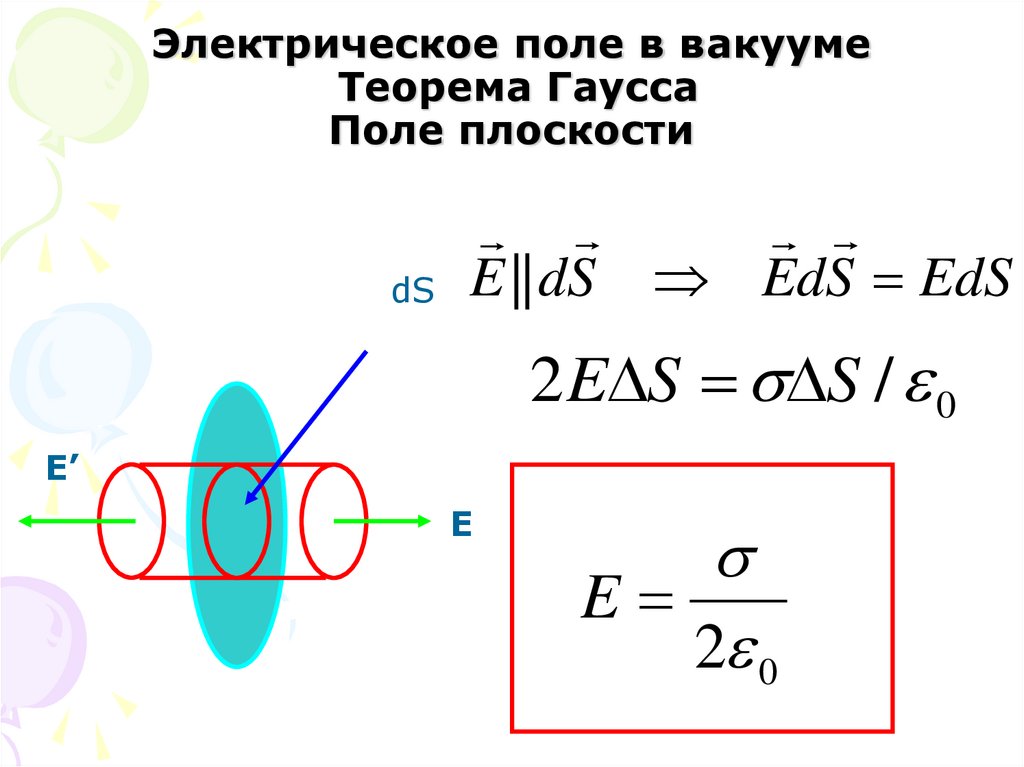
26. Электрическое поле в вакууме Теорема Гаусса Поле плоскости
EdS EdSdS E || dS
2 E S S / 0
E’
E
E
2 0
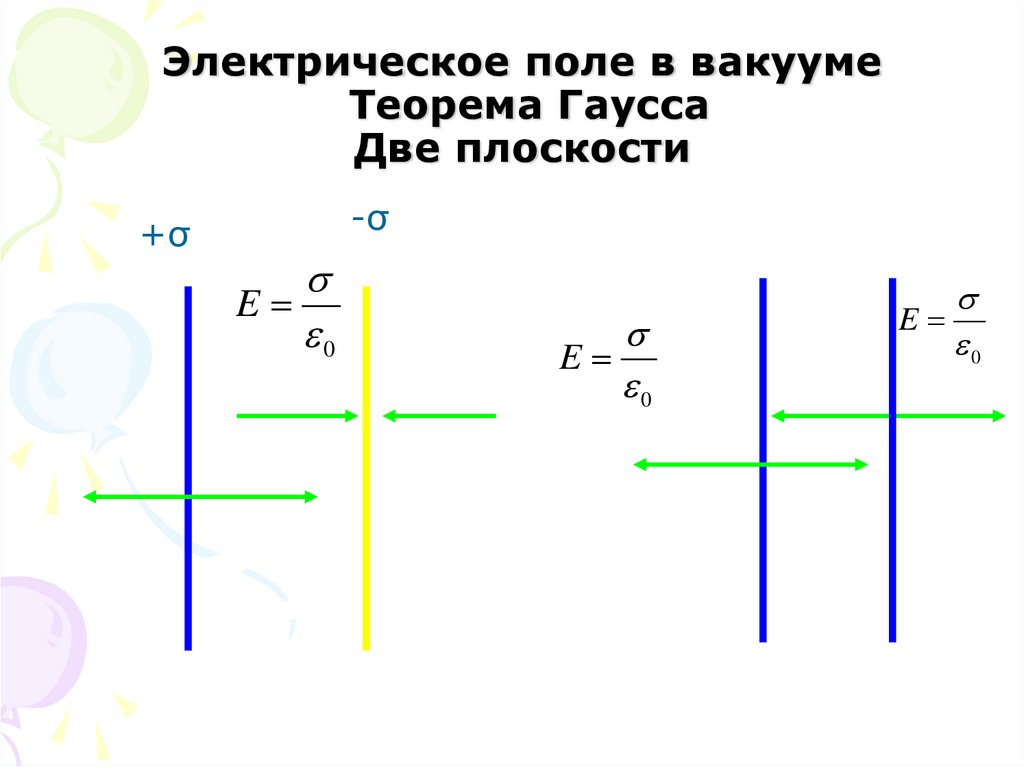
27. Электрическое поле в вакууме Теорема Гаусса Две плоскости
+σ-σ
E
0
E
0
E
0
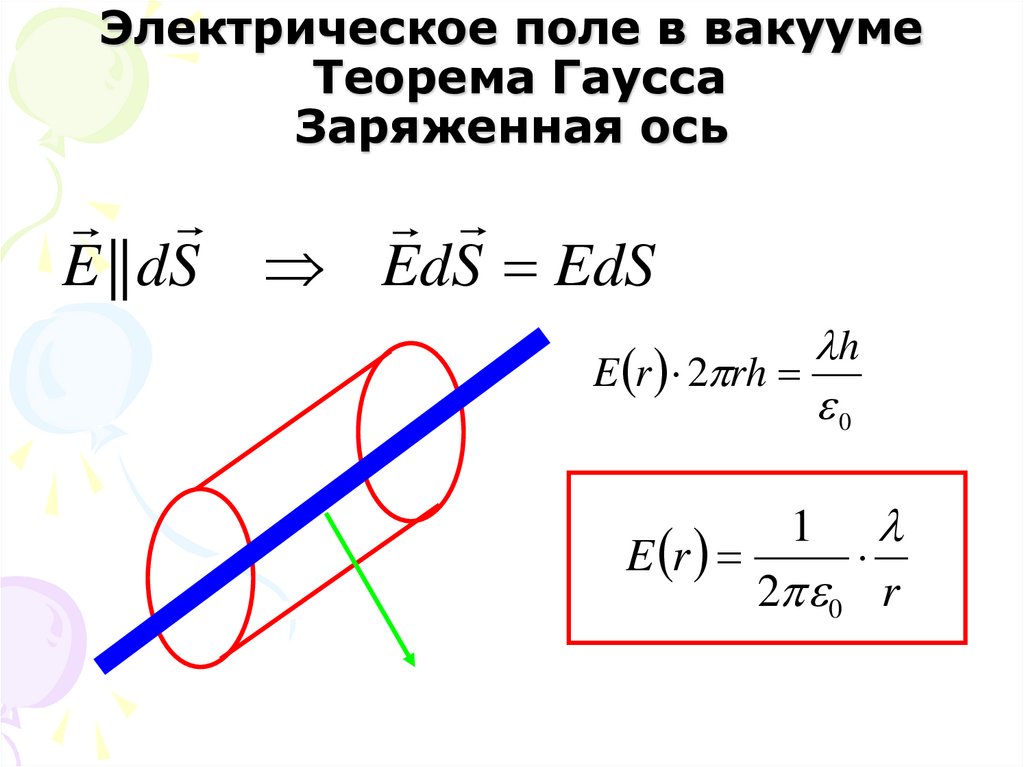
28. Электрическое поле в вакууме Теорема Гаусса Заряженная ось
E || dS EdS EdSh
E r 2 rh
0
E r
1
2 0 r
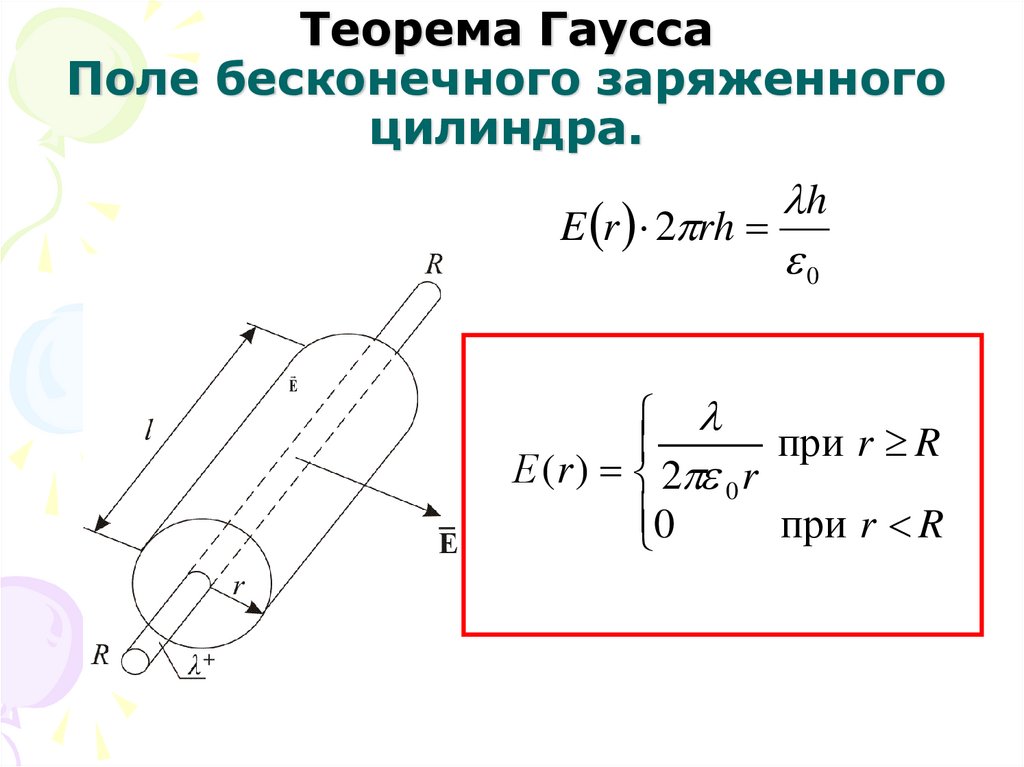
29. Теорема Гаусса Поле бесконечного заряженного цилиндра.
hE r 2 rh
0
E
при r R
Е ( r ) 2 0 r
0
при r R
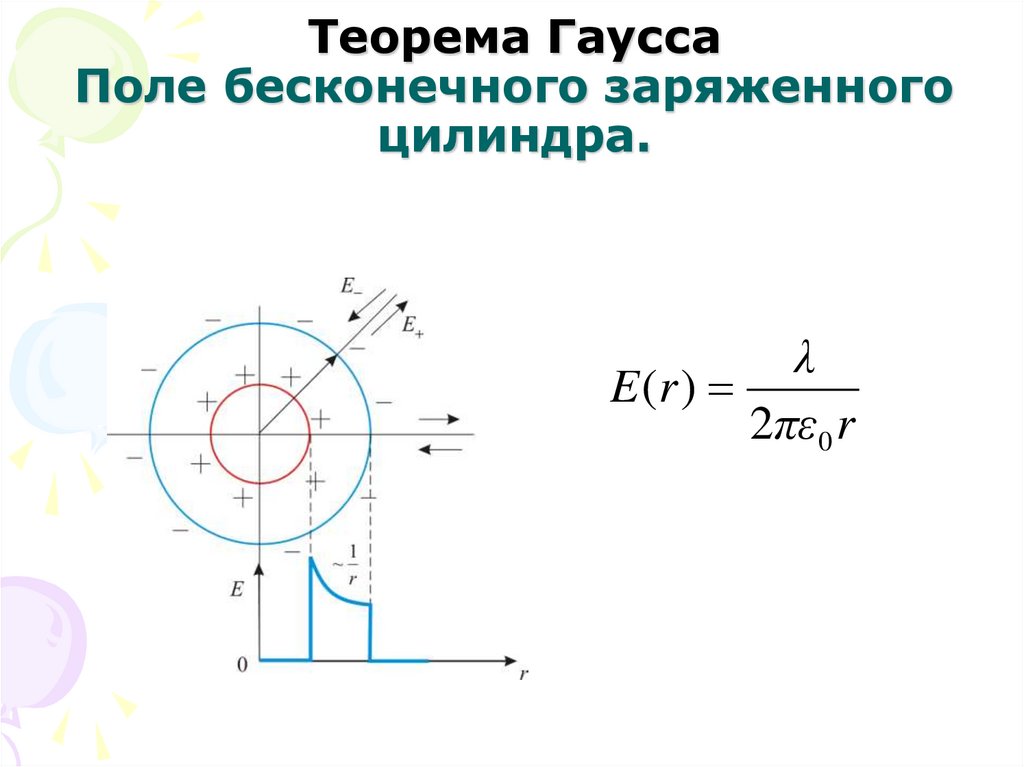
30. Теорема Гаусса Поле бесконечного заряженного цилиндра.
λE (r )
2πε 0 r
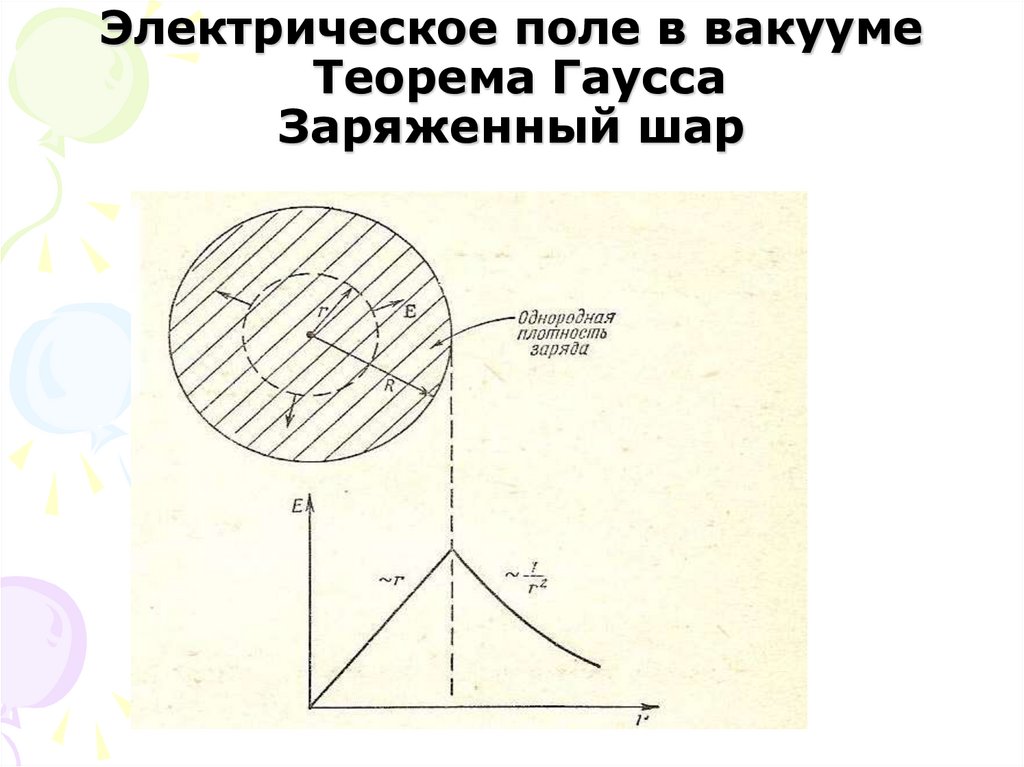
31. Электрическое поле в вакууме Теорема Гаусса Заряженный шар
E || dS EdS EdSE r const
4 3 V Q
E r 4 r
r
0
3
0
0
2
1
E r
1
3 0
r
r R
32. Электрическое поле в вакууме Теорема Гаусса Заряженный шар
E || dS EdS EdSE r const
4 3 1
E r 4 r R Q
0 3
0
2
1
Q
E r
4 0 r 2
1
r R
33. Электрическое поле в вакууме Теорема Гаусса Заряженный шар
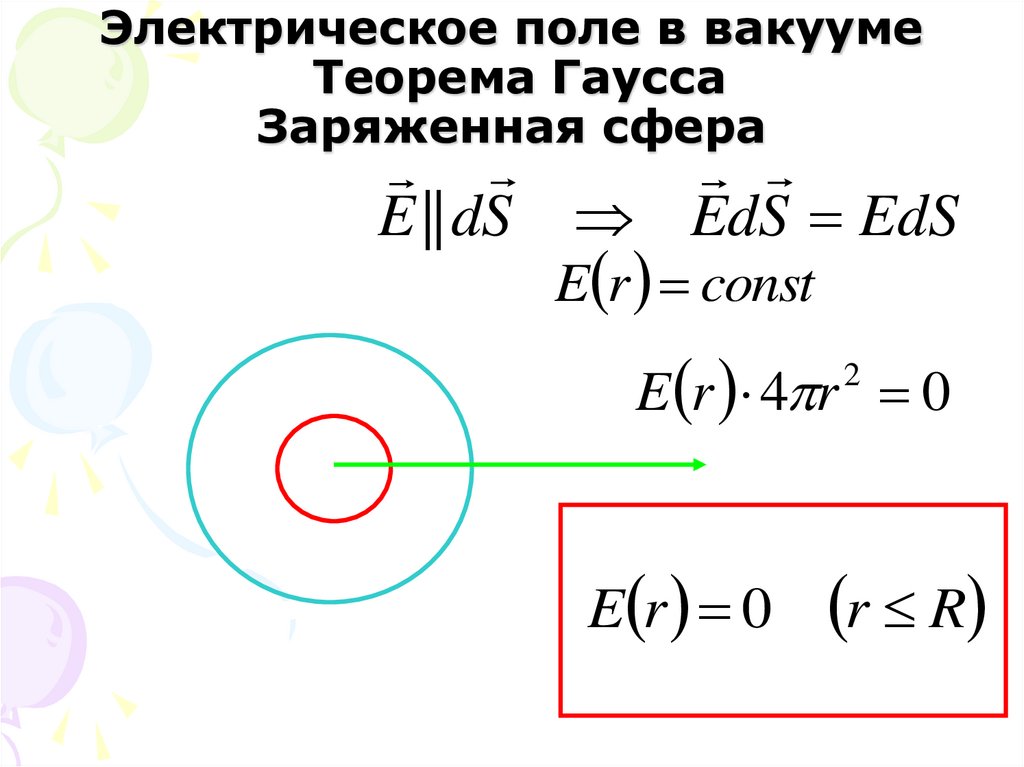
34. Электрическое поле в вакууме Теорема Гаусса Заряженная сфера
E || dS EdS EdSE r const
E r 4 r 0
2
E r 0
r R
35. Электрическое поле в вакууме Теорема Гаусса Заряженная сфера
E || dS EdS EdSE r const
E r 4 r
2
1
0
2 R
2
Q
E r
4 0 r 2
1
1
0
r R
Q
36. Теорема Ирншоу
Системанеподвижных
электрических
зарядов не может находиться в устойчивом
равновесии.
E , n E , dS 180 0
ФЕ EdS EdS cos( E , dS )
S
S бок
EdS cos1800 0
S
ФЕ 0
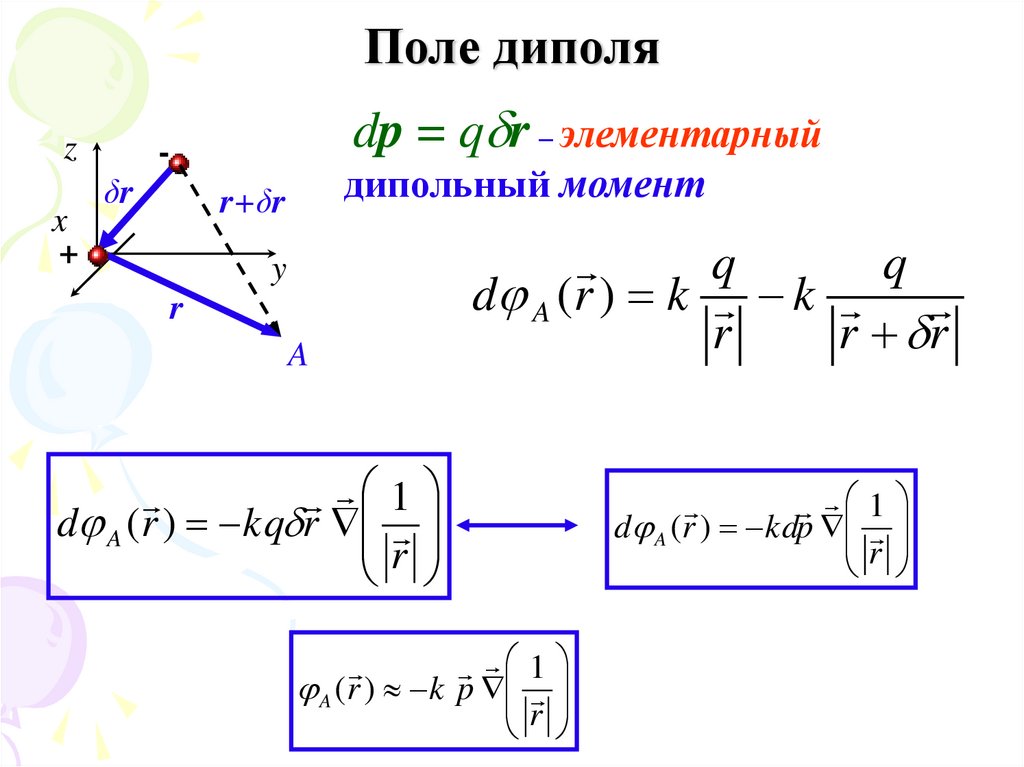
37. Поле диполя
zx
+
dp = q r – элементарный
δr
дипольный момент
r+δr
y
r
A
q
q
d A ( r ) k k
r
r r
1
d A (r ) kq r
r
1
A ( r ) k p
r
1
d A (r ) kdp
r
















 Физика
Физика








