Похожие презентации:
Электростатика. Электрические заряды
1. Электростатика
2. План лекции:
1.Электрические заряды.2.Закон Кулона.
3.Электрическое поле.
4. Вектор напряженности.
5.Теорема Остроградского-Гаусса.
6. Работа по перемещению заряда.
7. Циркуляция.
8. Потенциал.
9. Связь между потенциалом и напряженностью.
3. Закон сохранения электрических зарядов
Опытным путём (1910—1914) американский физикР.
Милликен
(1868—1953)
показал,
что
электрический заряд дискретен, т.е. заряд любого
тела составляет целое кратное от элементарного
заряда.
q ne
e =1,6∙10-19 Кл
me=9,11∙10-31 кг
4.
Алгебраическая сумма электрическихзарядов любой замкнутой системы
остаётся неизменной.
q q1 q2 q3 ... qn const
Единица электрического заряда — кулон
(Кл) — электрический заряд, проходящий
через поперечное сечение проводника
при силе тока 1 А за время 1 с.
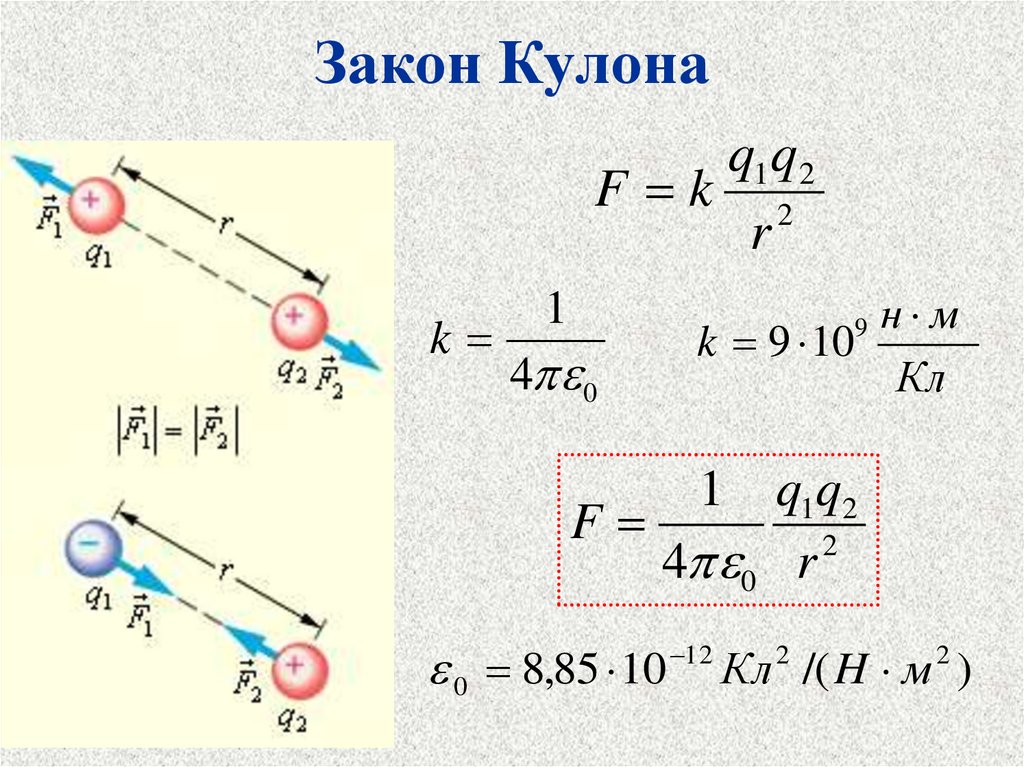
5. Закон Кулона
q1 q 2F k 2
r
k
1
4 0
н м
k 9 10
Кл
9
q1q2
F
2
4 0 r
1
0 8,85 10
12
Кл /( H м )
2
2
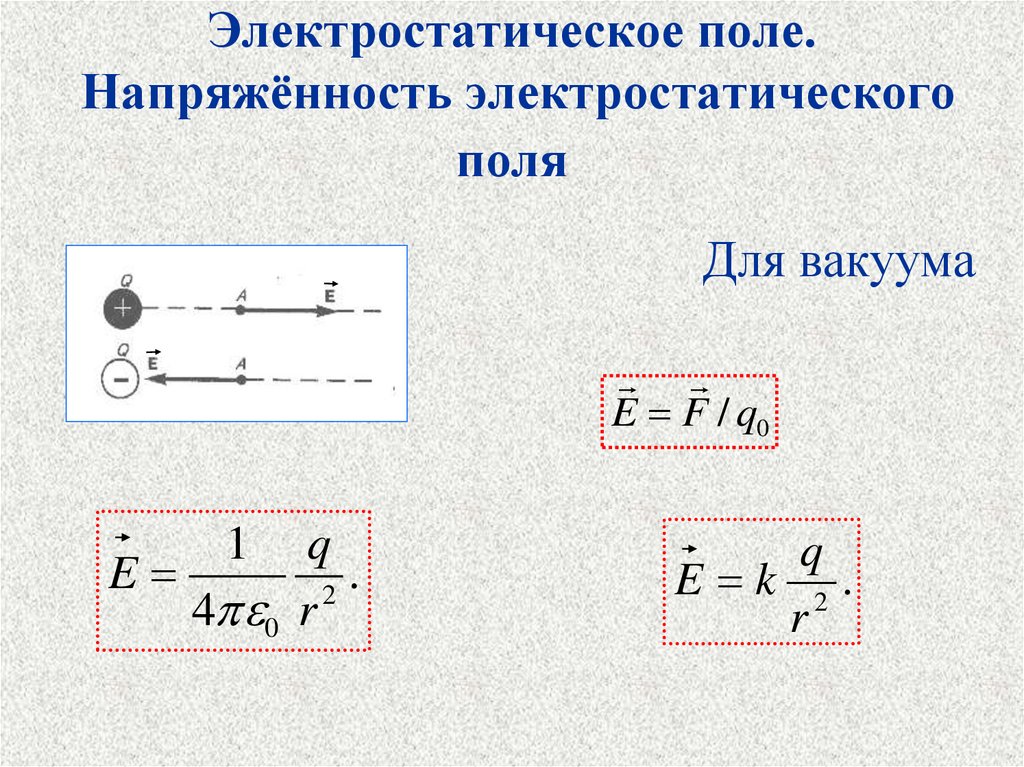
6. Электростатическое поле. Напряжённость электростатического поля
Для вакуумаE F / q0
1
q
E
.
2
4 0 r
q
E k 2.
r
7. Напряжённость электростатического поля
• Силовая характеристика поля, котораяопределяется через силу действующую на
пробный заряд в данной точке поля.
• Пробным называется единичный
положительный заряд, собственным полем
которого можно пренебречь.
8.
Электростатическое поле графически изображают спомощью силовых линий, касательные к которым
совпадают с направлением вектора — Е. Линии
напряжённости никогда не пересекаются.
9.
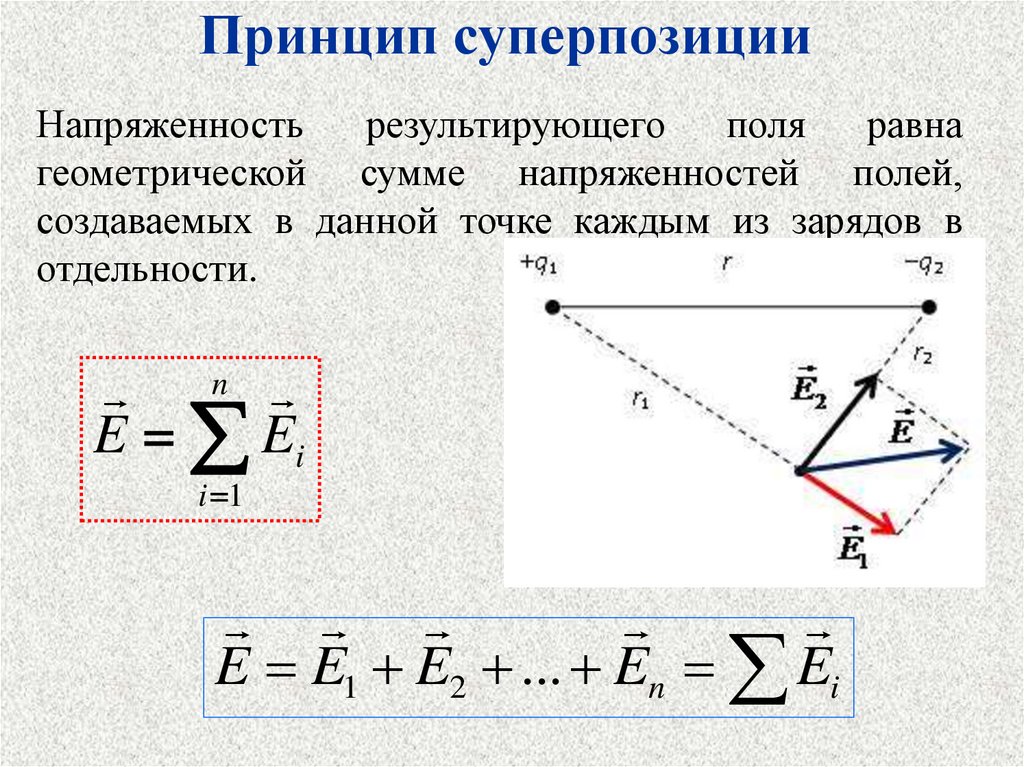
Принцип суперпозицииНапряженность
результирующего
поля
равна
геометрической сумме напряженностей полей,
создаваемых в данной точке каждым из зарядов в
отдельности.
n
E Ei
i 1
E E1 E2 ... En Ei
10.
Дипольpэ q l
-q
l
+q
p
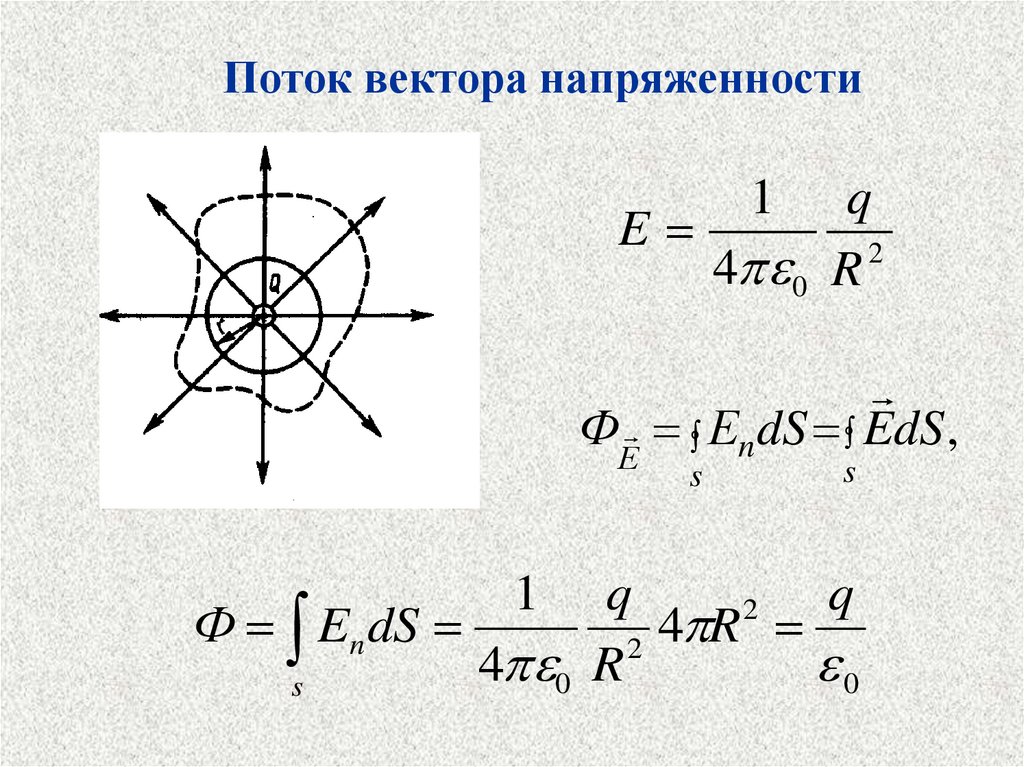
11.
Поток вектора напряженностиdФЕ EdS cos Еn dS
ФЕ Еn dS EdS ,
s
s
dS dSn
12.
Поток вектора напряженностиЕсли внутри поверхности нет зарядов, то
поток вектора Е будет равен нулю
13.
Поток вектора напряженности1
q
E
2
4 0 R
ФЕ Еn dS EdS ,
s
1
s
q
q
2
Ф En dS
4 R
2
4 0 R
0
s
14. Теорема Гаусса для электростатического поля в вакууме
Поток вектора напряженности сквозьпроизвольную замкнутую поверхность
равен алгебраической сумме заключённых внутри этой поверхности зарядов,
делённой на ε0.
1 n
E
dS
E
dS
q
n
S
S
0 i 1
15.
Теорема Гаусса для электростатическогополя в вакууме в случае одного заряда:
ФE EdS En dS q / 0
S
S
1
EdS En dS dV .
S
S
0 V
16. Применение теоремы Гаусса для расчёта некоторых электростатических полей в вакууме
17. Поле равномерно заряженной бесконечной плоскости
qS
q S
E
ФЕ 2E S
S
2 E S
0
E n / 2 0
18. Поле двух равномерно заряженных бесконечных плоскостей
E1 E 2,
2 0
E A E1 E 2
EA E1 E2 0
EС E1 E2
EС E1 E2 0
E В E1 E 2
E В E1 E 2 2
2 0 0
EВ / 0
19. Поле равномерно заряженной сферической поверхности
1Q
E
2
4 0 r
E
(r R)
20. Поле равномерно заряженного бесконечного цилиндра
1E
2 0 r
(r R)
Если r<R, то замкнутая
поверхность зарядов
не содержит, поэтому
E=0.
q
21.
Потенциал электростатическогополя
Работу
сил
электростатического
поля
определим как разность потенциальных
энергий :
qq0
1 qq0
A12
W p1 W p 2 .
4 0 r1
4 0 r2
1
Или можем записать:
A12=Wp1- Wp2=q0(φ1 - φ2).
22. Потенциал электростатического поля
Aq0
W
q0
1
q
4 0 r
23. Потенциал электростатического поля
• Определяетсячерез
работу
по
перемещению
пробного
заряда
из
бесконечности в данную точку поля (в
случае
когда
поле
создается
положительным зарядом) и наоборот из
данной точки в бесконечность (в случае
когда поле создается отрицательным
зарядом).
24.
Работу сил электростатического поляпри перемещении по замкнутому пути
определим:
A12 q0 Ed
25. Интеграл называется циркуляцией вектора напряженности Е :
( Е dl ) 0l
l
dl
E
26.
A12 q0 Edq0 1 2 q0 Ed
2
1 2 Ed
W q
1 2 Ed
U Ed
1
27. Связь между вектором Е и потенциалом φ
E gradВ декартовой системе координат:
E
i
j
k
y
z
x
Если рассматривать одномерную
задачу только по оси Х, тогда:
E
i
x
28. Электроёмкость
Cq
C
1 2
q
1
q
4 0 R
C 4 0 R
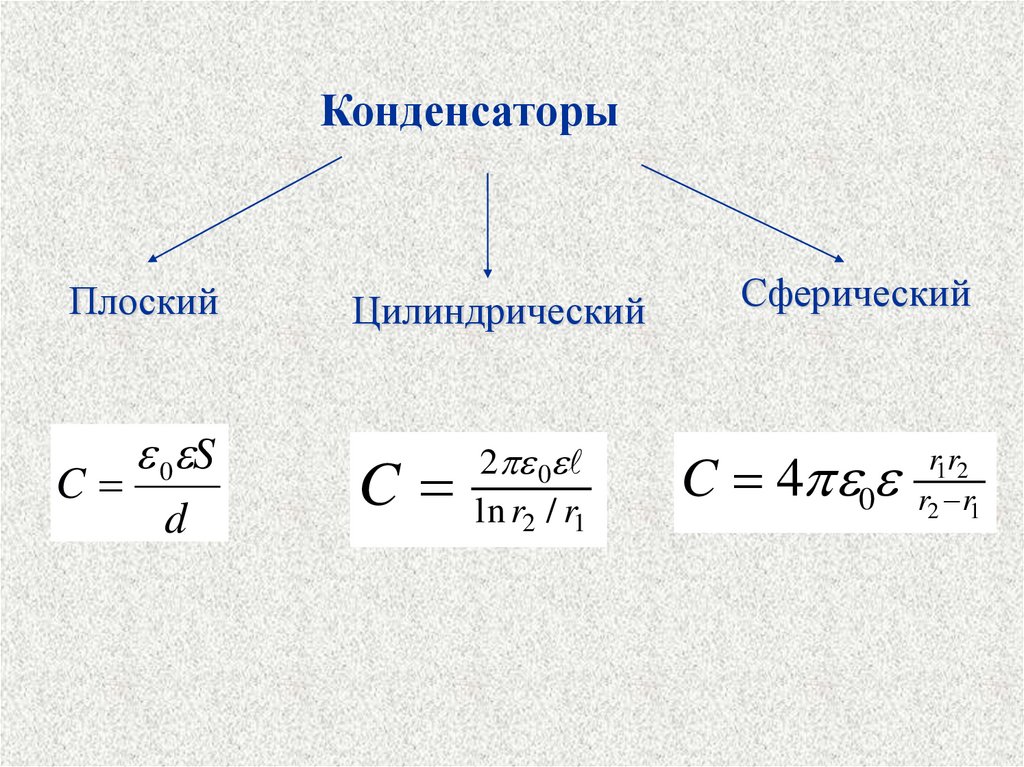
29.
КонденсаторыПлоский
C
0 S
d
Цилиндрический
C
2 0
ln r2 / r1
Сферический
C 4 0
r1r2
r2 r1
30. Поляризация диэлектриков
31.
Параллельное соединение:U const
q q1 q2 q3 ... qn
n
C C1 C 2 ... C n C i
i 1
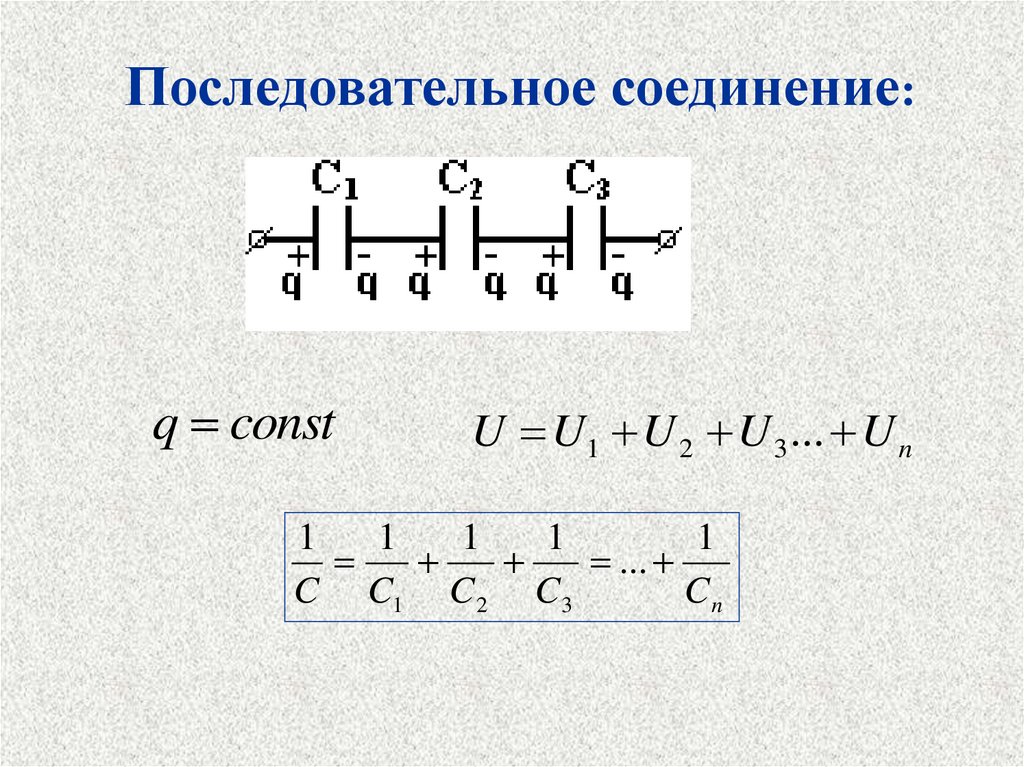
32.
Последовательное соединение:q const
U U1 U 2 U 3 ... U n
1
1
1
1
1
...
C C1 C 2 C 3
Cn
33.
Энергия электростатического поляq 2 q C 2
W
2C
2
2
q 2 qU CU 2
W
2C
2
2
q2
q2
W
x
2C 2 0 S
dW
q2
F
dx
2 0 S
34.
W0 E
2
2
Sd
0 E
2
2
V
W 0 E
ED
w
V
2
2
2





























 Физика
Физика








