Похожие презентации:
Решение систем линейных алгебраических уравнений
1. ТЕМА 2. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ Алгебраических УРАВНЕНИЙ
2.
Система m линейных уравнений с nпеременными имеет вид:
a11 x1 a12 x2 ... a1n xn b1
a x a x ... a x b
21 1 22 2
2n n
2
.........................................
am1x1 am 2 x2 ... amn xn bm
aij
bi
- коэффициенты системы,
- свободные члены.
Решением системы называется такая
совокупность значений, при подстановке которых
каждое уравнение системы обращается в верное
равенство.
3.
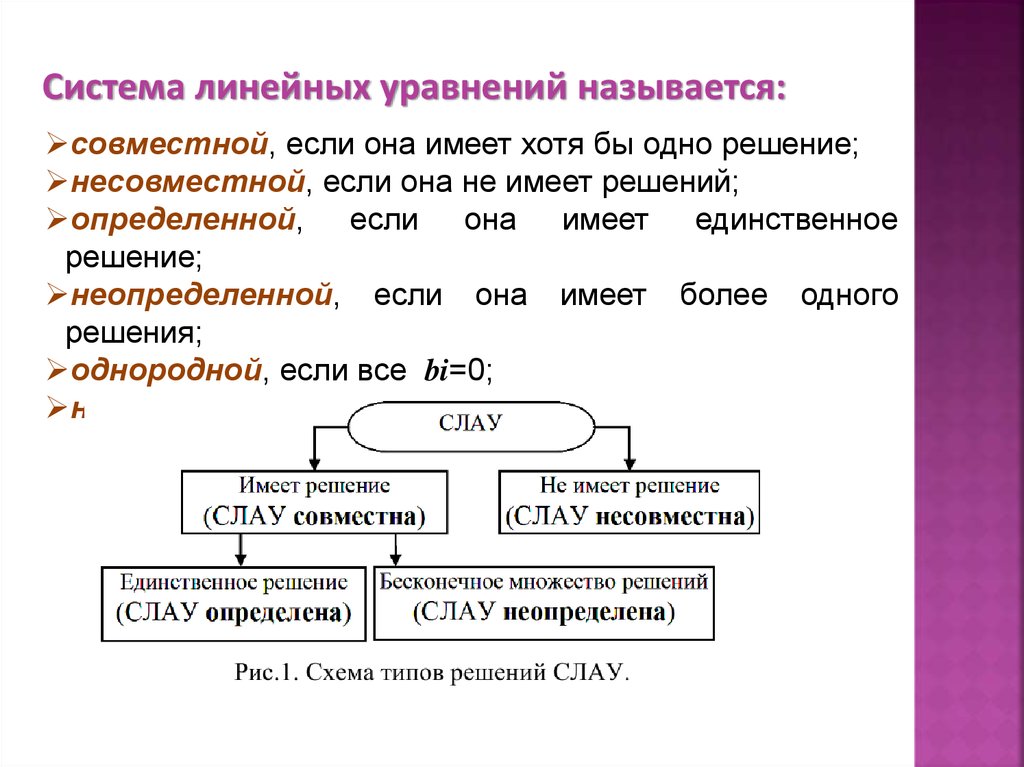
Система линейных уравнений называется:совместной, если она имеет хотя бы одно решение;
несовместной, если она не имеет решений;
определенной, если она имеет единственное
решение;
неопределенной, если она имеет более одного
решения;
однородной, если все bi=0;
неоднородной, если не все bi=0.
4.
Методы решения систем1. Метод Крамера
Рассмотрим систему n линейных уравнений
неизвестными:
a11x1 a12 x2 ... a1n xn b1
c
n
a x a x ... a x b
21 1
22 2
2n n
2
............................................
an1 x1 an 2 x2 ... ann xn bn
Теорема Крамера:
Пусть Δ - определитель матрицы системы,
Δi - определитель матрицы, получаемой из
матрицы
A
заменой
столбца коэффициентов
аij при xi столбцом свободных членов.
Тогда, если Δ ≠ 0, то система имеет единственное решение,
определяемое по формулам:
j
xj
- формула Крамера.
5.
Вспомним тему: ОпределителиОпределитель квадратной матрицы – это число,
вычисляемое по определённым правилам.
Обозначают: |А|, ΔА, detA .
Определитель 2-го
порядка:
a11 a12
2
a11 a22 a21a12
a21 a22
2 3
1 5
2 5 1 3 7
Боковая
диагональ
Главная
диагональ
6.
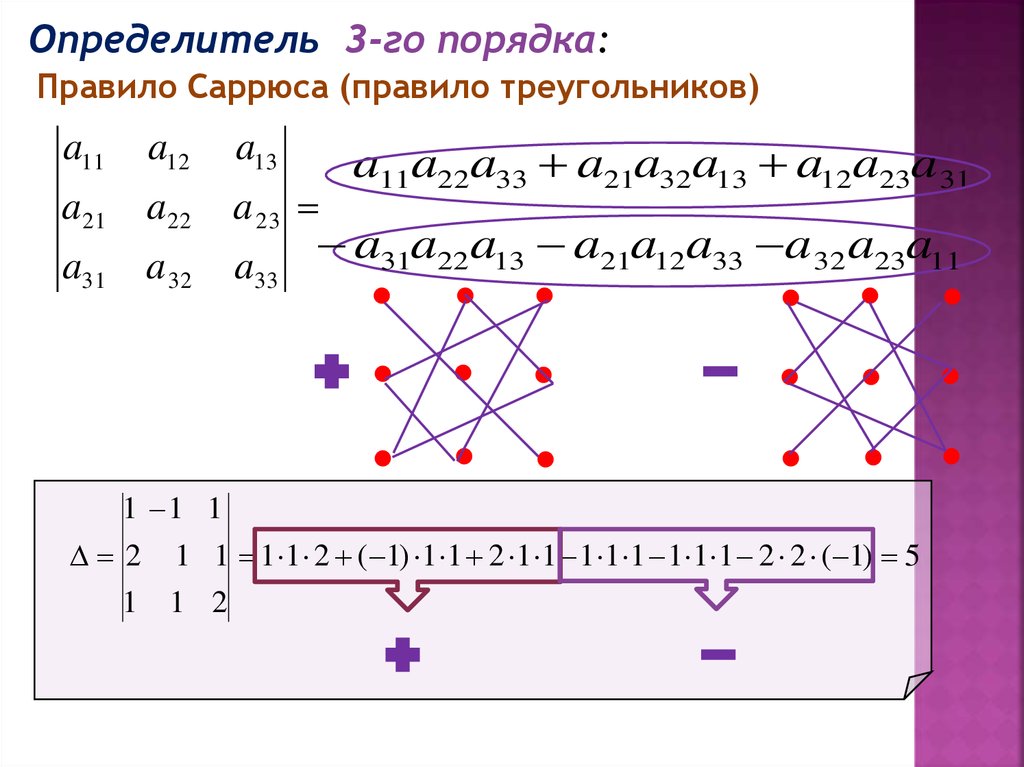
Определитель 3-го порядка:Правило Саррюса (правило треугольников)
a11
a12
a13
a21
a22
a 23
a31
a 32
a33
a11a22a33 a21a32a13 a12a23a 31
a31a22a13 a21a12a33 a 32 a23a11
1 1 1
2
1
1 1 1 1 2 ( 1) 1 1 2 1 1 1 1 1 1 1 1 2 2 ( 1) 5
1 2
7.
Вспомним тему: Алгебраические дополнения иминоры
a11 a1 j ......a1n В квадратной матрице n-го
порядка рассмотрим элемент aij.
ai1 aij ......ain Вычеркнем i-ю строку и j-ый
A
столбец, на пересечении которых
...................... стоит элемент aij. В результате
матрица
(n-1)-го
a a .. .. a получается
nn
n1 nj
порядка.
Минором Мij к элементу aij матрицы n-го порядка
называется определитель матрицы (n-1)-го порядка,
полученной из исходной матрицы вычеркиванием
строки и
i-й
j-го столбца.
Алгебраическим дополнением Аij к элементу aij
матрицы n-го порядка называется его минор, взятый со
знаком «+», если сумма i+j четная, и со знаком «-»,
если сумма нечетная: A 1 i. j M
ij
ij
8.
Пример. Решить систему методом Крамера:x1 2 x2 x3 0
2 x1 x2 3 x3 0
x x x 1
2
3
1
1 2 1
Решение. 1)Определитель матрицы системы: 2 1 3 5 0
1
2) Вычислим определители
1
0 2 1
1 0 1
1
1
3 5
1
Δ1, Δ2, Δ3 :
0 1
2 2 0
1
1
1 1
3 5
1
2
0
3 2 1 0 5.
1
1
1
1
3) Подставим полученные значения в формулу Крамера:
1
5
x1
1,
5
2
5
x2
1,
5
3 5
x3
1
5
9.
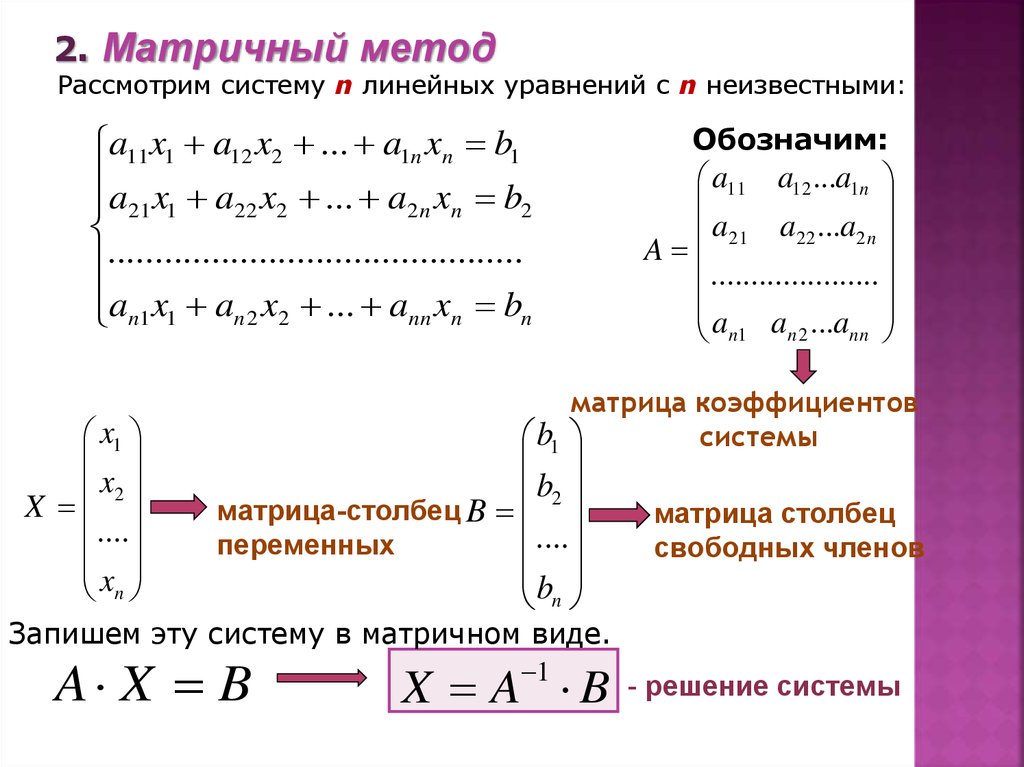
2. Матричный методРассмотрим систему n линейных уравнений c n неизвестными:
a11x1 a12 x2 ... a1n xn b1
a x a x ... a x b
21 1
22 2
2n n
2
............................................
an1 x1 an 2 x2 ... ann xn bn
x1
x2
X
....
x
n
a11 a12 ...a1n
a21 a22 ...a2 n
A
.....................
a a ...a
n1 n 2 nn
матрица коэффициентов
системы
b1
b2
матрица-столбец B
....
переменных
b
n
Запишем эту систему в матричном виде.
1
A X B
Обозначим:
X A B
матрица столбец
свободных членов
- решение системы
10.
Вспомним тему : умножение матрицПроизведением матрицы А размера m x n на матрицу
В размера n x k есть матрица С размера m x k ,
каждый элемент которой вычисляется по формуле:
n
cij ais bsj .
dim A m n
dim B n k
s 1
C A B существует
dim C m k
Вывод: число столбцов первого множителя должно
равняться числу строк второго множителя.
3
1
1 0 2
3
2
5
3 1 0 2 3
2
4 3 2
2
c11 1 ( 1) 0 5 2 2 3
11
7 2 2
c12 1 3 0 ( 2) 2 4 11
10
11.
Пример. Решить систему матричным методомx1 2 x2 x3 0
ОБОЗНАЧИМ
2 x1 x2 3 x3 0
x x x 1
2
3
1
x1
X x2
x
3
1 2 1
A 2 1 3
1 1
1
1. Вычислим определитель матрицы
1
2
det A 2 1
1
1
1
3 5 0
1
0
B 0
1
12.
3. Вычисляем обратную матрицу:3 2 0,2
0,6 0,4
1
1 ~ 1
1
A
A 3 1
1 0,6 0,2
0,2
A
5
0,2 0,4 0,6
1
2
3
4.
Проверка:
1
1
A A AA E
3 2 1 1 1
1
5 0 0
1
1
1
A A 3 1
1 2 1 1 0 5 0 E
5
5
1
2
3
1
1
2
0
0
5
13.
Вспомним тему : Обратная матрицаМатрица А является невырожденной (неособенной),
если |А|≠0, иначе матрица называется вырожденной
(особенной).
Матрица
А-1
называется
обратной
матрицей
к
квадратной матрице А, если при умножении этой
матрицы на данную как справа, так и слева получается
единичная матрица: 1
1
A A A A E
А11 А 21 А n1
1 А12 А 22 А n 2
1
A
A
А А
А
2n
nn
1n
алгебраические
дополнения к элементам
строки
записаны
в
столбец
14.
Пример. Найти матрицу обратную кматрице: A 2
1
Решение.
1. Вычислим определитель матрицы
1 1 1
А 2
1
1 5 0
1
1
2
1
1
1
1
2
1
1
определитель матрицы не равен
нулю, значит обратная матрица
существует
2. Находим алгебраические дополнения элементов
матрицы
A11 1
1 1
A12 1
2 1
1 1
1 2
A13 1
1 3
1 2
1 2
2 1
1 1
1
A21 1
2 1
1 1
1
2
1 1
3 A22 1
1 A23 1
1 1
2 2
2 3
1
1 2
1
3 A31 1
1
2
3 1
1 1
2
1
1
A32 1
1 1
A33 1
1 1
3 2
3 3
2 1
2
1
1
3
15.
2. Найдём алгебраические дополнения элементов матрицы исоставим обратную матрицу
1 3
A11 1 1 1
4
1 1
2 3
A12 1 1 2
1
1 1
2 1
1
3
A13 1
3
1 1
Обратная матрица
3. Решение системы
2 1
3 1 2 1 5
A21 1 2 1
3 A31 1
1 3
1 1
1 1
3 2 1 1 5
A22 1 2 2
2 A32 1
2 3
1 1
3 3 1 2 5
1 2
2
3
A
1
33
A23 1
1
2 1
1 1
5
4 3
1
1
A
2 5
1
5
3
1
5
4
1
1
X A B
1
5
3
x1 1, x2 1, x3
3
2
1
1.
5 0
5 1
1
5 0
5 1
5
5 1
5 1
16.
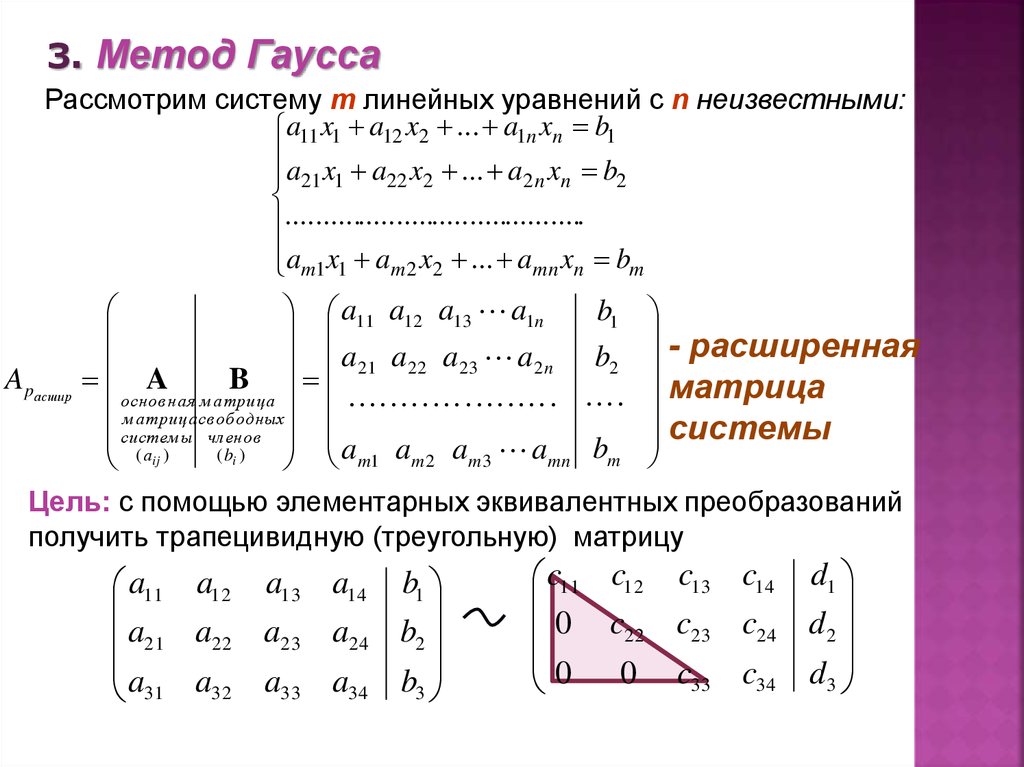
3. Метод ГауссаРассмотрим систему m линейных уравнений c n неизвестными:
a11 x1 a12 x2 ... a1n xn b1
a x a x ... a x b
21 1 22 2
2n n
2
.........................................
am1 x1 am 2 x2 ... amn xn bm
Apа сши р
a11 a12 a13 a1n
a21 a22 a23 a2 n
A
B
основная м атрица
м атрица св ободных
систем
( а ) ы чл( bенов
a a a a
)
ij
i
mn
m1 m 2 m 3
b1
- расширенная
b2
матрица
системы
bm
Цель: с помощью элементарных эквивалентных преобразований
получить трапецивидную (треугольную) матрицу
a11 a12 a13 a14 b1
a21 a22 a23 a24 b2
a
31 a32 a33 a34 b3
c11 c12 c13 c14 d1
0 c22 c23 c24 d 2
0 0 c
c
d
33
34
3
17.
Пример.Решить систему методом Гаусса
Решение:
5 x 2 y 4 z 5
2 x 3 y z 7
3 x y 2 z 3
5 2 4 5 ( 2) 1 8 6 9 ( 2)
( 3)
~
Римскими
2 3 1 7
2 3 1 7
цифрами I, II, III
~
3 1 2 3 обозначим 3 1 2
3
номера строк
1
~
8
0 19
0 4
6
9
1 8
0 19 13 25
0 23 16 30
системы
9 ( 5) 1 8 6 9 1 4 8 6 9
~ 0 1 2 0
~
13 25
0
0 1 2
0 0 5 5
0 4 3 5
3
5
6
Восстановим систему:
x 8 y 6 z 9
y 2z 0
5z 5
x 9 8 y 6 z
y 2z 2
z 1
x 1 y 2 z 1
x 9 16 6 1
y 2
z 1
18. Исследование систем линейных уравнений
Теорема Кронекера - Капелли. Для того, чтобы системалинейных алгебраических уравнений была совместна (имела
решение), необходимо и достаточно, чтобы ранг расширенной
матрицы системы равнялся рангу матрицы коэффициентов:
r ( Ap) r ( A)
r ( Ap) r ( A) , то система несовместна (не имеет
Если
решений).
r ( Ap) r ( A) n
Если
(числу неизвестных), то система
совместна и определенна (имеет единственное решение).
r ( Ap) r ( A) n
Если
, то система совместна
неопределенна (имеет бесконечное множество решений):
и
19.
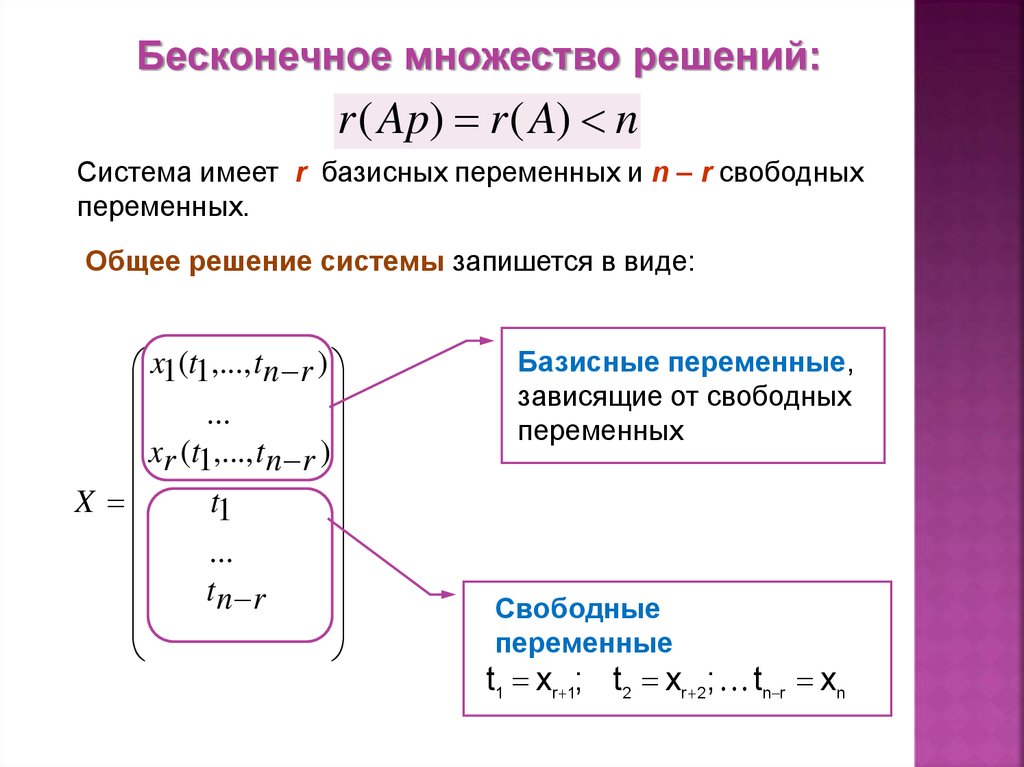
Бесконечное множество решений:r ( Ap) r ( A) n
Система имеет r базисных переменных и n – r свободных
переменных.
Общее решение системы запишется в виде:
x1(t1,..., tn r )
...
xr (t1,..., tn r )
X
t1
...
tn r
Базисные переменные,
зависящие от свободных
переменных
Свободные
переменные
t1 xr 1; t 2 xr 2; tn r xn
20. Ранг матрицы
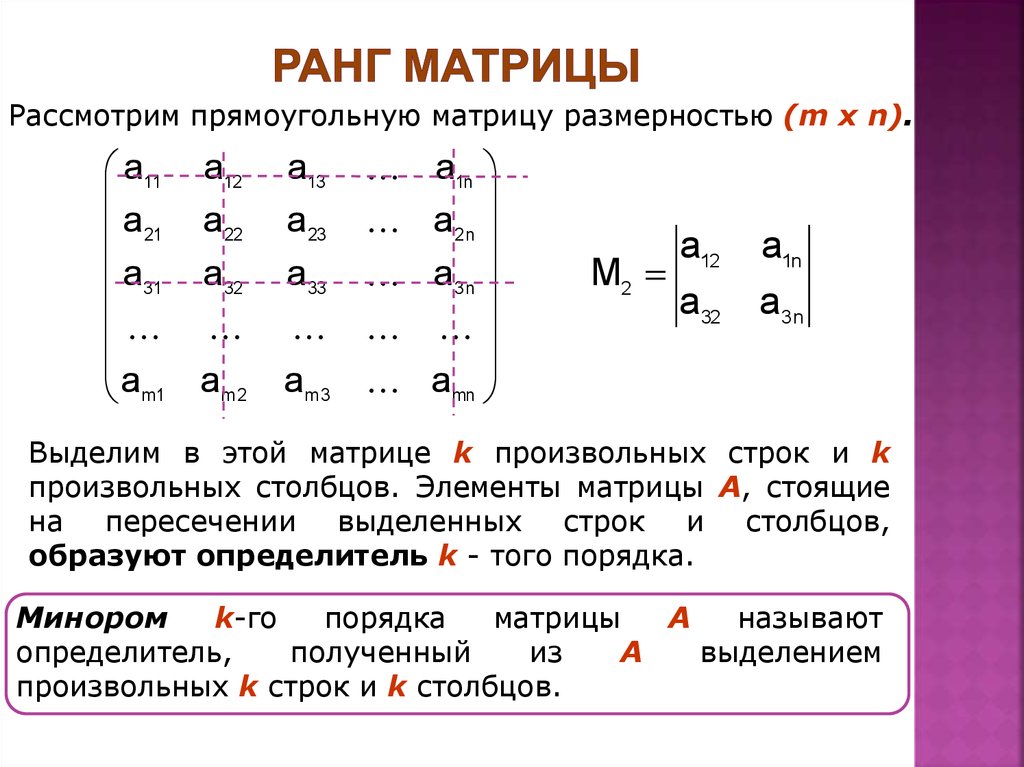
Рассмотрим прямоугольную матрицу размерностью (m x n).a11 a12
a 21 a 22
a
a 32
31
am1 am 2
a13
a 23
a 33
am3
a1n
a 2n
a3n
amn
M2
a12
a1n
a32
a3 n
Выделим в этой матрице k произвольных строк и k
произвольных столбцов. Элементы матрицы А, стоящие
на пересечении выделенных строк и столбцов,
образуют определитель k - того порядка.
Минором
k-го
порядка
матрицы
А
называют
определитель,
полученный
из
А
выделением
произвольных k строк и k столбцов.
21.
Рангом матрицы называется наибольший порядокотличного от нуля минора этой матрицы.
2 3 4 5
A 0 2 3 1
0 2 2 4
2
Матрица А имеет 4 минора 3 - его порядка,
например:
18 миноров 2 - го порядка, например:
2
3
0 2
3
4
0 2 3 20
0
4
12 миноров 1 - го порядка – сами элементы.
Наибольший порядок отличного от нуля минора
этой матрицы равен 3, поэтому: r ( A ) 3
2
2
22.
Базисным минором называется определитель, порядоккоторого равен рангу матрицы. Он может быть не
единственным.
Теорема.
Эквивалентные преобразования не меняют ранга матрицы.
Эквивалентные преобразования:
Умножение или деление элементов одного ряда на одно и то же
число, не равное нулю
Перестановка местами двух рядов
Прибавление к элементам ряда
параллельного
ряда,
умноженного
множитель
Вычеркивание нулевого ряда
элементов другого
на
произвольный
23.
Ранг матрицы равен числу ненулевых строк матрицы,приведенной к треугольному виду.
1 3 2
A 0 5 4 ~
1 7 6
1 3 2 ( 2)
~
0 5 4
0 10 8
1 3 2
0 5 4
0 0 0
r( A ) 2
Два ряда матрицы называются линейно зависимыми,
если их линейная комбинация с коэффициентами, не все
из которых равны нулю, дает нулевой ряд.
В противном случае ряды называются линейно
независимыми.
Теорема.
Ранг матрицы равен числу линейно независимых рядов
24.
Пример. Решить систему:Решение
x1
x2
x3
2 x1 2 x2 2 x3 4
x x x 0
1
2
3
3 x1 3 x2 x3 2
x1 x2 3 x3 2
2
:
2
2 2 2 4
1
1
1
2
( 3) 1 1 1
2 2 V
A p 1 1 1 0 ~ 1 1 1 0 V
0 0 2 2
3 3 1 2
~
0 0 4 4
3 3 1 2
~
1 1 3 2
0 0 4
4
1
1
3
2
x1 x2 x3
2
1 1 1
2
1 1 1
r ( Ap) r ( A) 2 совместна
0 0 2 2
0 0 - 2 2
0 0 0
0
r ( Ap) n неопределенна
0
0 0 0
2 базисных переменных, т.к. r 2 например, x1 , x3
1 свободная переменная, т.к. n r 3 2 1 например, x2 t
Восстановим систему:
x1 1 t
x
2
t
x
1
t
x
t
x
2
1
1
3
3
x2 t
2
x
2
x
1
3
3
x 1
3
25. Однородные системы линейных уравнений
a11 x1 a12 x2 a1n xn 0a x a x a x 0
21 1
22 2
2n n
am1 x1 am 2 x2 amn xn 0
Однородная система всегда имеет решение:
x1 0 x2 0 xn 0
- тривиальное решение.
Оно является единственным решением системы в случае, когда
r ( A) n
Если r ( A)
решений.
n , то система имеет бесконечное множество
26.
Решить однородную систему уравнений:x1 x2 5 x3 7 x4 0
2 x1 x2 4 x3 x4 0
3 x 2 x x 6 x 0
1
2
3
4
1 1 5 7
0 1 14 15
0 1 14 15
1 1 5 7
0 1 14 15
n r 4 2 2
1 1 5 7
1
2 1 4
3 2 1 6
~
1 1 5 7
0 1 14 15
0 0
0
0
r ( A) 2
n 4
( 2)
( 3)
~
( 1)
~
множество решений
- число свободных переменных




















 Математика
Математика








